用二分法求方程的近似解

王俊美 张超 朱柘琍

【摘 要】用二分法求方程的近似解是零点定理的应用，充分体现了方程和函数之间的联系。文章首先用案例教学法引出二分法的定义，进而解决了求方程近似解的问题，然后利用Matlab程序，在提高方程近似解精确度的同时缩短了用时，为学生日后应用该软件进行科学研究打下了良好的基础，最后对二分法求方程近似解的优缺点进行了介绍，并提出了改进方法。

【关键词】二分法;方程的近似解;零点定理;Matlab

【中图分类号】G642  【文献标识码】A  【文章编号】1671-8437（2022）12-0001-03

在解决实际问题时常常需要求一个方程的实根，但除了一些简单的方程，大部分方程都很难求出准确解，因此求方程的近似解在数学应用上具有重要意义[1]。本文用案例法介紹了求方程近似解的方法——二分法，同时用Matlab程序可以求出方程不同精确度的近似解，与其他方法相比缩短了求方程近似解的时间。

1   学情分析

大一学生已经学习了函数知识，理解了函数零点和方程根的关系，初步掌握了函数与方程的转化思想。但是对于求函数零点，学生只是比较熟悉求二次函数的零点，求高次方程和超越方程对应函数零点却有一定困难。

2   课程设计

本文首先将天平测量假币案例作为教学素材，以期激发学生的学习兴趣，突显学生在课堂上的主体地位，充分发挥学生的主观能动性。同时将教材中的概念和理论知识与生活实际相结合，做到学以致用，通过具体实例的探究，归纳概括所发现的结论或规律，体会从具体到一般的认知过程。其次利用现代信息化教学模式，在高等数学教学中适当地引入Matlab软件，利用Matlab的强大计算功能提高课堂教学效率，为学生日后应用该软件进行科学研究打下良好的基础。最后对二分法求方程近似解的优缺点进行介绍，并针对缺点提出了改进办法。

本课程设计在第五届（2019）全国高校数学微课程教学设计竞赛中获得全国二等奖、华东赛区特等奖、山东省特等奖。

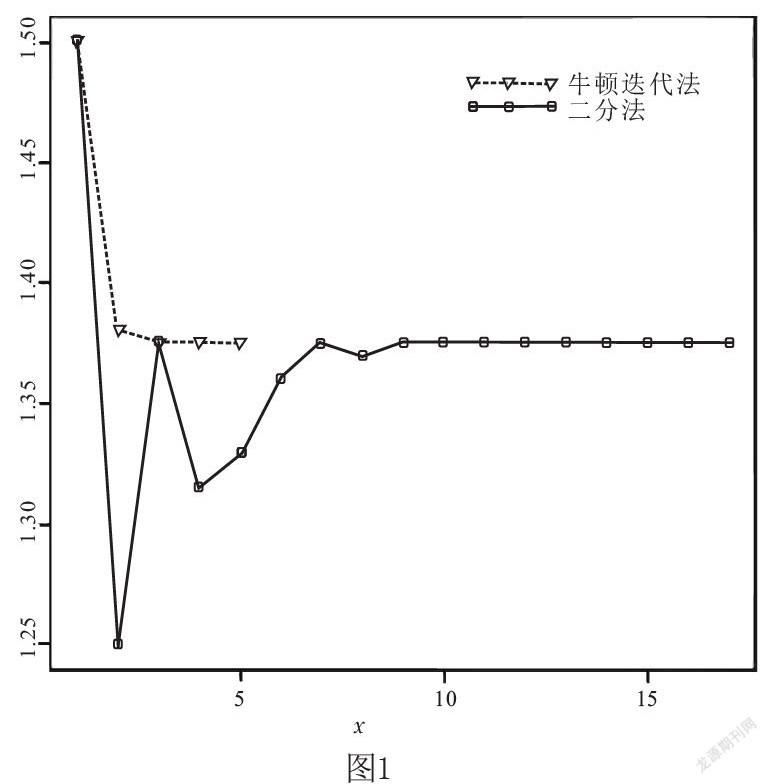
针对收敛速度慢的缺点，可采取的改进方法是将二分法和牛顿切线法结合。

整个教学设计以问题为教学出发点，以教师为主导，学生为主体，设计情境激发学生的学习动机，将二分法求方程的近似解的方法与现实生活中案例联系起来，让学生体会数学方法来源于现实生活，又可以解决生活中的问题，培养了学生利用从特殊到一般，再由一般到特殊的思维方式解决问题的能力。同时，学生体会到了Matlab软件的强大运算功能，为后续课程中Matlab的应用奠定了基础[5]。

【参考文献】

[1]王希超，李全忠，刘长文.用夹逼法求方程的近似解[J].山东农业大学学报（自然科学版），2003（4）.

[2]欧小雪.“用二分法求方程的近似解”教学设计[J].科学教育家，2008（1）.

[3]肖息贵，唐生福，石宝.用二分法求方程近似解的教学思考[J].桂林师范高等专科学校学报，2008（9）.

[4]田学飞.利用matlab解决二分法求方程的近似解问题[J].商情（科学教育家），2008（2）.

[5]雷勇.《用二分法求方程的近似解》教学设计[J].邵通师范高等专科学校学报，2011（1）.

【作者简介】

王俊美（1977～），女，汉族，山东德州人，硕士，讲师。研究方向：高等数学教学与研究。

朱柘琍（1978～），女，汉族，山东泰安人，硕士，副教授。研究方向：高等数学教学与研究。

【通讯作者】

张超（1979～），男，汉族，山东新泰人，硕士，副教授。研究方向：高等数学教学与研究、农业大数据挖掘、物联网与精准农业。