基于细观模拟的碾压混凝土尺寸效应律研究

魏培勇， 张社荣， 王 超， 王枭华 ， 和孙文

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350;2.天津大学建筑工程学院，天津 300350;3.中国水利水电第十四工程局有限公司，昆明 650041)

试验和理论研究表明，混凝土在压缩、剪切、拉伸等静态荷载作用下呈现出明显的尺寸效应。在准静态力学试验中，小尺寸试件通常可以承受更大的破坏荷载。针对混凝土材料层次的尺寸效应理论主要有以下三类：①统计尺寸效应理论[1]；②长裂缝导致的应力重分布和断裂能量释放理论[2]；③裂纹多重分形理论[3]。

作为一种率相关材料，高应变率荷载作用下，混凝土材料的力学特性呈现明显的应变率效应。换言之，相较于静态力学特性，动态荷载下混凝土强度、断裂能等力学特性均有所提高。研究表明，混凝土材料的应变率效应主要由横向约束作用[4]、裂纹扩展作用[5]、Stefan效应引起[6]。其中，裂纹扩展作用是指在高速冲击作用下，微裂纹可能穿过粗骨料而不是沿着界面过渡区(ITZ)等较薄弱区域扩展；Stefan效应，也称为粘滞效应，即动力荷载作用下混凝土内部微缺陷中自由水会制约其变形。除了上述材料特性外，横向惯性和断面摩擦等引起的结构效应也会影响应变率效应。同时，试验和理论研究表明，动力冲击荷载作用下，混凝土的动态尺寸效应与静态尺寸效应之间存在显著差异，例如：在相同应变率荷载作用下，动态强度随试件尺寸增加呈现增长趋势，同时大尺寸试件应变率效应更显著。然而，目前关于混凝土类材料动态尺寸效应方面研究较少，制约了室内小尺寸结构试验成果在全尺寸结构抗冲击设计中应用。

作为一种特殊混凝土材料，碾压混凝土具有低水泥用量、低水化热、零坍落度、分层碾压成型等特点，已被广泛应用于水工大坝建设中。关于碾压混凝土抗冻性[21]、温度场[22]、抗渗性[23]、层面抗剪性能[24]、动态压缩性能[25]研究表明，独特的材料组分和施工方式造成了碾压混凝土和常态混凝土的力学性能不尽相同。同时，碾压混凝土成型质量受碾压遍数、振动频率影响，导致试验结果呈现较大离散性。综上可知，有必要通过细观数值模拟对组分独特的碾压混凝土材料动态尺寸效应进行研究，避免室内试验对结果离散性的影响，为全尺寸结构抗爆防护研究提供一定依据。

为深入研究碾压混凝土静动态荷载下尺寸效应，本文将碾压混凝土视为砂浆、粗骨料和ITZ组成的三相复合材料，同时粗骨料简化为球体，建立了五种不同直径(D=50,75,100,125,150 mm)的圆柱体三维随机骨料模型，并对比数值模拟和现有试验结果验证了细观模型的有效性。通过不同应变率作用下的碾压混凝土压缩试验模拟，分析了应变率和试件尺寸对碾压混凝土动态压缩性能的影响，在混凝土类材料尺寸效应律的基础上，提出了碾压混凝土静动态压缩尺寸效应公式。

1 细观模型与验证

1.1 3D细观模型建立

为反映混凝土内部的非均质性，本研究中将碾压混凝土看作骨料粒径、砂浆基质以及二者之间的界面过渡区(interfacial transition zone, ITZ)组成的三相复合材料。研究表明，粗骨料形状对混凝土材料动态抗压强度的影响并不显著。为简化计算，本研究中将骨料形状简化为球体，粗骨料粒径范围为5～20 mm,体积分数为60%。采用Monte-Carlo方法随机生成骨料坐标及半径，并确保各粒径骨料数量符合Fuller级配曲线，最后采用“背景网格投影”[26-27]的方法将均一化网格划分为骨料、砂浆、ITZ三种材料。最终建立的五种不同尺寸的碾压混凝土圆柱试件细观模型，试件长径比L/D为0.5，模型直径分别为50、75、100、125、150 mm。需要说明的是，由于层面结构对碾压混凝土动态抗压强度影响并不显著，建模中忽略层面结构的影响。

由于数值计算结果的收敛性受网格尺寸的影响，分别选取2.0 mm、1.0 mm、0.5 mm三种密度进行试件网格剖分和有限元试算。由图1可知，网格密度0.5 mm和1.0 mm时，透射波的应力时程曲线几乎重合，说明数值模拟结果已经收敛，同时为减少计算量，本文中采用1.0 mm作为试件网格划分密度，图2给出了碾压混凝土细观有限元模型和数值模拟示意图。其中，压杆横截面始终与试件截面相匹配。

图1 不同网格剖分密度下试算结果

图2 碾压混凝土细观模型及数值仿真示意图

1.2 材料本构模型及参数选取

HJC(Holmquist-Johnson-Cook)模型是针对混凝土类材料提出的一种率相关损伤型本构模型，广泛应用于混凝土高速冲击、爆炸等动态荷载作用下的力学响应。HJC本构模型主要包含屈服面方程、损伤演化方程和状态方程三部分，如图2所示。

其中，强度方程可以被描述为

(1)

参考文献[28-29]中对花岗岩材料动态力学特性及HJC本构参数的研究，确定了骨料材料参数取值；砂浆参数则参考前期[30]对碾压混凝土HJC本构修正研究进行取值；研究表明，可将ITZ视为孔隙率略大的砂浆基质，其材料参数(密度、抗拉及抗压强度、弹性模量等)会有一定程度的弱化[31]。通过试算，最终确定砂浆、骨料和ITZ参数分别如表1～表3所示，计算时采用mm-g-μs单位制。

此外，入射杆、透射杆和子弹均采用线弹性钢本构模型(*MAT_ELASTIC)，弹性模量取200 GPa。压力杆与试件间采用侵蚀面面自动接触，接触算法采用罚函数算法，罚因子取2.0[32]。

表1 砂浆HJC模型参数

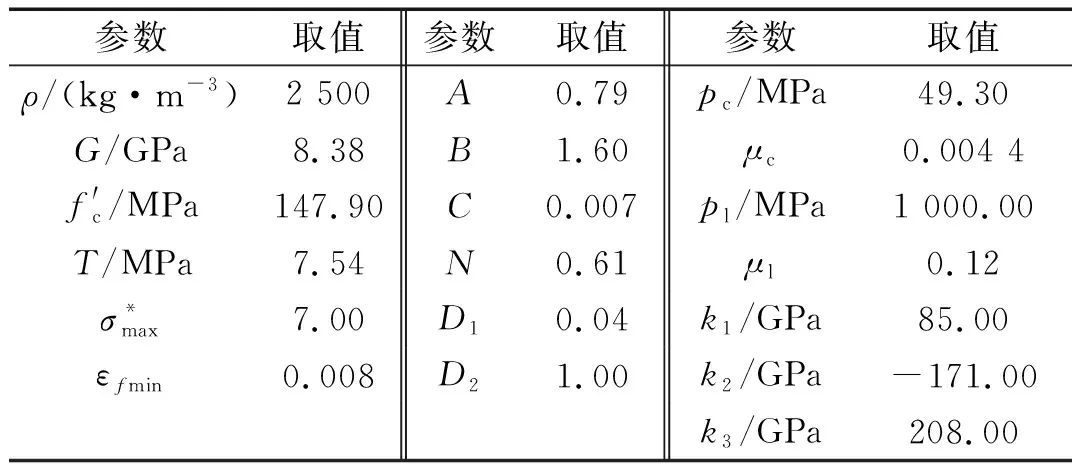
表2 骨料HJC模型参数

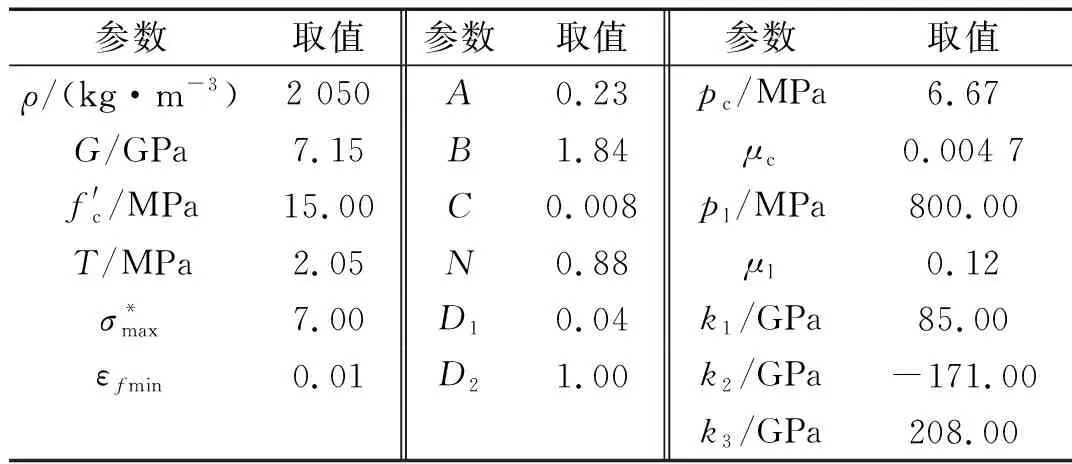
表3 界面过渡层HJC模型参数

1.3 模型有效性验证

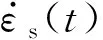
(2)

(3)

(4)

式中:A0，c0，E0分别为压力杆的横截面积、波速和弹性模量；As和ls分别为试件的横截面积和长度；εi(t)，εr(t)和εt(t)分别为入射杆上采集到的入射波、反射波和透射杆上采集到的透射波。

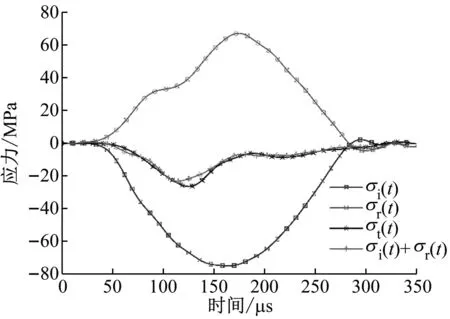
取入射杆和透射杆中部单元(图2中测点A与测点B)作为数据采集点，以获取杆中轴向应力波形并计算试件应力应变曲线。图3(a)给出了典型应力时程曲线及应力平衡验证结果，由图可知，入射应力波与透射应力波之和(σi(t)+σr(t))与投射应力波σt(t)波形较为接近，表明数值模拟中试件两端可以达到应力平衡[33-35]。

(a)

图3(b)给出了三种不同应变率下碾压混凝土(D=50 mm)数值仿真结果与文献中SHPB室内试验数据的对比结果。由图3可知，数值仿真得到的应力应变曲线动态弹性模量更高，这种现象可能是由于数值模拟中未考虑碾压混凝土内部微观孔隙的受压密实过程，同时数值模拟中试件两端面不存在平行度公差，而平行度公差在实际试验中必然存在，这会导致试验得到的弹性模量较低。另一方面，试验得到的应力应变曲线应力峰值附近存在变化相对缓和的“平台”，而数值模拟结果峰值更明显且卸载阶段曲线更陡，这种现象主要是由于数值模拟中单元失效即被删除，无法模拟实际试验中的孔洞被压实紧密的过程。除此之外，在SHPB试验和模拟计算中，碾压混凝土试样表现出的应力应变行为基本一致。因此，本文使用的碾压混凝土细观模型可有效模拟SHPB试验并反映材料的动态压缩性能。

2 碾压混凝土动态压缩力学行为

为研究碾压混凝土的应变率效应及动态压缩尺寸效应，基于上述SHPB试验模型，对5种不同尺寸(长径比L/D=0.5，试样直径D(50 mm、75 mm、100 mm、125 mm、150 mm)碾压混凝土试件在不同应变率下力学行为进行了数值仿真分析，并与碾压混凝土室内SHPB试验结果[36-37]进行对比验证。需要说明的是，除试件尺寸外，碾压混凝土试件粗骨料含量、粗骨料最大粒径、混凝土强度等级等因素均保持一致。

2.1 碾压混凝土破坏模式

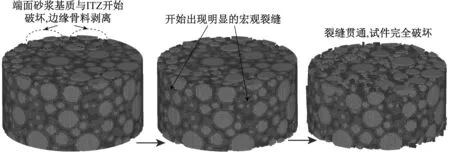
(a)

2.2 应力应变关系

图5 不同应变率下碾压混凝土试件应力应变关系曲线

3 动态抗压强度尺寸效应分析

3.1 动态抗压强度与试件尺寸间关系

动态增强因子(dynamic increase factor,DIF)通常被用于表征动态荷载下材料强度增强现象。表4及图6(b)中给出了数值模拟得到的DIF值与碾压混凝土试验结果以及相关文献中经验公式[38-42]的对比。需要注意的是，文献[37]中经过分层碾压成型、钻孔取芯等流程最终得到碾压混凝土试件，其动态抗压强度试验结果具有较大的离散性，表4中给出的试验结果为其平均值。由表4可知，对于D75试件，高应变率下试验得到DIF平均值大于数值仿真结果；而对于D50试件则呈现出相反趋势。由图6(b)可知，尽管室内SHPB试验结果离散性较大，数值仿真得到的DIF数据点与试验结果较为吻合，同时均落在常态混凝土尺寸效应经验公式范围内。

表4 不同应变率下数值模拟与SHPB试验DIF值对比

(a)

3.2 Bazant尺寸效应律修正

基于断裂力学理论的Bazant尺寸效应律[43]也被广泛应用于混凝土材料的准静态尺寸效应描述中，其表达式如式(5)所示。同时金浏等通过数值模拟对常态混凝土动态压缩和拉伸强度的Bazant尺寸效应律参数进行了修正。

(5)

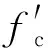
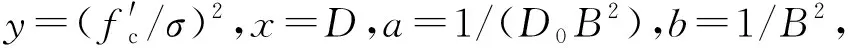
y=a*x+b

(6)

对数值仿真结果进行回归分析，得到不同应变率下a和b的数值如表5所示。

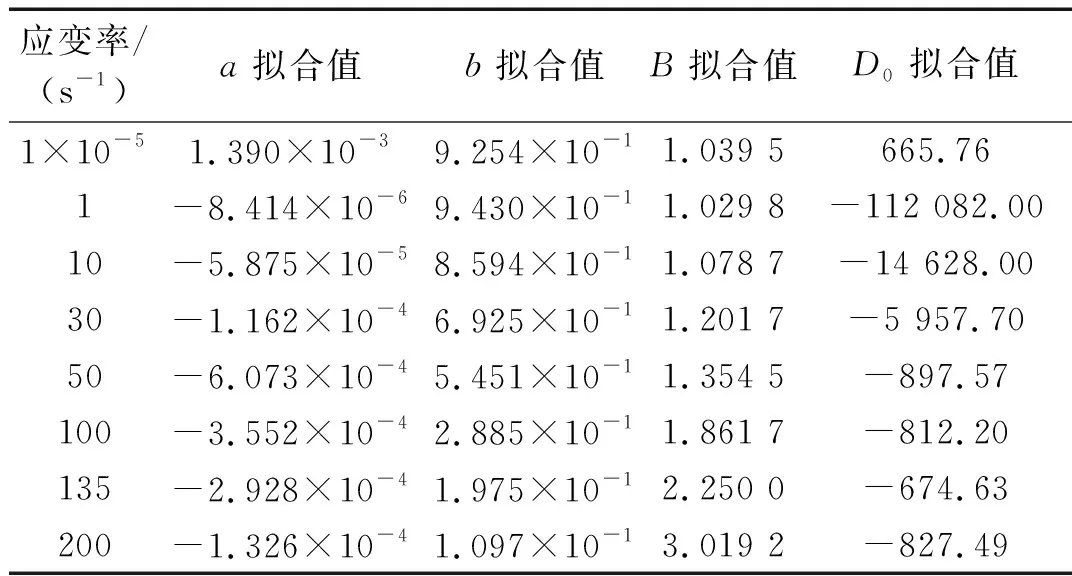
表5 不同应变率下Bazant尺寸效应公式参数拟合结果

(7)

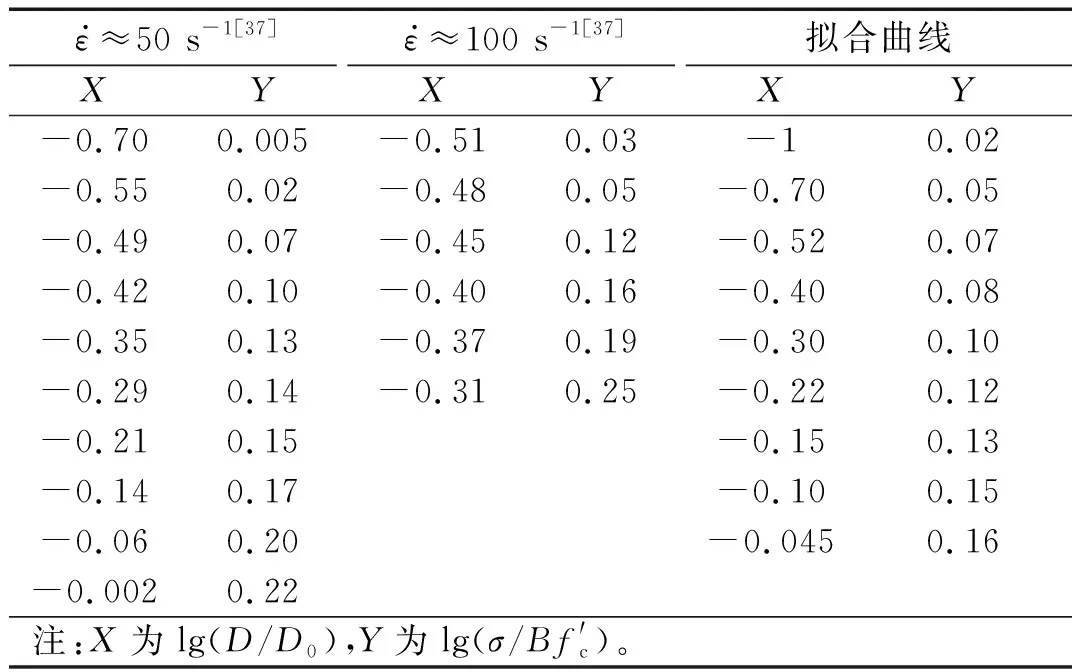
表6 Bazant尺寸效应律拟合及与试验结果对比

(a)

4 结 论

基于细观建模方法和HJC本构模型，本文建立了碾压混凝土细观数值模型，研究了静动态荷载作用下圆柱形碾压混凝土试件的尺寸效应，提出了适用于碾压混凝土材料的尺寸效应律。主要结论如下：

(1) 动态荷载下，碾压混凝土呈现出与准静态荷载下相反的尺寸效应行为。准静态荷载下，碾压混凝土抗压强度随试件尺寸增长而减弱；动态荷载下，其抗压强度随试件尺寸增长而增强，且抗压强度增量随应变率增长而增长。

(2) 与常态混凝土研究成果类似，存在一临界应变率，在此应变率附近，试件尺寸对碾压混凝土抗压强度影响可以忽略。

(3) 基于Bazant静态尺寸效应律，验证准静态荷载下数值仿真结果的合理性；同时基于数值模拟结果，提出了碾压混凝土动态尺寸效应律。经对比，SHPB试验数据与本文提出的碾压混凝土尺寸效应律较为吻合，进一步验证了数值模拟方法的合理性。

(4) 需要注意的是，本文中细观模型没有考虑碾压混凝土层面和碾压混凝土内部孔隙的影响，因此后续研究中应将内部孔隙结构引入到细观模型中，探究孔隙结构及薄弱层面对碾压混凝土性能的影响。