基于电压的压电悬臂梁剩余寿命预测

吴兴意， 刘文光， 胡剑波， 方孟翔， 高铭阳

(南昌航空大学 航空制造工程学院，南昌 330063)

压电悬臂梁广泛应用于能量收集器设计，由于其结构简单、能量转化效率高和易于集成化等优点，备受研究者的关注[1-3]。

近年来，研究者围绕压电悬臂梁式振动能量收集器的发电效率展开了大量的研究。王青萍建立了压电悬臂梁式能量收集器的输出电压与激励位移和激励力的关系[4]，鲁庆庆研究了多模态压电能量收集器的电压输出值与激振加速度的关系[5]，Uddin等[6]研究了悬臂梁末端质量块的重量与能量收集器输出电压的关系，Mohamed等[7]应用优化压电悬臂梁几何尺寸的方式提出了一种压电悬臂梁式能量收集器的设计方法，陈文科等[8]设计了一种梯形悬臂梁式压电能量收集器以提高能量收集器的发电效率，Wang等[9]研究了不同形状对压电悬臂梁发电性能的影响，陈仲生等[10]研究了外加非线性磁力对压电能量收集器输出电压的影响，杨倩倩等[11]研究了重力对压电悬臂梁发电效率的影响。

研究表明，增大外部激励或优化压电结构是提高能量收集器发电效率的有效途径。然而，由于压电悬臂梁式能量收集器在工作时需持续承受振动载荷，很容易导致疲劳裂纹、疲劳脱落等损伤，进而影响压电悬臂梁的使用性能[12-13]。而且提高能量收集器的发电效率，意味着要增大压电悬臂梁的振动响应，势必导致压电悬臂梁的内部应变随之增加，严重缩短压电悬臂梁的剩余寿命。针对悬臂梁的振动疲劳行为，王锦丽等[14-15]研究了激励频率对悬臂梁振动疲劳特性的影响，张淼等[16-17]分析了梁的尺寸和激励位移对压电悬臂梁疲劳寿命的影响，Avvari等[18]研究了激励幅值对压电悬臂梁疲劳寿命的影响，陈林雄等[19]研究了振幅对压电悬臂梁疲劳寿命的影响，Peddigari等[20]研究了基体对压电悬臂梁振动疲劳寿命的影响。

尽管研究者在压电悬臂梁式振动能量收集器的能量转换效率和振动疲劳分析方面做了很多工作，但鲜有研究者建立压电悬臂梁共振频率、剩余寿命与发电电压的关系。本工作以压电悬臂梁为对象，测试了压电悬臂梁的共振频率、发电电压和振动循环次数，以发电电压为识别指针，提出了一种基于电压的压电悬臂梁剩余寿命预测模型，实现了压电悬臂梁的剩余寿命预测。

1 试验方法

1.1 试验件

以能量收集器用压电悬臂梁为试验件，如图1所示。试验件由两块矩形压电陶瓷薄片和矩形铜薄片组成。铜薄片基体的几何尺寸为80 mm×33 mm×0.2 mm，压电陶瓷薄片的几何尺寸为60 mm×31 mm×0.2 mm。压电陶瓷为PZT-5a，极化方向如图1(a)所示。利用导线A连接上、下表面实现两片压电陶瓷片的并联，利用导线B、导线C导出试验件振动致电信号，如图1(b)所示。

(a) 几何形状

1.2 试验方法

以图2所示的试验系统开展试验。试验系统包括旋磁激振装置、夹具、示波器以及数码电子显微镜等。旋磁激振装置的工作原理是在试验件的自由一端粘贴磁铁，通过调速电机驱动附加磁铁的圆盘转动，当圆盘上磁铁与试验件上磁铁相遇时将产生磁力，试验件在磁力驱动下产生受迫振动，见图2(a)。

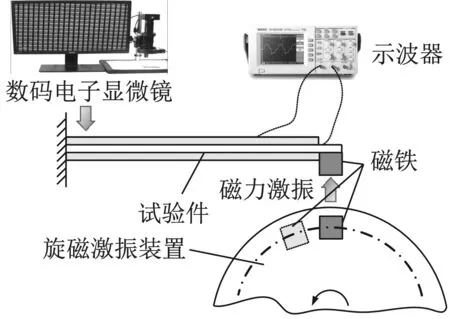
(a) 试验系统示意图

试验前，通过压块将试验件一端固定，形成悬臂梁结构。利用示波器记录试验件的发电电压，通过数码电子显微镜监测试验件的损伤。开展振动疲劳预试验，确定试验件初始共振频率与共振状态下的发电电压值。试验发现，试验件没有出现明显损伤时，其共振频率随振动加载逐渐降低；但试验件上压电陶瓷层出现裂纹后，压电陶瓷层很快会出现断裂、脱落等严重损伤。试验以观测到可见裂纹(图3)为准则认定试验件失效。

图3 损伤试验件实物图

因为试验件的总体刚度会随着试验件损伤的累积而出现一定程度的损失，试验件的共振频率也会随之下降，使得试验件远离共振，导致其振幅和发电电压显著降低。由于试验件共振频率变化受诸多因素的影响，为简化分析，试验将试验件的发电电压达最大时所对应的激励频率记录为此刻试验件的共振频率。所以，试验中结合试验件的振幅变化和发电电压幅值调节激励频率，频带激励旨在调节旋磁激励频率使试验件发电电压最大或者振幅最大。本试验通过手动调节电机转速调节旋磁激振频率，保证试验件接近共振频带激励状态以加速试验件损伤。

1.3 试验结果

将试验件分别编号为A、B和C。试验测试了三个试验件的发电电压、共振频率和循环加载次数。图4描述了循环加载次数与试验件共振频率的关系，图5描述了循环加载次数与试验件发电电压的关系，图6描述了共振频率与试验件发电电压的关系。

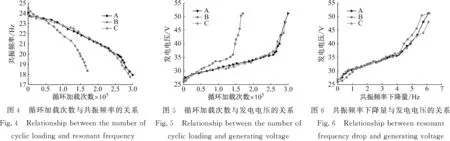
循环加载次数的计算式为

Nj=nj×m×tj+Nj-1

(1)

式中：Nj、Nj-1分别表示第j阶段、第j-1阶段对应的循环加载次数;nj表示第j阶段对应电机转速;m表示旋磁激振装置上的磁铁数量;tj表示第j阶段所经历的时间。

结果表明，随着循环加载次数的累加，试验件的共振频率逐渐下降，而且下降率逐渐增大。随着共振频率的下降，共振频带激励下，试验件的振动响应不断增大，其宏观表征之一是试验件的振幅逐渐增大，从而导致共振状态下的发电电压呈现上升趋势，且在损伤达到一定程度后，其上升速率突然增大。当试验件的压电陶瓷层出现疲劳裂纹或松脱时，试验件A的共振频率下降6.1 Hz，发电电压上升24.4 V；试验件B的共振频率下降6.15 Hz，发电电压上升25.2 V；试验件C的共振频率下降6.1 Hz，发电电压上升21.2 V。

2 基于电压的剩余寿命预测

2.1 基于电压的损伤率模型

假设f0表示试验件的初始共振频率，fi表示某一损伤阶段的共振频率，Ni表示对应损伤阶段的循环加载次数，Nk表示试验件失效时经受的循环加载次数。图7描述了试验件的疲劳寿命比Ni/Nk与共振频率比fi/f0的关系。

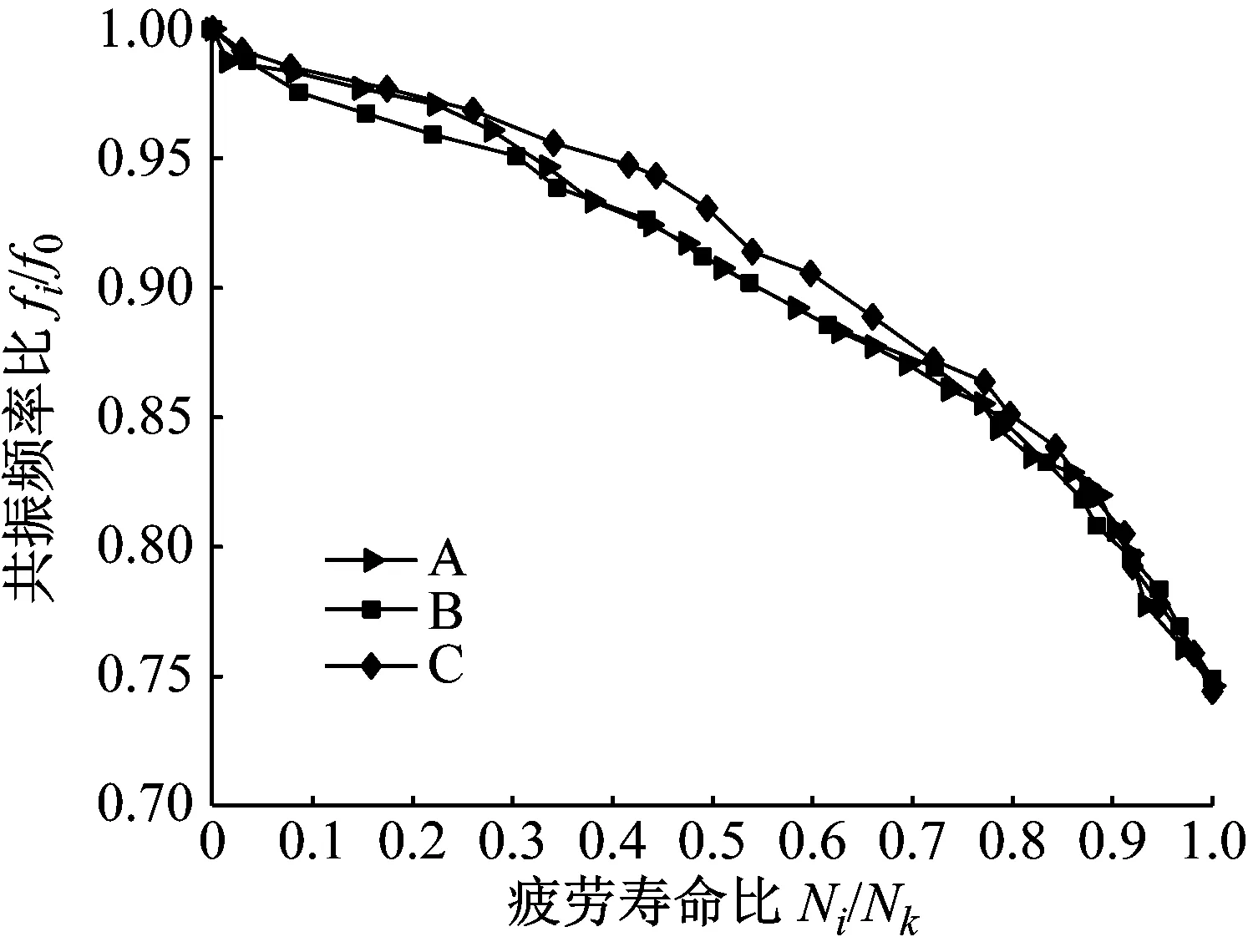
图7 疲劳寿命比与共振频率比的关系

结果表明，试验件失效时的共振频率分别下降25.36%、25.10%、25.58%。为此，本文将试验件共振频率下降25%时定义为完全失效状态。根据线性损伤累积理论，损伤程度为0时，试验件共振频率无变化；损伤程度为1时共振频率下降25%，将试验件的损伤率Di定义为

(2)

图6结果表明，随着试验件的损伤累积，其发电电压随着共振频率的变化而变化，且二者之间存在一定的内在联系。而另一方面，根据上述所建立的共振频率与损伤率的关系，可进一步建立发电电压与损伤率的关系。为了更好地理解此关系，将电压上升率λi定义为

(3)

式中:Vi表示不同损伤阶段试验件的发电电压;V0表示试验件初始状态时的发电电压。

图8分析了电压上升率λi和损伤率Di的关系。为了建立二者间明确的数学关系，基于最小二乘法可拟合出电压上升率λi和损伤率Di的多项式数学模型

(4)

根据损伤指针的定义，初始状态试验件的损伤率D0为0，失效状态的损伤率Dk为1。相对应，无损伤时，试验件的电压上升率λ0为0；失效时电压上升率λk为某定值。因此，可借助电压上升率来判断试验件的损伤程度。

图8 电压上升率与损伤率的关系

2.2 基于电压的剩余寿命预测

图9描述了试验件疲劳寿命比Ni/Nk与损伤率Di的关系。基于最小二乘法可拟合出疲劳寿命比与损伤率的幂函数关系式

Di=(Ni/Nk)1.744

(5)

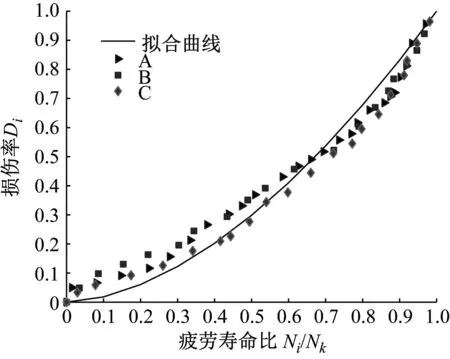
图9 疲劳寿命比与损伤率的关系

通过式(5)，可得到压电悬臂梁的剩余寿命预测数学模型

(6)

基于式(6)，在已知当前累计循环加载次数Ni和压电悬臂梁的电压上升率λi的条件下，可预测压电悬臂梁的剩余寿命。表1是上述三个试验件的预测寿命与实际寿命的比较。结果表明，该模型可以有效预测压电悬臂梁的剩余寿命。

表1 压电悬臂梁的寿命预测结果

3 误差分析

(7)

图10描述了寿命预测误差η与损伤率Di的关系。结果表明，损伤率Di值小于0.4时，最大误差达到62.87%，最小误差值为3.6%；损伤率Di值在0.4～0.8区间时，预测误差小于15%；损伤率Di值在0.8～1.0区间时，预测误差小于5%。因此，该模型虽然可以用来预测压电悬臂梁的剩余寿命，但是由于试验件初始状态不尽相同，当压电悬臂梁的损伤率Di值小于0.4时，预测误差较大。

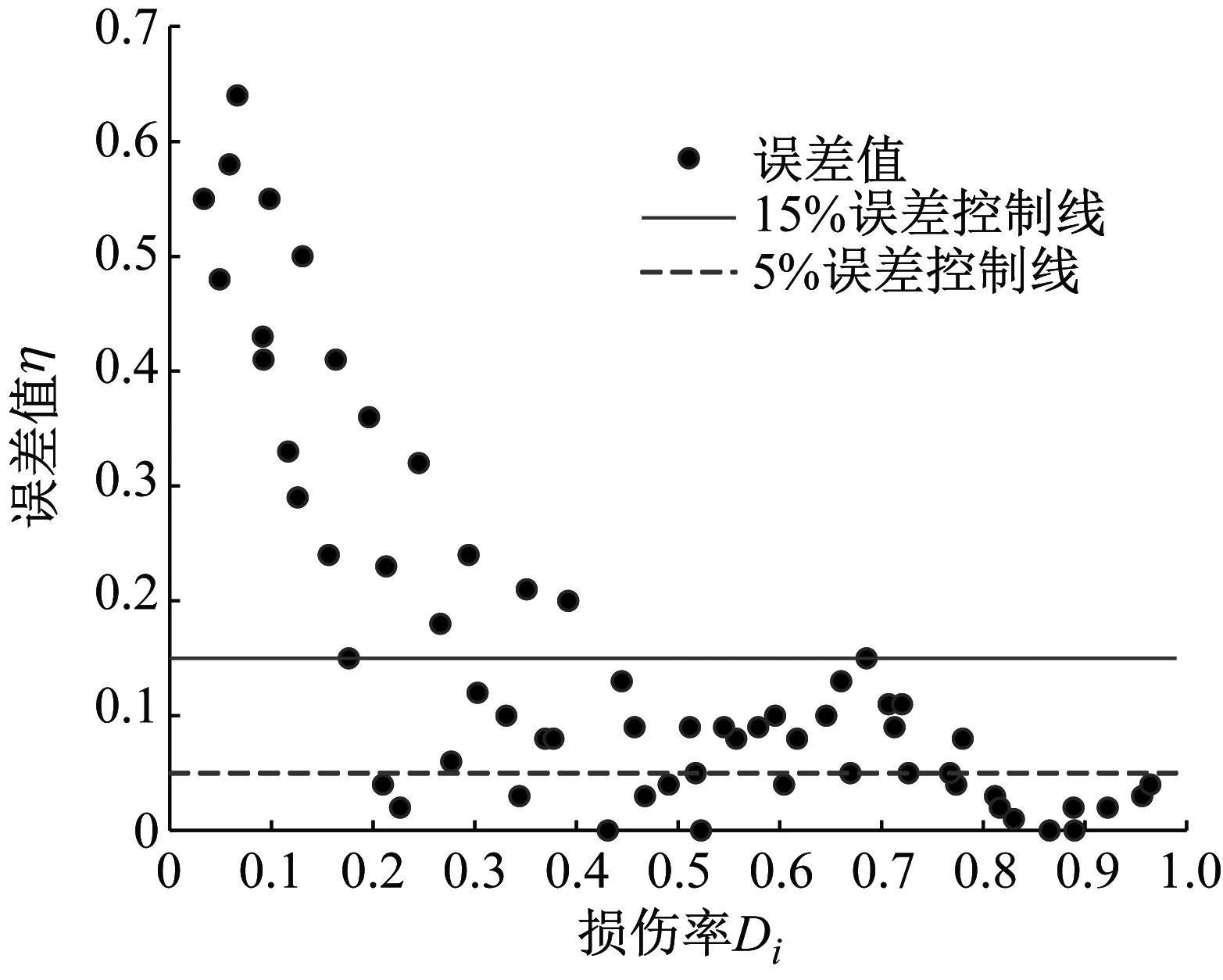
图10 预测结果误差值与损伤率的关系

4 结 论

在测试压电悬臂梁的共振频率、发电电压和循环加载次数的基础上，分析了共振频率、发电电压和循环加载次数之间的关系，结合共振频率下降率与压电悬臂梁振动损伤累积的内在联系，定义了压电悬臂梁的损伤率，建立了损伤率与发电电压上升率的关系模型，提出了基于电压的压电悬臂梁剩余寿命预测模型。主要结论如下：

(1) 共振频带激励下压电悬臂梁的发电电压随循环加载次数的累加而逐渐增大，当压电悬臂梁临近失效时，电压上升率陡然增加。

(2) 压电悬臂梁的共振频率随循环加载次数累加逐渐下降，压电悬臂梁损伤至失效时，共振频率降至初始值的75%。

(3) 已知当前循环加载次数以及电压上升率的条件下，基于电压的压电悬臂梁剩余寿命预测模型可有效地预测压电悬臂梁的剩余寿命。由于试验件初始状态的差异，当损伤率Di值小于0.4时，预测误差较大。