基于BRB的铁路双柱式超高墩连续梁桥横向减震研究

漆启明， 邵长江， 黄 辉， 王应良， 戴晓春， 韦 旺

(1. 西南交通大学 土木工程学院， 成都 610031； 2. 中铁国际集团有限公司， 北京 100039；3. 中铁二院工程集团有限责任公司， 成都 610031)

借鉴民用建筑规范关于建筑高度大于100 m为超高层建筑的相关规定[1]，将100 m以上的桥墩称为超高墩。双柱式超高墩是西部复杂艰险山区铁路桥梁经常采用的下部结构形式，如云桂铁路南盘江特大桥引桥(最高墩102 m)、玉磨铁路元江大桥(最高墩154 m)等。鉴于西部山区强震频发，超高墩桥梁可能面临强震的严峻考验，此类桥梁顺桥向一般可通过阻尼器等手段减震，但横向抗震更多依赖桥墩自身延性，这给桥梁抗震设计带来极大挑战。近年来，不少学者尝试将建筑结构中的屈曲约束支撑(buckling restrained brace, BRB)引入桥梁结构，为双柱式桥墩的横向抗震研究提供了新思路。

Usami等[2-3]早期将BRB用于钢桥，借此提出了保险丝的抗震设计理念。其后，El-Bahey等[4]将保险丝理念引入排架墩桥梁的抗震设计和加固，发现BRB在提升排架横向刚度的同时，其芯材屈服耗能可使墩身保持弹性。谢文等[5]的分析表明BRB可以实现极端地震下双柱式高墩的损伤控制。Wang等[6]通过横向布置BRB对排架墩进行抗震改造，使结构表现出较好的耗能能力，墩底剪力得到重分布，增强了结构的抗震性能。Wei等[7]进行了设置BRB双柱式钢管混凝土排架墩的Pushover分析，发现桥墩的横向位移得到有效控制，但会在一定程度上增加墩底剪力。Bazaez等[8]对一座BRB加固的排架墩模型进行了拟静力试验，发现BRB可有效提升构件延性、控制墩身损伤。李晓莉等[9-10]通过增设BRB来实现排架墩的保险丝设计理念，发现可以有效延缓排架墩的屈服过程。张永亮等[11]揭示了BRB对双柱式中低墩的减震机理，Xiang等[13]研究了近断层地震下BRB加固中低排架墩的有效性，Chen等[14]探讨了近场地震下BRB加固双柱式高墩的减震效果及易损性。由上可知，BRB作为结构优先耗能元件的设计理念是可行的，但研究大多集中于中低双柱式墩和排架墩桥梁的抗震加固，在高墩桥梁中的应用研究还较少，关于双柱式超高墩的BRB研究成果未见报道。

不同于中低墩或一般高墩，超高墩相对较柔、自身质量及地震惯性力较大，高阶振型效应更突出[15]，其对BRB作用机理及减震规律也会有所影响。目前，分析高阶振型影响的方法包括非线性静力法与动力增量法对比[16]、单自由度与多自由度建模单墩的比较[17]、振型分解反应谱原理[18]等，但均难以直接用于超高墩非规则连续梁桥。

鉴于此，以某双柱式铁路超高墩大跨连续钢桁梁桥为例，将屈曲约束支撑作为双肢墩身的减震措施，基于非线性时程分析考察不同BRB参数对应墩身的地震响应规律，研究BRB在超高墩中的作用机理及减震效果，通过变墩高桥梁模型和无支撑墩身桥梁模型的地震响应比较，探讨桥墩高阶振型对BRB墩身地震响应的影响。

1 桥梁实例

某大跨铁路连续钢桁梁桥的立面如图1(a)所示，跨径为(38.6+108+151.5+249+151.5+108+25.6)m，全长832.2 m，采用双线高速铁路标准设计。主梁为变高度钢桁架，中支点桁高36.0 m，等高段16.0 m，按二次抛物线变化。主梁采用盆式球钢支座和黏滞阻尼器，布置如图1(b)所示。T0及T5为拱式桥台，P1～P4为双柱式钢-混组合刚架墩，墩高依次为51.0 m、139.0 m、154.0 m和67.0 m。墩身包括两肢“D”形薄壁空心墩，立柱之间沿竖向每隔15 m设置一道“X”形钢支撑(以下简称“X撑”)，P1～P4所设X撑数量依次为2、8、9、3对，如图1(c)所示。为提升墩身耗能及抗震性能，将原方案中的“X”形钢支撑替换为耗能型BRB，如图1(d)和1(e)所示。

图1 桥梁立面图、支座布置及BRB构造示意图(m)

2 结构建模及地震动输入

采用SAP2000软件建立全桥空间动力计算模型，如图2所示。原方案模型中，钢桁架梁、桥墩、承台及双肢墩柱间的X撑均采用梁单元模拟，正交异性钢桥面则等效为板单元。球形钢支座通过双线性理想弹塑性恢复力模型模拟。利用m法考虑桩土相互作用，等代土弹簧的刚度依据桥梁地勘报告和TB 10093—2017《铁路桥涵地基和基础设计规范》[19]计算，本桥m取为120 000 kN/m4。恒载主要包括结构自重和二期铺装。根据GB 50111—2006(2009)《铁路工程抗震设计规范》[20]，罕遇地震发生几率很小，可不计活载的影响；同时，罕遇地震下钢筋混凝土墩身可采用开裂刚度[21]。阻尼器设计参数为C=3 000 kN/(m/s)0.4，α=0.4，采用Maxwell模型模拟[22]。X撑更换为屈曲约束支撑方案时(见图1(d)、1(e))，BRB设计资料参考上海市建筑产品推荐性应用标准DBJ/CT105—2011《TJ屈曲约束支撑应用技术规程》[23]，通过双线性恢复力模型模拟。

(a)全桥单元划分

桥址场地为II类，特征周期为0.45 s。罕遇地震PGA为0.227g，为研究更高烈度地震下双柱式桥墩的地震响应规律，将PGA进一步提高至0.64g(以下简称“极罕遇地震”)。罕遇地震加速度反应谱(ξ=5%)和加速度时程曲线如图3所示。

(a) 加速度反应谱比较

3 BRB墩身的参数优化

屈曲约束支撑主要包括核心单元、约束套筒和填充材料。在强震下核心构件通过芯材屈服而塑性耗能，外部套筒和填充材料则共同限制芯材屈曲，因此BRB具有基本对称和饱满的滞回曲线。芯材等效截面面积Ae和屈服强度fy是控制其减震效果的关键变量，故将两者作为自变量，以安评地震波(PGA=0.227g、0.640g)为地震动输入，探究BRB参数对桥墩横桥向地震响应的影响规律。X撑方案采用矩形空心钢管截面，面积A为45 900 mm2(外轮廓尺寸为5.0 m×5.8 m)，材质为Q345qD。更改为BRB方案后需进行参数优化，其中，芯材等效截面Ae优化范围取2 000～40 000 mm2，芯材类型包括低屈服点钢BLY160、BLY225和普通低碳钢Q235，计算工况如表1所示。BRB的最大变形统一取支撑长度的1/100(150 mm)。

表1 屈曲约束支撑设计参数

3.1 墩顶位移响应

图4为不同PGA下墩顶横向位移随BRB参数的变化规律，其中，Ae=0表示双肢墩柱间不设支撑，同时给出X撑模型(A=45 900 mm2，与BRB比较时A均取定值)计算结果作为对比。图5是Ae为2 000 mm2、40 000 mm2时P2墩顶和墩底位置BRB的滞回曲线。

(a) PGA=0.227g

从总体趋势来看，罕遇地震下，各墩墩顶位移随等效面积的变化趋势差异较大，但Ae>30 000 mm2时，P1、P2和P3(P4为40 000 mm2)的位移响应与X撑方案接近。这主要是因为BRB增加了桥墩的侧向刚度，当Ae增加到一定程度时，BRB的力-位移曲线近似线性(如图5(c)所示)，在芯材面积接近X撑截面面积(A=45900 mm2)前，增加Ae对墩身整体刚度的提升效果减弱。极罕遇地震下，P1和P3位移响应随Ae增加而减小，P2和P4位移响应则是先减小后增加，表明BRB设计参数存在较优值；Ae较大时的墩顶位移仍小于X撑方案，这源于超烈度地震下BRB滞回曲线变得更饱满，芯材屈服可耗散更多地震能量。

(a) P2墩顶(Ae=2 000 mm2)

对比不同Ae工况可知，罕遇地震下，P1在Ae<30 000 mm2、P4在几乎所有工况的墩顶位移均大于X撑方案，而P2和P3的墩顶位移在大部分Ae工况小于X撑墩身响应。出现上述现象的原因在于：高墩P1(高51 m)和P4(高67 m)在罕遇地震下的横向位移较小，BRB的轴向位移量有限、耗能较少，因此BRB对墩顶位移的改善不如X撑(刚度更大)的效果好；超高墩P2和P3在罕遇地震下的墩顶位移比P1、P4更大，采用合理芯材面积(如15 000 mm2)时的BRB耗能较多，对位移的减震效果优于X撑方案。极罕遇地震下，高墩P1和P4的横向位移相比罕遇地震增加了2倍以上，BRB因轴向变形更大而耗能更多，此时P1和P4的墩顶位移小于X撑方案；类似的，超高墩P2和P3的横向位移也大幅增加，当芯材面积Ae较大时仍有较好的位移减震效果。需强调的是，地震下高墩和超高墩的高阶振型影响不可忽略，其对BRB的减震效果会有一定影响，这一主题将在后文进行探讨。

对比不同芯材工况可知，采用BLY160(fy=160)时的墩顶位移响应相对BLY225、Q235两种芯材更小，这是因为Ae相同时三种芯材的附加刚度Ke相近，但BLY160更容易屈服耗能。罕遇地震下，当Ae增大到一定程度后，三种芯材响应趋于一致，此时BRB轴向刚度较大而地震轴力不大，三种BRB的力-位移曲线均近似直线。极罕遇地震下，BRB的轴力响应剧增，BLY160型BRB的耗能效果最好。

3.2 墩底弯矩响应

图6为不同PGA下墩底(单肢墩柱的墩底空心倒角上缘[24])弯矩随BRB参数的变化规律。

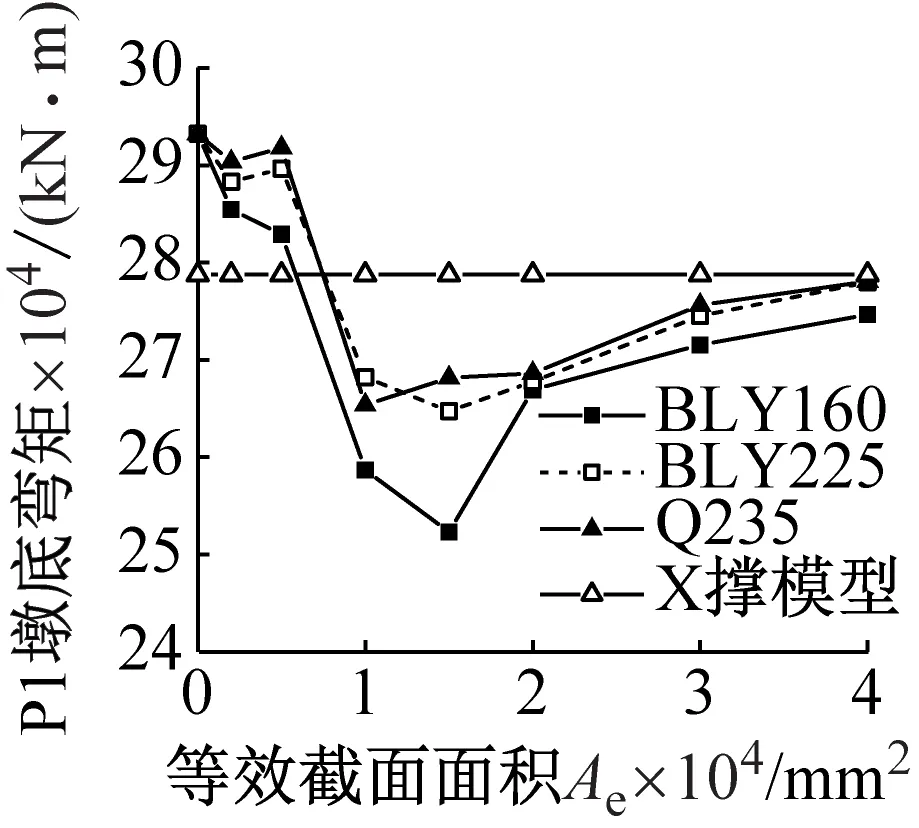
(a) PGA=0.227g

罕遇地震下，P2和P3在Ae>30 000 mm2、P1和P4为Ae=40 000 mm2时的墩底弯矩与X撑方案响应一致。不设横向支撑(Ae=0)时的墩底弯矩比BRB、X撑方案都大，其原因在于双肢墩柱间支撑的存在改变了墩身传力路径，将部分弯矩转化为墩身支点处的剪力，最终成为BRB或X撑的轴力。在Ae到达一定值前(如30 000 mm2)，除P1外的各墩墩底弯矩响应均比X撑方案更大，这主要是因为该范围内BRB较X撑转化的弯矩响应更小且其耗能有限(如图5(a)所示)。对比罕遇地震下Ae为2 000 mm2和40 000 mm2的BRB滞回曲线(如图5所示)发现，尽管前者的BRB滞回更饱满，后者近似直线，但前者的墩底弯矩响应反而更大，其原因是Ae较小时芯材屈服耗能有限，对墩底弯矩改善不如提高支撑刚度的效果明显。在Ae过小或过大时，采用三种芯材BRB的墩底弯矩响应接近，Ae过小时的结果是因为滞回面积较小，芯材屈服耗能对墩身响应影响有限，Ae过大工况是因为罕遇地震下各芯材力-位移曲线趋于线性且刚度接近。

极罕遇地震下，各墩墩底的弯矩变化规律不同于罕遇地震工况。P1地震响应均小于X撑方案，其中BLY160芯材弯矩响应随Ae增加逐渐减小，而BLY225和Q235两者在Ae=20 000 mm2出现最值。P2、P4随BRB参数的变化规律与P1接近，但Ae较小时的墩底弯矩比X撑方案更大，其原因与罕遇地震情况类似。P3的弯矩随芯材等效面积大致呈线性降低。此外，极罕遇地震下，Ae>20 000 mm2时的墩底弯矩仍可得到有效降低，这是因为BRB将墩身部分弯矩转化为支撑杆件的轴力，同时芯材塑性滞回耗能较多。

3.3 墩底剪力响应

图7为不同PGA下墩底剪力随BRB参数的变化曲线。罕遇地震下，随着芯材面积Ae的增大，P1、P2和P4的墩底剪力呈上升趋势，且趋近于X撑方案，这与弯矩响应相比，大致呈现相反趋势，说明了传力路径的改变。究其缘由，Ae增加使得双肢墩柱横向约束不断增强，BRB轴力的水平分量使得桥墩截面的剪力增大，加之罕遇地震下BRB为弹性状态，无塑性耗能削减增加的剪力。

极罕遇地震下，随着BRB芯材屈服耗能，各墩剪力响应均小于X撑方案；P2、P3在Ae>20 000 mm2后的剪力响应变化趋于平缓，而BLY160芯材的剪力响应出现降低。总体而言，墩身采用BRB或X撑后，墩身原来的弯矩部分转变为剪力，一定程度上会增大墩底的剪力响应。因此，在进行此类桥梁抗震设计时应该关注桥墩的抗剪性能，避免空心墩身在强震作用下发生剪切破坏。

(a) PGA=0.227g

3.4 墩底轴力响应

图8为不同BRB参数时墩底最不利轴力的变化曲线，并约定轴力以受拉为正、受压为负。由于轴力变化均与Ae正相关，在此仅给出P1、P2墩的轴力响应。与无支撑方案(Ae=0)相比，在“D”形双肢墩身间设置BRB会使墩底轴力响应发生显著改变。罕遇地震下，随着Ae的增大，墩底轴力呈单调上升趋势，同弯矩和剪力一样也接近X撑方案的结果；P1的墩底轴力随Ae增加由压力变为拉力，P2的轴压力也不断减小，这对抗震是不利的；结合图6(a)和图7(a)发现，罕遇地震下采用X撑方案的P2墩底弯矩相比BRB工况更小，这在一定程度上是以增加P2墩底剪力和不利轴力为代价的。极罕遇地震下，墩底轴力变化趋势与罕遇地震工况类似，但更强地震下屈曲约束支撑芯材屈服，塑性耗能很大程度地改善了墩底的不利轴力；结合图7(b)可知，即使Ae较大时，墩底剪力相比X撑方案也有较好的减震效果。

(a) PGA=0.227g

综上所述，兼顾罕遇地震、极罕遇地震下的耗能，以及构件受力稳定性，BRB芯材取BLY160、Ae取20 000 mm2时，外观尺寸为5.3 m×5.3 m，与X撑截面的外轮廓尺寸接近。此时，各墩顶位移和墩底弯矩的减震效果较好，同时墩底剪力、轴力增幅相对较小。

3.5 BRB减震效果

将Ae取20 000 mm2、芯材取BLY160的BRB方案工况与原X撑方案地震响应比较，进一步探究BRB的减震效果。表2为极罕遇安评地震下墩顶位移和墩底内力的减震率，即(X撑方案地震响应-BRB方案地震响应)/X撑方案地震响应。采用BRB后，墩顶位移均有所减小，P2墩顶减震率高达29.4%(如图9所示)；但同为超高墩的P3位移减震率仅为6.3%，高墩P1和P4的位移减震率也不超过8%。各墩轴力的减震效果非常显著，超高墩P2和P3的轴力减震率更是高达81.9%、104.2%。高墩P1和P4的墩底剪力减震率近30%，超高墩的墩底剪力减震率也超过13%，大大缓解了薄壁空心墩的剪力需求。极罕遇地震下各墩的墩底弯矩减震率较小，超高墩P3更是略微放大了弯矩响应，且与P3的墩顶位移响应规律不再一致，其可能原因是高阶振型的影响，将在3.6节专门探究。

表2 极罕遇地震下桥梁墩顶位移及墩底内力响应的减震率

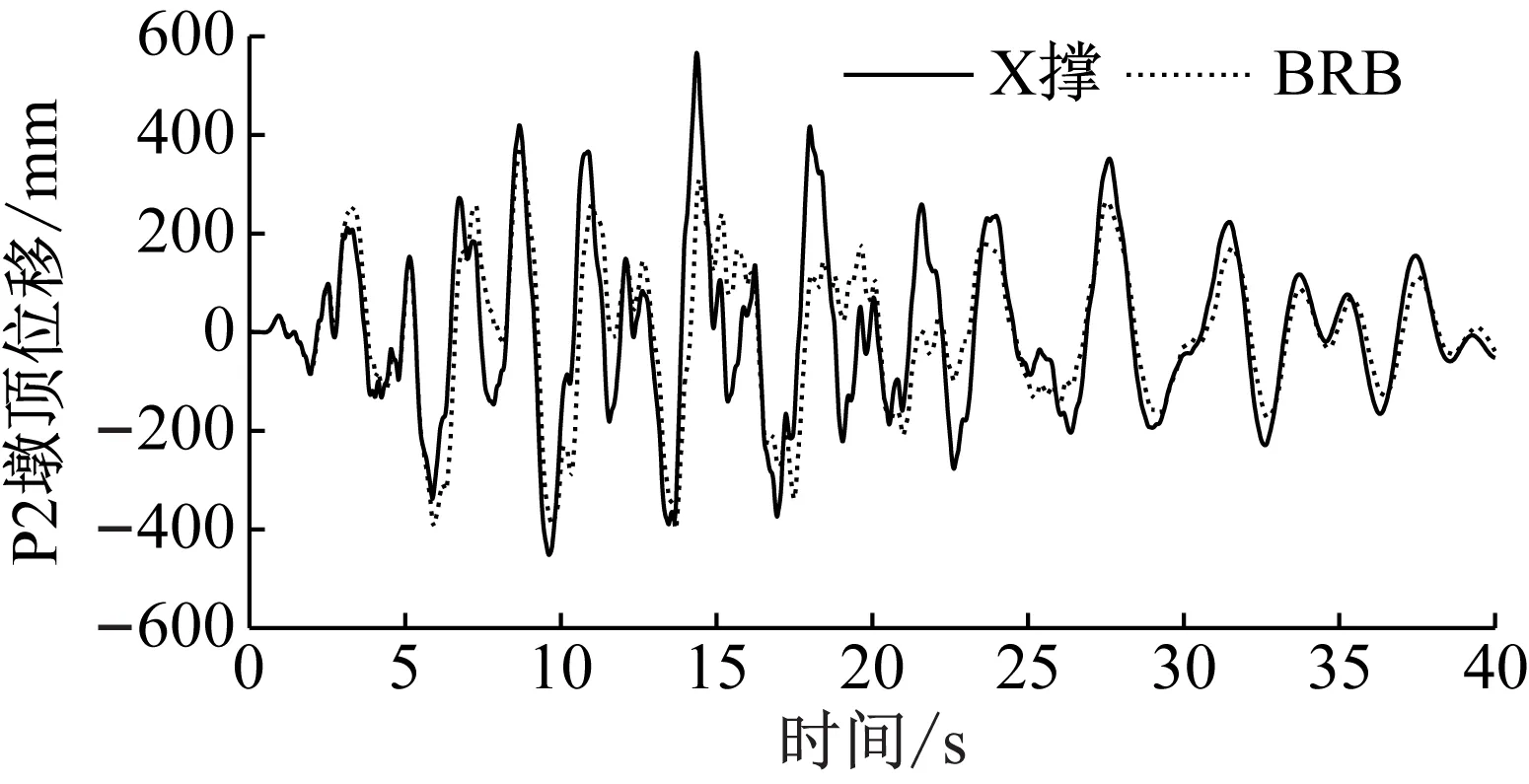
图9 桥墩P2的墩顶位移时程曲线

需指出的是，截面的抗弯能力与所受轴力密切相关。考虑到BRB对轴力的改善，相应的截面抗弯强度也会增强，为此图10给出了超高墩P2、P3墩底截面的PM滞回曲线与截面PM等效屈服包络图。可见，X撑方案P3的墩底弯矩峰值虽更小，但其PM滞回曲线已突破等效屈服包络，构件进入了等效屈服状态；而BRB方案的P3墩底弯矩虽然略大，但仍没有等效屈服，表明BRB可有效改善墩底受弯行为。

图10 桥墩P2、P3的墩底截面PM曲线

4 高阶振型对BRB墩身的影响

对于超高墩，高阶振型对地震响应的影响通常不能忽略，墩顶和墩底的地震响应规律尚不能完全揭示BRB的减震行为。为此，以固定墩P2的8个X撑为基准，超高墩P2和P3逐个减少X撑个数(间距15 m)，且高墩P1和P4依次等比例分别减小5.5 m和7.2 m。以安评地震波、Northridge和Kobe地震波为输入，分别得到各墩高X撑模型(A=45 900 mm2)和BRB模型(Ae=20 000 mm2、芯材为BLY160)的地震响应，结合无支撑模型的计算结果，探明高阶振型的影响。

4.1 墩身振型变化规律

表3以X撑方案为例比较了不同墩高P2、P3的动力特性，分析可知：P2在原墩高减至4个X撑墩高间，中墩P2、P3的一阶横向弯曲振型一致，且伴随主梁一阶正对称侧弯，仅周期、质量参与系数逐渐减小；在P2降低至2个X撑墩高时，P2、P3的一阶侧弯不再同步，分别出现在第四振型和第三振型。桥墩二阶横向弯曲在原墩高时也同步出现(伴随主梁三阶正对称侧弯)，但墩高降低后不再一致，P2依次出现在85、216、307，对应周期从0.761降至0.129；桥墩P3因高度更大，该振型出现序号出现更早且对应周期相比P2稍大。当P2墩高降至79 m时，中墩四阶横向弯曲不再出现，降至49 m时三阶横向弯曲同样不出现，表明高阶振型的影响逐步降低。然而，超高墩在三阶、四阶横向弯曲振型的质量参与系数仍较高，充分说明强震可能会激发超高墩更多的高阶振型。

表3 不同高度中墩P2、P3的典型振型

4.2 墩身位移规律

图11为极罕遇地震下不同高度中墩的墩身位移包络。当不设支撑时，单肢墩柱相对更柔，原墩高P2、P3的墩身位移包络近似二阶弯曲和三阶弯曲振型，而设置BRB和X撑后包络图更接近线性。支撑的存在使得双肢墩柱横向协同受力，减小了单肢墩柱的自由长度，增强了横桥向刚度，由此有效抑制了超高墩的高阶振型。受高阶振型影响，139 m中墩P2在无支撑时的墩顶位移小于X撑方案，但在120 m高度范围内无支撑工况仍大于X撑墩身；BRB附加侧向刚度不如X撑，但因BRB耗能使得原墩高P2的整个墩身位移反而更小；当P2高度降至109 m仍呈现上述规律，但墩高减小为79 m时规律显著变化，无支撑墩身位移最大，BRB次之，X撑最小，其可能原因是该墩高加之空心截面使得铁路桥墩横向刚度大，BRB塑性耗能减小，对位移减震不如X撑附加刚度效果突出。

图11 中墩墩身位移包络随墩高的变化

对于桥墩P3，无支撑墩身位移在各高度均大于设置支撑情况；154 m时的BRB墩身在靠近墩顶的位移小于X撑方案，但124 m时的X撑墩身在靠近墩顶的位移更小；当P3减小至94 m时，X撑墩身位移略小于BRB方案，与对应P2的规律一致。综上可知，随着墩高减小，高阶振型效应逐渐减弱，墩身位移响应受横向支撑的影响更大。

4.3 墩身剪力规律

图12为极罕遇安评地震下不同高度中墩的墩身剪力包络。图13为Northridge和Kobe地震下原中墩在PGA为0.227g、0.38g、0.64g时的墩身剪力包络。

图12 中墩墩身剪力包络随墩高的变化

(a) Northridge地震波

各高度桥墩在靠近墩顶均出现剪力的急剧变大，这是双肢墩柱墩顶的RC横梁所致。受高阶振型影响，墩身剪力包络呈现凹凸交替变化，随着墩高的减小，剪力分布逐渐趋于双折线，而设置支撑后凹凸变化也有所缓解，以上两方面均体现高阶振型效应的削弱。

对于原墩高P2和P3，墩身在中上部的剪力包络图近似垂线，在约1/3墩高范围内不断增加。对于P2，X撑墩身在139 m时的剪力响应最大，应用BRB后剪力响应明显改善；109 m、79 m、49 m墩高时，BRB墩身在下半部分相比X撑方案更有利，墩底减震率分别为21.8%、16.2%、11.6%，而在墩身上半区域则呈相反规律。对于P3，单肢墩柱比P2高15 m，高阶振型更显著，无支撑墩身在154 m时的剪力响应远大于设置支撑结果；此外，124 m、94 m及64 m时设置两类支撑的P3墩身剪力响应规律同对应高度的P2类似。随着PGA的增加，墩身剪力包络图的凹凸交替更加明显，如Kobe地震下无支撑P3墩身出现数个拐点，强震下高阶振型的影响会更显著。

相比无支撑工况，“X”形支撑承受的轴向力会增大节点处的剪力；同时，支撑抑制了高阶振型，可能会一定程度上减小墩身剪力；地震作用下，上述两种效应部分抵消，并共同影响墩身剪力包络图。总体上，原墩高P2设置支撑后的墩身剪力响应更大，而原墩高P3设置支撑后的剪力响应更小。安评波和Kobe波作用下X撑方案在距墩底一定范围的墩身剪力比BRB工况更大，Northridge波的结果差异较小，主要原因在于“X”撑刚度与高阶振型抑制、BRB塑性耗能作用效果的不同步。

4.4 墩身弯矩规律

图14为极罕遇安评地震下不同高度中墩的墩身弯矩包络。图15为Northridge和Kobe地震下原中墩在PGA为0.227g、0.38g、0.64g时的墩身弯矩包络。

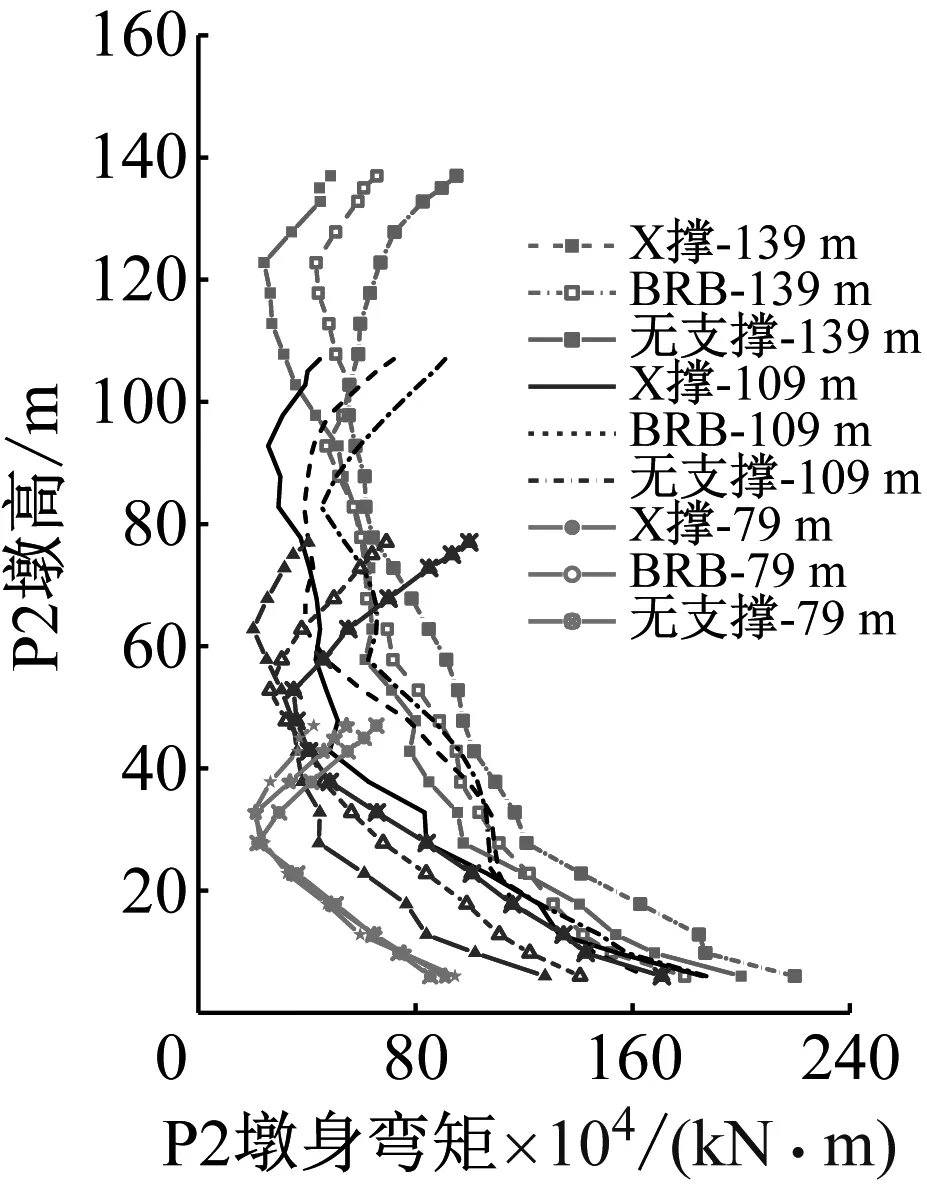
图14 中墩墩身弯矩包络随墩高的变化

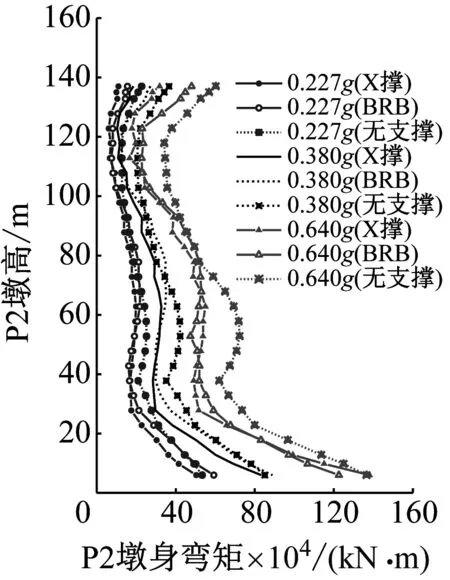
(a)Northridge地震波

同位移、剪力一样，墩身弯矩受高阶振型的影响也非常显著。原墩高P2和P3沿墩身的弯矩包络出现多个拐点，特别是P3在无支撑状态下墩身弯矩包络非常饱满；随着墩高的减小，高阶振型影响减弱，弯矩包络线由凹凸交替逐渐趋于双折线分布。注意到，各墩靠近墩顶的弯矩也较大，究其原因，双柱式桥墩往往有很强的墩顶横梁，单肢墩不再是悬臂构件，靠近横梁处会出现较大弯矩，且随墩高减小而愈加明显。

相比无支撑方案，设置BRB或X撑均可减小墩身弯矩响应：一方面是因为支撑使得单肢墩柱自由长度由全长减小至15 m，有效抑制了高阶振型的影响；另一方面，支撑改变了双肢墩柱的传力路径，使得部分弯矩转化为支撑连接处的剪力和轴力；以上两方面机制对墩身弯矩的正面作用效应具有一致性。然而，也会使节段内墩身在横向地震下承受更大的拉压轴力(见图8)。

相比X撑方案，BRB模型会适当增加墩身的弯矩响应，当减小为一般高墩时，该现象主要集中于双折线包络图的上半段。原墩高P2和P3的墩底弯矩减震效果不佳，如表2中P3墩底的减震率为-3.5%。这是因为BRB提供刚度相比X撑更小，对高阶振型的抑制效果更弱，BRB墩身的高阶振型效应更强烈；此外，BRB在支撑节点处对墩身弯矩的转化较X撑更少；综合以上两方面因素，采用BRB后会适当增大墩身弯矩响应。超高墩墩身中上部的放大效应更是明显，如极罕遇安评地震下(见图14)，P2在42 m高度处的弯矩减震率为-22%，P3在38 m处的减震率高达-39%。然而，BRB可以有效改善墩身的轴力，进而增强截面抗弯能力。图16为上述截面的PM滞回曲线和等效屈服包络。尽管BRB模型的截面弯矩响应幅值较大，其PM滞回曲线却未突破等效屈服包络，墩身整体处于弹性状态；X撑墩身的弯矩值虽较小，但因截面抗弯能力的削弱，已进入等效屈服状态。

图16 中墩P2、P3的关键截面PM曲线

5 结 论

(1) 设置BRB或X撑后可增加墩身侧向刚度，桥墩横向传力路径发生变化，地震作用下原墩身部分弯矩会转化为墩身支点处的剪力和轴力。

(2) BRB选型应兼顾组成构件的稳定性和耗能要求，罕遇地震下BRB通常难以充分发挥耗能功效，位移和内力响应随Ae增加而不断趋于X撑方案。

(3) 极罕遇地震作用下，BRB滞回曲线饱满，塑性耗能可有效减小墩顶位移和墩身不利轴力响应，BLY160低屈服点芯材BRB相对普通X撑更为有利。

(4) BRB模型在极罕遇地震下的弯矩响应相比X撑方案更大，但BRB墩身不利截面的PM滞回曲线并未超过等效屈服包络，墩身整体保持弹性状态。

(5) 受高阶振型影响，BRB墩身中部的剪力、弯矩响应包络凹凸交替变化，随着墩高的减小，影响程度逐渐减小，墩身剪力、弯矩包络近似双折线。

(6) 综合PM能需对比及墩身剪力响应的改善，BRB墩身的减震效果非常显著。因此，后续研究将聚焦X形BRB的具体构造及实施，为今后双柱式超高墩的横向减震设计提供切实可行的手段。