参数异变性对非线性轴向加速梁系统横向振动特性的影响

杨 琼， 褚衍东， 徐 璐， 李险峰

(1. 兰州交通大学 机电工程学院， 兰州 730070； 2. 兰州交通大学 数理学院， 兰州 730070；3. 兰州交通大学 甘肃省轨道交通装备系统动力学与可靠性重点实验室， 兰州 730070)

随着现代科学技术的发展，梁结构在工程科学领域的应用越来越广泛，如锯、磁带、机械臂、飞机机翼等都涉及梁结构的运动。但梁结构轴向运动的横向振动会导致机械设备效率降低，折损机械设备的使用寿命。因此，在实际应用中对轴向运动梁稳定性的研究就变得越来越重要。Wickert[1]利用一维梁理论建立了一类非线性轴向运动梁的力学模型。丁虎等[2]借助微分求积方法，在数值上研究了不同边界条件下轴向运动黏弹性梁的横向受迫振动及稳态响应问题。Chen 等[3]借助 Timoshenko 理论的多尺度方法研究了轴向加速黏弹性梁在参数共振作用下的动态稳定性问题。丁虎等[4]借助近似解析摄动法研究了非线性轴向运动黏弹性 Rayleigh 梁的横向非线性参数振动问题。Özhan[5]研究了外激励对轴向加速梁系统非线性振动特性的影响。Bagdatli等[6]研究了非理想支撑条件下轴向运动梁的线性振动问题。 Ding 等[7]提出了新的垂直弹性支撑边界，定义了垂直弹簧支撑黏弹性梁的传递率，开启了弹性结构隔振研究的开端。Wang 等[8]研究了垂直悬臂结构的内部共振问题。为了更加清楚地研究系统的运动机理,许多学者将混沌和分岔理论广泛应用到轴向运动梁模型的研究中。Ravindra等[9]研究了超临界状态下轴向加速梁的混沌和 pitchfork 分岔现象。Pellicano等[10]分析了次临界速度和超临界速度范围内受质量轴向传输简单支撑梁的动力学行为。Yang等[11]研究了具有几何非线性轴向加速黏弹性梁的分岔和混沌问题。Ding等[12]借助数值仿真手段研究了轴向平均速度和速度扰动幅度对轴向加速黏弹性梁横向运动中非线性动力学行为的影响。Ding 等[13]采用高阶伽辽金截断法和微分-积分法研究了轴向加速黏弹性梁在超临界状态下的分岔和混沌问题。Yan 等[14]研究了轴向加速黏弹性 Timoshenko 梁的稳态周期响应和混沌分岔问题。Sahao等[15]研究了非线性组合参数激励下横向移动弹性梁的稳定性和各种分岔现象。

上述文献仅研究了单参数变化对轴向加速梁系统动力学特性的影响。双参数耦合条件下，非线性系统更加丰富的动力学现象[16-20]已被大量学者所研究，但对轴向加速梁系统在双参平面内分岔特性的研究还鲜有报道。本文以一阶 Galerkin 截断法[21]离散的轴向加速度梁为研究对象，分析了轴向平均速度、速度扰动幅值、黏滞阻尼、速度扰动频率变化时，系统的稳定性和分岔现象。借助计算机仿真方法，研究了速度扰动幅值和速度扰动频率同时变化对系统振动特性的影响。

1 轴向运动梁模型

轴向运动梁模型如图1 所示，其中挠曲刚度为EI，轴向刚度为EA,在两个距离为L的简单支撑之间以速度v运动,P为施加的张力，ρ为梁的密度，v为轴向移动速度，u(x,t)和(x,t)分别表示梁中点的轴向位移和横向位移。忽略梁在平面以外的运动及剪切形变。

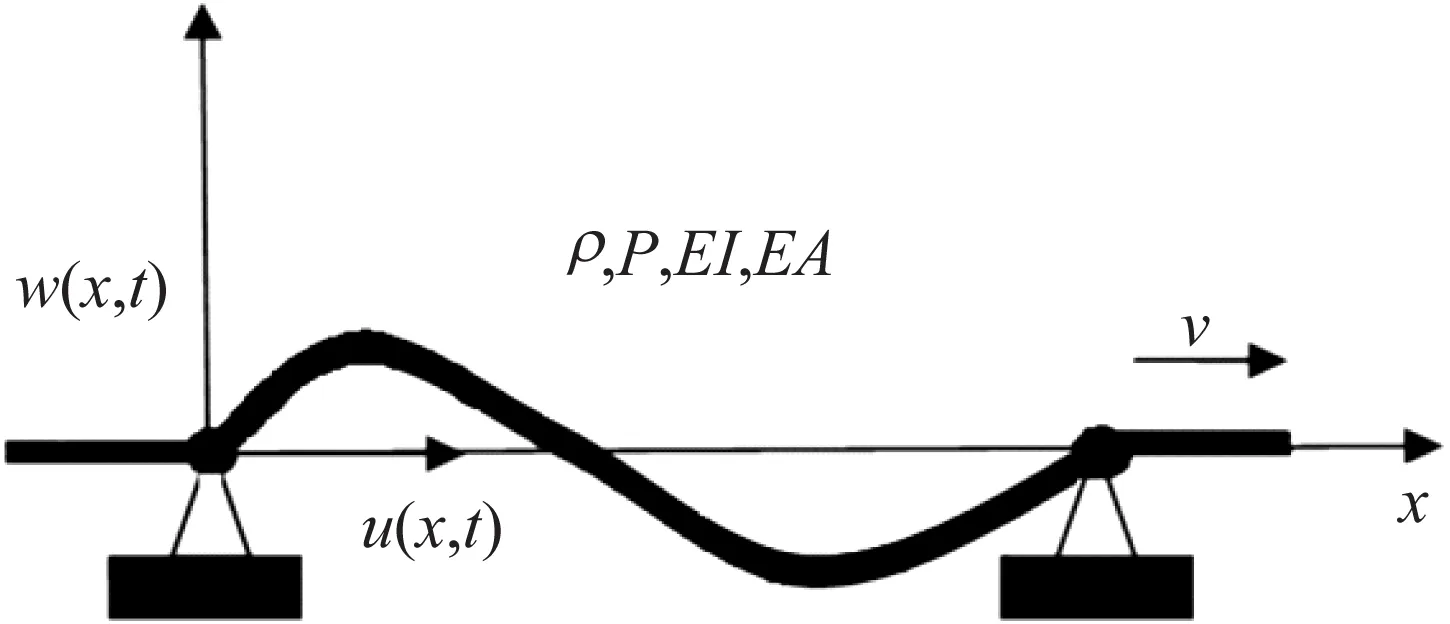
图1 非线性轴向运动梁的模型图

基于有限变形原理，非线性轴向应变的 Lagrangian 函数为

(1)

由 Hamilton 原理可得

(2)

其中动能

(3)

势能

(4)

下标“，”表示对其后面的变量求偏微分，下面引入无量纲变量及参数如下

(5)

(6)

式中：E为杨氏模量；A为截面面积；I为惯性矩；v*为轴向移动速度；v1为纵向刚度；vf为抗弯刚度参数，相关材料参数详见文献[22]。

为便于计算，下面省略变量上的星号。利用 Hamilton 原理及准静态近似，引入黏滞阻尼系数ζ，可得无量纲化轴向加速梁横向振动的控制方程

tt+2ζwt+2vwxt+v2xx+vtx-xx+

(7)

假设轴向运动梁的边界条件为

(0,t)=(1,t)=0,，xx(0,t)=，xx(1,t)=0

(8)

令

(x,t)=h1(t)sin πx

(9)

其中sin πx是第一个特征函数，h1(t)是广义位移。 利用 Galerkin 截断法，得到一阶模态微分方程如下

(10)

当轴向移动速度存在小谐波振荡时

v=v0+εsinΩt，ε<<1

(11)

式中，v0、ε、Ω分别表示轴向平均速度、轴向速度扰动幅值以及轴向速度扰动频率。对式(11) 作如下近似变换

(12)

则式 (10) 可写为

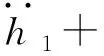
(13)

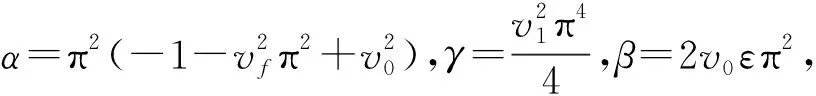
(14)

通过坐标变换

(15)

式 (14) 可写为

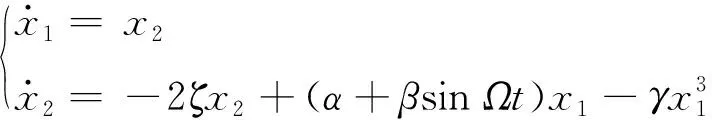
(16)

式中：α表示平均速度参数；ζ表示黏滞阻尼；β表示速度扰动幅值参数；Ω表示速度扰动频率；γ表示非线性刚度参数。

2 单参数变化对轴向加速梁横向振动的影响

2.1 平均速度参数α对轴向加速梁振动的影响

当速度扰动幅值参数β=0时，式(16) 稳态解的方程如下

(17)

命题1非线性系统 (16)的稳态响应与平均速度参数α有如下关系

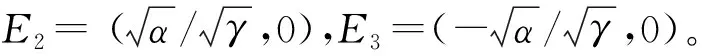
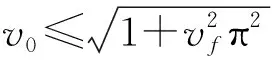
(18)

式 (16) 可写为

(19)

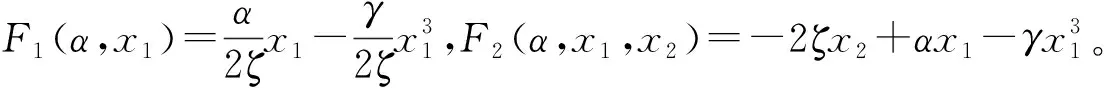
(1)F1(α,x1,x2)和F2(α,x1,x2)为关于(x1,x2)的奇函数；

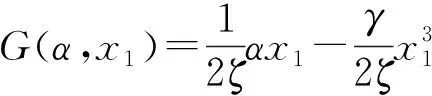
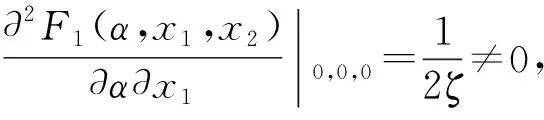
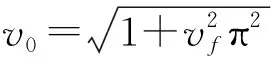
下面讨论式(16) 平凡平衡点E1=(0,0)的稳定性。式(16)在平凡平衡点处对应的 Jacobi 矩阵为

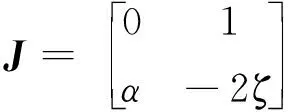
(20)

其特征方程为

λ2+2ζλ-α=0

(21)

于是，有以下结论成立

(1) 当α>0，ζ≠0，平凡平衡点E1=(0,0)为鞍点，即，当轴向平均速度v0满足

时，平衡点处存在稳定流形和不稳定流形，则横向振动始终存在，轴向加速梁系统不会平稳运行。

(2) 当-ζ2<α<0，ζ≠0时，平凡平衡点E1=(0,0)为稳定结点。即，当轴向平均速度v0满足

时，轴向加速梁的横向振动会逐渐减弱，最终在初始位置处横向运动消失，轴向加速梁系统进入稳态响应阶段。

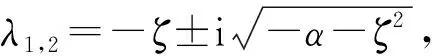
时，轴向加速梁的横向振动周期性的减弱，最终在初始位置处横向振动消失。

2.2 速度扰动幅值参数β对轴向加速梁振动的影响

当β≠0时,式(16)的Poincaré映射会出现 Smale 马蹄型混沌集[25-26]。下面的命题给出了当平均速度参数α=1.0>0时，轴向加速梁系统(16)出现完全失稳屈曲的速度扰动幅值范围。

证明当α=1.0>0时，将式(16)重写为如下形式

(22)

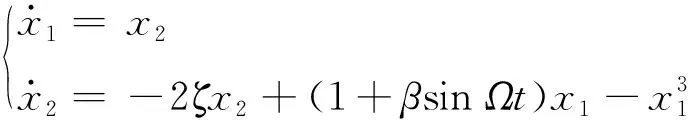
(23)

则对应未扰无黏滞阻尼 (ζ=0,β=0) 系统的哈密顿函数为

(24)

且平凡平衡点(0,0)是鞍点，则存在一个由稳定和不稳定流形形成的同宿轨道。由式(24)可解出

(25)

对式(25)进行积分，可以得到

(26)

从而，同宿轨道的参数化方程为

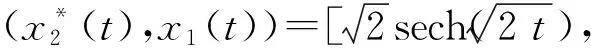
(27)

由 Melnikov 积分可知

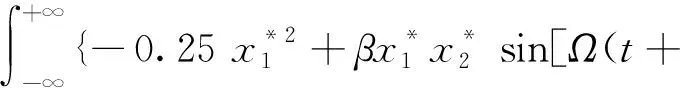
t0)]}dt

(28)

将式(27)代入式(28)可得

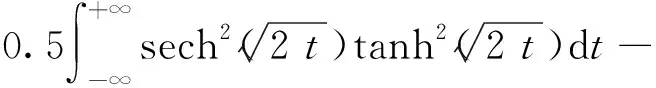
(29)

利用文献[23]中的引理 16.1.2，计算得

(30)

M(t0)有简单零点的条件为

(31)

由文献[23]中的 Smale-Birkhoff 定理可知，当式(24) 成立时，稳定流形和不稳定流形横截相交，式(16)出现 Smale 马蹄型混沌振荡，参见图10(f)。

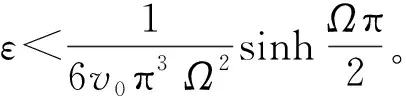
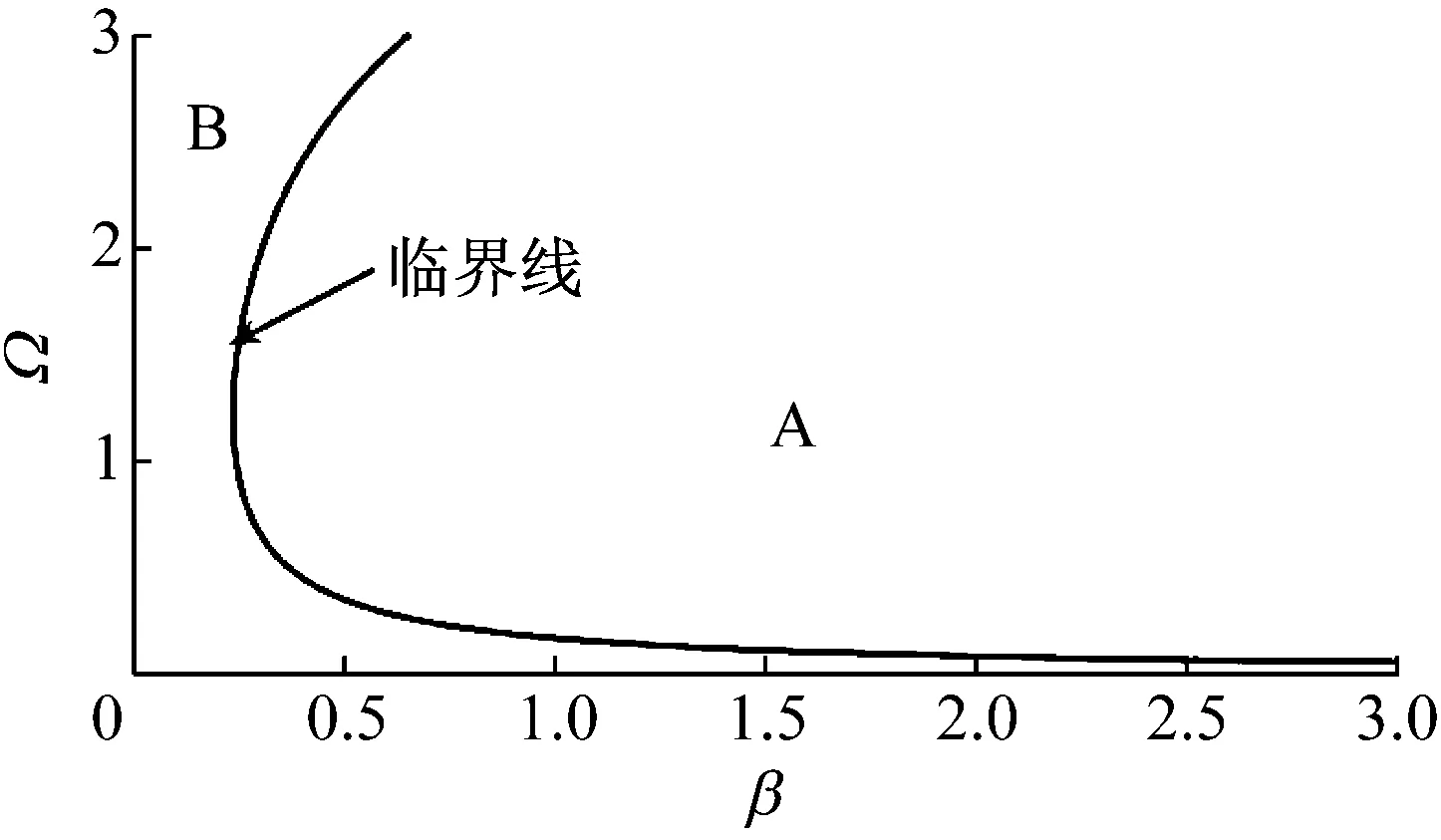
图2 Smale 马蹄型混沌振荡的临界域

2.3 黏滞阻尼ζ对轴向加速梁振动的影响

下面从数值的角度研究了黏滞阻尼ζ对轴向加速梁系统横向振动特性的影响。固定参数α=1.0，β=2.5，γ=1.0，Ω=2.5，初值为(x1,x2)=(0.1,0.1)，其中ζ为分岔参数。

观察图3(a) 可知，当黏滞阻尼ζ在[0.1,1.5]范围内变化时，会出现自相似的分岔结构A1和A2。下面仅以图的一支分岔结构A1为研究对象，即图3(b)。通过观察可知，参数ζ在0.919～0.915的范围内减小时，系统会出现倍周期分岔 (PD 分岔) 现象，当参数ζ减小为ζ≈0.918时，系统出现第一次倍周期分岔，继续减小参数ζ,系统的周期振荡与混沌振荡会间隔出现, 最终当黏滞阻尼减小到ζ=0.1时，系统进入混沌振荡状态。这就说明黏滞阻尼ζ越小轴向加速梁振荡越剧烈。因此，为了尽可能地保证轴向加速梁的稳定运行，我们可以适当的增大黏滞阻尼，例如可以取ζ=1.2。

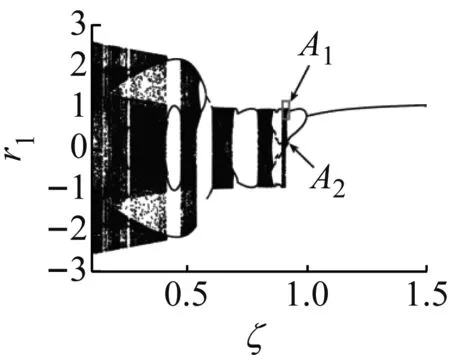
(a)

3 双参数影响下系统的动态演化过程

在本章，我们借助仿真手段同时调谐速度扰动频率Ω和速度扰动幅值参数β，研究轴向加速梁系统 (16)复杂的运动状态。固定部分参数ζ=0.125，α=1.0，γ=1.0，及初始条件(x1,x2)=(0.1,0.1)。借助文献[17]中的方法生成双参数分岔图，通过记录参数平面内不同周期振荡的数目来描述系统更复杂的运动状态[27-28]。当参数β×Ω∈[0,3.0]×[0,3.0]时，式(16)的全局视图如图4 所示，右边的颜色条是一个包含 20 种颜色的调色板，每个小于20 的整数对应的颜色代表各自周期峰值的数目，由于高周期分岔在有限的参数平面内具有密集性，仅靠数值方法很难确定和区分高周期的分岔点。因此我们仅考虑低周期运动特性，将周期数大于等于 20 的周期运动笼统的归类为混沌振荡运动，并用黑色表示。

图4 参数 (β×Ω) 平面中的全局分岔图

为了详细地观察系统的振荡特性，借助逐级放大参数平面区域的方法，可以更加细致的研究高周期分岔在参数平面上的动力学分布。将周期划分变为 50 种，每个小于 50的整数对应的颜色表示周期振荡的数目,黑色表示周期数大于等于 50 的混沌振荡。图5 是图4 中 a 框的放大图，其中参数β×Ω∈[1.976,2.400 2]×[2.743,2.785 03]。通过观察发现，在右上角，周期 2 轨道消失，出现混沌吸引子，这是非线性动力系统出现鞍结分岔 (SN 分岔) 的重要特征，也是连续系统从周期振荡进入混沌振荡的一种方式，即 SN 分岔。沿着图5 中的白线，也可以观察到嵌入在黑色区域的周期振荡现象，这些周期岛类似于圆映射中的 Arnold tongues[29-30]，但它只是嵌入在混沌振荡区域的虾形周期振荡。这些周期的虾形级联具有与 Arnold tongues 相似的性质，即随着参数β的增大，虾形岛形成的周期数集合依次为：周期 4 →周期 10 →周期 6 →周期 14 →周期 8 →周期 18 →周期 10 →周期 22 →周期 12 →周期 26 →周期 14 →…。这里还出现了一个有趣的现象：周期 10 的虾形结构出现在周期 4 虾形结构和周期 6 虾形结构之间，即奇异周期结构的周期数等于两个相邻相似结构周期数之和，在周期 14、周期 18、周期 22、周期 26 上也存在类似的规律。这种规律在 Arnold tongues 中是普遍存在的，但是在虾形结构中这种规律却出现的很少。我们还发现随着虾形结构周期数的增大，虾形结构的宽度是逐渐减小的，并且在周期虾形结构的内部还出现了一些黑色的区域。这个现象还可以通过沿着直线Ω=0.052 8β+2.655 7，β∈[2.0,2.35]的单参数分岔图6 及放大图7(a)、(b)观察到，其中参数β的范围分别为β∈[2.057,2.063]、β∈[2.164,2.172]。也就是说，当参数β在[2.0,2.35]内逐渐增大时，轴向加速梁系统的横向出现周期振荡与混沌振荡间隔出现的现象且周期振荡越来越强，最终导致轴向失稳，但当2.34≤β≤2.35时，轴向加速梁的横向运动进入周期 2 振荡，系统处在比较稳定的运动状态。

图5 图4中 a 框的放大图

图6 沿着图5中白线的分岔图

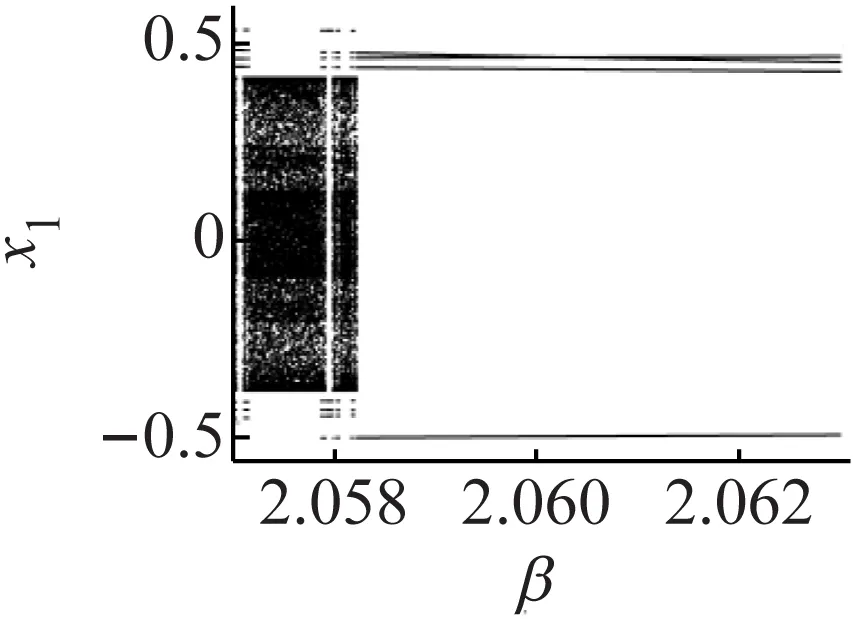
(a

图8(a) 的参数范围为β×Ω∈[1.8,2.2]×[1.02, 1.12]，是图4 中 b 框的放大。也出现了类似的虾形结构，即周期 3 →周期 8 →周期 5 →周期 12 →周期 7 →周期 16 →周期 9 →周期 20 →周期 11 →…。图8(b) 的参数范围为β×Ω∈[1.94,2.06]×[1.065,1.085]，是图8(a) 中白框的放大，它描述了不同类型的奇异周期振荡结构，这些奇异结构是由周期5 振荡的中心体产生的，看起来像是一个尖头虾形结构[31]，这些结构可以用三次多项式的两个标准形式来描述[32]。在这个分裂的虾形结构上，出现了倍周期分岔线，即随着速度扰动频率Ω的减小，系统的运动状态由周期 10 振荡进入到周期 5 振荡，也就是在箭头所指分界线上的各点均会产生 PD 分岔。

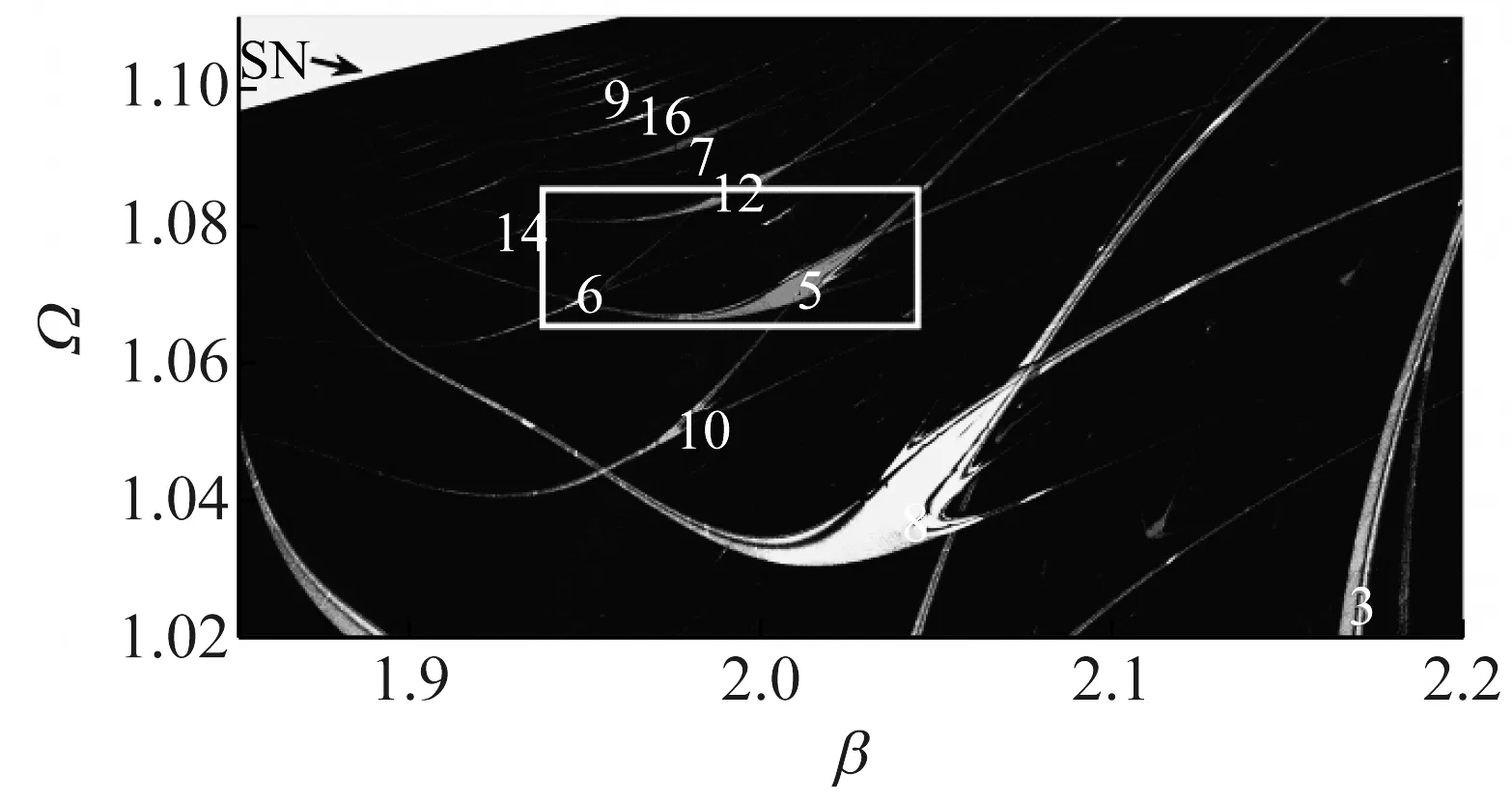
(a)

此外，式(16)还出现了其他进入失稳状态的方式，如图9 (图4 中 c 框的放大图) 中一个依托1×2n周期加倍分岔级联进入混沌振荡的方式，即倍周期分岔 (PD 分岔)。这里的参数范围为β×Ω∈[0.4,0.75]×[2.05,2.45]。通过观察发现嵌入在混沌振荡区域的虾形级联集合，即周期 6 →周期 8 →周期 10 →周期 12 →周期 14 →周期 16 →…，这些周期数序列总是以方差为 2 的等差数列方式递增排列。由于所有的周期吸引子都是以同一种方式进化，在很大的混沌振荡范围内，总会出现沿着一个固定的方向逐渐积累的自相似小虾形周期级联。

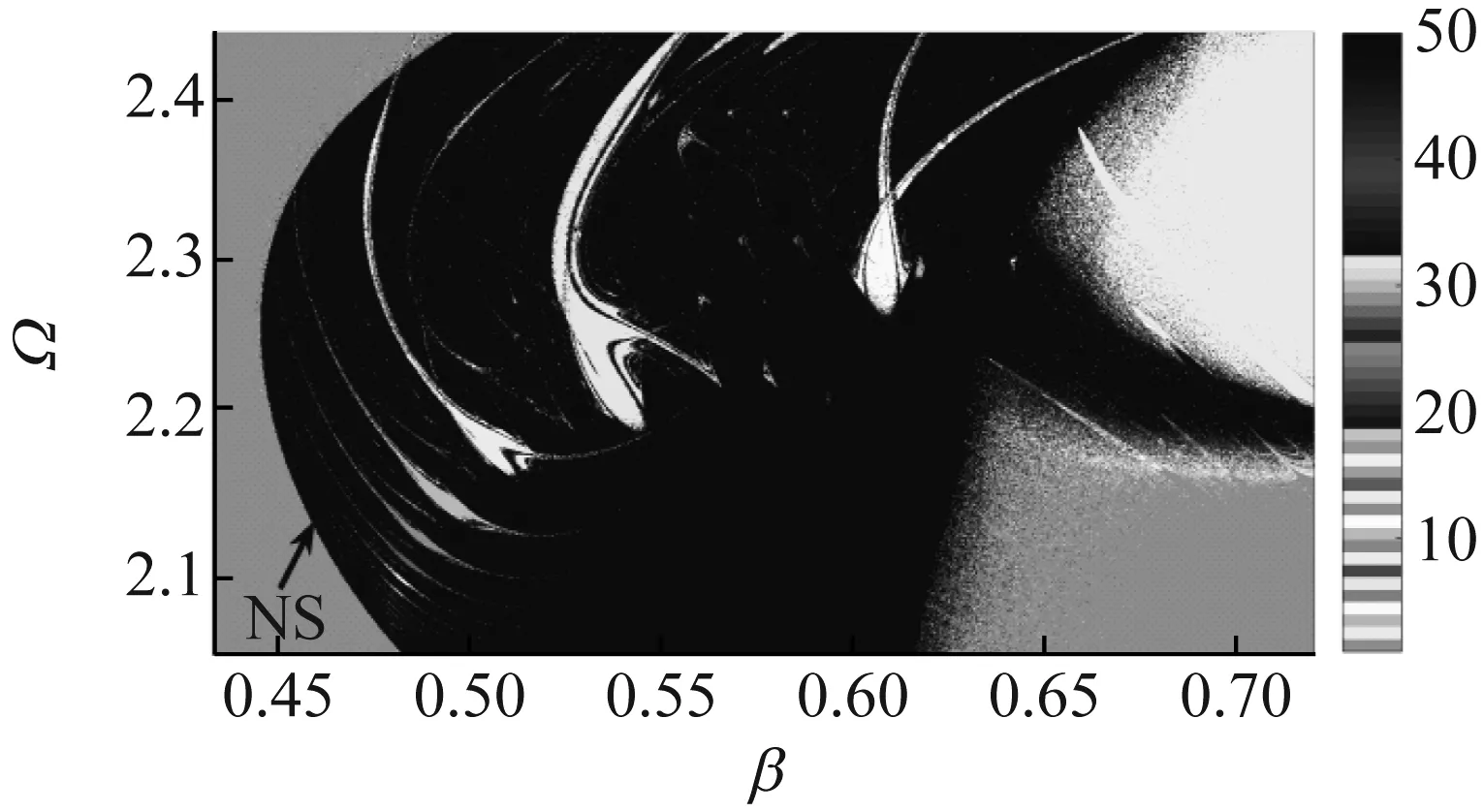
图9 图4中方框c的放大图

图10是图5 中 A、B、C、D、E、F六个可以描述系统周期振荡和混沌振荡状态的 Poincaré 映射图，其中点的个数表示周期振荡数目。这些点的排列顺序与图5 中类 Arnold tongues 性质虾形结构的排列顺序相同，即周期 10 虾形岛出现在周期 4 虾形岛和周期 6 虾形岛之间，周期 14、周期 18、周期 22也满足这种特性。图10(e) 出现了周期振荡吸引子与混沌振荡吸引子的共存现象，其中方框代表周期 4振荡吸引子。图10(f) 是混沌振荡吸引子[33]，此时，β=2.153>0.5299，这与前面第 2 部分的理论结果保持一致。

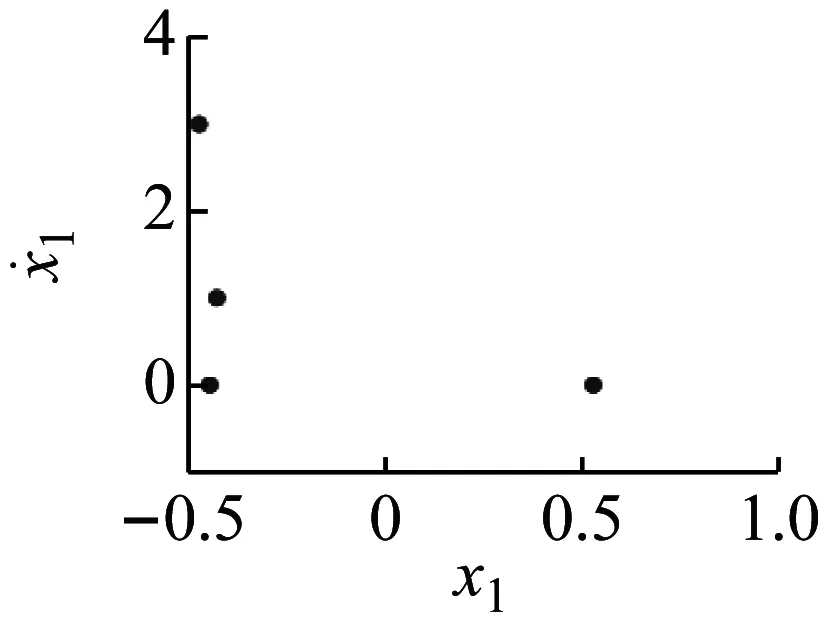
(a) β=2.037,Ω=2.766

4 结 论

本文研究了轴向平均速度、速度扰动幅值、黏滞阻尼、速度扰动频率对一阶 Galerkin 截断后的轴向加速梁系统横向振动特性的影响。主要结果如下：

(1) 当平均速度参数α变化时，轴向加速梁系统会出现 pitchfork 分岔，这说明轴向平均速度v0对轴向加速梁系统横向振动特性有很大的影响。

(2) 随着黏滞阻尼ζ的增大，轴向加速梁系统的运动状态会由原来的混沌振荡状态变成周期振荡状态，最终趋于单周期稳定运动状态。在实际应用中，适当的增大黏滞阻尼，能够尽可能保证轴线加速梁的稳定运行，例如取ζ=1.2。

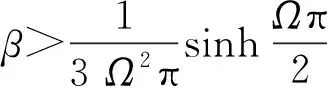
(4) 当速度扰动幅值参数β与速度扰动频率Ω同时变化，轴向加速梁系统出现了丰富的动态演化规律及奇异结构[34](见附录A)。这些结构的周期振荡数目有规律的增加，并且嵌入混沌振荡区域的宽度越来越窄。这意味着在失稳屈曲状态的参数区域中还存在着小范围的周期振荡，而这些嵌入在混沌振荡区域中的小块周期振荡区域，是经常会被设计者忽略的参数区域。因此，为了防止系统出现失稳屈曲现象，在参数选择中应尽量远离共振频率，寻找周期数相对较低区域的参数，尽可能保证系统的平稳运行。

(5) 借助一阶 Galerkin 截断方法，将轴向加速梁系统简化为含参数激励的 Duffing 型振子，可以初步得到系统的定性性质 (分岔类型及混沌的转迁规律)。然而，由于截断阶数较低，使得截断后的系统对原系统的近似效果不够好。因此，在后续研究中，我们将考虑参数异变性对高阶 Galerkin 截断所得系统振动特性的影响。

附录A

奇异结构

图A.1 虾形三角形

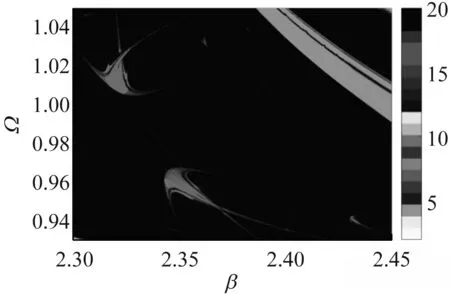
图A.2 对称虾形

图A.3 类混沌之眼

图A.4 虾形的积累