例析等积法的解题技巧

朱红艳

摘要：初中数学中的等积法是一种十分重要的解题思路与方法，其实质是一种转换思想，例如运用“两个三角形等底等高则面积相等”的性质，把一些较复杂的难以直接解决的问题，转化为较简单的能够间接解决的问题，从而使问题得到简捷的解答.本文中结合四类典型实例，探讨和总结了运用等积法解题的方法与技巧.

关键词：等积关系；等积变形；等积互换；等积代换

等积法是等面积法的简称，等积法在初中平面几何类解题中应用十分广泛，例如著名的勾股定理的推导与证明，就是以面积公式及由面积公式推得的相关性质为基础的.运用等积法解题的关键是，对同一几何图形的面积采用不同的分解、计算方法，通过转换与推导得出面积关系式或者线段与角之间的关系式.下面通过典型例题来探讨并总结运用等积法解决相关问题的方法与技巧.

1 运用等积关系求面积

对于不能直接用公式计算的多边形面积类问题，通常是在准确理解题意的基础上，先画出示意图，然后根据多边形的性质与特点，通过添加辅助线，将多边形巧妙地分解为若干个三角形，再求出三角形的面积，最后把若干个三角形相加.解题的关键是充分利用由面积公式推导出的相关性质，寻找图形内或图形之间的关系[1].

例1已知∠ACB=90°，Rt△ABC的三边AC，BC，AB的长分别为三个连续的整数，以AC为直径作圆，交AB于点D，过点D作圆的切线交BC于点E，求四边形ADEC的面积.

解：依题意设AC=x－1，BC=x，AB=x+1.

因为 ∠ACB=90°，所以 AC2+BC2=AB2.

即（x－1）2+x2=（x+1）2.

解得x1=0（舍），x2=4，即x=4.

所以 AC=3，BC=4，AB=5.

如图1，连结CD，因为AC为⊙O的直径，所以 ∠ADC=90°.所以∠ACB=∠ADC=90°.

又因为∠A=∠A，所以△ACD∽△ABC，从而可得ADAC=ACAB.

所以由AD·AB=AC2，可得AD=325=95，于是BD=AB－AD=5－95=165.

因为 12AB·CD=12AC·BC，所以

CD=AC·BCAB=3×45=125.

因为S△ADC=12AD·CD=12×95×125=5425.

因为AC为直径，∠ACB=90°，所以BC切⊙O于点C.

又因为DE切⊙O于点D，所以DE=EC，∠CDE=∠ECD.又结合∠CDE+∠EDB=90°，并且∠ECD+∠B=90°，可得∠EDB=∠B，从而BE=DE.因此EC=12BC.

所以S△DEC=12S△BDC=12×12×165×125=4825.

故S四边形ADEC=S△ADC+S△DEC=5425+4825=10225.

例2如图2，已知△BOF，△BOD，△AOF，△COE面积分别为30，35，40，84，求△ABC的面积.

解：设S△AOE=y，S△COD=x.由面积比关系，列方程组，得

x+35y+84=3040=34，

x35=y+8470.

解之得x=70，y=56.

所以S△ABC=30+40+35+70+84+56=315.

运用技巧：例1首先利用勾股定理及已知条件“三边长分别为三个连续整数”求得三边长，然后通过添加辅助线CD，把四边形ADEC分解为两个三角形，只要求出两个三角形的面积即可得到四边形的面积；例2是运用“数形结合”思想，把几何问题转化为代数问题，根据三角形的面积比列出方程组求解，显得更加简捷.

2 运用等积变形证面积

在一些平面几何证明题中，有时需要证明两个不同图形的面积相等，这时只需要对待证的图形进行简单的分割，利用图形等面积变形或转换的处理，即可使问题得证.

例3如果延长四边形ABCD的各边，使A，B，C，D分别成为DE，AF，BG，CH的中点，那么四边形EFGH的面积是四边形ABCD面积的几倍？

解：如图3，连接AC，BD，BE.因为BA，EB分别是△EBD与△AEF的中线，所以S△BAE=S△BAD，S△EFB=S△BAE.

所以S△AEF=2S△BAD.

同理可得

S△BFG=2S△ABC，S△CGH=2S△BCD，S△DHE=2S△CDA.

所以S△AEF+S△BFG+S△CGH+S△DHE+S四边形ABCD

=2（S△ABD+S△ABC+S△BCD+S△CDA）+S四边形ABCD

=2×2S四边形ABCD+S四边形ABCD.

即S四边形EFGH=5S四边形ABCD.

答：四边形EFGH的面积是四边形ABCD面积的5倍.

例4如图4，已知在四边形ABCD中，AC，BD交于点E，延长DB到点G，使BG=DE，延长CA到点F，使AF=CE，连接FG.

求证：S△EFG=S四边形ABCD.

证明：连接AG，CG.

因为BG=DE，又△ABG与△ADE有共同顶点A，所以S△ABG=S△ADE.

同理，S△AFG=S△CGE，S△CBG=S△CDE.

所以S△CDE+S△CEB=S△CBG+S△CEB.

即S△CDB=S△CEG.

所以S△EFG=S△ABG+S△AFG+S△ABE=S△ADE+S△CEG+S△ABE=S△ADE+S△CDB+S△ABE=S四边形ABCD.

运用技巧：例3和例4都是证明三角形与四边形的面积之间存在某种关系，都运用了等积变形的方法.先将四边形分割成若干个小三角形，而这些小三角形面积又成对相等；最后采用等积代换与组合的方法，证明了三角形与四边形之间的面积关系.

3 运用等积互换证线段

对于有些难以直接证明的两条（或几条）线段相等的问题，可以采用间接证明的方法，先证明两个图形的面积相等，再由这两个图形的相关线段相等，推证出待证的两条线段也相等.

例5如图5，已知D是△ABC内∠BAC平分线上的一点；CE∥DB，交AB的延长线于点E；BF∥DC，交AC的延长线于点F.求证BE=CF.

证明：如图6，设CE与BF的交点为G.连接DG，DE，DF.

因为D是∠BAC平分线上的点，所以∠BAD=∠DAC.过D分别作DM⊥AB，DN⊥AC，M，N为垂足，则DM=DN.

因为CE∥DB，BF∥DC，所以四边形CDBG为平行四边形，于是S△BDG=S△CGD.

又因为BD∥CE，所以S△BDE=S△BDG.

同理，可证S△DCF=S△DCG.

因此S△BDE=S△DCF，即

12BE·DM=12CF·DN.

所以BE=CF.

例6如图7，在△ABC中，点A′，B′，C′分别在边BC，CA，AB上，AA′，BB′，CC′交于点O，且AOOA′+BOOB′+COOC′=92.

求AOOA′·BOOB′·COOC′的值.

解：令x=S△BOC，y=S△COA，z=S△AOB，则

AOOA′=z+yx，BOOB′=x+zy，COOC′=y+xz.

所以

AOOA′·BOOB′·COOC′

=（z+y）（x+z）（y+x）xyz

=z+yx+x+zy+y+zz+2

=AOOA′+BOOB′+COOC′+2.

=92+2=94.

运用技巧：例5、例6运用了等积变换法.例5首先证明了两个三角形面积相等，而这两个三角形的高又是已知且相等的，然后推证出它们的底相等，最后推证出两条线段相等；例6利用了“等底”或“等高”的三角形的面积比，将线段比转化为面积比，最后又将面积比转换为线段比的新的关系，证法更加巧妙灵活.

4 运用等积代换作图

运用等积代换的方法，可以按照题目的要求，作一个m边形，使它和已知n边形的面积相等.

例7作一个四边形，使它和已知的五边形面积相等.

已知：五边形ABCDE（如图8），求作一个四边形，使它和五边形ABCDE面积相等.

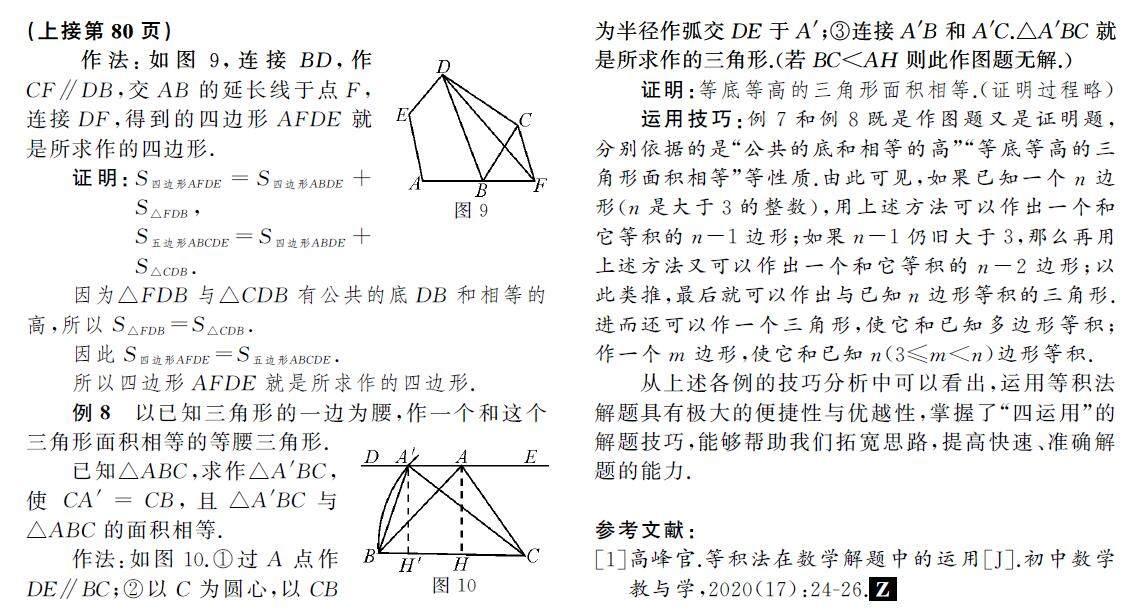
作法：如图9，连接BD，作CF∥DB，交AB的延长线于点F，连接DF，得到的四边形AFDE就是所求作的四边形.

证明：S四边形AFDE=S四边形ABDE+S△FDB，

S五边形ABCDE=S四边形ABDE+S△CDB .

因为△FDB与△CDB有公共的底DB和相等的高，所以S△FDB=S△CDB.

因此S四边形AFDE=S五边形ABCDE.

所以四边形AFDE就是所求作的四边形.

例8以已知三角形的一边为腰，作一个和这个三角形面积相等的等腰三角形.

已知△ABC，求作△A′BC，使CA′=CB，且△A′BC与△ABC的面积相等.

作法：如图10.①过A点作DE∥BC；②以C为圆心，以CB为半径作弧交DE于A′；③连接A′B和A′C.△A′BC就是所求作的三角形.（若BC

证明：等底等高的三角形面积相等.（证明过程略）

运用技巧：例7和例8既是作图题又是证明题，分别依据的是“公共的底和相等的高”“等底等高的三角形面积相等”等性质.由此可见，如果已知一个n边形（n是大于3的整数），用上述方法可以作出一个和它等积的n-1边形；如果n-1仍旧大于3，那么再用上述方法又可以作出一个和它等积的n-2边形；以此类推，最后就可以作出与已知n边形等积的三角形.进而还可以作一个三角形，使它和已知多边形等积；作一个m边形，使它和已知n（3≤m

从上述各例的技巧分析中可以看出，运用等积法解题具有极大的便捷性与优越性，掌握了“四运用”的解题技巧，能够帮助我们拓宽思路，提高快速、准确解题的能力.

参考文献：

[1]高峰官.等积法在数学解题中的运用[J].初中数学教与学，2020（17）：24-26.