融合信息技术的“行星的运动”物理教学

郭雪鹏

20世纪90年代以来，信息技术与课程整合一直是重要的研究课题，信息化、现代化是教育改革的主旋律。然而，教育教学质量并没有得到令人满意的提升。由此引发著名的乔布斯之问——“为什么计算机改变了几乎所有领域，却唯独对学校教育的影响小得令人吃惊？”^[1]究其原因，一是有些教师甚至教育技术专家对信息技术与学科教学深度融合缺乏正确认知;二是有些教师教育观念陈旧，将信息技术视为辅助教学可有可无的工具，认为没有信息技术，教学依然能进行;三是部分教师不了解为什么要进行信息技术与学科教学深度融合，什么是深度融合，如何将信息技术与学科教学深度融合。

一、正确理解信息技术与学科教学深度融合的内涵

信息技术不是可有可无的课堂教学辅助工具，将信息技术融合于学科教学是教育发展和改革的时代要求。教育信息化、现代化是大势所趋。信息技术与学科教学深度融合旨在促进自主、合作与探究等新模式教学，改变长久以来的“满堂灌”教学模式。传统模式下，教师是中心，教师在短时间内向学生单向传授大量知识，效果并不理想：学生的学习主动性丧失，学生的批判性思维和科学思维能力没有得到有效提升。传统模式下培养的学生往往习惯性将教师和专家及教材视为权威，不敢提出反对意见，对问题缺乏独立见解，不敢表达也不会论证自己的观点。信息技术与学科教学深度融合就是要改变这种以教师为中心的课堂教学结构，建立一种同时发挥教师主导作用和体现学生学习主体地位的“主导—主体相结合”的教学结构^[2]。信息技术在学科教学深度融合为自主、合作、探究活动的开展创造了信息化的教学环境。教师应利用信息技术创建教学情境，让学生便捷获取信息和资源进行自主探究和协作学习，发挥其主动性、积极性，最终实现变革传统课堂教学结构的目标^[3]。信息技术与学科教学是否实现了深度融合，关键要看以教师讲授为中心的传统教学结构是否改变，并被“教师主导—学生主体相结合”的新教学结构代替。

信息技术与学科教学深度融合需要大量、类型丰富的数字化教学资源作支撑，助力教师主导作用的发挥和学生自主探究与协作学习。教师既可以从互联网上获取各种资源，也可以自行开发或制作教学资源。以物理学科为例，常用的教学软件有几何画板、仿真物理实验室、Adobe Flash、Algodoo和MATLAB等。网络空间上的资源非常丰富且容易获取，教师应有选择地收集、分类，并将其融入物理课堂教学。同时，教师也要熟练掌握常用软件，具备开发数字化教学资源的能力，不断提高数字化教学能力。

二、应用几何画板探究八大行星的运动规律

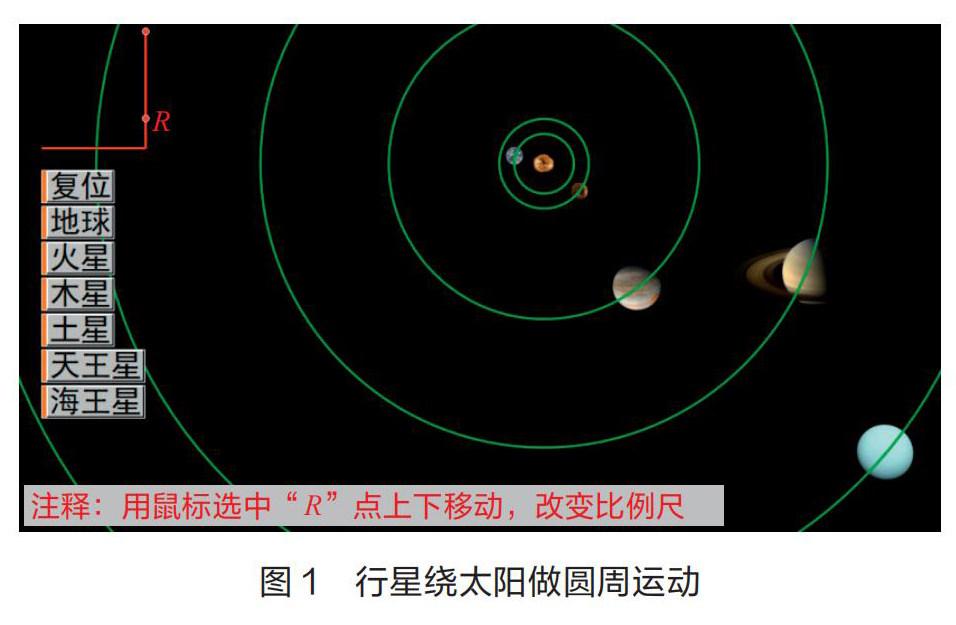
几何画板最初是一款数学软件，现在众多物理教师也将其应用于物理教学^[4]。笔者将结合课例，探讨信息技术与高中物理课堂教学深度融合的路径。八大行星绕太阳近似做匀速圆周运动，行星轨道半径r越大，角速度ω、线速度v、加速度a越小，周期T越大。高一学生初次学习这部分内容时，难以掌握行星圆周运动的这些物理量与半径的关系，不少学生无法利用万有引力定律进行数学推理得到结论。高一学生普遍抽象思维能力和逻辑推理能力不强，解决问题多靠形象思维。如果学生头脑中没有建立生动形象的图景，思维就存在障碍，不能调用已有的知识解决问题。为此，笔者查阅行星轨道半径参数，依据万有引力定律计算得到各行星圆周运动的线速度比值，利用几何画板软件模拟行星的公转运动（如图1），引导学生观察、思考。

人们可以依据各行星到太阳距离的实际数据，计算行星到太阳距离与地球到太阳距离的比值，按照比例确定各行星的轨迹半径。如果操作者用鼠标选中并移动课件中“R”点可以改变地球到太阳距离，各行星到太阳的距离将同步改变。笔者用网络上找到的高清图片表示各行星，生动逼真，能吸引学生的注意力，激发学生探究的好奇心，体现多媒体教学资源开发的艺术性。用户单击图中按钮，行星即绕太阳运动，再次单击，运动停止。这样的课件具有交互功能，便于学生自主操作和探究。建构主义学习理论认为新知识的学习应与学习者已学的知识相互联系，教师应在学生原有知识基础上加以扩充、深化、改造，完成学习者知识结构的更新。依据建构主义理论，笔者设计了如下教学过程。（以下为主要片段）

教师：请大家观察各行星运动快慢，思考线速度和半径有何关系。（教师演示课件）

学生1：行星轨道半径越大，运动得越慢。

教师：“运动得越慢”是指哪个物理量？

学生1：线速度。轨道半径越大，线速度v越小。

教师：轨道半径r越大，周期T如何变化？

学生2：周期T越长。（学生通过课件演示直接观察得到结论）

教师：能从理论上解释为何半径越大周期越长吗？

（学生2无法迁移所学知识解决问题）

教师：行星的轨道半径r和周期T有何定量关系？前面哪一节学习过？

学生（全体）：r³/T²是一个定值。

教师：根据开普勒行星运动的第三定律可知，行星轨道半径越大运动周期越长。

教师：角速度ω与半径有何关系？如何分析？

（停留20秒，留给学生时间思考）

学生3：半径r越大，角速度越小。因为半径r大，根据开普勒第三定律可得其周期T越大。根据ω=      可知，周期越长，角速度越小。

教师：分析得很不错！推理很严谨。如何理解轨道半径r越大线速度v越小？根据v=ωr可以判断出结果吗？

学生4：无法判断。r越大，角速度ω越小，无法判断二者乘积与r的关系。

教师：能定量求解线速度与半径的关系吗？行星做匀速圆周运动，向心力由什么力提供？向心力与线速度、轨道半径有何关系？

学生：太阳对行星的万有引力提供向心力，向心力F_n=m。

教师：请根据万有引力提供向心力，求解线速度的表达式，并分析线速度和行星轨道半径的关系，推导加速度、角速度和周期与轨道半径的定量关系。

笔者用几何画板创设模拟情境引入生动逼真的教学内容，引发学生的好奇心。借助技术工具，笔者模拟行星的运动，引导学生得到行星线速度、周期和轨道半径的关系。笔者通过启发式教学，通过问题链对学生进行启发、提示，引导学生推理分析，使其观察结果建立在严密的逻辑推理上，新内容的学习建立在所学知识基础上，进而发展其科学思维和数理推理能力。

三、信息技术辅助探究行星冲日问题

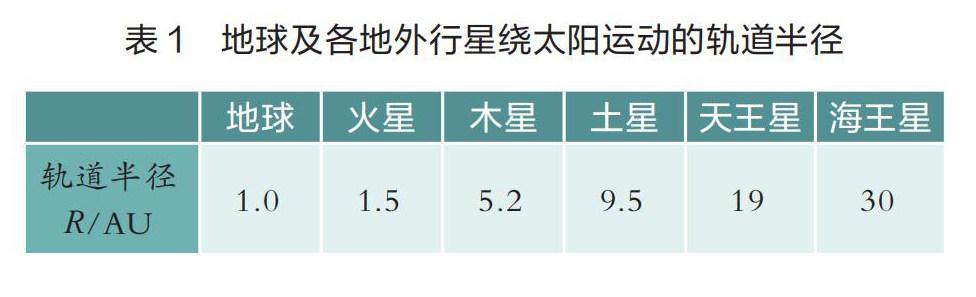
人教版《物理》必修第2册72页第6题：太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到某地外行星和太阳之间，且三者几乎排成一条直线的现象，天文学称为“行星冲日”。已知地球及各地外行星绕太阳运动的轨道半径（见表1），根据题中信息，试计算木星相邻两次冲日的时间间隔，哪颗地外行星相邻两次冲日的时间间隔最短？

审题是解决问题的第一步，学生通过读题、分析题目条件，理解题目情境，建构物理模型。对于纯文本题型，学生审题后应能用示意图重构题目情境，在示意图上标出关键状态、物理量、受力、速度、加速度等信息。不少学生不会解题，原因之一是没有读懂题目，不能用图画表征题目情境，头脑中没有建立情境画面，不能建立动态的情境画面，难以模拟物体的运动情境动画。对于此题，学生解题的困难之一是想象行星的运动图景，在头脑中想象各行星的运动及位置关系。

为引导学生解题，笔者在信息技术支持下开展了如下教学。

教师：请画出第一次木星冲日时，木星、地球和太阳的位置关系。

绝大多数学生能画出木星冲日时三者位置关系。

教师：第一次木星冲日，木星和地球绕太阳做圆周运动，哪颗行星转动得快，哪颗行星转动得慢？请想象不同行星绕太阳运动的动态画面。

很多学生显露茫然的表情，不能判断木星和地球转动快慢，无法建立木星和地球绕太阳转动的动态情境。教师打开制作的几何画板课件，模拟木星冲日。学生观看课件，寻找运动规律。

教师 ：木星和地球绕太阳做匀速圆周运动的角速度相等吗？为什么？

学生：木星的角速度小于地球的角速度。木星轨道半径大，根据开普勒第三定律可知，木星绕日运动的周期大，运动角速度较小。

教师：第二次木星冲日，地球和木星转过的圆心角相等吗？有何关系？

学生1：地球转过的圆心角大。

教师：地球和木星转过的圆心角有何定量关系？

学生1无法解答该问题。教师再次演示模拟动画（如图2）。再次观看后，不少学生观察出地球转过的圆心角与木星转过的圆心角之差为2π，但仍有部分学生无法理解该定量关系。教师安排如下学生分组做模拟实验。

分组实验：学生两人一组，用纸揉成两个大小不同的纸球，分别代表木星和地球;在白纸上画半径不同的两个同心圆，圆心表示太阳，大圆、小圆分别表示木星和地球绕太阳运动的轨道。学生A手持“木星”，学生B手持“地球”。初始时，“木星”“地球”和“太阳”三者共线，且“木星”和“地球”位于“太阳”的同侧。学生B手持“地球”绕“太阳”运动较快，学生A手持“木星”绕“太阳”运动较慢，当“木星”与“地球”再次位于“太阳”同侧且三者共线时，停止运动。

学生分组实验后，教师请两名学生在黑板上模拟木星和地球的运动，演示木星冲日现象，在黑板上记录下两次冲日时地球和木星的位置关系。

设计意图：教师组织学生分组实验，培养学生协作学习意识和合作学习能力。两名学生只有多次磨合，彼此协作才能取得较好的演示效果。学生在模拟活动实验过程可体会、感悟行星运动快慢，总结两次冲日间隔地球和木星转过的圆心角关系。

教师：通过实验，两次木星冲日间隔，大家发现地球和木星转过的圆心角有何关系？

学生2：ω_地t-ω_木t=2π。

教师：题目中没有说明地球和木星的角速度，地球公转周期T_地=1年作为已知量。如何表示上述关系？

学生2：t=2π。根据开普勒第三定律有                 ，解出木星公转周期。

教师：请按照上述思路推导木星冲日的时间间隔表达式。

学生推理得到木星冲日时间间隔表达式，并根据表达式分析发现，行星运动周期越大，两次冲日时间间隔越短，海王星的轨道半径大，周期最大，海王星两次冲日的时间间隔最短。

教师：能提出一个新问题并进行解答吗？

（学生沉默不语，无法提出新的问题。）

教师：两次木星冲日时，木星距离地球最近。（教师加强“最近”两个字的语气）能提出一个类似问题吗？

学生：可以询问第一次木星冲日到下一次木星和地球距离最远时经过的时间间隔。

教师：这是一个不错的问题。请大家画图分析，下一次木星和地球距离最远时两行星转过的圆心角的关系。

学生：地球比木星转过的圆心角多1个π。

部分学生很快看出结果，教师保持沉默，继续让学生画图分析，留给学生时间思索、解决问题。教师使用几何画板（课件）演示从第一次木星冲日到下一次木星和地球距离最远的模拟动画，引导学生观看动画演示，探究木星和地球转过的圆心角关系。学生通过动画知晓，地球和木星距离最远时，二者转过的圆心角相差π，根据圆心角关系求解时间。2分钟后，教师请2名学生将写在纸上的求解过程和结果上交，用交互式电子白板的投屏功能进行投影，分析作答情况。

教师借助几何画板进行动画模拟解决了教学中的难点问题。很多工具既支持教师课堂讲授演示使用，又支持学生在课内外自主探究。仿真实验技术为学生提供自主探究的技术支撑，促进了教与学方式的改进。此课例的教学既体现了教师的课堂引导作用，又彰显了学生的学习主体性，学生在学习中不仅聆听教师讲解，还在教师提示下积极思索，解决问题。

21世纪，教师要培养的是具有创造能力的创新型人才，而信息技术与学科教学深度融合是实现教育教学目标的重要途径。信息技术与学科教学深度融合是提高教师教育教学能力、促进教师专业发展的重要时代机遇。教师是教育改革的践行者，应积极投身于新一轮课程改革，积极探索信息技术与各学科教学深度融合的教学方法和路径，探索有效支持“主导—主体相结合”教学结构的带有教师个人烙印的新型教学方法。

注：本文系安徽省阜阳市2021年教育科学规划课题“信息技术与高中物理教学深度融合的资源开发、路径与教学的实践研究”（课题批准号：FJK21032）的研究成果。

参考文献

[1] 王庆环.“乔布斯之问”问出什么教育问题？[N].光明日报，2015-12-08（14）.

[2] 何克抗.信息技术与学科教学“深度融合”的路径与实现方法[J].中小学数字化教学，2018（2）：17-20.

[3] 何克抗.如何实现信息技术与学科教学的“深度融合”[J].教育研究，2017，38（10）：88-92.

[4] 韩建光.物理深度学习与数字化教学融合的探索与实践[J].中小学数字化教学，2017（3）：8-11.

（作者系安徽省临泉第一中学物理教师）

责任编辑：祝元志