GeoGebra随机模拟法应用案例分析

周建刚　李文东

随机模拟法又称为统计试验方法，是以概率论和统计理论方法为基础的一种计算方法。人们利用随机模拟法可以解决很多概率计算问题，主要步骤如下：将实际问题转化为概率模型，用计算机进行统计模拟，获得问题的近似解。随机事件的概率是一个确定值，但现实中，有些概率不易计算。为解决这一问题，概率统计方法被提出并应用，即借助“大量”试验，以频率估计概率。在一定条件下，重复做n次试验，n_A为n次试验中事件A发生的次数，如果随着n逐渐增大，频率    逐渐稳定在某一数值p附近，则数值p称为事件A在该条件下发生的概率。在课堂上完成“大量”试验不仅费时费力，而且效果不佳。现在，人们应用GeoGebra软件模拟能高效解决这一问题。GeoGebra是自由且跨平台的动态数学软件，载有几何、代数、统计和微积分等功能。为了体现独立重复试验，笔者用GeoGebra产生整数值随机数和均匀随机数的功能，分别执行“区间随机数”和“均匀分布随机数”两个指令，它们分别对应古典概型和几何概型。另外，模拟过程中还需用到“序列”和“条件计数”等指令。下面，笔者以圆周率估计、天气预报、会面问题和曲边梯形面积4个问题为例，阐述如何利用GeoGebra软件进行模拟和运算。

一、用随机模拟法估计圆周率π的近似值

如图1所示，如何利用随机模拟的方法近似计算边长为2的正方形的内切圆面积，并估计π的近似值？

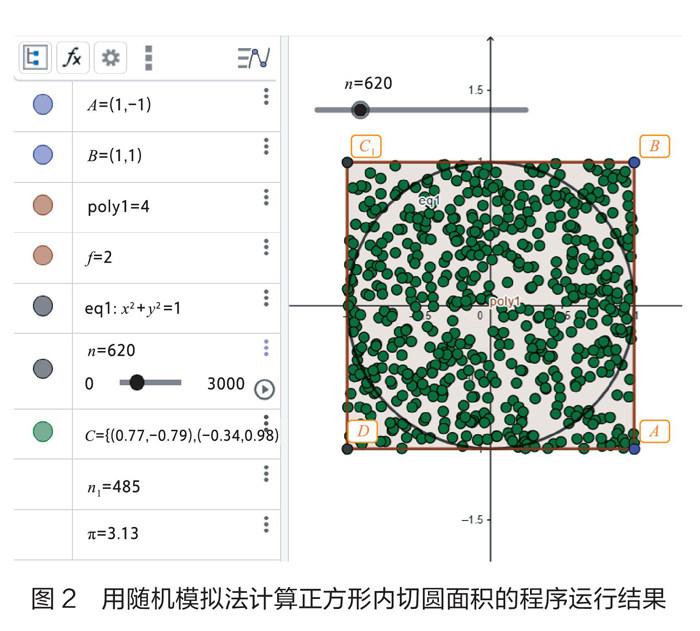
利用GeoGebra模拟的步骤如下。第一步，作正方形及其内切圆：在指令栏内输入“多边形[（1，-1），（1，1），4]”后确认，作出中心在原点且边长为2的正方形;在指令栏内输入“x^2+y^2=1”，作出上述正方形的内切圆。第二步，建立动态参数：单击“参数”工具，设置参数n（撒豆数），最小值0，最大值3000，增量50。第三步，撒豆：在指令栏内输入“序列[（均匀分布随机数（-1，1），均匀分布随机数（-1，1）），i，1，n]”，得到n个有序数对（集合C）。这些点随机出现在正方形内。第四步，计数和估计 ：在指令栏内输入“条件计数[x（i）^2+y（i）^2<1，i，C]”，其值为n₁;输入“4*n₁/n”，即得π的估计值。

上述程序运行结果如下（如图2）。

说明：用“多边形”命令可画出任意正多边形，如输入“多边形[（1，-1），（1，1），5]”可作以A（1，-1）、B（1，1）连线为一边的正五边形。输入随机函数“均匀分布随机数（-1，1）”可产生-1～1的随机数。GeoGebra还有一个“区间随机数[a，b]”，学生可用它产生a～b的随机整数。下面的举例中会用到这一随机函数。

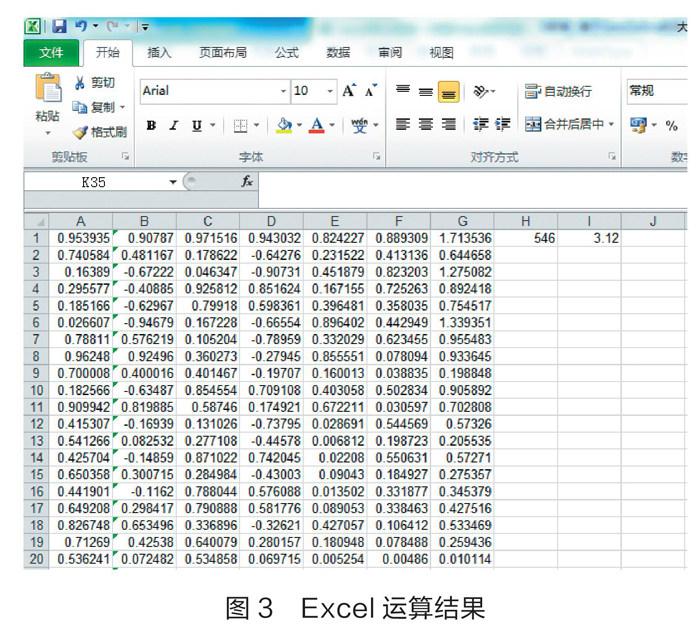
上述过程也可以利用Excel实现。操作步骤如下：第一步，在Excel中选定A1格，输入“=RAND （ ）”，按回车键，产生（0，1）内的随机数，并将A1格复制到A2至A1000，产生1000个（0，1）内的随机数;第二步，在Excel中选定B1格，输入“=2*A1-1”，按回车键，产生（-1，1）内的随机数，并将B1格复制到B2至B1000，产生1000个（-1，1）内的随机数;第三步，在Excel中选定C1格，输入“=B1^2”，按回车键，并将C1格复制到C2至C1000，得到点的横坐标的平方;第四步，在Excel中D、E、F列中重复上述一至三步，得到点的纵坐标的平方;第五步，在Excel中G1格输入“=C1^2+F1^2”，按回车键，并将G1格复制到G2至G1000;第六步，在Excel中H1格输入“=FREQUENCY（G1：G1000，1）”，按回车键，得到1000个点中落入圆x²+y²=1内的个数;第七步，在Excel中I1格输入“=4*H1/1000”，按回车键，得到的数值即为圆周率π的近似值（如图3）。

可见，用Excel操作不仅复杂，而且结果只能以数值显示，不如GeoGebra简便、直观。

二、用随机模拟法估计天气预报下雨的概率

天气预报，今后三天，每一天下雨的概率均为40%。这三天中恰有两天下雨的概率大约是多少？

解题思路：三天中下雨的天数是一个随机变量ζ，它服从二项分布B（3，0.4），因此三天中恰有两天下雨的概率为P（ζ= 2）=C 0.4²×0.6 = 0.288。我们也可以用如下的思路来模拟得到这个概率的近似值：产生0～9这10个随机数字，用0，1，2，3，表示下雨，用4，5，6，7，8，9表示不下雨，这样可以体现下雨的概率是40%。时间为3天，以每3个随机数作为1组，产生三位数的随机数，则这个三位数中恰有2个数字小于等于3代表恰有两天下雨的情况。

笔者带领学生利用GeoGebra进行模拟，步骤如下。第一步，点击工具栏建立滑动条n，用于控制试验次数，设置总次数为3000。第二步，建立含有n个样本点的样本空间A，每个样本点（x，y，z）中的变量为区间[0，9]内的随机整数，指令：A=序列[（区间随机数[0，9]，区间随机数[0，9]，区间随机数[0，9]），m，1，n]。第三步，完成数据统计，输出样本点中恰有2个变量不超过3的频数，指令：a=条件计数[（（x（m）≤3）∧（y（m）≤3）∧（z（m）>3））∨（（x（m）≤3）∧（y（m）>3）∧（z（m）≤3））∨（（x（m）>3）∧（y（m）≤3）∧（z（m）≤3）），m，A]。第四步，频率计算，指令：p=a/n。

上述程序运行结果如下（如图4）。

三、用随机模拟法估计会面的概率

假设小明家订了一份报纸，送报人可能在6：30～7：30将报纸送到小明家，小明的父亲离开家去工作的时间在7：00～8：00，则小明的父亲在离开家前收到报纸的概率是多少？

解题思路：这是一道典型的几何概型的题目。设送报人到达的时间为x，小明爸爸离家去工作的时间为y，记小明爸爸离家前能得到报纸为事件A。以横坐标表示报纸送到时间，以纵坐标表示小明爸爸离家时间，建立平面直角坐标系。小明爸爸离家前能得到报纸的事件构成区域如图5所示。随机试验落在方形区域内任何一点有同等可能性，符合几何概型的条件。只要点落到阴影部分，就表示小明爸爸在离开家前能得到报纸，即事件A发生，所以p（A） =    =0.875。

笔者让学生借助GeoGebra进行模拟，步骤如下。第一步，建立滑动条n，用于控制试验次数，指令：n=滑动条[0，3000]。第二步，建立含有n个样本点的样本空间A，指令：A=序列[（均匀分布随机数[6.5，7.5]，均匀分布随机数[7，8]），m，1，n]。第三步，完成数据统计，输出样本点中满足y≥x的频数，即小明父亲离家时间晚于送报人送报时间，指令：a=条件计数[y（m）≥x（m），m，A]。第四步，频率计算，指令：p=a/n。

上述程序运行结果如下（如图6）。

四、用随机模拟法估算曲边梯形的面积

如何利用随机模拟的方法计算y=1与y=x²所围成部分的面积？

解题思路：应用定积分的知识，计算y=1与y=x²所围成的部分的面积，即

GeoGebra模拟步骤如下。第一步，建立滑动条n，用于控制试验次数，指令：n=滑动条[0，3000]。第二步，建立含有n个样本点的样本空间A。每个样本点落在以A（-1，0）、B（-1，1）、C（1，1）、D（1，0）为顶点的矩形区域内，指令：A= 序列[（均匀分布随机数[-1，1]，均匀分布随机数[0，1]），m，1，n]。第三步，完成数据统计，输出落在阴影区域内点的频数，指令：a=条件计数[y（m）≥x（m）^2，m，A]。第四步，数值计算：矩形面积为2，a/n是随机点落在阴影区域的频率，二者乘积即为所求，指令：S=2a/n。

上述程序运行结果如下（如图7）。

上述模拟方法的优点是不需要编程，教师在指令栏内输入相应的指令（可在右下角的“指令说明”列表中双击获得）即可演示。这种模拟的直观性体现在随机点的数形同步上，即数显示在代数区的“集合A”中，形显示在绘图区中。应用GeoGebra进行计算机随机模拟试验，这种方法易于掌握，操作步骤简单。教师拖动滑动条，可以动态演示随着试验次数增加试验结果的变化情况，这是用计算器等工具无法实现的。在笔者的引导下，学生应用GeoGebra进行数学探索，热情高涨。学生应用GeoGebra模拟运算，不仅加深了他们对于问题本身和解决问题的思想方法的理解，而且在探究过程中获得很好的体验，他们的观察能力、动手能力和探究能力都得以提高。

注：本文系2020年度广东省教育研究院中小学数学研究专项课题“基于数学建模素养导向的高中数学教学实践研究”（编号：GDJY-2020-A-s124）和广东省中山市2020年度教育科研课题“新课标下高中生数学建模核心素养培养的实践与探究”（编号：B2020141）的阶段性研究成果。

责任编辑：祝元志