不规则复杂超限高层建筑抗震性能研究

窦本洋

宣城职业技术学院技工教育管理处， 安徽宣城，242000

中国处于环太平洋与亚欧大陆的地震带之间，受到太平洋、亚欧大陆和印度洋三大板块的挤压，是一个地震灾害频发的国家[1-3]。虽然地震灾害具有不可抗拒性，但人们对地震进行针对性防治，最大程度地降低地震带来的经济损失与建筑破坏[4-5]。控制地震对建筑物和设施的破坏，对中国城市化进程有着重要的影响[6]。高层建筑抗震研究工作也变得非常迫切，使得高层抗震设计已逐渐成了一门学科[7]。以往的抗震设计主要是为了让建筑物保持一定程度的延性、刚性以及强度，但是抗震性能仍然难以保证[8]。我国自改革开放以来，不计其数的超高、超限的建筑拔地而起，高层建筑往往形状各异，具有个性化特征[9]。如何保证这些不规则的高层建筑具有足够的抗震性，并且怎样应用抗震措施和设定抗震目标，目前并无统一的标准[10]。本次研究旨在探讨不规则复杂超限高层建筑抗震性能的一种设计方法，以最大程度地控制地震对高层建筑的破坏。

1 抗震性能设计方法及内容

1.1 抗震性能设计方法

目前，抗震性能设计的主要方法包括能量法、位移法和承载力法三种[11]。其中，位移法属于一种较为接近真实地震状态下结构变化状态的设计方法，但是该方法目前应用较少，但在长期看来，具有一定发展空间。位移法是将位移设定为设计全过程的起点，将位移控制在一定范围内，确保结构能够达到设计要求，再对层间位移等因素进行控制，从而使结构设计达到预期要求。能量法属于一种相对较难掌握的方法，但是该方法精度较高，优点较多。例如，可精确估计结构的耗能，得出哪种构件可能会受到损坏，同时估算出设计结构的破损程度，以便对消耗能量较大的构件进行优化设计。能量法同时也存在一定的缺点，例如，该方法本身较为复杂，面对复杂而多样的地震，参数设计和能量计算并未形成统一的标准。

承载力法是全球应用最多的方法，同样也是我国现阶段明确规范使用的设计方法[12]。该方法的设计理念为：首先，应用弹性法进行常遇地震；其次，通过振型分解反应谱法和剪力法对底部剪力进行计算；再次，通过规范分配至结构中，其中载荷组合方法为分项系数法；最后，设计结构强度，保证结构的变形能力可以达到规范的要求。而在一些不规则、超高等特殊复杂结构中，还需要进一步分析结构的弹塑性。对设计结构采用适合其自身的分析方法，优势是已经实现设防地震效果的结构，还要进行特殊地震下的弹塑性层间变形验算，避免以后由于薄弱部位变形而引起构件的损坏。承载力法主要是理解起来较为简单，并且实践应用也相对简单，能够准备的设计一部分构件，同时分析结构的非线性静力，保证结构设计可以达到要求。但也存在一些缺点，由于承载力法属于弹性计算方法，计算非弹性时，只是简单的折减参数，会降低设计的精度。

1.2 抗震性能设计内容

抗震性能化设计先要确定设防类别，再确定性能目标，最后确定适合的设计指标，也就是确定构件在各种地震动水准中的状态。在设计抗震性能时，要考虑结构的类型、功能的特殊性、投资、场地、修复和损失等因素，综合选择设计的指标，并确定性能目标，优化结构的关键部位。一般情况下，结构抗震目标分为三个水准和两个阶段；而抗震性能目标则包括四个等级和五个水准。其中，各个性能目标均能够对应一组在规定地震地面运动下的结构抗震性能水准。结构抗震性能目标设计表，结构整体遭遇地震后的预期损坏状况及继续使用的可能性统计表以及常用公式表[13-14]。

在对活荷载进行计算时，通常只对地震、风力和楼面进行考虑，对于年限在50年以内的设计，可将荷载效应分为5种情况。一是无地震作用组合，荷载效应组合设计值S，如(1)式所示。

S=γGSGK+ψQγQSQk+ψwγwSwk

(1)

其中，γG表示永久荷载分项系数；γQ表示楼面活荷载分项系数；γw表示风荷载分项系数；SGK表示永久荷载效应标准值；SQk表示楼面活荷载效应标准值；Swk表示风荷载效应标准值；ψQ表示楼面活荷载组合值系数；ψw表示风荷载组合值系数。

二是有地震作用组合，根据规范要求，效应计算参数采用地表70年超越概率63%的地震动参数[15]。荷载效应组合设计值S，如(2)式所示。

S=γGSGE+γEhSEhk+ψwγwSwk

(2)

其中，γG表示重力荷载分项系数；γEh表示水平地震作用分项系数；SGE表示重力荷载作用代表值的效应；SEhk表示水平地震作用代表值的效应。

三是设防地震作用下结构不屈服的地震作用组合，根据规范要求，效应计算参数采用地表70年超越概率10%的地震动参数[16]。若只对水平地震作用进行考虑，荷载组合如(3)式所示。

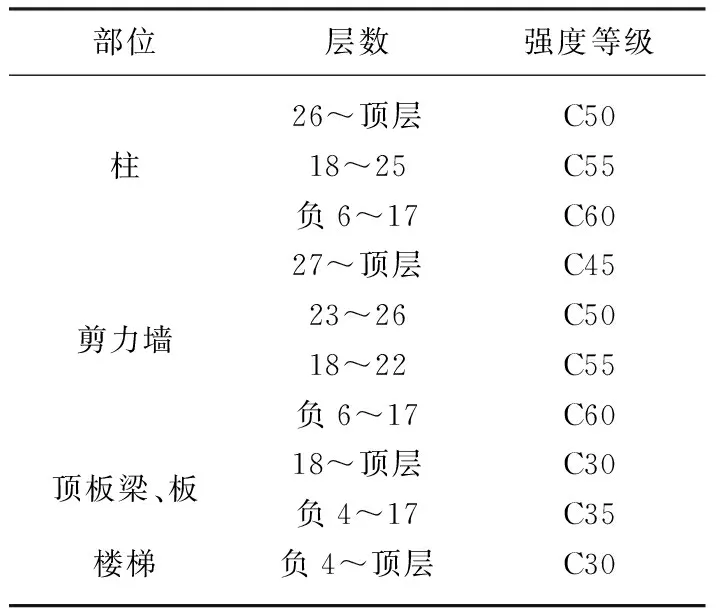
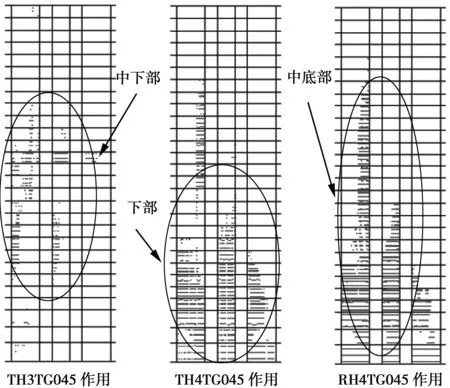
SGK+SEhk

(3)

其中，Rk表示未考虑分项系数的抗力标准值。

四是防地震作用下结构弹性的地震作用组合，根据规范要求，效应计算参数采用地表70年超越概率10%的地震动参数[17]。若只对水平地震作用进行考虑，荷载组合如(4)式所示。

γGSGK+γEhSEhk

(4)

其中，R表示考虑分项系数的抗力设计值。

五是罕遇地震作用下的地震组合，根据规范要求，罕遇地震效应计算参数采用地表70年超越概率2%的地震动参数[18]。在分析弹塑性时，只需对材料的非线性进行考虑，不必调整结构的地震内力情况，荷载组合式与(3)式相同。

2 某不规则复杂超限高层结构的案例概况

该工程项目位于B市D区，有地上、地下两部分，地上部分包括办公楼、酒店和商业性建筑，地下部分则主要为车库。该办公楼是一栋不规则三角形状的超限高建筑，地上部分工程的效果图，如图1所示。办公楼主体高116.8 m，共有30层，建筑面积为51 203 m2，主楼不设裙房，整体为框架核心筒结构，核心筒内包括了机房、楼梯和电梯。办公楼各楼层的构件尺寸随着楼层数的增加而减少。根据受力与功能的不同，核心筒剪力墙厚度通常在300～800 mm之间。该工程属于剪力墙核心筒结构和全现浇钢筋混凝土框架，并且比较规则，按照50年的使用年限进行综合考虑，重要系数γ0=1.0，安全等级设定为二级。此次工程在剪力墙与框架柱之间设了主梁，并在主梁间设了次梁，可较好的使楼板厚度得到降低，同时使地震对建筑物的破坏程度降低，使得建筑物的整体造价最优。

图1 该工程项目地上部分的构成效果图

50年使用年限的基本风压为0.45 kN/m2，基本雪压为0.4 kN/m2，地面粗糙类别为B类。屋面活荷载的不上人屋面载荷为0.5 kN/m2，上人屋面载荷为2.0 kN/m2，栏杆荷载为1.0 kN/m2，施工堆载为4.0 kN/m2，室外地面荷载为5.0 kN/m2。本次工程的混凝土选择情况如表1所示，在钢筋的选择上，主受力钢筋选择HRB400级钢筋，室内和室外型钢分别采用Q345B和Q345C，采用HPB300作为主要的分布钢筋与箍筋。

工程抗震设计中最为重要的依据是地震动参数，依据我国建筑相关规定，拟建办公楼的抗震类别必须为标准设防类[19-20]。地震动参数可以采用不

表1 本次工程的混凝土选择情况

同地震水准抗震的参数，小震规范谱、中震弹性、中震不屈服和大震的阻尼比分别为0.05、0.05、0.06和0.07；连梁刚度折减分别为0.5、0.5、0.4和0.3；周期折减分别为0.9、0.9、0.95和1；地震影响系数最值αmax分别为0.16、0.45、0.45和0.9；特征周期Tg分别为0.45、0.45、0.45和0.5。依据《高层建筑混凝土结构技术规程》中的要求，B级高度结构扭转位移比应小于1.4。而本项目首层的结构扭转位移比值为1.42，其相应层间位移角为1/4 693，并在允许的误差范围2%以内。所以，可以看作符合要求。

3 不规则复杂超限高层建筑结构的抗震性能设计

3.1 超限高层建筑结构分析方法

本研究对不规则复杂超限高层建筑结构的抗震性能设计，首先，确定了模型为主体地上部分；其次，选择软件ETABS与SATWE；最后，选择地震入射角和地震波参数。对于地下室的构造，若首层与下一层存在不小于2的等效侧向刚度比值时，地上主体嵌固可以采用地下室的顶板。通过运算可以得到等效侧向刚度比，通过嵌固层验算后，得到地下一层X、Y侧向刚度分别为2.353 2×108kN/m、2.242 7×108kN/m；地上一层分别为0.986 1×108kN/m、0.984 8×107kN/m；地下/地上分别为2.39、2.28。

地上与地下在不同侧向的刚度均大于2，地上主体嵌固可以采用地下室的顶板，将主体地上的部分作为本次研究的分析模型。此次研究借助ETABS与SATWE对结构模型进行计算分析，采用扭转耦联振型分解法计算结构抗震，同时考虑到偶然偏心的影响和双向地震作用，应用SATWE校验分析计算过程及结果。图形输出时，采用EPDA&PUSH模块分析其动力与静力弹塑性。结构受到不同地震波的作用，其分析结果会存在很大的差异，结果甚至差别十多倍[21]。依据《建筑抗震设计规范》相关规定，分别选取人工波RH4TG045，天然波TH4TG045、TH3TG045，特征周期均为0.45。其中，TH3TG045为加州克恩县1952年7月21日发生的7.7级地震，震源深度16 km，峰值加速度175.9 cm/s2，持续时间20 s；TH4TG045为圣费尔南多1971年2月9日发生的6.4级地震，震源深度13 km，峰值加速度204.8 cm/s2，持续时间20 s；人工波RH4TG045的峰值加速度100 cm/s2，持续时间20 s。

3.2 多遇地震作用下的静力分析

根据ETABS与SATWE自振周期分析情况可知，在0度与41度入射角下自振周期的结果大致相同，振型质量系数均不低于90%，满足对比需求。周期比可以体现出结构的扭转效应，结构扭转受到控制结构周期比的控制，以避免形成过大的结构扭曲，而造成结构的损坏。周期比如(5)式所示。

(5)

扭转周期比不大于0.85，满足设计要求。扭转周期比的运算信息，SATWE的Tt/T1为0°/0.83、41°/0.83，T1、T2的扭转成分分别为0、0.06；ETABS的Tt/T1为0°/0.8、41°/0.81。结构常规设计中最为重要的参数之一为层间位移角，此次研究的结构形式为框架-核心筒，依据《建筑抗震设计规范》相关要求[22]，验算结构的抗震变形时，在罕遇与多遇地震作用下，建筑结构的最大弹塑性层间位移角限值分别为1/100、1/800。层间位移角计算结果，如表2所示。

表2 层间位移角信息

依据《建筑抗震设计规范》相关要求，此次工程的基本周期不大于3.5 s，选取最小剪重比值为0.032。验算结果如表3所示。

表3 结构的剪重比验算信息

由表3可以看出，ETABS与SATWE软件在规范设计下的运算结果相近，且计算结果和剪重比均符合《高层建筑混凝土结构技术规程》的要求。(6)式、(7)式表示钢重比的规定，(6)式、(7)式对于框架核心筒结构应该首先考虑结构整体性能的稳定，对于P-Δ的影响可以忽略。

(6)

(7)

针对本次工程的情况，结构扭转位移比限制应小于1.2。基于规范设计谱下，地震波在0°、41°入射角下的结构扭转位移比，如表4所示。本次研究的结构抗扭刚度较好，符合规范要求。

表4 0°与41°入射角扭转位移比

3.3 地震作用下的应力与墙肢抗剪分析

根据抗震设防要求，墙肢受弯不屈服为主要的中震下的结构加强区，在双向地震和偶然偏心下，墙肢拉应力中震不屈服小于2ftk，不小于ftk的楼层数低于总楼层数的四分之一，若墙肢承受的拉应力不小于ftk时，此时由内置型钢承担全部拉应力[23]。第一层至第三层为本次研究的结构加强区。 对各个主要的墙肢峰值拉应力与在各个楼层出现的拉应力进行计算，如(8)式～(11)式。其中，修正后拉应力表示影响型钢弹性模量的情况，修正前拉应力表示不对影响型钢弹性模量的情况进行考虑[24]。

(8)

(9)

折算面积=墙肢面积+6×型钢面积

(10)

(11)

计算模型反映出了型钢的作用，同时在计算折算面积时也对型钢的作用进行充分考虑，型钢换算成混凝土采用了弹性模量的比值方式[25]。混凝土弹性模量约为型钢的1/6，型钢Q345b的抗拉强度fyk=295 N/mm2，混凝土C60抗拉程度ftk=2.85 N/mm2。修正前后的底部墙体拉应力，要使结构在设防地震作用下的延性、刚度以及墙体抗拉能力得到提升，应在核心筒1至7层将型钢钢骨进入部分主要墙肢内部，以承受中震不屈服的拉应力，忽略钢筋及混凝土的作用，在锚固时充分考虑地下墙体的拉力情况。关于罕遇地震作用下的结构应遵循抗震性能目标进行设计，式(12)表示墙肢截面抗剪能力应满足的要求。

(12)

4 设防地震下不同性能目标的对比

4.1 比较设防地震作用下中震弹性与中震不屈服性能

在设计小震作用下的结构时，应该依据混凝土结构设计的要求调整内力，以使结构的安全得到保障。中震弹性与中震不屈服性能均是设防地震作用下的结构设计，中震弹性设计对荷载分项系数进行了保留，取消内力调整系数，属于常规设计方法；中震不屈服为承载力极限状态设计方法，其去掉了全部的安全度[26]。SATWE模块对中震不屈服、中震弹性和小震弹性进行初始结构设计，再采用SATWE对计算结果进行有限元分析，三种方法的结果对比，如表5所示。

由表5可知，应用三种不同设计方法后，结构总重的计算结果不变；小震位移角符合规定时，对结构采用中震不屈服和弹性分析，位移角的计算结果非常相似，其位移角计算结果大概是小震的2.84倍；中震不屈服计算结果小于中震弹性，表明中震不屈服的设防目标小于中震弹性。

表5 小震、中震弹性、中震不屈服三种方法的结果对比

4.2 基于中震弹性与中震不屈服两种性能目标在大震下的EPDA分析

应用EPDA对动力弹塑性进行分析时，地震波X、Y方向反映某一方向地震波的运算结果，其中X方向表示主方向，同时X方向的运算结果也是层间位移角的主要参考；Y方向表示次方向，主要反映扭转效应的程度。本次研究的结构为特色切三角形，除了对地震动0°、41°的入射角进行考虑外，还应对90°、131°进行考虑。在中震弹性的设防目标下，主方向层间位移角最大的条件为地震波作用方向垂直，中震弹性垂直主方向运算结果显示，波形RH4TG045、TH4TG045和TH3TG045的最大基底剪力分别为99 137 kN、93 208 kN和116 259 kN，最大顶点位移分别为741.5 mm、657.5 mm和580.3 mm，最大层间位移角(1/rad)分别为1/114(22～24)、1/144(15～21)和1/180(23～25)，均值为1/141，最大值为RH4TG045的1/114(22～24)，均达到了抗震的要求。

此时，以4、5号墙体的裂缝出现时刻的最大位移角作为研究对象，对结构的破坏状况进行观察，各个波对4、5号墙体的裂缝分布情况，如图2所示。由图2可知，波形TH3TG045、TH4TG045和RH4TG045作用下的墙体裂缝分别分布于墙体中部、底部、底部和右上部，均达到了抗震的要求。

图2 弹性时不同作用下4、5号墙体裂缝分布图

在中震不屈服大震下的设防目标，主方向层间位移角最大的条件为地震波作用方向垂直，中震不屈服垂直主方向运算结果显示，波形RH4TG045、TH4TG045和TH3TG045的最大基底剪力分别为105 539 kN、95 448 kN和126 359 kN，最大顶点位移分别为726 mm、609 mm和538.5mm，最大层间位移角(1/rad)分别为1/129(21)、1/154(22)和1/195(22～23)，均值为1/155，最大值为RH4TG045的1/129，均达到了抗震的要求。

对结构破坏状况进行观察，各个波对4、5号墙体的裂缝分布情况，如图3所示。由图3可知，波形TH3TG045、TH4TG045和RH4TG045作用下的墙体裂缝分别分布于墙体中下部、下部和中底部，均达到了抗震的要求。

图3 不屈服时不同作用下4、5号墙体裂缝分布图

综上可以得出，应依据计算结果来分析薄弱层的位置。对于中震弹性设计而言，有害层位移角均值是1/328，通过波形计算得出14层有1条，17层有2条，反映出结构薄弱层在中震弹性设防目标下层数是14～17层；对于中震不屈服设计而言，有害层位移角均值是1/212，通过波形计算得出15层，反映出结构薄弱层在中震不屈服设防目标下层数是15层。薄弱层分布在15层及其附近的原因是该层为设备层，具有较大的载荷。对于最大有害层间位移角，中震弹性要小于中震不屈服的位移角，表明了中震弹性具有较小的结构变形。对结构在罕遇地震下进行对比，发现中震弹性对结构的墙体破坏较轻，表明在性能目标中，中震弹性要优于中震不屈服。对于构件要求为强剪弱弯的建筑，抗弯应选择中震不屈服，抗剪应选择中震弹性。

5 结 论

本文就高层建筑抗震性问题，以B市D区的实际项目为例，应用SATWE 、ETABS、EPDA和PUSH软件对该工程在抗震性能化设计进行验证。结果表明，提升结构在设防地震作用下的延性、刚度和墙体抗拉能力，需要在核心筒1至7层将型钢钢骨进入部分主要墙肢内部，以承受中震不屈服的拉应力，充分考虑地下墙体的拉力情况。应用中震不屈服、中震弹性和小震弹性设计方法后，结构总重的计算结果不变；小震位移角符合规定时，对结构采用中震不屈服和弹性分析，位移角计算结果非常相似，其位移角计算结果大概是小震的2.84倍；对于钢筋用量的计算结果，中震不屈服计算结果小于中震弹性；对于中震弹性设计而言，有害层位移角均值是1/328，结构薄弱层在中震弹性设防目标下的层数是14～17层；对于中震不屈服设计而言，有害层位移角均值是1/212，结构薄弱层在中震不屈服设防目标下的层数是15层；对于最大有害层间位移角，中震弹性要小于中震不屈服的位移角，表明了中震弹性具有较小的结构变形。对结构在罕遇地震下进行对比，发现中震弹性对结构的墙体破坏较轻，表明在性能目标中，中震弹性要优于中震不屈服。