具有资产重组和流动性风险公司债券的定价
林建伟 王志焕
(1.莆田学院数学与金融学院,福建莆田 351100;2.华侨大学数学科学学院,福建泉州 362000;3.金融数学福建省高校重点实验室,福建莆田 351100)
1 引 言
公司债券和股票定价问题是金融数学研究的热点问题,其定价的合理性直接决定着发行股票和债券公司的融资成本和公司的经营效率.Merton[1]首次开创了结构化方法,对公司债券和股票进行定价.Merton的工作奠定了公司债券定价研究的基础, 但仍存在信用利差估计偏低的问题.基于Merton的工作,大量文献从不同角度进行推广和改进,Black等[2]提出首次时间通过模型考虑公司债券定价问题;Leland[3]利用结构化方法,通过选取最佳破产边界,完成了永久付息票公司债券的定价;Longstaff 等[4]在随机利率背景下,考虑公司债券定价问题; Zhou[5]在公司资产演化服从跳扩散模型下, 采用随机分析方法对公司债券进行定价; Chen 等[6]在公司资产演化服从双指数跳扩散模型下,采用随机分析方法考虑了永久公司债券定价问题等.但上述文献都假定公司一旦宣布破产,立即被清算,这与实际市场不符合.事实上,破产公司有权申请资产重组保护, 获得一个暂时喘息的机会, 并希望通过资产重组, 使公司摆脱困境.鉴于此, Fan 等[7]首先提出策略债务支付和股票债券互换两种不同资产重组模式,采用结构化方法对于具有无限破产保护期永久公司债券进行定价, Fan等[7]的工作为后来人们研究资产重组公司债券定价问题提供了坚实的基础;Francois等[8]在Fan等[7]工作基础上,采用随机分析理论和方法,考虑了具有有限破产保护期永久公司债券定价问题;林建伟[9]采用偏微分方程方法和结构化方法,推广Francois等[8]模型至考虑公司在有限破产保护期内策略债务支付息票大小;Broadie 等[10]采用二叉树方法,考虑了具有有限破产保护期有限到期日公司债券定价的离散模型;Dai 等[11]通过偏微分方程方法和最优停时技巧,在Broadie 等[10]模型基础上,考虑了相应定价的连续模型;林建伟等[12]采用结构化方法,考虑具有无限破产保护期和有限到期日公司债券定价问题,通过偏微分方程惩罚函数的方法从理论上严格证明了最佳破产边界的存在唯一性和单调性等性质.但上述文献都仅考虑公司的破产风险,而没有考虑公司债券的流动性风险.实际上,流动性是债券市场的生命力所在, 市场的流动性越高, 进行即时交易的成本就越低, 公司的融资成本越低.但市场流动性不足,将使公司增加额外的融资成本,即支付给债券持有者的流动性溢价.Leland 等[13]首次通过滚存风险建立信用风险和流动性风险之间的相关性,基于结构化方法获得了公司债券的定价公式和最佳破产边界,其工作为处理信用风险和流动性风险相关性奠定了坚实的基础,具有开创性意义.不足之处在于模型假定债券二级市场具有充足的流动性,与实际市场不符.He等[14]在Leland 等[13]基础上,通过强度为ξ的Poisson过程来刻画流动性冲击所发生的次数,通过偏微分方程的方法和Laplace变换的技巧,获得了公司债券,股票价值和最佳破产边界的表达式;He等[15]进一步考虑具有内生债券流动性冲击强度ξ相应的公司债券定价问题;Ericsson等[16]在流动性冲击强度服从CIR模型[17]下,考虑了具有流动性风险公司债券的定价问题;周芳等[18]在公司资产价值受宏观市场风险和微观流动性风险影响下,且两种风险因素之间存在相关性条件下,考虑了具有流动性风险因素的风险资产定价问题;Bongaerts等[19]在流动性风险和违约风险相互独立前提下,利用资产定价方法,对具有流动性风险公司债券进行定价,并考察流动性水平和流动性风险关于定价的影响.但上述文献都没有考虑资产重组条款和公司资产的跳跃情形,这与实际不符.事实上,金融市场上常常由于突发事件,自然灾害,重大信息的到来造成公司资产价值的剧烈震荡,单纯的几何布朗运动连续性特征已经不能准确刻画公司资产价值演化过程,而引入跳扩散模型能够更好地刻画公司资产价值的连续性和跳跃性,因此公司资产价值跳扩散特征的准确刻画对于公司债券定价的准确性具有重要意义.同时公司宣布破产时,公司资产重组这一重要条款也是影响公司债券定价的重要因素.
鉴于此,本文拟在He 等[14]的工作的基础上,统一考虑资产跳跃风险、资产重组条款和债券流动性风险这三个重要经济指标对公司债券定价的影响问题.即在公司标的资产服从跳扩散模型下,基于Fan 等[7]提出的股票债券互换资产重组模式,综合采用随机分析的理论方法和结构化方法,考虑具有资产重组和流动性风险的公司债券定价问题,建立相应公司债券和股票定价的数学模型,通过偏微分方程方法和Laplace 变换技巧,获得公司债券和股票定价的显式表达式,以及最佳破产边界解的表达式,并基于定价公式,分析公司资产的跳跃风险、资产重组和流动性风险对定价的影响和所隐含的金融意义.
2 具有资产重组和流动性风险公司债券的定价
2.1 模型基本假设和纳什均衡分配
2.1.1 基本假设
1) 市场无套利和无风险利率为常数r.
2) 在概率测度空间(Ω,F,{Ft}t≥0,Q)上,公司资产价值Vt演化过程服从跳扩散模型

其中δ表示公司总的现金支付比率,σ表示公司资产的波动率,{Zt}t≥0和{ut}t≥0分别表示鞅测度Q下的标准布朗运动和具有强度为λ的Poisson点过程,且假定两者互相独立.
3) 固定债务结构: 公司在任意时刻保持一个连续债券,累积未付本金共P元,累积支付息票每年共C元.构成连续债券中每个单一债券具有相同到期日T,且连续债券中各单一债券到期时间是均匀分布的,即在任意时间段(t,t+dt)上,连续债券的份债券将到期,且需要发行新债券去替换.
4) 新旧债券替换规定: 当连续债券中单一债券到期,公司将发行具有相同到期日和本金的新债券进行替换.新发行债券的市场价格可能高于或低于到期债券的本金,为了保持连续债券的结构,两者产生的盈利或亏损将由公司的股东承担,即若两者差额为正,将直接作为红利支付给股东,但若差额为负,公司将增发股票,通过股票稀释来弥补损失.
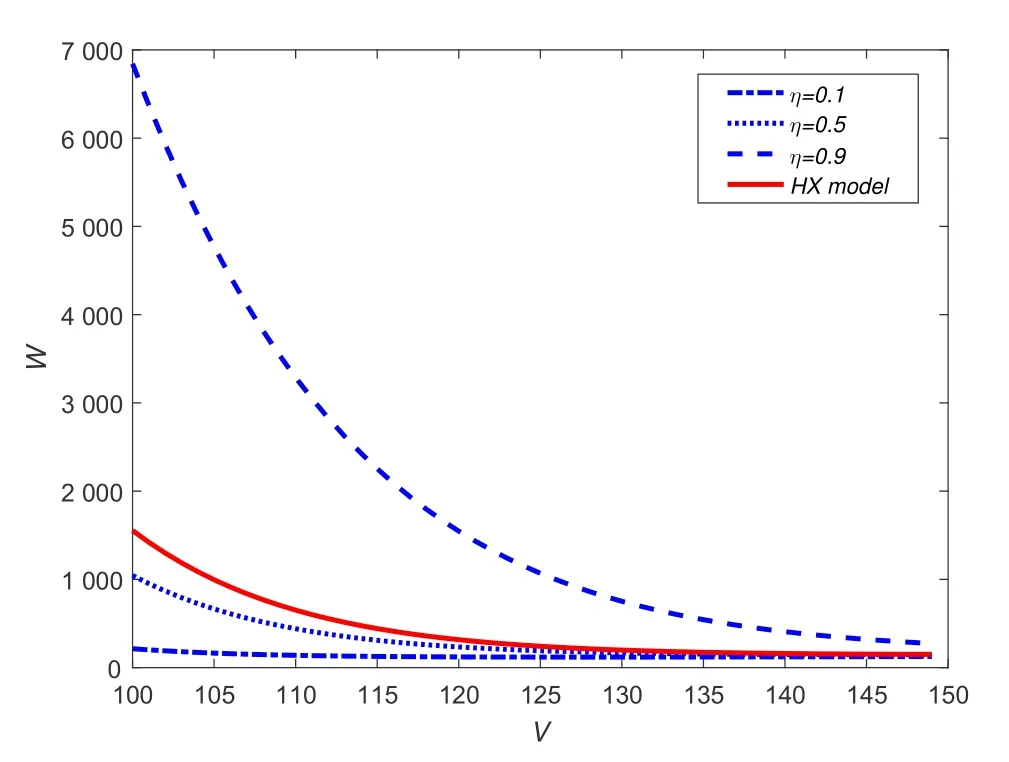
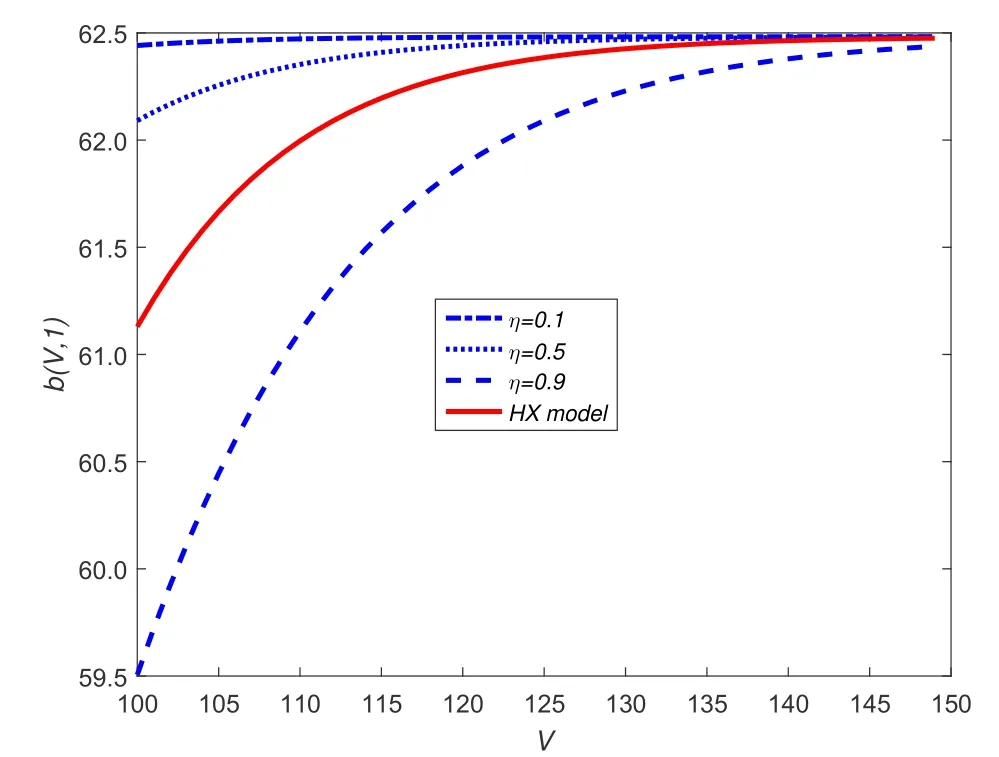
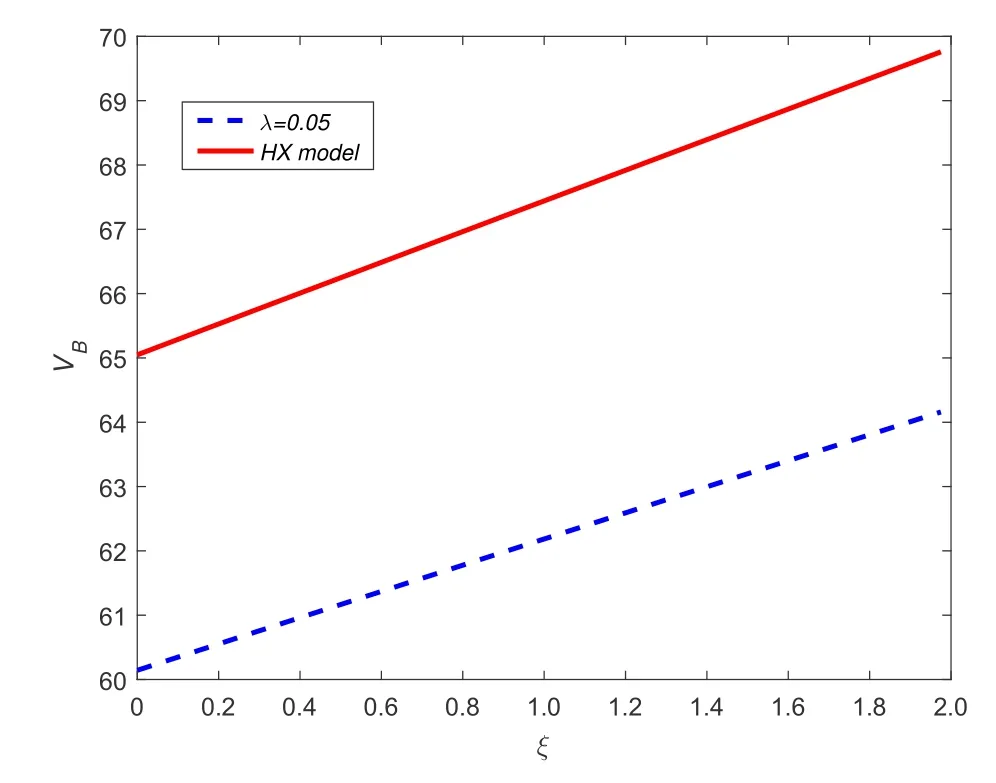
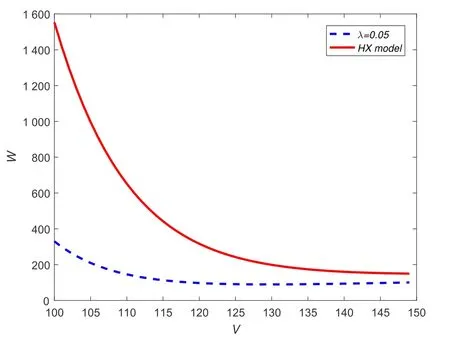
5) 债券流动性风险: 债券持有者面临着债券市场流动性的冲击,冲击时刻通过具有强度为ξ的Poisson点过程{wt}t≥0的跳跃时刻刻画,且假定{wt}t≥0,{Zt}t≥0和{ut}t≥0三者相互独立.当冲击时刻发生时,债券持有者被迫按照市场价的(1−k)比例出售债券合约,这里0 6) 股东按红利获得收益,且最佳破产边界VB通过使得股票价值最大化选取. 7) 税盾收益和清算风险: 公司因发行债券可获得每年税盾收益πC元,这里0<π <1表示税盾比例,但当公司宣布破产时,公司将损失α(0<α<1)比例的资产价值. 8) 资产重组模式—股票债券互换模式(Fan等[7]): 当公司宣布破产时,公司首先将债券等价转化为股票,使得公司成为全股票融资公司,然后向外界投资者出售,获得破产时刻公司的资产价值VB,由此避免直接清算造成的资产损失αVB.最后根据纳什均衡原理对公司的资产价值VB在债权人和股东之间进行重组,并确定债权人和股东相应最佳分配比例. 2.1.2 纳什均衡分配 当公司的资产价值下降触碰到公司的最佳破产边界VB时,公司宣布破产,若公司直接被清算,股票价值将一文不值,债券的价值为(1−α)VB;但是若公司进行资产重组,由基本假设8),债权人和股东按照纳什均衡分配原理对公司的资产价值VB进行重新分配,即 W(VB)=θVB,D(VB)=(1−θ)VB, 其中W(V)和D(V)分别表示股票价值和全部债券价值,θ表示股东的分配比例. 由纳什均衡分配原理,最佳分配比例θ∗确定如下 其中ρ(0 ≤ρ≤1)表示股东的谈判能力.因此,破产时刻股票和债券的价值表示为 W(VB)=αρVB,D(VB)=(1−αρ)VB. 等式(1)右边第一项表示从初始时刻到债券最终停时时刻单位连续债券所获得的息票收益.第二项表示在最终停时时刻单位连续债券价值的贴现值:若发生流动性冲击,按照模型基本假设5)计算单位连续债券价值,债券持有者只能按照市场价的(1−k)比例出售债券合约;若公司宣布破产,公司按照股票债券互换资产重组模式进行资产重组,并依据纳什均衡分配原理,单位连续债券价值为若到期,单位连续债券持有者将获得本金p元. 基于单位连续债券b(Vt,gt),通过动态规划原理和It公式,可得单位连续债券价值b(V,g)满足 对定解问题(P2)进行求解,并返回原变量,有下列结论. 定理1任意给定破产边界VB,单位连续债券价值b(V,g)解的显式表达式表示为 其中 基于单位连续债券价值b(V,g)公式(5),对于任意给定破产边界VB,公司全部债券价值D(V)和单位连续债券的信用利差J能分别表示为 其中R满足如下等式 式(8)右边表示一张具有常数息票c和到期本金p以及贴现率为R的无风险债券的价值. 对于任一公司宣布破产时刻(停时)τB,由上述模型的基本假定4),6)和8),在风险中性测度Q下,股票价值的数学模型描述为 其中T[0,+∞)表示所有破产停时的集合.等式(9)右边第一项表示从初始时刻到停时时刻股东获得的红利收益贴现值.第二项表示为了保持连续债券的结构,任意时间段[t,t+dt]上,新旧债券替换所产生的盈利或亏损[b(Vt,T)−p]dt由公司的股东承担,第三项表示破产时刻,公司通过资产重组获得收益贴现值. 基于公司股票价值W(V)的数学模型(9),通过动态规划原理和It公式,以及结合确定最优破产边界条件–光滑通过条件,可得W(V)满足的自由边界问题为 注意到方程(10)左端含有单位连续债券价值b(V,T),这给自由边界问题(Q1)的求解带来了一定难度,通常的常微分方程的方法无法对其进行求解,借助Laplace变换技巧进行求解,有下列结论. 定理2公司的股票价值W(V)和最佳破产边界VB的表达式分别为 详细的求解过程见附录. 基于公司债券和股票的定价公式(5)和公式(15), 以及最佳破产边界和信用利差表达式(14)和式(7), 通过与He和Xiong(HX)[14]模型1He和Xiong(HX)模型里不考虑公司资产跳跃风险和资产重组条款.比较,分析公司资产跳跃风险和资产重组条款对于公司破产边界和信用利差的影响,以及考察对公司债券和股票价值变化情况.为了方便与HX模型作比较, 选择HX模型里基本参数作为数值计算的基本参数,即:P= 61.68,V0= 100,T= 1,r= 0.08,δ= 0.02,σ= 0.23,C= 6.39,π=0.27,λ=0.05,ξ=1,k=0.01,ρ=0.5,α=0.4. 图1~图4显示当公司资产跳跃强度为零时,相比于HX模型,资产重组条款对于最佳破产边界,股票价值, 公司债券价值和信用利差所造成的影响.图1表明最佳破产边界随着股东谈判因子增大而增大, 但仅当η充分大时,最佳破产边界值才高于HX 模型中的最佳破产边界值.同时,最佳破产边界值关于债券流动性风险单调增加.实际上,在债券流动性风险存在背景下,股东宣布破产时机选择主要权衡两个主要因素:资产重组获益的大小和承担新旧债券替换亏损的大小.特别当η= 0.9时,股东能从资产重组中获得足够多的利益,第一因素起主要作用,因此股东有更强的意愿提前宣布破产而进入重组程序,使得自己权益最大化.此外,由于公司债券流动性风险越大,股东承担新旧债券替换亏损风险增大,股东面临的破产风险增大,因此最佳破产边界值越高. 图1 最佳破产边界VB关于η的变化关系(λ=0)Fig.1 The relationship between optimal bankruptcy boundary VB and η when λ=0 图2和图3表明股票价值随着自身谈判因子增大而增大,但股东和债权人能否借助于资产重组条款获益依赖于自身谈判因子的大小.相比于HX模型,在债券流动性风险存在背景下,股东和债权人往往只能在自身谈判因子充分大时借助于资产重组条款获益.图4表明公司债券的信用利差随着股东谈判因子增大而增大.实际上,当股东谈判因子比较大时,股东有更强意愿提前宣布破产,并借助于资产重组条款来最大化自身的利益,由此导致债权人获得息票收益总和减少,降低了公司债券价值,从而提高了公司债券的信用利差. 图2 股票价值W关于η的变化关系(λ=0)Fig.2 The relationship between equity value W and η when λ=0 图3 债券价值b关于η的变化关系(λ=0)Fig.3 The relationship between debt value b and η when λ=0 图4 信用利差J关于η的变化关系(λ=0)Fig.4 The relationship between credit spread J and η when λ=0 图5~图8显示当资产重组条款不存在,但公司资产存在跳跃风险时,相比于HX模型,公司资产跳跃风险对于最佳破产边界,股票价值,公司债券价值和信用利差所造成的影响.从图5~图8可以看出,相比于HX模型,在公司债券流动性风险存在背景下,公司资产跳跃风险降低了公司的破产风险,降低了公司股票和债券的价值,提高了公司债券的信用利差.实际上,当公司资产存在不稳定的因素比较多时,公司发行的股票和债券对于投资者的吸引度和青睐度减弱,由此导致公司股票和债券的市场价值下降,增大公司债券的信用利差. 图5 最佳破产边界VB关于ξ的变化关系(λ=0.05)Fig.5 The relationship between optimal bankruptcy boundary VB and ξ when λ=0.05 图6 股票价值W关于V 的变化关系(λ=0.05)Fig.6 The relationship between equity value W and V when λ=0.05 图8 信用利差J关于ξ的变化关系(λ=0.05)Fig.8 The relationship between credit spread J and ξ when λ=0.05 在公司资产价值服从跳扩散模型下,基于Fan等[7]提出股票债券互换资产重组模式,综合运用随机分析理论和结构化方法考虑具有资产重组和流动性风险公司债券定价问题,刻画了公司债券和股票价值定价的数学模型,并通过偏微分方程的方法和Laplace 变换技巧,获得了公司债券和股票定价解的显式表达式,以及最佳破产边界解的解析表达式. 附录 定理2的求解过程: 对方程(16)两边取Laplace变换,可得 根据Laplace变换的性质,以及结合边界条件(17)和边界条件(19),可得 由此可得 进一步化简可得 其中η,γ为如下方程的两根,即 且满足η=z −a>1和γ=a+z >0,这里 利用b(V,T)的表达式(5),进一步整理可得 由此可得 记M(x;w,a+w,q)=−K(x;w,q), M(x;w,o,a+w)=K(x;w,o),则 由此可得 另外,容易计算 根据定解条件(18), 可知当x →+∞时,W(x)关于ex线性增长, 又由于η >1和γ >0, 可得当x →+∞时, 式子(23)中eηx项的系数必须为零,即 记 式(24)进一步简化为 由此即可求得最佳破产边界VB的表达式(14). 最后,综合式(23)和式(24),并返回原变量V,可得到W(V)的表达式(15). 证毕.
2.2 单位连续债券价值定价







2.3 公司股票价值定价



3 数值分析



4 结束语


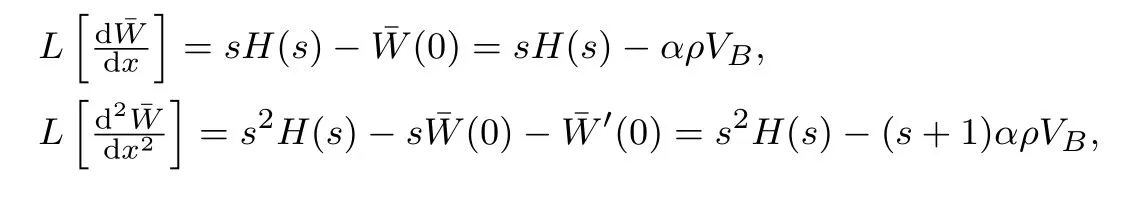
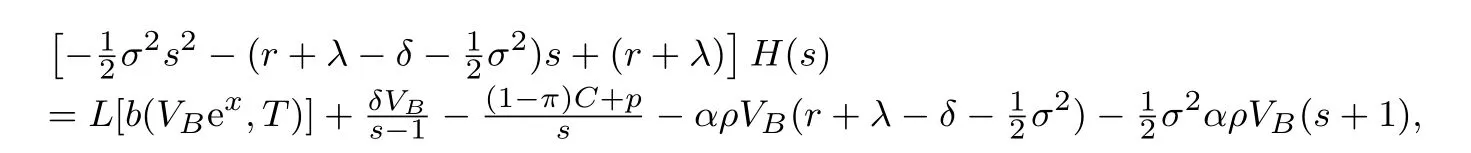


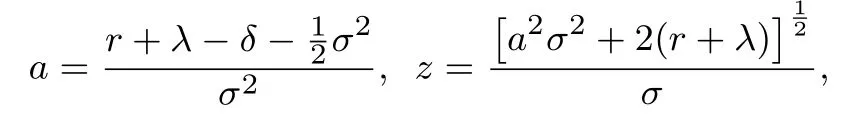
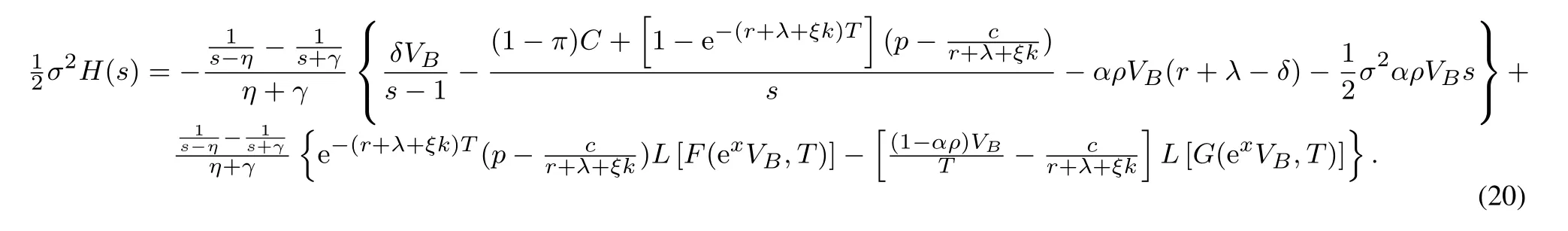







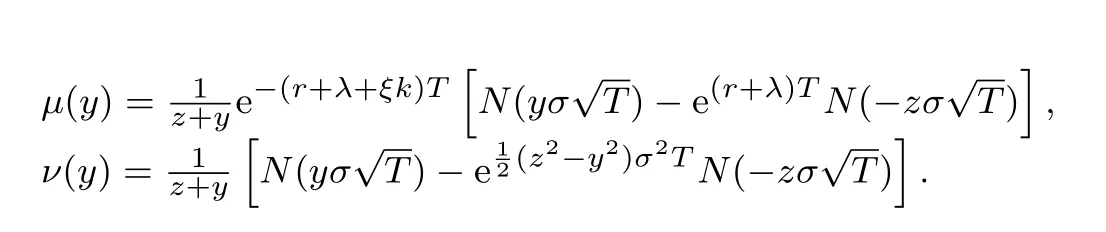
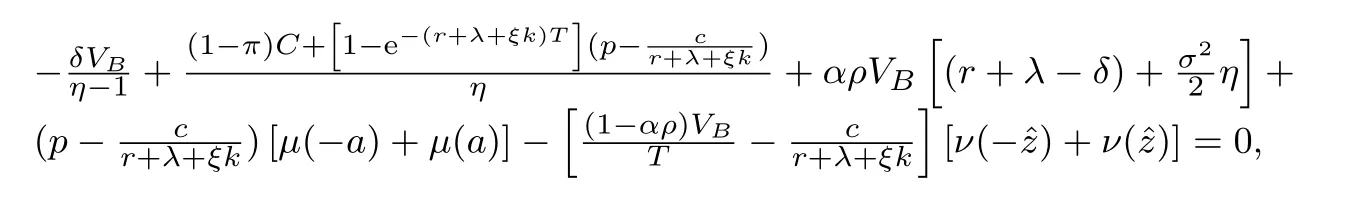
——基于三元VAR-GARCH-BEEK模型的分析

