基于QCSK 的持续噪声式隐蔽传输方案

黄英，万泽含，雷菁，赖恪

（国防科技大学电子科学学院，湖南 长沙 410073）

0 引言

无线通信的迅速发展为人们带来了更加便捷的通信方式。现有的基于密钥的物理层安全技术大多无法应对针对无线信道的新型攻击。因此设计具有无线通信特征的安全通信方式是未来亟须解决的问题。

隐蔽通信，也称作低检测概率（LPD,low probability of detection）通信，是一种可以抵抗第三方监听和审查的通信方式。隐蔽通信允许一方以不违反系统安全策略的方式将信息传送到另一方，实现通信双方的隐蔽信息传输，防止通信信号被恶意窃听者发现，即实现信号隐蔽[1]。若恶意用户无法确认通信信号的存在，则难以实施进一步的非法行为。

噪声式的隐蔽通信作为隐蔽通信实现方案的重要组成部分[2]，其核心思想是利用发射噪声增加Willie 信道的不确定性，从而增加Willie 的检测错误概率。按照方案模型的结构复杂程度，可分为引入额外节点和不含额外节点两类。现有的噪声式隐蔽通信方案设计研究主要集中在人工噪声辅助隐蔽通信的方案和将隐蔽信号调制成噪声形式后再发射的方案。在Bash 等[3]提出平方根法则（SRL,square root law）后，Yan 等[4]根据物理层安全技术中的人工噪声（AN,artificial noise）技术提出了基于人工噪声的隐蔽通信方案并讨论了Willie 的检测性能，之后Yan 团队[5-6]基于香农信息论推导出二元检测下隐蔽通信的相对熵约束，对噪声式隐蔽通信的设计具有指导意义。人工噪声的思想后来又被扩展到引入额外干扰节点或中继节点的隐蔽通信方案[7]，通过增加Willie 检测信道的不确定性获得更高的隐蔽容量。Shahzad[8]将中继转发节点和人工噪声生成节点融为一体，讨论了隐蔽传输的性能。文献[9]则讨论了两跳中继节点下的人工噪声的功率与隐蔽容量的关系。与不含额外节点的隐蔽通信方案相比，引入额外节点的隐蔽通信方案通常具有较好的隐蔽性和隐蔽传输可靠性，但都存在资源消耗大、节点协同要求高、要求发射方知晓Willie 的分布位置等问题。因此对结构相对简单的不含额外节点的隐蔽通信的研究仍在不断推进。

不含额外节点的噪声式隐蔽通信主要采取直接变换噪声式和嵌入式的方法。直接变换噪声式方法将隐蔽信息调制成噪声的形式直接发送，文献[10]讨论了不同相对熵约束下最优的噪声式隐蔽信号分布。仅依赖直接变换噪声的隐蔽通信方案虽然系统结构简单但隐蔽性不强[11-12]。文献[13]利用多天线技术在信道噪声不确定的情形下发射噪声式的隐蔽信号并取得了正的隐蔽通信速率，但采取的穷尽搜索算法需要消耗大量资源。嵌入式方法将噪声形式的隐蔽通信信号嵌入宿主通信系统之中，利用宿主系统解决整个通信系统的同步、信道估计等复杂问题。文献[14]采取污染星座图的方法在正交频分复用（OFDM,orthogonal frequency-division multiplexing）系统中实现了隐蔽通信，但系统实现复杂且无法抵抗监听者的分析。文献[15]提出基于AR模型与联合正态分布构造噪声式隐蔽信号并将隐蔽信号嵌入宿主系统的隐蔽通信方案，这是一种比较成熟的噪声式信号生成方法。但方案中隐蔽信息的传输效率低，并且为了抵抗Willie 的功率检测计，保证隐蔽通信系统的隐蔽性，必须要求隐蔽系统的发射功率远低于宿主系统，导致隐蔽系统的可靠性低。目前嵌入式隐蔽通信面临着低信噪比条件下隐蔽通信可靠性待提高的问题[16]。虽然有研究者利用扩频等方案牺牲有效性来换取可靠性的提升，但由于隐蔽信号发射功率的限制还是无法达到较好的传输可靠性性能，目前对嵌入式的噪声式隐蔽通信的研究仍非常有限。

现有文献针对不含额外节点的嵌入噪声式隐蔽通信方案的研究中，隐蔽通信信噪比极低带来了通信可靠性的不理想。为解决这个问题，本文提出了一种持续发送正交混沌移位键控（QCSK,quadrature chaos shift keying）噪声式信号的隐蔽无线通信方案。Alice 交替发送具有同样功率的隐蔽信息和人工噪声，二者均调制成QCSK 噪声式信号。持续的噪声增加了Willie 信道的不确定性，不变的功率可有效抵抗功率检测；具有噪声特性的隐蔽信号也可以有效抵抗Willie 对信号的进一步分析，较现有方案增强了隐蔽信号的稳键性。本文方案中的系统优化设计在保证宿主系统通信可靠性的前提下，使隐蔽系统在保持隐蔽性的同时能够被分配更多的发射功率，从而提高隐蔽系统的通信可靠性。

1 系统模型

1.1 信道模型

如图1 所示，本文提出了一种新型的基于持续混沌噪声的嵌入式隐蔽通信方案，合法发射机将隐蔽信息调制成混沌形式并与人工噪声交替发送，不变的噪声功率使监听者Willie 无法检测到隐蔽通信行为的发生，从而实现无线网络中的隐蔽通信。本文方案考虑的信道模型为加性白高斯噪声（AWGN,additive white Gaussian noise）信道。系统由一个合法发射机Alice、一个合法接收机Bob和配有功率检测计的监听者Willie组成。其中Alice有发射功率分配设备和两根发射天线，一根用来发射公开信号，称为宿主系统信号；另一根用来选择发射噪声式的隐蔽信号或人工噪声信号。Alice 拥有功率分配器以分配有限的发射功率用于宿主系统传输和隐蔽信息传输。Willie 和Bob 均只有一根天线用来接收信号。本文模型考虑的场景是Alice向合法用户Bob 发送公开消息信号，同时会随机尝试传输隐蔽信息；Willie 试图检测是否有隐蔽信息传输行为发生。

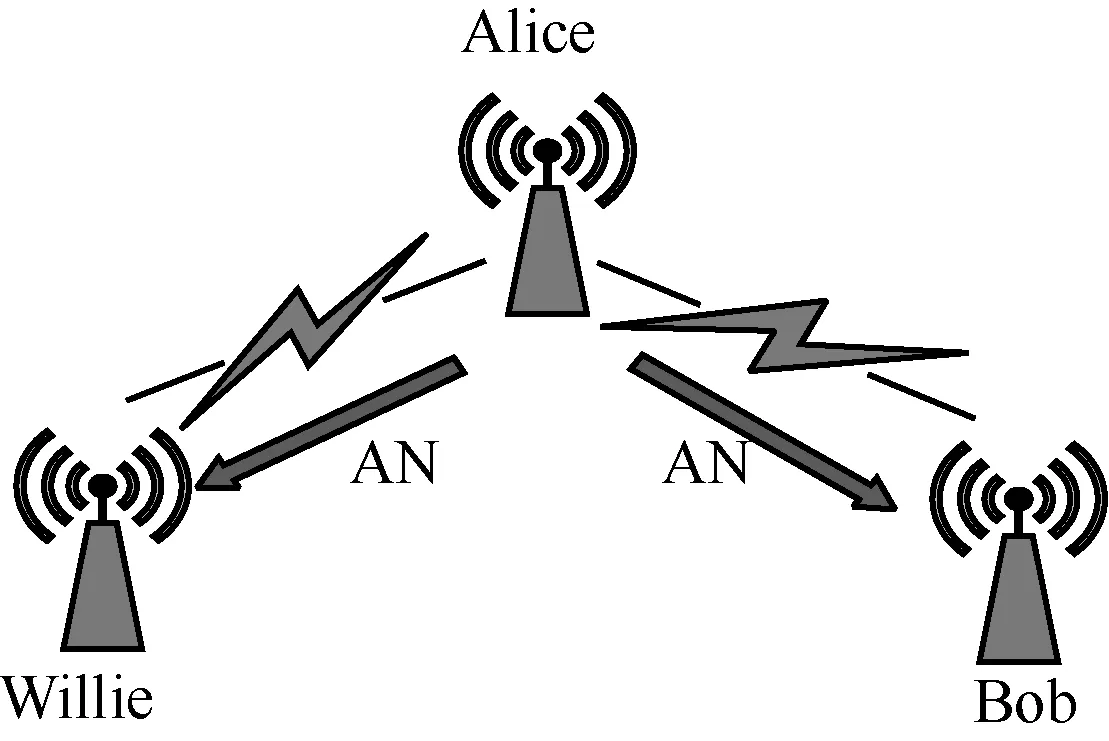
图1 持续噪声式隐蔽传输方案模型

1.2 Willie 的二元检测

Willie 的检测可以看作一个二元检测的过程。零假设H0表示无隐蔽通信行为发生，Alice 发送混沌噪声形式的人工噪声信号；备择假设H1表示有隐蔽通信行为发生，Alice 发送同为混沌噪声形式的隐蔽信号。D0表示Willie 判决没有隐蔽通信行为发生；D1表示Willie 判决有隐蔽通信行为发生。假设Alice 进行隐蔽通信传输和发送人工噪声的概率相等，监听者Willie 的检测性能通常用检测概率PD衡量，则有

其中，ξ=α+β为检测总错误概率，α=PFA≜为虚警概率，为漏检概率。合法通信方的隐蔽性目标通常是无论Willie采取何种检测手段，总有检测概率PD≤ε，其中ε为任意小的正数。

1.3 QCSK 调制

QCSK 是在非相关差分混沌移位键控（DCSK,differential chaos shift keying）系统的基础上提出的调制方案，其利用一组互相正交的混沌基函数在一个符号周期长度中传输2 bit 的信息[16]。

类似于正交移相键控（QPSK,quadrature phase shift keying）调制方式，QCSK 拥有多种星座图样，本文方案中选取的映射关系更利于调制后的信号逼近噪声的特性[17]。映射方式如表1 所示。

表1 映射方式

QCSK 调制后的信号可表示为

其中，Eb为比特能量，T为符号周期。在解调端，将接收信号延时后分段做相关判决即可解出传输的信息比特。QCSK 误比特率计算式为

1.4 混沌映射方案

本文选取改进后的Logistic 映射方案[18]，如式(4)所示。

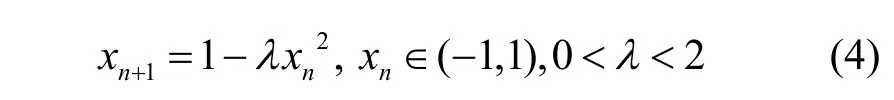
进入满映射状态时，该映射方案具有期望为零、方差恒定的统计特性。

2 持续噪声式隐蔽传输方案

2.1 隐蔽传输方案

本文方案利用持续的噪声信号迷惑Willie，使其无法分辨是否有隐蔽通信行为发生。在发送公开消息的同时，Alice 交替地发送调制成混沌噪声形式的隐蔽信号和人工噪声信号。传输公开消息的系统称为宿主系统，采取QPSK 调制方式。传输隐蔽消息的系统称为隐蔽系统，采取QCSK 调制方式。Alice 将隐蔽信息嵌入宿主信息中进行传输，宿主通信系统解决整个通信系统的同步、信道估计等问题。在合法接收端，Bob 接收机根据收到的含噪信号先解调出宿主信息比特，再利用解调出的宿主信息恢复出不含噪声的宿主系统调制后的符号，进而恢复出隐蔽信息比特。

本文方案整体通信系统框架如图2 所示。

图2 本文方案整体通信系统框架

设i=1,2,3,… ,n表示序列中的第i个符号，xh、xc和xj分别表示Alice 发射的宿主系统信号、隐蔽系统信号和人工噪声信号符号序列，(r=h,c,j)为共轭转置。那么有

假设Alice 的发射功率为Pa，定义功率分配因子μ∈[0,1]表示将一定比例的功率分配给宿主系统，则有

其中，Ph是用于宿主系统的发射功率，Pc是用于隐蔽系统的发射功率。根据模型假设，为抵抗监听者Willie 的能量检测，Alice 应使人工噪声的发射功率Pj与隐蔽信息的发射功率相等。用H0和H1表示Alice 不发射隐蔽信息与发射隐蔽信息时的2 种假设，此时合法接收端Bob 的接收信号yb可表示为

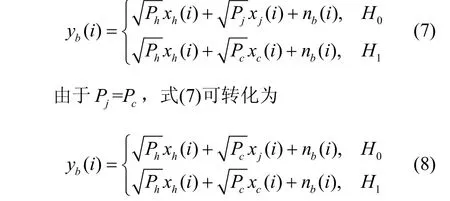
其中，nb是Bob 处的复高斯白噪声信号，并且。类似地，Willie 的接收信号yw可表示为

其中，nw是 Willie 处的复高斯白噪声信号，。由式(9)可得，Willie 的功率检测计无法从能量检测的角度判断是否有隐蔽传输进行。由于xj和xc是具有相同统计分布的混沌噪声信号，故监听者Willie 不论是使用功率检测计还是从时域、频域、统计分布的角度进行分析均无法区分Alice 发送的是无意义的人工噪声还是承载着隐蔽信息的信号。因此本文方案具有强隐蔽性，更进一步地，由于本文方案的隐蔽性主要源于QCSK 混沌和人工噪声方法，因此不需要极低隐蔽系统发射功率的约束，打破了现有嵌入式隐蔽通信方案中隐蔽通信系统必须保持极低发射功率的限制。本文方案利用将隐蔽系统嵌入宿主系统的方式解决了混沌通信系统的同步等关键性问题，系统结构相对简单可行。

2.2 功率分配对宿主系统误码性能的影响

宿主系统的误码性能与其接收机输入信噪比有关。为方便表述，定义系统信噪比、宿主系统信噪比和隐蔽系统信噪比如下。

1) 系统信噪比为总发射功率和总噪声功率之比。

2) 宿主系统信噪比为宿主系统的接收机收到的宿主信号与噪声功率之比。

3) 隐蔽系统信噪比为隐蔽系统的接收机收到的隐蔽信号与噪声功率之比。

假设嵌入隐蔽系统之前QPSK 宿主系统信噪比为γ0，此时系统信噪比也为γ0，即此时γQPSK=γ0，发射功率全部用于QPSK 宿主系统。嵌入隐蔽系统之后由于发射功率配比发生改变，假设信道噪声功率不变，则QPSK 系统信噪比变为

设此时系统信噪比为γ1，为达到相同的QPSK宿主系统误码率（BER,bit error rate），则需要提高系统信噪比γ1使γQPSK=γ0，显然γ1＞γ0。为衡量通信系统嵌入隐蔽发射机后QPSK 的性能损失，定义达到相同误码性能时整个系统的信噪比变化值Δγ为代价指标，即

由式(10)和式(11)可得

整理式(12)可得

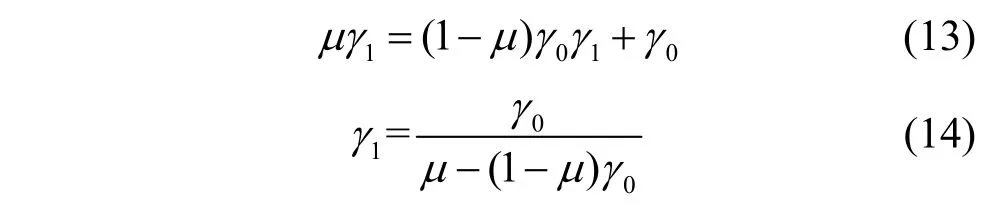
注意，此处需满足

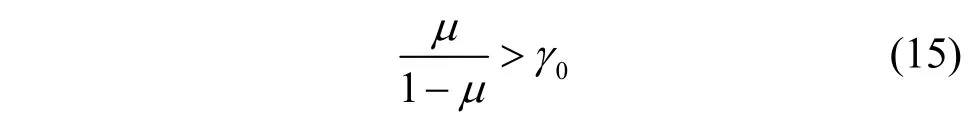
则代价因子可表示为

化为对数形式为

式(17)同样需满足式(15)。由式(17)可得，当μ一定时，γ0越大则QPSK 宿主系统所需要付出的代价越大，这是符合实际情况的。因为当信噪比γ0越大时，QCSK 隐蔽系统所占的功率也相应提升，对QPSK 宿主系统的解调器而言，其包含的输入噪声也同时增加，故达到同样性能所需的系统信噪比需求变高。

2.3 系统优化设计

通信系统可靠性主要由误码率衡量。本文方案中宿主系统采取QPSK 调制方式，宿主系统的误符号率[18]如式(18)所示。

如图2 所示，接收者Bob 在解调信号时需要先恢复宿主系统符号后才能正确解调出隐蔽信息，因此在计算宿主系统误码率时，隐蔽信号将被看作噪声。宿主系统符号信噪比为

QCSK 的解调是通过接收序列的分组相关判决完成的。由于宿主系统的发射功率和隐蔽系统的发射功率存在明显差异，在隐蔽系统接收端，宿主系统误码导致的隐蔽系统异常符号幅度值会明显区别于其他符号，因此可以识别出隐蔽系统的异常符号并直接将其剔除以增加判决精度。假设隐蔽系统传输符号数为N，则无异常符号的符号数为

因此隐蔽系统QCSK 的误比特率为

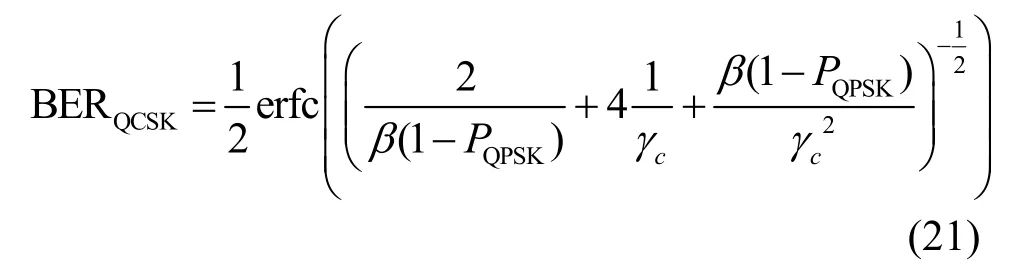
其中，γc为隐蔽系统的比特信噪比。由于恢复出了宿主系统的符号，在隐蔽接收机处可以将宿主信号抵消掉。由此进一步得到隐蔽系统符号信噪比为

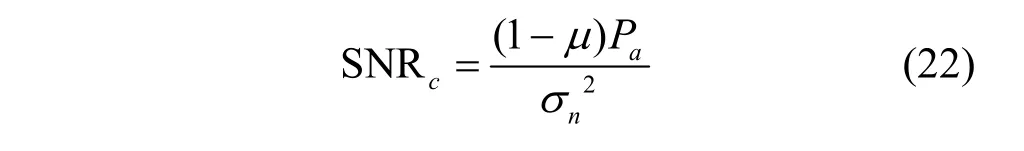
由于erfc 函数是单调减函数，因此当Alice 可以用于发射信号的总发射功率Pa和信道噪声功率一定时，对于要求的隐蔽系统误码率Pce，总有上界μhb使隐蔽系统满足需求误码率。

采取QPSK 调制方式的宿主系统误码率只与宿主系统接收机输入信噪比有关。即在发射功率和信道噪声功率一定时，宿主系统误码率只与功率分配因子μ有关，对于QPSK 宿主系统来讲，功率分配因子μ越大，误码率性能越好。通过合理地选取功率分配因子，可以使宿主系统付出的代价满足合法通信双方所能承受的要求。采取QCSK 调制方式的隐蔽通信系统误码率则只与功率分配因子μ和混沌扩展因子β有关。由于通信还需要尽可能提高有效性，对于隐蔽系统来讲，固然是希望μ越小越好。因此，对于要求的宿主系统误码率性能（或宿主系统允许的最大损耗代价 Δmax）和隐蔽系统误码性能约束下，有如下最优化问题

求解最优化的步骤如下。

1) 寻找μ的下界μmin，保证QPSK 宿主系统的误码满足合法接收者所能承受的最大代价 Δmax。

2) 在μ的取值域[μmin,1]中任意取μ，均可满足宿主系统的最低性能要求，此时可得到隐蔽系统误码率最小时的β取值βopt和μ取值μopt。

3 系统隐蔽性能分析

3.1 基于相对熵的隐蔽性分析

不失一般性地，假设监听者Willie 不知道合法通信方的先验知识。对于二元检测，为使检测错误概率达到最小值ξ*，Willie 所采取的最优的检测方式为能量检测法，则有

其中，VT(p0(y w),p1(yw))为全变分距离。其上界可用相对熵表示为

其中，p0(yw)和p1(yw)分别为Willie 接收信号yw在H0和H1下的似然函数。

由式(9)所知，Alice 发送或不发送隐蔽信息时Willie 接收信号的区别仅在于xi和xj的分布的区别。由于xi和xj均经过QCSK 调制，因此当序列足够长时，二者趋于同一个分布。设fAN(xi)和fcov(xi)分别为发送人工噪声和隐蔽信号时发送信号的概率密度，则有

即有无隐蔽通信发生时Willie 端接收信号的相对熵可表示为

此处应注意，如式(9)所示，Willie 端的接收信号由宿主系统的QPSK 信号、混沌噪声与高斯噪声叠加而成，叠加信号后的概率密度表达式较复杂。在式(27)中求解H0与H1下Willie 接收信号分布时，并不容易写出概率密度函数与分布函数的闭式形式，但根据本文方案模型，在有无隐蔽通信行为时Willie 端接收信号的区别仅在于AN 信号和隐蔽信号的不同。故可近似地根据Alice 发送信号的概率分布求解Willie 接收信号的相对熵。当码长趋于无穷时，Willie 端接收信号的相对熵趋近于0，Willie的检测错误概率趋近于1。因此Willie 无法有效检测是否发送隐蔽信号，本文方案具有强隐蔽性。

3.2 基于接收序列相似度的隐蔽性分析

由于在3.1 节Willie 接收信号相对熵的求解中无法根据先验概率分布得到简洁的相对熵表达式，只采用了近似表示并求取极限。因此在本节根据Willie 接收端的后验知识评价方案隐蔽性。欧氏距离常用来衡量多维空间中2 个点的绝对距离。本节采用基于欧氏距离的准则衡量H0与H1下Willie 接收信号序列Yw0与Yw1的相似程度。欧氏距离计算式为

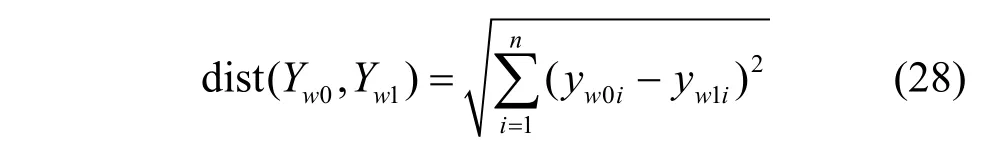
接收矢量间距离越小，表示接收矢量越相似，隐蔽性越强。由于Willie 使用辐射计进行能量检测，当序列样值之间的欧氏距离小于其检测器门限η时，Willie 无法将2 个序列区分出来。因此，接收信号相似度κ10为

3.3 基于多尺度分析的隐蔽性分析

假设监听者Willie 具有一定的分析能力，即在考虑检测成本的基础上，除去常规的在时域或者频域分析是否有隐蔽传输行为发生外，Willie 会尝试截取一段接收信号ywk进行分析以判断是否有隐蔽信息的传输。考虑假设Willie 使用多分辨率分析（MRA,multi-resolution analysis）进行信号中分量的分析

如式(30)所示，经典的Mallat 算法通过把一个任意信号分解成高频细节部分Wi和低频轮廓部分Vi，不断地迭代取出低频分量做进一步的分解，可以在不同尺度上提取出信号的精细分量和粗略分量，有效区分不同信号。

对于本文方案而言，由于交替发送的人工噪声信号和隐蔽信号有着相同的时频特征，因此Willie 也无法通过时频分析检测出是否存在隐蔽信息的传输。

4 性能仿真与分析

下面，通过仿真实验来验证所得隐蔽性结论并进一步分析本文方案的性能。仿真参数如下：宿主系统采取QPSK 调制方式，隐蔽系统采取QCSK 调制方式，隐蔽系统比特数为1 000，QCSK 扩展因子β=64。

不同信噪比下有无隐蔽信息传输时的时域波形和频谱对比分别如图3 和图4 所示。由于本文方案设计的噪声式传输信号与人工噪声信号具有一致的统计分布和信号功率，在不同信噪比下，除去信道噪声引起的毛刺外，在有无隐蔽信号传输时Willie 的接收信号都极为相似，Willie 无法通过观测某个时隙中的信号波形和频谱判断是否有隐蔽传输行为发生。因此Willie 无法根据其观测数据设定有效的判决准则，只能采取随机猜测的方法，证明了本文方案的强隐蔽性。

图3 不同信噪比下有无隐蔽信息传输时的时域波形对比

图4 不同信噪比下有无隐蔽信息传输时的频谱对比

不同信噪比下有无隐蔽信息传输时星座图对比如图5 所示。如果Willie 截取一段接收信号进行分析得到其星座图，该星座图随着系统信噪比变化始终呈现出在宿主系统星座点周围遍布噪声的形式。Willie 从星座图案中只能获取到公开的宿主消息，无法区分是否有隐蔽通信发生。本文方案仍能保持极好的隐蔽性能。

图5 不同信噪比下有无隐蔽信息传输时星座图对比

图6 为对比隐蔽信息和AN 信号的差异性。被分析的信号被设计成前时长为隐蔽信息，后时长为AN 信号的样式。对其进行MRA 发现，尽管MRA 可以提取信号的精细分量与轮廓分量，但仍无法区分该信号前后两部分的不同分量。这是因为在本文方案设计时，AN 信号的选取与隐蔽信号的统计分布一致且AN 信号和隐蔽信号功率相等，从而保证了强隐蔽性。

综上所述，本文方案不仅可以抵抗监听者Willie 的功率检测，从图3～图6 可以看出，监听者Willie 不论是从时域、频域或是小波MRA 的角度均无法判别是否有隐蔽通信行为发生。这说明面对具有一定分析能力的监听者Willie 时，本文方案仍具有强隐蔽性，Willie 则无法区分是否有隐蔽通信发生。这证明本文方案具有内生的抗检测性能。

图6 接收信号多分辨率分析结果

图7 对比了不同μ下Willie 接收信号的相似度。从图7 可以看到，随着信噪比的增加，接收信号的相似度增长并趋近于1；当分配给隐蔽系统的功率越少时，接收信号相似度越高，但总体趋势上都趋近于1。这表明低信噪比时导致信号相似度低的原因不是信号本身隐蔽性的降低，而是信道噪声功率较大引起的信号幅度波动，这样的噪声幅值波动同样会导致Willie 的功率检测计失去作用，本文方案仍能达到合法通信方的隐蔽性传输目标。这证明了本文方案的强隐蔽性。

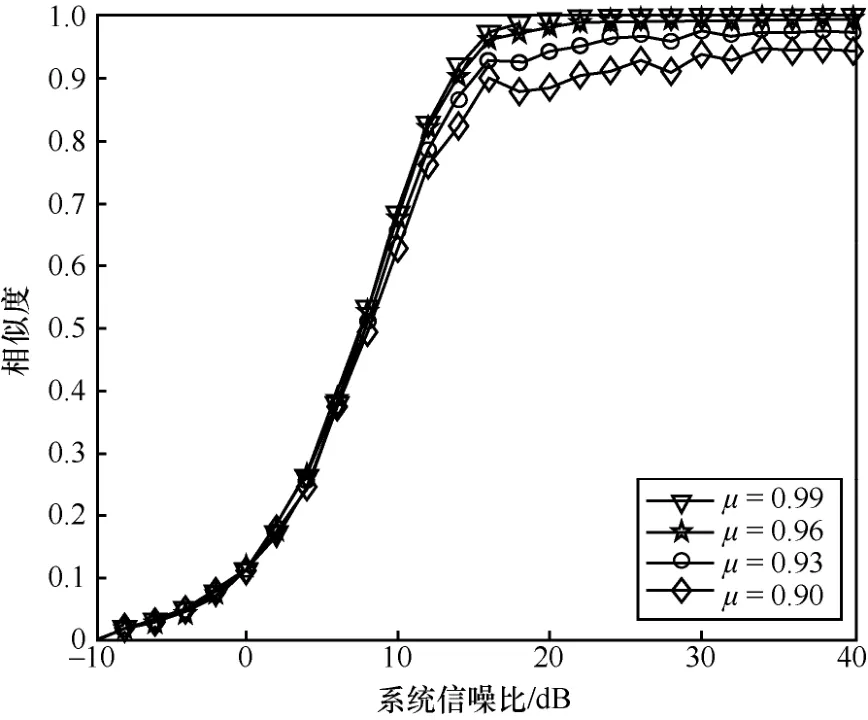
图7 不同μ 下Willie 接收信号的相似度

假设要求QPSK 宿主系统在整体系统信噪比为15 dB 时误码率能达到1×10-4，并且此时宿主系统代价损失不超过2 dB。根据式(30)取μ=0.99，βopt=64，此时宿主系统代价为1.7 dB，误码率曲线如图8 和图9 所示。

图8 宿主系统和隐蔽系统误码率曲线

图9 宿主系统误码率曲线对比

本文方案由于具有强隐蔽性，故不存在现有方案中隐蔽系统发射功率必须保持远小于宿主系统发射功率的限制，可以适当增加隐蔽系统的发射功率以提升隐蔽系统的性能。

由图8 可知，当系统信噪比大于12 dB 时，本文方案的隐蔽系统误码率开始明显低于文献[15]方案，并随着系统信噪比的增大误码率急剧下降；当系统信噪比为21 dB 时，本文方案已经比文献[15]方案低2 个数量级。对宿主系统而言，当系统信噪比为15 dB 时，宿主系统的代价损失仅为1.7 dB；当宿主系统误码达到1×10-7时，隐蔽系统误码率比文献[15]方案低2 个数量级，隐蔽系统可靠性远优于文献[15]方案。经分析得，文献[15]方案为保证隐蔽性，隐蔽系统信噪比需比宿主系统低30 dB，导致其接收机信噪比极低。事实上，由于系统方案的隐蔽性不强，文献[15]方案中隐蔽系统信噪比必须低于宿主系统30 dB 并不是因为隐蔽系统的发射功率增加会使宿主系统的传输立刻急剧恶化，而是为了保证隐蔽传输的隐蔽性。而实际上宿主系统的传输是可以容忍一定程度的代价损耗的，因此本文方案在保证隐蔽性的前提下，通过合理设计宿主系统和隐蔽系统的功率分配，可以将更多的发射功率分给隐蔽系统，换取更高的隐蔽系统的性能。

由图9 可知，本文方案和文献[15]方案中宿主系统的误码率曲线十分接近，证明本文方案在已有方案的基础上维持了宿主系统的误码性能，并且大幅提升了隐蔽系统的可靠性。

5 结束语

为提高嵌入式隐蔽通信的通信可靠性，本文在噪声式隐蔽通信的场景下，研究改进的嵌入式隐蔽通信方案。该方案基于QCSK 将隐蔽信息调制成混沌噪声的形式并与人工噪声信号交替发送，实现了强隐蔽性的隐蔽通信；在保证隐蔽性要求前提的基础上，突破了现有方案中隐蔽系统功率必须保持极低的限制，发射机可以分配给隐蔽系统更多发射功率。通过优化设计发射功率分配方案，在对宿主影响代价可接受的范围内既保证了宿主系统的可靠性又提高了隐蔽系统的可靠性，为解决嵌入式隐蔽通信中隐蔽信息的可靠传输问题提供了解决方案。