基于节理不确定性的可靠度分析——以西藏某岩质边坡为例

胡 康，任光明，常文娟，李征征，邹林志

（1.地质灾害防治与地质环境保护国家重点实验室（成都理工大学），四川 成都 610059；2.中国电建集团西北勘测设计研究院有限公司，陕西 西安 710065）

0 引言

随着对边坡研究的深入，可靠度分析已成为结构和岩土工程师日渐关注的课题[1]。在边坡参数的不确定性和变异性影响下，传统的单一安全系数并不能很好地解决工程实际问题，其中边坡功能函数形式的高度非线性以及隐含性是时常遇到的难题。对此，学者们研究使用了可以表达明确物理意义的失效概率的可靠度分析方法[2−5]。节理发育是岩质边坡工程上的难题，岩体中的节理分布对岩石边坡稳定性有着重要影响，国内外学者在节理边坡稳定性评价上取得了不少成果[6−9]。陈国良等[10]介绍节理现场测量方法和常见的节理分布统计概型，并基于蒙托卡罗法进行三维节理网络计算机模拟；王宏等[11]对岩石中节理的生成技术进行探讨，并证明岩石力学网络技术前景广阔；严豪等[12]基于Voronoi模型对碎裂岩质边坡进行了节理有限元分析；李源亮等[13]简要介绍节理网络模型原理及方法，并以实际案例进行稳定性评价。节理网络模型为研究节理边坡提供了有效方法，在此基础上，肖术等[14]通过赞比亚某边坡将节理网络与点估计法结合起来，以岩体强度参数为输入参数进行了稳定性评价；张宜杰等[15]利用Baecher 模型对JEF-PEM 方法进一步研究，评估边坡的失稳概率与破坏机理；国外学者Przewlocki 等[16]也通过点估计法，以边坡材料强度指标为输入变量，对某海崖边坡进行了可靠度分析。

部分学者对边坡节理发育带来的不确定性影响进行相应研究。许湘华等[17]建立以节理倾向、倾角和间距为随机变量的边坡可靠性模型，采用蒙托卡罗法产生符合随机变量分布类型的随机数，进行边坡可靠度分析；王双等[18]用蒙托卡罗法对服从Fisher 分布的节理产状进行模拟，得到安全系数的分布规律和边坡可靠度；王双[19]针对产状分组和边坡不确定性分析，提出了新的产状椭圆对称分布概率模型并结合到EM 算法；申矫健[20]在广义Hoek-Brown 理论基础上，通过区间理论与敏感性分析理论对岩体参数的区间取值，得出更好地反映工程实际的安全系数区间值。

综合学者们的研究成果，作者发现节理带来的不确定性对边坡工程影响重大，具有研究意义，而采用PEM 法评估可靠度，并不局限于边坡自身强度参数作为输入变量，节理强度参数同样对边坡稳定性具有较高敏感性。因此，文章基于节理的不确定性，提出了以节理强度参数为输入变量的节理边坡可靠度分析方法。

1 基本原理及模拟步骤

1.1 Baecher 节理网络模型

Baecher 模型是1978年由Baecher[21]提出，具有操作简单快捷、算法灵活、与研究区实际情况相似度高的特点。模型中假设节理具有有限的迹长，迹长、产状、密度等遵循一定的统计规律，且结构面每一个中心点在空间上以泊松点过程分布[22]。为了避免模型区域的边界效应，Baecher 算法通过扩大区域，再生成节点，最后用原边界区域对网络进行剪切生成模型（图1）。该模型主要通过两种方法来定义：一种是Fisher 函数分布法；另一种是指定Dip/Direction 的方法。一般来说，Fisher分布更适合定义节理网络，因为无论节理空间分布情况如何，通过平均倾角/倾向、费舍尔常数K 和标准偏差都能准确定义。而Dip/Direction 法，当平均倾角/倾向接近象限临界值时，便不能正确地定义所需的方向分布。

图1 Baecher 节理网络模型Fig.1 Baecher joint network model

Cacas 等[23]、Dershowitz 等[24]提出Fisher 分布具有较好的拟合性。在空间上，其裂隙面的倾角用法线的方向表示，而一组裂隙面的法向量将围绕其代表法线和向量呈现Fisher 概率函数分布，即

式中：f(θ）——概率密度函数；

θ——均值向量的角标准偏差；

K—Fisher 常数，又称散度因子，代表结构面产状的离散程度，K值越小，则结构面产状越离散。

1.2 PEM 方法原理

PEM 方法是基于Rosenbluth[25]提出的一种统计矩方法，又称点估计法。该方法利用随机变量的平均值和方差计算功能函数的有限估计点函数值及其相应加权值，再求和得出状态函数的一阶矩、二阶矩等，进而评价边坡的可靠度。

对于一般的边坡稳定性问题，其状态函数可定义为

式中：Z——边坡稳定性系数；

x1,x2,···,xn——容重、泊松比、黏聚力、内摩擦角等随机变量。

在已知n个随机变量（x1,x2,···,xn）的平均值 µxi和标准差 σxi，且不清楚随机变量xi(i=1,2,···,n)的分布函数的条件下，则在区间(xmin,xmax)上分别对称地选择2 个取值点，一般按均值 µxi的一个正负标准差 σxi取值，即：

对于影响节理岩体稳定性的n个变量，当在均值±σ 对称取值时，有2n个取值点，所有可能的组合有2n个。可根据相关程序计算出2n个稳定系数，并可计算出稳定性系数Z的平均值和标准差。

若输入随机变量彼此独立，且各组合发生的概率相等，那么Z的均值点估计为：

标准差的点估计为：

在假定输入随机变量符合正态分布的基础上，可靠性指标β 可表示为：

最终可得到边坡破坏概率为:

2 边坡工程地质条件及参数取值

2.1 边坡基本特征

文章研究边坡属于易贡藏布干流某拟建水电站的库区边坡，河谷狭窄，岸坡陡峻，平均海拔约3 150 m，上下游宽约1 285 m，前缘河流流向约NE68°，河水位高程约3 085 m。该边坡呈整体上略向河床突出的弧形坡体，坡向约NE64°，横向平均宽度约1 200 m，轴线方向长约1 920 m，出露面积约3.1 km2。模拟选取剖面位于边坡中部轴线附近，分布高程3 085～4 680 m，前、后缘高差约1 595 m，总体上坡度较陡，变化范围不大，约42°，靠近顶部分水岭分布平均坡度约18°的缓坡带。该边坡属于大型工程边坡，对库区下游居民安全和水电站正常运行至关重要。

2.2 边坡结构特征及参数取值

库区岩石组成主要为白垩系细粒二长花岗岩，钻孔揭露深度约85～90 m，为弱风化花岗岩，深于90 m 为正常花岗岩。据平硐统计资料，边坡深部基岩的中、缓倾结构面发育较少，而陡倾结构面发育较多。

统计数据表明，边坡平硐内共统计有结构面裂隙444 条，按走向其优势结构面分为：①NNW 组，所占比例为36.94%；②NNE 组，所占比例为15.32%；③NE 组，所占比例为13.06%，为缓倾结构面；④NW 组，所占比例为10.36%，典型出露节理如图2所示，节理极点等密度图如图3所示。根据统计的结构面倾向和倾角，易知该岩质边坡节理发育，按风化程度和结构面分布情况，将边坡分为强风化层、弱风化层和微新岩层（图4）。

图2 边坡出露典型节理Fig.2 Exposed typical joints of slope

图4 边坡模拟剖面结构图Fig.4 Simulation model

对取回试样进行室内试验，并结合部分相似花岗岩边坡的参数取值，确定了该边坡各结构区的力学和强度参数，以及结构面的特征值如表1—表3所示。

3 边坡可靠度分析

3.1 敏感性分析

为证明节理发育岩质边坡中节理对边坡稳定性状态有显著影响，对边坡进行敏感性分析，为简化流程，仅选取节理J1 与弱风化层作为对象，以其黏聚力（c）和内摩擦角（φ）强度参数作为随机变量。计算方法与PEM法相似，对每个变量按平均值（xi=µi）与标准差（xi=µi±3σi）取3 个值，每次变化单个变量其余变量取平均值。

据表1—表3 提供的参数，采用Phase2 软件，初步建立节理边坡有限元数值模型，在有限元强度折减法的基础上，采用Mohr-Coulomb 屈服准则，应力条件设定为仅自重应力，约束条件为底部全约束，侧面法向约束，节理末端条件设为在地表“端部张开”，其余设为“端部闭合”，计算结果如表4。

表1 岩体参数取值Table 1 Parameter values of rock mass

表3 结构面强度特征值Table 3 Strength characteristic values of structural plane

表4 敏感性计算结果Table 4 Sensitivity calculation results

以平均值作为计算参数，计算得到边坡稳定性系数为1.35。

将基于每个随机变量取值µi、µi+3σi 和µi−3σi计算的稳定性系数分别表示为FS0、FS1、FS2，并按式α=(FS1−FS2)/FS0计算作为该参数敏感性指标，α 越大，表明该参数对边坡影响越大，计算结果见表5。

表5 敏感性指标计算结果Table 5 Sensitivity index calculation results

计算结果表明，该节理岩质边坡的敏感性：节理强度参数>岩体强度参数，内摩擦角>黏聚力，节理敏感性甚至略大于岩体自身强度因子，证明节理对边坡稳定性具有显著影响。因此下文以节理强度参数c、φ作为边坡可靠度分析输入变量的思路具有可行性。

3.2 PEM 法可靠度计算结果

建立边坡节理有限元模型如图5，根据PEM 方法的计算步骤，首先需要确定作为输入变量的特征参数。为研究岩质边坡节理强度参数的不确定性，将内摩擦角和黏聚力作为输入变量构建点估计概率模型，考虑该边坡中存在的主要节理组（表2），共需要分析3 组节理组6 个随机变量，分别在±σ 处取值，组成26总共64 种组合模式，然后计算它们的稳定性系数，最后根据式（4）、式（5）得出其平均值和标准差，据式（6）、式（7）得出其可靠性指标和破坏概率。

表2 结构面几何特征值Table 2 Geometric characteristc values of structural plane

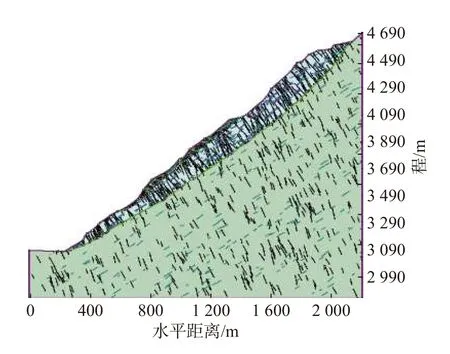
图5 边坡节理有限元模型Fig.5 Finite element model of rock slope joints

计算结果表明，天然状态下的64 组边坡模型基本符合正态分布（图6)，稳定性平均值为1.344，最大值为1.48，最小值为1.23，相比不添加节理的边坡稳定性计算结果1.7，降低了19.7%，说明节理发育对边坡稳定性影响较大。通过点估计法相关计算公式，求得该岩质边坡稳定性系数标准差为0.057 3，变异系数为0.042 6，可靠性指标为6.007，破坏概率为0.001%，表明该边坡可靠度较高，发生失稳破坏的概率极低。

图6 PEM 法计算稳定性系数概率分布图Fig.6 Probability distribution of stability coefficient calculated by PEM method

3.3 节理有限元法计算结果

由图7、图8 可看出，未考虑节理时该边坡在临界状态时产生剪应变较小，主要集中于弱风化带底部以及边坡后缘拉裂区，而考虑节理情况下边坡变形程度相对较大，最大剪应变为0.004，且由于边坡节理在靠坡面发育更为密集的特点，剪应变主要集中在后缘靠坡面的剪切变形区域。

图7 最大剪应变云图（添加节理）Fig.7 Nephogram of maximum shear strain(adding joints)

图8 最大剪应变云图（不添加节理）Fig.8 Nephogram of maximum shear strain (without joints)

图9、图10 对应边坡在添加节理与不添加下的位移矢量图，由图可见，在不添加节理条件下，边坡位移相对较小，且位移矢量分布较分散，顺坡向滑移和竖直方向沉降变形突出，而考虑节理条件下，边坡会产生更大的变形，最大位移量达到5 cm，且在缓倾坡外节理的影响下，顺坡向位移矢量更加突出，表现出更强烈的滑移变形，证明了节理发育对边坡变形破坏的控制性作用。

图9 边坡位移矢量图（添加节理）Fig.9 Slope displacement vector diagram (add joints)

图10 边坡位移矢量图（不添加节理）Fig.10 Slope displacement vector diagram (without joints)

图11 是对应边坡发生的剪切变形模式，可看出边坡的变形受到节理控制，红色箭头为错动方向，灰线为滑移后坡面线，沿结构面方向边坡发生剪切错动，并在坡面产生锯齿状拉裂逢。推测该边坡变形机理为：在自重作用下，边坡有向临空方向发生悬臂梁倾倒的趋势，并沿陡倾坡内节理发生剪切滑移，同时在层间岩体中产生拉张效应，而岩体又发育缓倾坡外节理，因此岩体顺势沿缓倾节理发生剪切错动，产生相应屈服（图12）。

图11 边坡沿节理剪切变形Fig.11 Shear deformation of slope along joints

图12 屈服节理分布图（局部）Fig.12 Distribution of yield joints (local)

综上所述，该节理岩质边坡可能发生以倾倒-滑移为主的变形。因该工程后续施工中仍有开挖过程，形成新的临空条件，所以对该边坡进行研究是有必要的。

3.4 蒙托卡罗法验证结果

蒙特卡罗模拟(MCS)是一种强大的统计分析方法，已成功应用与可靠性分析和风险评估之中，同时也一直被认为是所有方法中最精确的方法[26]。通过具有随机不确定性参数描述的响应函数的概率分布，利用计算机生成假定的概率分布的随机变量来完成，是一种生成重复多次模型，并计算特定条件发生的次数来评价其概率的方法。总而言之，该方法是在统计分析的基础上，得出了模型输出的结论。因此该方法的关键问题是模拟要达到满意的概率精度所需的仿真次数。

利用边坡极限平衡软件Slide，应用MCS 法对边坡可靠性进行验证。采用常规岩体强度参数c、φ值，根据边坡结构分3 层共6 个随机变量进行评价，计算参数见表1，计算次数为10 000 次。计算结果见表6。

表6 可靠度对比分析结果Table 6 Results of reliability comparison analysis

可见两种方法计算结果存在一定差异，但不具有显著性，传统不考虑节理分布的蒙托卡罗法，得到边坡稳定性系数更大为1.590，边坡可靠性指数稍大，边坡破坏概率更小，也表明了节理发育对边坡稳定性有不可忽视的影响。文章采用的以节理强度参数作为输入变量的PEM 法，充分考虑了节理参数的不确定性，对研究该类型的节理边坡有一定的参考价值。

4 结论

（1）节理对该岩质边坡有较高敏感性，节理发育情况直接影响到边坡变形模式及稳定性状况。Baecher网络模型可以灵活模拟边坡节理，是一种有效的分析方法。基于节理参数的不确定性，以节理参数为输入变量的PEM 法评估边坡可靠度是一种可行的方法。

（2）该工程边坡在节理影响下，发生以倾倒-滑移为主的变形，且在后续施工中仍有开挖过程，可能造成边坡稳定性降低，应开展边坡进行位移监测。

（3）PEM 是概率岩土工程应用的有效工具，与MCS相比，它所需要的模拟仿真次数更少，因单次边坡稳定性计算耗时不短，所以较少的仿真次数直接提高了计算的效率。点估计法还有一个重要优点是在可靠性分析中可以忽略特定随机变量的概率密度函数，因此该方法适用于分析各种工程问题。

（4）在天然工况下，两种可靠度评价方法结果具有一致性，该边坡可靠度较高，PEM 法得到边坡可靠性指标为6.007，失稳破坏概率0.001%。