基于图像处理的深孔零件轴线直线度检测方法研究

王浩，郝建军，葛帅帅

（1．重庆理工大学机械工程学院，重庆 400054；2．重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆 400054）

深孔零件的轴线直线度被视为是衡量深孔零件合格与否的一项重要参考指标。根据国家标准GB/T11336-2004《直线度误差检测》，深孔类零件的轴线直线度指的是实际轴心线对其理想轴心线的变动量。直线度误差会影响深孔零件的性能和使用寿命等，因此很有必要对深孔类零部件的轴线直线度进行检测，并将其严格控制在合理的误差范围之内。

近些年来，许多学者针对深孔直线度的检测方法开展了深入研究。孟晓华等作者[1]利用“激光三点法”原理，设计了一种新型的检测深孔零件轴线直线度的装置，该检测方法属于非接触式测量，适用于内径范围在24-51mm的深孔。于大国等作者[2]利用反转法和超声波检测法来对深孔轴线直线度进行测算，并研制了配套装置用于验证假设，实验结果表明该方法能满足一般精度要求。刘新波等作者[3]提出了一种利用单激光束旋转的深孔零件轴线直线度检测方法，该方法依托机床主轴及其进给装置，结构简单，验证结果表明该方法能够对直线度进行在机测量。Pablo Martinez等作者[4]研制出了一种基于图像处理和自动准直原理的几何参数测量仪，能综合测量深孔零件的轴线直线度、圆度和圆柱度。Masayuki等作者[5]设计研制了一套直管内表面的数字全息检测系统，通过比较多色强度图像和管道内表面高度轮廓图，实现直管内壁参数的自动测量。Salah Elfurjani等作者[6]提出了一种检测微孔（直径小于1mm）内径和圆度的新方法，利用旋转金属丝探针和声发射对微孔内表面进行接触式测量，并据此创建三维剖面。上述直线度检测方法多用于检测内孔形面光滑且长度较短的深孔零件，且部分方法数据采集过程比较复杂，检测效率低。然而对于一些采用定心机构来获取内孔截面中心点信息的检测方法，往往忽略了定心机构引入的装配误差。

本文基于图像处理技术，提出了一种光电测量元件外置的深孔零件轴线直线度检测方法，通过搭建视觉测量系统获取零件内孔不同截面图像信息，从而进一步得到截面中心点坐标，并根据坐标变换原理对中心点坐标进行修正，最后利用LSM算法和MATLAB软件计算出直线度。

1 直线度检测系统组成及工作原理

1.1 检测系统组成

本文设计的深孔零件轴线直线度检测系统结构框图如图1所示，其主要由平行激光发生器、自定心机构、CCD相机、计算机等组成。

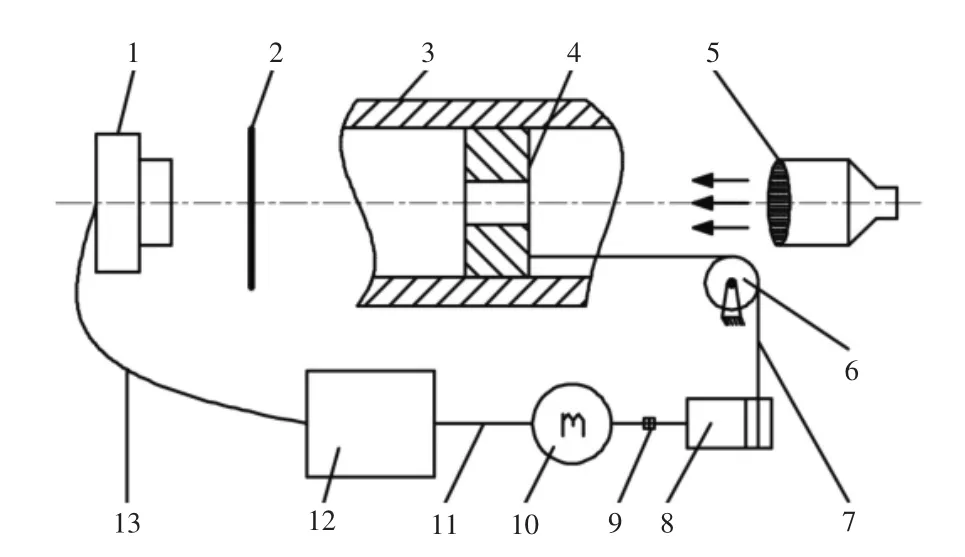
图1 直线度检测系统结构框图

1.2 系统工作原理

检测前，先将定心机构置于深孔零件远离电机那一端，同时将十字形通光孔的指向朝上，作为初始检测位姿，定心机构通过自调节功能实现定心；然后将平行光管产生的平行光垂直照射到十字形通光孔上，由CCD相机接收出射端的十字形光斑。检测过程中，由计算机控制电机使滚筒转动，进而使线绳牵引定心机构在深孔零件内移动。通过设置电机的转速和工作时间，可以使定心机构按照一定的步长移动。最后，利用CCD相机拍摄不同位置下得到的十字形光斑，通过计算机图像处理能够快速准确获取不同截面光斑的中心坐标以及定心机构在移动过程中旋转的角度，然后通过坐标修正得到实际中心点坐标。在分析处理数据时，需要对CCD相机进行标定，将图像坐标转换成世界坐标，进而求解出深孔零件轴线的直线度。

2 自定心机构设计

由于检测的深孔零件其内径较小且长径比大，使得在零件内孔中定位和固定常规光电测量元件的难度较大，所以只能将光电测量元件置于零件外部进行测量。因此需要设计一种能够放到深孔零件内部的定心机构，这种机构定心精度高且能真实反映内孔截面中心点信息，同时还需要能够适用于检测内径在一定范围的深孔零件。

本文设计了一种通用性强的基于面接触的自定心机构，其结构框图如图2所示。该定心机构主要由定位螺母1、左弹簧2、左移动楔形件3、可伸缩轴套4、右移动楔形件5、右弹簧6、中心轴8等组成。在没有外力作用时，可伸缩轴套4与两个楔形件3、5的楔形面接触，在两个压缩弹簧2、6的弹力作用下，两个楔形件会往中间靠拢，弹性连接体10在张力作用下扩张，使得可伸缩轴套发生膨胀，最终达到一个独立于外部的动态平衡状态。将定心机构放入零件内孔后，可伸缩轴套4在内孔圆柱面作用下会径向收缩至紧贴内孔壁的状态。当定心机构移动到某一位置后，弹簧、楔形件和可伸缩轴套三者之间会进行动态调整以适应内孔截面的变化，最终达到自动定心的效果。定位螺母1起到一个调节弹簧预紧力的作用。

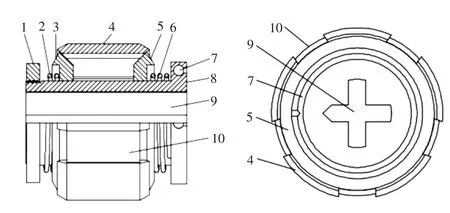
图2 自定心机构结构框图

中心轴7上开有十字形通光孔9，本文之所以采用十字形通光孔，是因为在图像处理时可以根据不同采样位置获取的十字形光斑准确计算出定心机构在移动过程中旋转的角度，再结合测得的中心点偏距就可以对获得的十字形光斑中心点坐标进行修正，可极大地减少装配误差对检测结果的影响，保证检测结果的准确性。

3 十字形光斑中心点坐标提取

3.1 图像处理

采用基于图像骨架的十字中心点坐标提取方法，具体图像处理流程图如图3所示，包括图像采集、图像预处理、形态学处理、中心点提取等。

图3 图像处理流程图

由于电子元器件的电磁干扰、环境光照变化等因素都会给图像带来噪声，噪声会掩盖图像的有效信息，影响图像质量，增大后期图像处理难度。因此首先需要对采集到的图像进行预处理，消除图像中的噪声，使特征信息更加明显，从而提高光斑中心点坐标提取的准确性。

分别采用均值滤波、高斯滤波和中值滤波三钟滤波方式对图像进行降噪处理，不同的滤波结果如图4所示。从滤波结果可以看出，中值滤波不仅能够有效消除毛边和噪声，而且将边缘轮廓信息很好地保留了下来，图像特征变得更加明显。因此采用中值滤波来滤除图像噪声。

图4 不同的滤波结果

为了后续能够计算出光斑的中心点坐标，需要把滤波后的目标光斑区域与图像背景分隔开来。本文选择最大类间方差法来进行图像分割，图像分割后的结果如图5所示。

图5 图像分割结果

3.2 光斑中心点提取

通过图像分割把十字形区域分割出来后，用基于图像形态学的骨架提取方法直接获取十字形区域骨架，此时的骨架是由多个单像素点连接而成的框架结构，如图6（a）所示；然后将骨架框架转化成亚像素级别的XLD轮廓，并通过形态学处理进一步剔除掉无用的骨架分支，处理结果如图6（b）所示；选取图中十字交叉的骨架并计算出交点坐标，该坐标即为十字形区域的中心点坐标。基于图像骨架的中心点提取结果如图6（c）所示。

图6 基于图像骨架的光斑中心点提取

3.3 中心点像素坐标修正

自定心机构在加工和装配过程中可能会产生误差，使得十字形通光孔中心线与被测零件的理论轴心线不重合，导致测得的十字形区域中心点O′与理论中心点O之间存在固定偏距e。理想条件下，自定心机构在深孔零件内部轴向运动时不发生旋转，此时十字形光斑中心点与截面理论中心点同步变化，能够反映实际轴心线的变动量。但是在实际操作过程中，自定心机构会带动十字形通光孔旋转。为了方便计算，以获取的第一个十字形区域中心点与O点的连线为起始线，当定心机构移动一定距离后，十字形光斑中心绕着理论中心点旋转到O″，旋转角度为θ，其旋转模型如图7所示，此时通过图像处理测得的十字形光斑中心坐标为O″点的坐标。

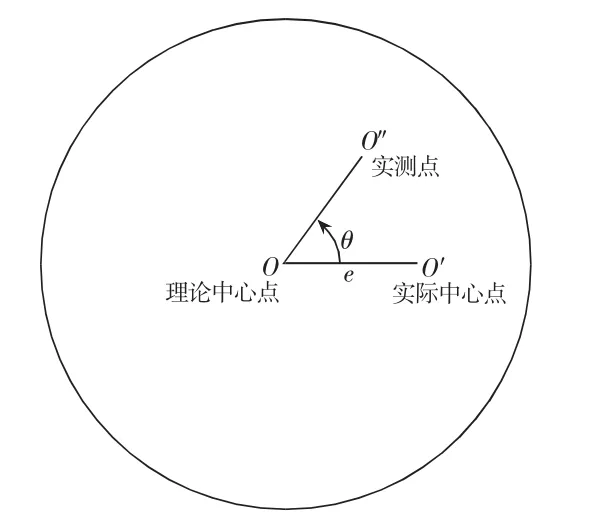
图7 十字形光斑中心点旋转模型

像素坐标系中以向下向右为递增方向，测得O″点像素坐标为（u″，v″），根据转角和固定偏距e可以计算出旋转前O′点的坐标。坐标变换示意图如图8所示，此时O′点相对O″点的变化量Δu＝esinθ，Δv＝e－cosθ。

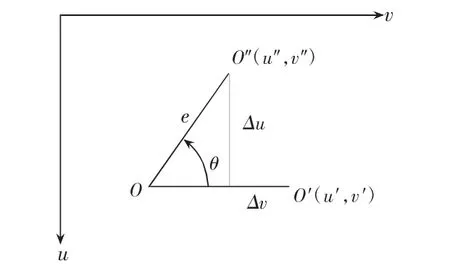
图8 坐标变换示意图

则O′点像素坐标为：

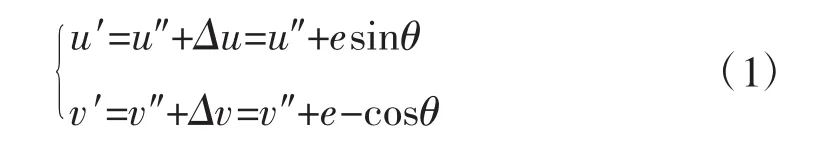
3.4 获取世界坐标系下十字形区域中心点坐标

在计算世界坐标系下各十字形区域的中心点坐标之前，需将中心点的像素坐标转换成图像坐标。建立以物理单位表示的图像坐标系，单位为mm，其x轴和y轴分别与像素坐标中的u轴和v轴平行，以第一个截面理论中心点坐标（u0，v0）为坐标系原点，图像坐标系如图9所示。

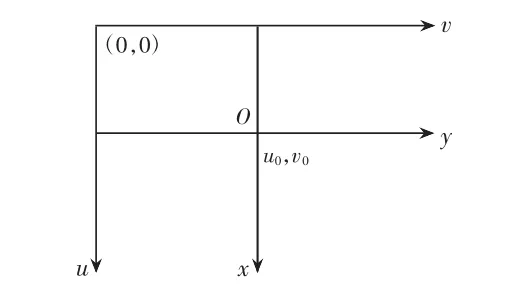
图9 图像坐标系

则像素坐标与图像坐标的转换关系为：

其中，dx，dy分别为单位像素在x轴、y轴方向上的物理距离，可以通过相机标定获得。因此，在图像坐标系下，不同截面十字形区域中心点的坐标可以表示为：

世界坐标系根据图像坐标系建立，其XOY平面与图像平面xoy互相平行，且Oo连线与世界坐标系的Z轴共线，Z轴方向为定心机构的水平运动方向。世界坐标系的原点与深孔零件左端面的中心点重合，则世界坐标系下不同截面十字形区域中心点的坐标O（ixi，yi，z）i可以表示为：

3.5 直线度评定

采用最小二乘法来评定空间轴线直线度误差，其评定模型示意图如图10所示。

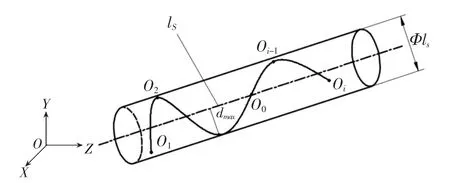
图10 最小二乘法评定空间直线度误差示意图

根据最小二乘原理，首先将实际轴线上的点Oi（xi，yi，zi）进行最小二乘中线拟合，并把得到的最小二乘中线lS代替深孔零件理想的轴心线；然后计算实际轴线上各测点到最小二乘中线的距离di，以距离最大值dmax为半径，最小二乘中线为轴线作理想圆柱面，该圆柱面的直径Φls即为所求的空间轴线直线度误差值f，其中f可表示为：

4 实验与结果

为了验证检测方案的可行性，对一根某型号的短管零件进行测量实验。零件长350mm，内径30mm，外径40mm，直线度要求为0.08mm。取步长L=30mm，采样三组数据，每组测量10个点。实验平台如图11所示。

图11 实验平台

由图像处理得到各截面中心修正坐标后，再通过MATLAB软件拟合最小二乘中线并计算各点到最小二乘中线的距离di，短管零件实验数据如表1所示。从表中可以看出三次测量的最大距离在零件的同一个位置，且三次测量的直线度误差均小于0.08mm，满足检测要求。

表1 短管零件实验数据（mm）

5 结论

针对深孔类零件轴线直线度难以精确测量的问题，本文提出了一种改进的基于光轴原理的直线度检测方法，利用平行激光照射内孔中自定心机构上的十字形通光孔，通过CCD相机将捕获形成的十字形光斑传输至计算机；采用基于图像骨架的十字形光斑中心点坐标提取方法，并根据十字形通光孔旋转角度和坐标变换法对提取的光斑中心点坐标进行修正，减少了系统装配误差的影响；实验结果表明，该方法检测精度较高，且重复性好，具有一定的实际应用价值。