智能配电网线路接地故障电流零差选线方式研究

吉玉琢，韩东，王安斌，姜吉，周航

（1．中国石化集团江苏石油勘探局有限公司，江苏 扬州 225000；2．中国石油化工股份有限公司江苏油田分公司，江苏 扬州 225000）

目前，国内大多数中低压智能配电网络采用小电流接地模式。其中主要包括消弧线圈接地以及中心点不接地两种运行方式，而这种接地模式经常出现单相接地短路故障。一旦出现单相接地故障，会给选线工作造成极大的困难。同时，单相接地故障的发生，令非故障线路的电压速度增大，对于整个智能配电网的稳定性造成冲击。为了有效解决这一问题，相关工作人员需要设计一种更为准确、快速的选线方式，能够在尽可能短的时间内判断出故障线路，并将故障线路与其他线路分离，避免接地故障对电力系统造成进一步的破坏。

1 单相接地故障特征

不接地电网与利用消弧线圈接地的电网，在产生单相接地故障之后，其稳态的基波零序电流在电路中的分布存在差异。为了方便说明，在对小电流系统进行分析的过程中，不考虑电容电流与线路自身的影响（如图1所示）。

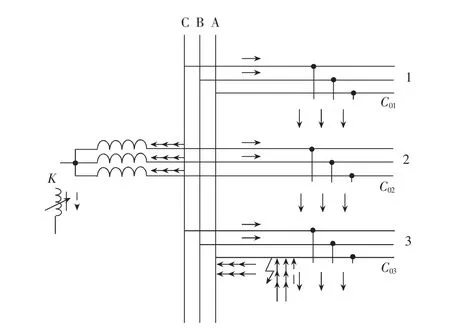
图1 单相接地小电流接地系统电容电流分布示意图

1．1 单相接地故障稳态特征

1．1．1 中性点不接地稳态故障特征

当中性点不接地系统发生单相接地故障之后，其零序电流的等效情况如图2所示。

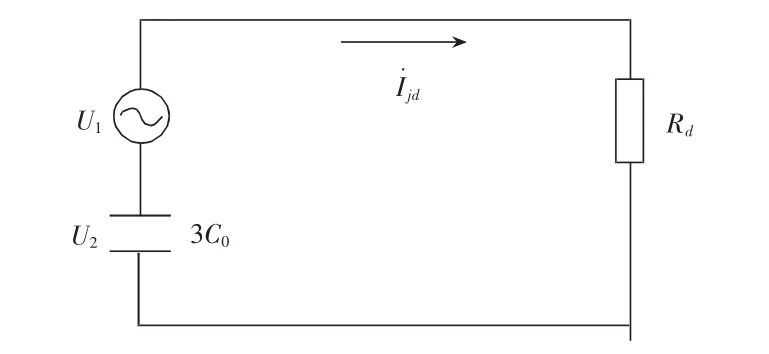
图2 中性点不接地系统单相接地零序电流等效情况示意图

通过对图2的分析可以发现，线路对地电容电流为：

公式（1）（2）（3）中，ICA1、ICB1、ICC1分别代表图1中的A、B、C三项对应的电容电流，而UB与UC则代表当出现单相接地故障之后，BC两项的对地电压。C01代表该系统的对地电容[1]。

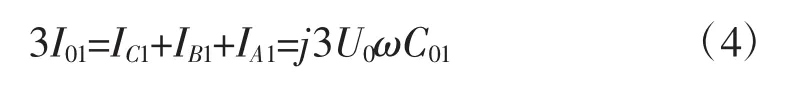
1．1．2 消弧线圈接地稳态故障特征

当电路中接入消弧线圈，其电容电流会在分支线路上产生变化，如果图1中的线路3出现的单相接地故障，则线路3中会产生感应电流（IL），则故障点的电流计算公式为：

公式（5）中，ICE即接地电流，IL则代表线圈产生的感应电流。在相同的方向上，对地电流与感应电流的方向相反，两种电流的相位差为180°，因此当出现单相接地故障，故障点电流数值会变小[2]。

由此可见，接入消弧线圈的电路在实际运行时，由于电容电流的补偿值存在差异，则消弧线圈可能为过补偿，也可能是完全补偿或者欠补偿，故障点零序电流的流向，会根据消弧线圈补偿状态的不同而发生变化。电网在运行过程中，消弧线圈通常会处于过补偿状态，因此零序电流无论是否处于故障状态，其方向不会发生变化，因此无法依靠方向来判断故障线路。

以吸光度为纵坐标(y)，以芦丁质量浓度为横坐标(x)，根据不同浓度芦丁标准品溶液的吸光度，拟合得到线性回归方程为y=12.685x+0.004 99(图1)，R2 =0.999 23，说明相关性较好。

1．2 单相接地故障暂态特征

1．2．1 暂态电感电流

图3中，C代表电路对地电容值，L0为变压器与电路电感的总和，R0为零序电路中的电阻总和，L，rL则为电路有功损耗的电感值与电阻值，U0为零序电压。正常运行时，暂态电容电流的振频较高，消弧线圈的电感高于变压器与电路电感的总和[3]。因此可以忽略有功损耗的电阻值与电感值，只要得到零序电路中的电阻总值以及对地电容值，就可以得出暂态电容电流。

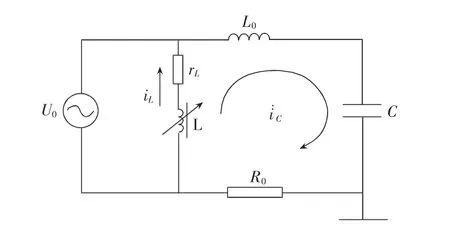
图3 小电流接地系统零序电流等效示意图

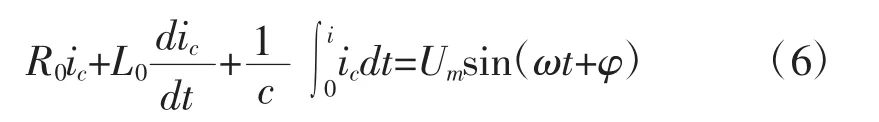
公式（6）中，Um即零序电压的幅值。如果变量，表示线路处于暂态过程中可能会出现震荡或者衰减，如果，表示暂态过程的衰减不具有周期性，将回归稳定。如果智能电网的馈线处于架空状态，则线路的阻抗会保持在250Ω左右，因此可以忽略弧道电阻值。这种状态下，电容电流的自由频率处于300Hz～1500Hz范围内并周期性衰减。

1．2．2 暂态电容电流

当智能配电网出现单相接地故障，消弧线圈会产生感应电流，该电流的计算公式为：

公式（7）中，iL代表感应回路对应的时间，φ则代表线路出现故障之后，相电压的相角。当电路出现故障，电源的角频率与暂态震荡角相同，幅值的大小由发生单相接地故障瞬间的相角所决定，等相角为0时幅值最大，当相角为π/2时幅值最小。

由此可以看出，小电流接地系统一旦出现单相接地故障，则电路中的暂态电流会受到电容电流的影响，电流的频率以及幅值会发生显著变化。如果故障发生之后相电压处于峰值，则电流为最大值，如果故障发生之后相电压为0，则电容电流较小。

2 选线原理

2．1 小波能量算法

平稳信号分析主要以傅里叶理论作为基础，但是出现非平稳信号之后，该理论不再适用。为了解决这一问题，设计人员尝试对傅里叶理论进行变换，目前该理论的变换成果包括循环统计量理论以及小波变换等，本文研究的选线方法就是基于小波变换理论。

2．1．1 连续小波

设计人员设定函数φ（t）的平方可以积分，则φ（t）的傅氏变换φ（ω）满足可容许条件要求：

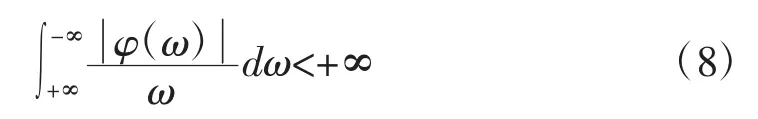
通过对母函数φ（t）进行平移以及收缩，可以得到连续小坡基函数：

2．1．2 离散小波

分析公式（9）可以发现，该函数中存在两个连续变量，即a，b，在计算过程中，a，b多以整数离散的形式存在，因此可以得到φab（t）函数的变换公式：

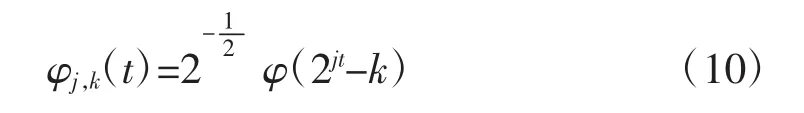
由于变换后的函数φj，k（t）是函数φ（a，b）（t）经过整数倍放大或者平移得到的，且变量j，k∈函数族。因此可以将该形式的小波序列视为离散二进制小波序列。

2．2 选择小波基

想要进行小波变换，前提就是要选定正确的小波基，通过研究发现，小波基的选择与小波变换结果之间存在直接关联。选择小波基时，需要以智能电网实际工作状态作为基础，具体而言就是要以下几项关键的函数特征：①紧支性。小波函数的紧支性，实际上就是该函数不为0的区间，根据离散小波变换特点，应使用具备有限冲激响应功能的小波滤波设备，如果该函数不具备紧支性则需要确保其拥有较短的衰减周期。②正交性。正交性对于选择小波基十分重要，具备正交性就可以确保小波变换过程中，不会出现频率混叠问题。③对称性。如果小波函数具有对称性，即具备线性函数的滤波特性相位，则相位不会出现失真问题。对称性与线性函数相位紧密相关，因此小波基具有对称性特点。④正则性。是对其局部特征进行预估的基础，小波基正则性与其的局部化能力呈现正相关关系，即随着正则性提升小波基在频域中的局部化能力也随之提高[4]。⑤高阶消失矩。小波变换的高频细节中，消失矩与能量呈正比关系，常见的小波函数性质对比表见表1。

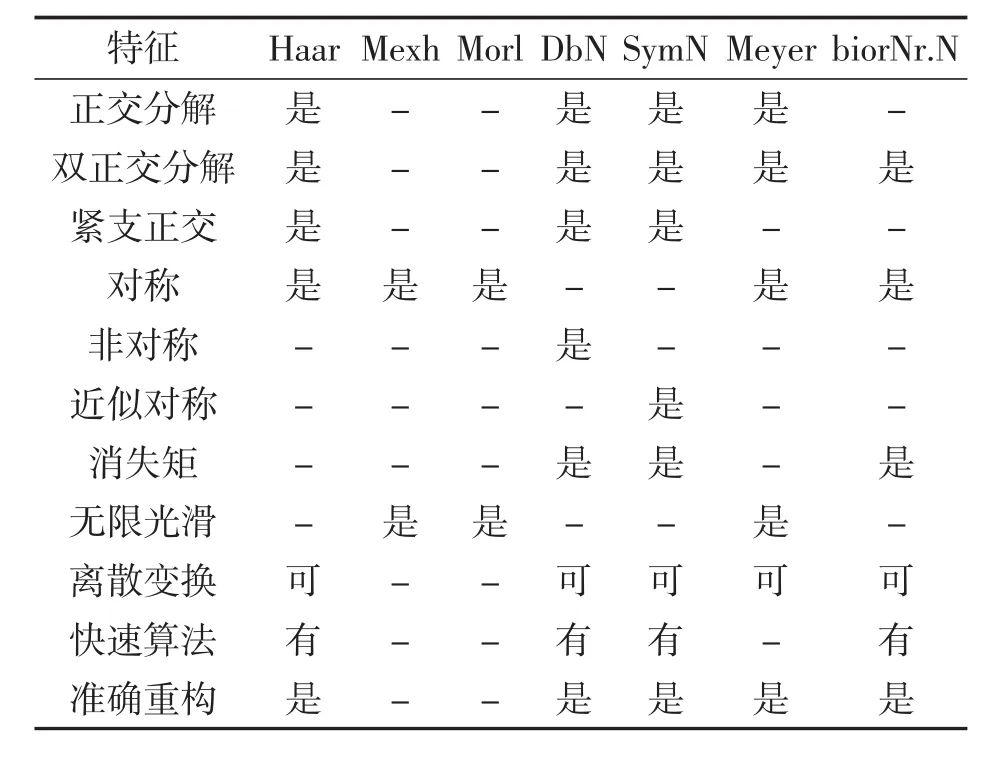
表1 常见小波函数性质对比

同时情况下，研究人员使用Danebchies小波来代表DbN函数，该函数中，Db为函数前缀，而N表示该函数的阶数。通过分析表1可以发现，Db小波函数不具备对称性，但是具备N阶的消失矩以及紧支正交性。一般情况下，该小波函数没有解析表达式，却可以利用表达式表示差分方程的系数。

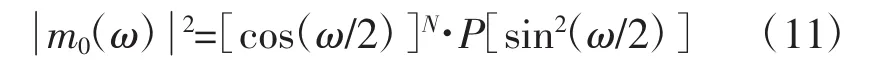
由此可知，Db小波的消失矩参数为（N+1）2，如果变量N增大，函数H（ω）与G（ω）重叠概率将会降低。小波的分频与函数DbN中的变量N联系紧密，因此本次设计中，工作人员使用Db6对暂态信号进行检测与分析。

3 选线流程

第一，在智能配电网变电站中安装远程监测设备，读取电压以及零序电流数据，并依照数据读取的顺序对馈线进行编号。例如将电压数据编为U0，每一条馈线的电流编为I0L1，I0L2，I0L3……I0Ln。编好序号之后，工作人员开始选定选线的启动信号，本次设计中将电压U0作为启动信号，并对该线路的电压进行实时监测，同时给定一个电压值Uset，Uset的数值是相电压的一半，如果监测到该线路中U0数值高于Uset，则可以判定该线路出现的故障，立刻开始进行零序电流求差[5]。

公式（12）中，△I0Li代表线路i与线路j的零序电流差，一共有个，这其中n代表线路中馈线回路的数量。

第二，馈线线路i与j的暂态零序电流，在第二分解层内的能量表达公式为：

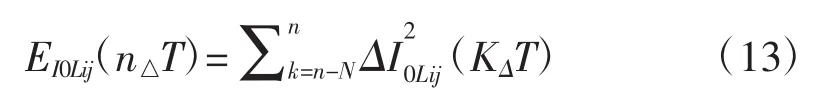
公式（13）中，变量N代表不同时间窗口数据采样的数量，n为数据采样总量，T则代表相邻两条馈线采集点的时间差。

第三，对每一条线路的零序电流差进行求和，公式为：

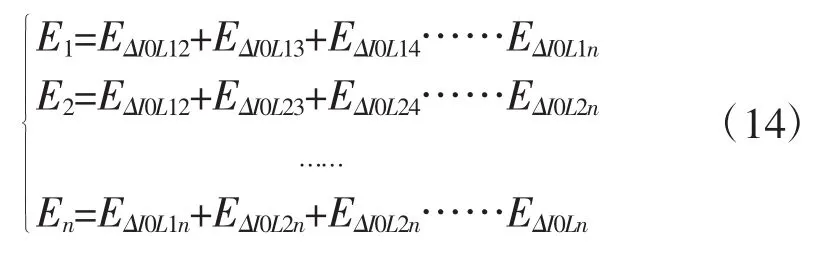
公式（14）中，变量En代表第n条馈线差的暂态零序电流能量和。

第四，对第四层、第五层的零序电流能量进行求和，并对计算结果进行对比，选择其中能量最大时对应的层数，该层即为最佳分阶层，并依据公式（15）计算每一条馈线的能量占比。

第五，判断故障线路，存在单相接地故障的线路会出现大量噪声，并且该线路的三相会产生不平衡电流，导致保护电流显著提高，因此会对选线产生影响。针对这一问题，需要通过确定阈值的方式提升选线的准确性。如果每一条馈线的η值均不高于设定阈值，则代表故障点在母线上，如果某一条馈线的η值高于阈值，则代表该线路存在故障。

4 结论

由于智能配电网系统较为繁杂，馈线数量多，一旦出现单相接地故障，如何快速确定故障线路就成为了一个难题。传统的选线方式存在一定局限性，无法满足目前智能配电网的用电需求。因此，工作人员综合考虑单相接地故障特征，基于小波能量算法设计电流零差选线方式，有效提升选线效率，为确保智能配电网的稳定运行提供技术支持。