加权动态GM(1,1)模型在高速铁路沉降预测中的应用
潘 慧
(浙江省国土勘测规划有限公司杭州分公司 浙江杭州 310030)
近年来,我国高速铁路发展迅速,其运行安全成为人们关注的重点。对高速铁路进行沉降监测并对其数据做进一步分析与预测,对于安全运行具有重要意义。然而高速铁路沉降监测数据的采集受多种因素的影响,如何利用已有沉降监测数据来预测高速铁路沉降并提高预测精度是目前的研究对象。目前常用的时间序列预测模型包括人工神经网络模型、卡尔曼滤波模型及灰色系统模型等,其中灰色系统模型中最常用是传统GM(1,1)模型。传统GM(1,1)模型的优点是“小样本、贫信息”,但受环境干扰较大,且当原始数据序列出现较大波动时,该模型预测会产生较大误差,导致预测精度不高。原始数据序列加权是提高模型精度的众多方法之一,目前已有学者做了相关研究。赵泽昆等[1]利用权递增因子构建权矩阵,建立了非等间距加权 GM(1,1) 模型 ,并证明了时间加权-新陈代谢GM(1,1)模型比传统的GM(1,1)模型的预测精度高;赵建飞等[2]将权作为原始序列的平滑因子,借助Matlab自编程序反复试验得出权值,并验证了加权GM(1,1)模型在地铁沉降变形分析中的有效性、实用性和正确性。以上研究中权值大小随时间递增,充分考虑了新信息优先原理,在一定程度上提高了模型的精度,但却忽略了误差对原始数据可信度的影响,存在一定的局限性。
本文运用相对误差与时间距离相结合的定权方法,引入新陈代谢思想,建立一种新的加权动态GM(1,1)模型,并将传统GM(1,1)模型、加权GM(1,1)模型和加权动态GM(1,1)模型应用到高速铁路沉降预测中,通过实验验证加权动态GM(1,1)模型在高速铁路沉降预测中的优越性。
1 传统GM(1,1)模型构建
灰色理论可以从杂乱无章的原始时间线序列中找出内在规律,解决小样本中信息不完备的随机时间序列问题,为解决信息量少、规律性不强的数据提供了重要的处理方法。
假设原始序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)} ,对X(0)做一次累加,得到以下序列[3]:
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
(1)

k=1,2,…,n。
(2)
2 加权动态GM(1,1)模型构建
2.1 原始序列加权
时间序列中不同时间点对应的值都应加上一个表征其可靠性的权值[4],但是在传统GM(1,1)中,所有时间点对应的值都被视为同等重要,因此使用GM(1,1)模型对序列建模,都会降低拟合与预测的精度[5]。为了提高模型精度,本文在传统GM(1,1)模型的基础上,结合时间距离与传统GM(1,1)模型一次拟合相对误差对时间序列加权,其中,相对误差反映了模型受外界环境的影响,用来剔除时间序列中的影响因子;加入时间距离,用来突出新旧时间序列值重要性的差异,提高距离预测点较近时间点对应数据的利用率。
假设一序列ε=[ε(1),ε(2),…,ε(n)]为传统GM(1,1)模型对原始时间序列拟合后得到的残差值,此序列的相对误差可表示为
(3)
距时间序列初始值的时间距离dt=k-1(t=1,2,…,n),设初始值x(1)(1)=x(0)(1),ρ(1)=1,可以得到
(4)
在传统模型式中加入式(4),得到最终的还原式为
(5)
式中:ρ为权值;a为发展系数,反映时间序列的发展趋势;b为灰作用量,反映数据间的变化关系。
2.2 加权动态GM(1,1)模型
与老信息相比,新信息在认知上会有更大的作用,故加权动态GM(1,1)模型的建立有利于体现新信息的优势。在维度保持一致的情况下,通过加权模型可以求出在n+1时刻的预测值,即使用x(0)(n+1)替换原始序列中的x(0)(1),原始序列可变换为(x(0)(2),x(0)(3),…,x(0)(n+1)),通过模型进一步求出n+2时刻的预测值,直至求出所有预测值。
2.3 精度验证
对加权动态GM(1,1)模型的稳定性与可靠性进行验证,需检验其拟合与预测精度。常用的精度检验方法有小误差概率合格模型、均方差比合格模型和残差检验合格模型[5]。
2.3.1 小误差概率合格模型
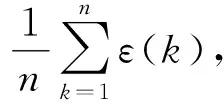
2.3.2 均方差比合格模型
2.3.3 残差检验合格模型


表1 精度检验等级Tab.1 Levels of Accuracy Inspection精度等级小误差概率均方差比值平均相对误差一级0.950.350.01二级0.800.500.05三级0.700.600.10四级0.600.800.20
3 实例分析
构建传统模型、加权模型和加权动态模型,然后对比分析3种模型的拟合值和预测值。试验数据为某高速铁路中DK1137+711断面的累计沉降序列,选取第10~27期累积沉降数据进行建模,第28~30期累积沉降数据用于对传统GM(1,1)模型、加权GM(1,1)模型和加权动态GM(1,1)模型的预测效果进行检验。
3种模型拟合值的平均残差分别为 0.268 mm、0.214 mm和0.137 mm,平均相对拟合误差分别为13.372%、9.283%和6.524%。传统GM(1,1)模型的最大拟合残差为0.607 mm,最小拟合残差为0.027 mm;加权GM(1,1)模型的最大拟合残差为0.447 mm,最小拟合残差为0.057 mm;加权动态GM(1,1)模型的最大拟合残差为 0.374 mm,最小拟合残差为0.028 mm。表2为利用传统GM(1,1)模型、加权GM(1,1)模型和加权动态GM(1,1)模型得到的3期预测值。
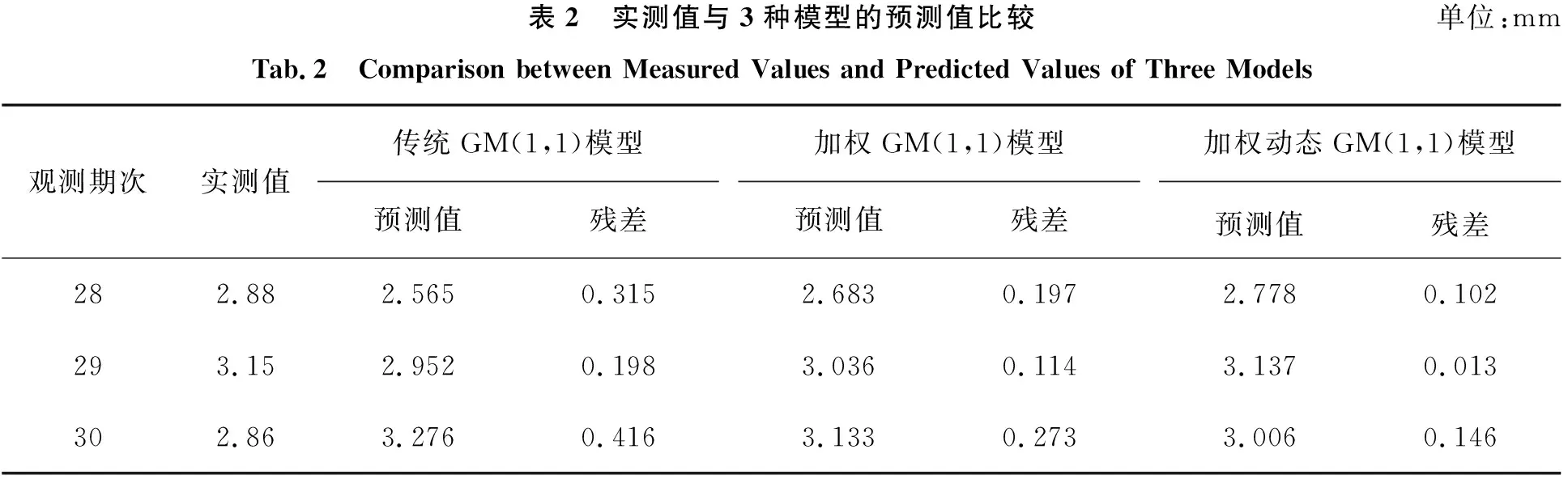
表2 实测值与3种模型的预测值比较单位:mmTab.2 Comparison between Measured Values and Predicted Values of Three Models观测期次实测值传统GM(1,1)模型预测值残差加权GM(1,1)模型预测值残差加权动态GM(1,1)模型预测值残差282.882.5650.3152.6830.1972.7780.102293.152.9520.1983.0360.1143.1370.013302.863.2760.4163.1330.2733.0060.146
由表2可知,对高速铁路沉降数据建模后预测得到的3期数据的平均残差分别为0.310 mm、0.195 mm和0.087 mm,平均相对预测误差分别为10.590%、6.668%和3.020%。通过残差检验合格模型对3种模型拟合预测的结果进行检验,结果如表3所示。
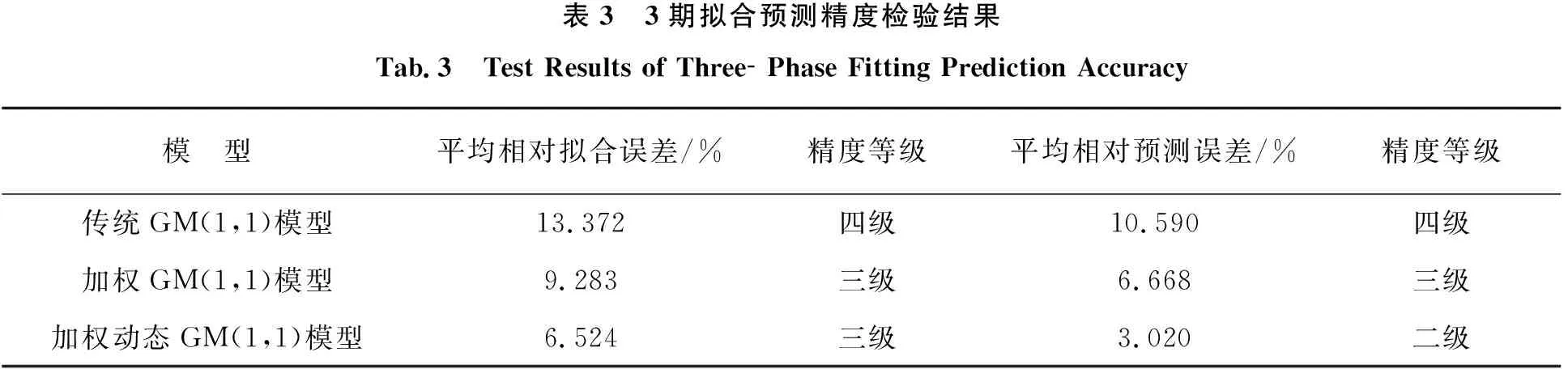
表3 3期拟合预测精度检验结果Tab.3 Test Results of Three Phase Fitting Prediction Accuracy模 型平均相对拟合误差/%精度等级平均相对预测误差/%精度等级传统GM(1,1)模型13.372四级10.590四级加权GM(1,1)模型9.283三级6.668三级加权动态GM(1,1)模型6.524三级3.020二级
从表3可知,与传统GM(1,1)模型相比,加权动态GM(1,1)模型的平均相对拟合误差与平均相对预测误差都有了较大程度的降低,精度提高较为明显,尤其是预测精度,由四级提升到二级。为了更直观地反映3种模型对高速铁路数据的拟合与预测结果,绘制拟合预测值与拟合预测残差值折线图(图1)。
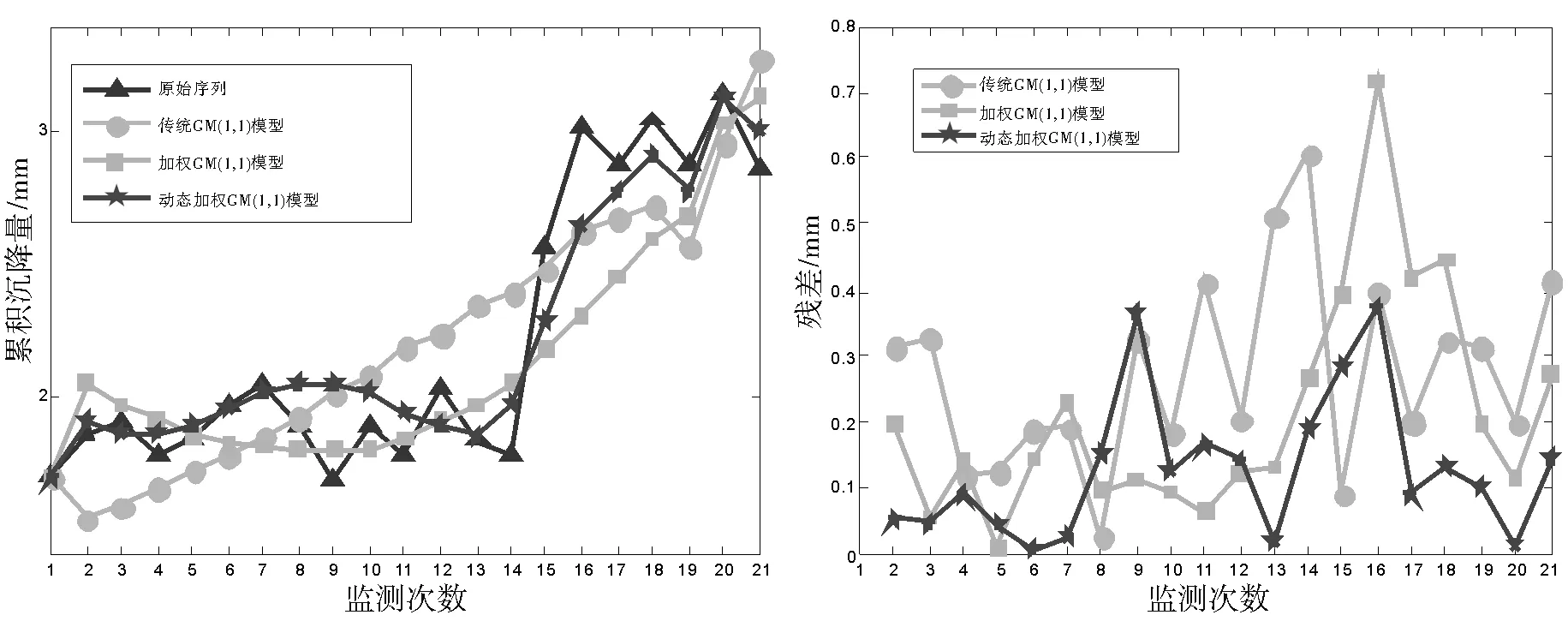
图1 断面监测点3期拟合预测值与拟合预测残差值Fig.1 Fitting Prediction Values and Fitting Prediction Residual Values of Section Monitoring Points in Three- Phase
由图1可知,加权动态GM(1,1)模型拟合预测结果与实测值最相近,拟合预测结果的残差值波动最小,并且在原始时间序列波动较大的情况下依然能够保持较好的拟合预测精度。采用同样的方法对4期和5期数据进行预测,得到的检验精度统计结果如表4所示。

表4 4期和5期拟合预测精度检验结果Tab.4 Test Results of Fitting Prediction Accuracy in Four Phase and Five Phase期 数模 型平均相对拟合误差/%精度等级平均相对预测误差/%精度等级4期传统GM(1,1)模型13.372四级14.836四级加权GM(1,1)模型9.283三级8.196三级加权动态GM(1,1)模型6.524三级4.085二级5期传统GM(1,1)模型13.372四级16.574四级加权GM(1,1)模型9.283三级9.884三级加权动态GM(1,1)模型6.524三级5.165三级
从表4可以看到,随着预测期数的增加,3种模型的预测精度都有所降低,但加权动态GM(1,1)模型精度降低的速率比另外两种模型的小;加权动态GM(1,1)模型预测5期数据的平均相对误差为5.165%,可以达到三级精度等级。
4 结 语
本文采用某高速铁路中DK1137+711断面的累计沉降序列数据,利用传统GM(1,1)模型、加权GM(1,1)模型和加权动态GM(1,1)模型进行沉降预测试验,并对3种模型的试验结果进行对比分析和验证。结果表明,3种模型都能对高速铁路进行准确的沉降监测与预测,其中,加权动态GM(1,1)模型可将相对误差视为误差影响因子予以剔除,提高了新信息的利用率,并且可以减少数据中的随机误差,比其他两种预测模型的拟合精度与预测精度更高。加权动态GM(1,1)模型用于高速铁路沉降监测具有高效性与准确性,可以反映出高速铁路沉降变形规律,对于高速铁路沉降监测与预测具有一定参考价值。

