基于重心法和禁忌搜索算法的配送中心选址

褚东亮 李帆

[摘要]在考虑运输费用和运输碳排放成本的因素下，研究了配送中心的选址问题。针对重心法在配送中心选址中存在的局限性，在重心法的基础上，通过禁忌搜索算法（Tabu Search Algorithm，TSA），进一步优化选址，从而选出适合建立配送中心的城市。以Z公司为例，综合运用重心法和TSA进行选址，以运输成本为目标同时与位置度量法、重心法与层次分析法相结合的选址结果分别进行对比，证明了重心法与TSA在配送中心选址中的实用可行性和优越性。

[关键词]配送中心;选址;重心法;禁忌搜索算法

[中图分类号]F252.14     [文献标识码]A[文章编号]1005-152X（2022）03-0063-06

Site Selection of Distribution Centers Based on Centroid Method and Tabu Search Algorithm

CHU Dongliang， LI Fan

（Beijing Key Laboratory of Logistics System &Technology（School of Logistics， Beijing Wuzi University）Beijing Tongzhou 101149， China）

Abstract： Considering the transportation and carbon emission cost， the paper studied the site selection of distribution centers. In view of the limitations of the centroid method in this problem， the paper combined the centroid method and the tabu search algorithm so as to pick out suitable cities to host the distribution centers. Taking the company Z as an example， it used centroid method and tabu search algorithm comprehensively for site selection. With the goal of transportation cost optimization， it compared the result from the location metric method and from the method of this paper， which proved the feasibility and superiority of the centroid method and TSA in distribution center site selection.

Keywords： distribution center; site selection; centroid method; tabu search algorithm

0 引言

配送中心被稱为物流系统的中枢或枢纽，是物流系统中的重要设施。而配送中心建设成本高，并且建成之后难以进行迁移，所以合理的配送中心选址能够做到在尽量控制成本的情况下，提升物流服务水平，使企业在同类中脱颖而出。因此配送中心选址的合理性与实现企业物流降本增效有密切联系，配送中心的选址能够影响企业未来的发展。

国外在选址问题方面的研究开始得比较早。 Alfred，等[1]是最早提出选址理论的，其思索的选址问题是选定一个仓库的方位，使仓库到几个分散的需求点的距离最短。Bettinger，等[2]较早采用TSA，从多个方案中选取最佳的方案来计划木材的采伐。在此基础上国内外学者都对选址问题进行了进一步研究，在研究方法上不断创新和改进。杨娜娜，等[3]将 SIC模型应用于东莞市公交冗余站点优化中，采用 TSA进行最优求解。杨珺，等[4]提出了电动汽车换电站选址与配送路径优化问题，建立了使用TSA-改进 Clarke-Wright 节省的两阶段启发式算法来求解模型。陈诗军，等[5]对TSA 的代价函数、邻域产生规则以及解禁规则进行了改进，通过这种改进算法对基站布局进行了优化。Mauricio，等[6]采用基于TSA 的方法来解决容量p值中位数问题，对肉制品公司的配送中心进行了选址。Alavi S，等[7]为降低配送中心到制造商的运输成本建立了模型，运用TSA求解该模型。Zhen Lu，等[8]针对大规模问题使用TSA，验证了其所提出的确定配送中心位置的模型的有效性。

由此可以看出，TSA在选址优化方面的运用是有迹可循的，通过与其它算法相结合，互相弥补，能够有效解决一些问题。而重心法通过与其它算法联合使用，同样能够解决最优选址决策问题，提高选址的精确性与合理性。

运输成本和碳排放一直是学者在各类优化问题中考虑的重要因素。李明，等[9]在多物流配送中心选址布局问题的研究中，其目标函数设定为直接与间接运输成本之和。戴卓[10]关于三层物流网络研究问题中，运输成本是总成本的重要构成因素。孟燕萍，等[11]在动态应急物资选址问题中，建立了以最小化应急物资运输成本和灾民等待物资心理惩罚成本为目标的多目标混合整数规划模型。戢守峰，等[12]考虑存在拥堵和限速的路况依赖下，构建了以经济总成本最小和碳排放量最小为目标的多目标模型。王梦梦，等[13]以最小化成本和碳排放为目标，建立了供应链优化模型。蒋海青，等[14]在开放选址-路径问题中考虑了碳排放的因素。

由于重心法本身的局限性，选出的位置可能并不是建立配送中心最优的位置，就需要进一步的计算。首先采用重心法进行选址，对得到的地理位置进行分析探讨，在该地建立配送中心是否具有可行性，若是，则建立配送中心;若否，则通过观察地图得到被选中城镇附近的城镇，通过TSA在这些附近的城镇中选出最适合建立配送中心的城镇，作为配送中心建立的地址，计算思路流程如图1所示。

1 配送中心选址模型构建

本文以城市的配送中心为研究对象，对配送中心的选址问题进行研究。设有n个需求点，xi为需求点的横坐标，yi为需求点的纵坐标，需求点的坐标为各个需求点的经纬度 M（xi，yi）（i=1，2， …，n），例如北京（116，39），拟建立的配送中心的坐标为（x，y）。

1.1 模型假设

重心法和禁忌搜索算法的配送中心选址模型构建基于以下假设条件：

（1）配送中心到需求点之间的道路问题忽略不计;

（2）暂时不考虑工程建设项目的总投资，比如建立配送中心地址的土地价格等;

（3）假设运输费用是线性函数，随着距离的增加而增加相同的比例;

（4）需求点的需求量都是已知条件，并且需求点与需求数量不变;

（5）假设经线纬线是坐标系，各个地点的经纬度为各个需求点的坐标，并且需求都来自于这一个点;

（6）不考虑运输车辆遇到不可抗力时增加的碳排放成本;

（7）假设运输过程中车辆运载量与所需消耗的燃油量呈线性函数。

1.2 符号说明

本文中涉及的符号及其含义如下：

ci表示货物从（x，y）运送到需求点M（xi，yi）所在地所需费用;

hi表示运输费率，即每运送1km 的1t貨物所需费用;

di表示从配送中心到需求城市的距离;

wi表示货物的运输量;

λ表示车辆的平均耗油量;

m表示车辆负载;

α表示燃油的二氧化碳排放系数;

H1表示货物的运输费用;

H2表示货物运输的碳排放成本;

K为常数参数，较正从坐标到距离计算过程中的误差;

Q表示备选配送中心的位置。

1.3 模型构建

本文主要考虑了配送过程中的运输费用及运输过程中的碳排放成本。

运输费用：

因此，两个目标分别为运输费用 H1和碳排放成本H2，即总目标函数为运输成本H。

1.4 算法设计

1.4.1 重心法。重心法只考虑配送中心与需求点之间的距离 d1i ，故通过式（5）作为距离计算公式对运输费用进行计算。

求解运费的最小值，即对函数 H1（x，y）求极值问题，分别对x，y求偏导数，令偏导数为零，解得：

由于算式中含有di1，而 di1含有未知数，所以首先假设开始时的 x 和 y 是生产基地的位置，再进行迭代，直到求出最小的运输成本，以及最小成本所对应的坐标。

1.4.2 TSA模型。初始解：由于TSA对初始解的要求比较高，所以初始解设定为由重心法计算出来的选址地点。

代价函数：由于得到的是地理坐标，也就是经纬度，所以要通过计算求出实际配送距离。假设A，B 两点之间的地理坐标分别为A（X1，Y1）、B（X2，Y2），经过 AB两点的大圆的劣弧长度即为两点的实际距离。以地心作为原点坐标，赤道平面为XOY平面，以0度经线圈所在的平面建立空间直角坐标系，则AB两点的球坐标分别为 A（RcosX1 cos Y1，R sin Y1 cos Y1， R sin Y1）， BR cosX2 cos Y2，R sinX2 cos Y2，R sin Y2，其中 R 为地球半径6 370km，则AB两点之间的实际距离为：

化简得到：

由前文的优化目标可知，选址过程中的运输费用和运输碳排放成本即为由式（9）带入式（3）得到的代价函数，见式（10）。

邻域：邻域是指初始解附近有建立配送中心条件的地区的坐标。邻域产生规则是对这些坐标进行迭代，例如把配送中心拟选定的位置标号为ABCD，对于路径1A23，将 A 替换成 B，就得到新的路径1B23。

禁忌表：禁忌最先出现的距离值。禁忌表记录了最近搜索过程中已经出现的解，这些解禁止在近期内重复出现，从而避免陷入局部最优解。达到一定的迭代次数之后，禁忌表会依次释放这些禁忌对象，对象被释放之后，重新参与到计算中。设置适当的禁忌长度，在该解添加到禁忌表中时，对禁忌长度进行初始化。与此同时，写入加入禁忌表时解的代价值。算法每次对禁忌表进行写入时，更新禁忌表，对上一步禁忌的元素的长度减1。直到禁忌长度为0时，解禁。

解禁规则：当有解优于现今为止最好的解并且已经被禁忌时，解禁这个解，并且将这个解当作是现今为止最好的解。如果没有优于现今为止最优的解，即所有的解都解禁也没有比当前最优解更好的解了，那么，把禁忌表中代价值有所降低的解解禁。如果没有代价已经降低的可选的解存在，那么在禁忌表中选择代价最低的进行解禁。

终止规则：当到达最大迭代次数时，程序终止。根据以上的参数设计进行计算迭代即可。

2 实例验证及结果分析

2.1 问题分析

Z公司承接的重点客户在杭州、重庆、长春有三个生产基地，由于业务拓展到全国各地，公司决定建立配送中心服务客户和自身发展。按照传统的地区划分，把全国划分为华中、华北、华东、华南、西南以及西北地区和东北地区。在不同的区域建设各自的配送中心，这个配送中心就承担该区域内的物资配送的任务。

由于客户公司在杭州、重庆和长春有生产基地，杭州的月生产量为4万t，重庆的月生产量为4万t，长春的月生产量为2万t，并且其生产基地本身具备配送中心的功能，故为了节省成本，在东北地区、华北地区和西南地区暂不打算建立单独的配送中心，并且由于长春现在运往华北地区的线路比较成熟，交通比较便利，暂不打算在华北地区建立配送中心，只需在西北和华南地区建立配送中心。由于重庆距离西北地区较近，为方便产品运输，由重庆的生产基地运往西北各个城市。虽然杭州生产基地距离华南地区较近，但是根据需求量数据统计得出杭州生产基地的生产量不足以支持华东地区和华北地区两个地区的需求，所以华南地区从另一稍近生产地重庆运往各个需求点。

2.2 计算

首先通过重心法进行选址计算。由于是从重庆的生产基地运往新建的配送中心，故初始坐标假设为重庆生产基地的坐标，再进行迭代。通过对表1数据进行整理和分析，运费率约为0.20CNY/t/km（运费数据来自铁路货物运费查询官网）。

通过表1计算出的运费H1，令K=111，对经纬度坐标进行计算，把坐标距离转化为估算的实际距离d1i，由需求量可得到运输量为wi，把这些参数带入到式（1），就能够得到运输费用;λ为1.25kg/t ·km，α为燃油二氧化碳排放系数[14]，为2.63kg ·L-1，碳税价格依据澳大利亚政府碳税法案中相关标准，每吨碳排放征收23澳元，折合成人民币约每千克 CO2征收0.11425元[15-17]。以此计算碳排放成本H2。把迭代的初始坐标设置为重庆市的坐标，再用线性规划进行求解，就能够得到重心法求解出的两个配送中心的备选地址，其地理坐标分别 Q1（103，35.9998）和 Q2（112.9999，22.99991）。

通过百度地图的坐标拾取系统得到关于该位置的相关信息。对于位置 Q2来说，选中的位置虽然在佛山丹灶特大桥，但是该点附近不仅建有多个物流中心，而且还有佛山南庄码头，交通便利，可以多样化货物的运输方式，所以在Q2附近进行选址，有独特的优势。地理坐标为Q1的地点位于临夏自治州的马塔山附近，交通不便，故需要对该选址做调整。通过地图可以看出 Q1附近临近公路和铁路的城镇，选出数个城镇，通过TSA进行迭代，得到最优的组合是重庆→乌鲁木齐→西安→银川→小茨沟站，于是得出结论，配送中心的最优选址位置在小茨沟站，与此同时，小茨沟站是火车的停靠站点，有利于货物运输。

2.3 结果分析

选择既考虑定性因素，又考虑定量因素的选址方法，采用位置度量法进行计算，考虑到该配送中心选址的实际情况，为该公司选址时主要考虑的客观因素有工资平均水平、工业用地成交均价（CNY/m2）以及运输成本（CNY/km），主观因素主要考虑竞争状况、地理位置和环境3个因素。综合客观因素和主观因素的度量值和重要性的总评比值，总评比值较大的为最优方案，通过位置度量值的计算，可以得到配送中心的选址地址位于兰州和武汉。

同时利用重心法选址能够找到一个范围，范围中会包含几个备选点，之后利用层次分析法辅助重心法完成最终的选址。在每个区域中通过重心法计算得到一个中心位置，以该中心为原点，合理长度为半径，以求在该圆内至少包含3个或更多的城市，之后通过层次分析法得到层次总排序表，确定最终的物流配送中心位置。计算得到配送中心的选址地址位于西安和广州。

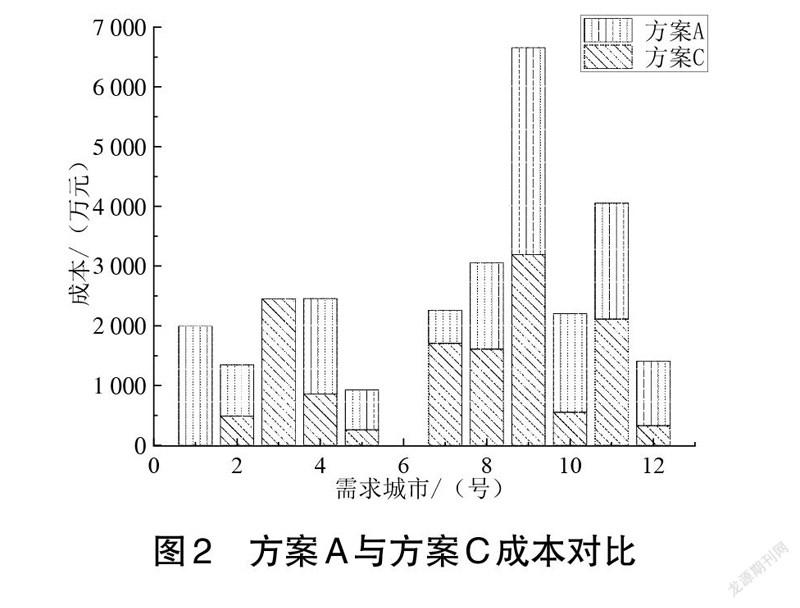
把本文通过重心法与TSA计算出的结果记作方案A，通过位置度量法计算的结果记作方案 B，而采用重心法和层次分析法计算的结果记作方案 C。通过式（9）分别计算运输距离，通过给出和计算出的需求量与单位运费率计算，得到表2。图2为方案A 与方案C 的成本对比情况，可以看出方案C 的费用所占面积略大于方案A，因此可以得出方案A总成本低于方案 C 的结论;与此同时，从数据上可以计算出，方案 C 高于方案A 成本3 259万元。方案 A 与方案 B 的成本对比如图3 所示，可以明显看出方案B 的面积大于方案A，即方案A优于方案B。通过计算同样发现，采用重心法和TSA计算出的选址地址，其总运费大约为13566万元。对于方案 B，其总运费费用为 16825万元，对于运费来说，节省了19.37%的费用，使得企业的成本有了大幅度的下降。对于方案 C，其总运费费用为15249万元，对于运费来说，节省了 11.04%的费用。总的来说，就运输成本来看，方案 A优于方案B和方案C。

3 结语

在考虑运输距离、单位运输费用、运量以及碳排放的条件下，本文采用重心法这一经典的配送中心选址方法，计算出备选的配送中心地址是在佛山丹灶特大桥与佛山南庄码头以及临夏自治州的马塔山附近。但是在考虑运输条件的情况下，通过TSA选址结果由马塔山优化为了小茨沟站，可以得出以下结论：

（1）以运输成本最小化为目标，结合重心法和 TSA，对Z公司的配送中心进行了选址计算。重心法使用简单方便，TSA是人工智能在组合优化算法中的一个成功应用，但是单独使用都具有局限性，通过Z 公司这一实例，互相补充了算法中的部分不足之处。

（2）通过与位置度量法、重心法与层次分析法相结合所计算出的结果进行对比，得出重心法与TSA 相结合，企业的运输成本花费更小，总成本更低这一结论。

（3）计算得出的选址地址具备一定的实施价值。对于Z公司的配送中心选址问题的解决有所帮助，使Z公司能够更加客观地对物流配送中心选址进行规划，从而选出更科学、更经济的配送中心。但是由于并未考虑地价等成本，所以其配送中心选址是有局限性的。

[参考文献]

[1] ALFRED W，FRIEDRICH C J.Alfred weber’s theory of the location of industries[M].Chicago，Ill The University of Chi- cago Press，1929.

[2] BETTINGER P，SESSIONS J，BOSTON K.Using Tabu searchto schedule timber harves TSA subject to spatial wildlife goals for big game[J].Ecological Modelling，1997，94（2）：111-123.

[3] 楊娜娜，张青年，黄健锋.禁忌搜索与SIC模型结合在公交冗余站点优化中的应用[J].中山大学学报（自然科学版）， 2015，54（4）：150-157.

[4] 杨珺，冯鹏祥，孙昊，等.电动汽车物流配送系统的换电站选址与路径优化问题研究[J].中国管理学，2015，23（9）：87-96.

[5] 陈诗军，王慧强，陈大伟，等.基于改进禁忌搜索的基站布局优化算法[J].计算机工程与科学，2018，40（2）：341-347.

[6] MAURICIO R M，VELAZQUEZ R G，MARTIN E A，etal.Solution search for the capacitated p-median problem us- ing Tabu search[J].International Journal of Combinatorial Optimization Problems& Informatics，2019，10（2）：17-25.

[7] ALAVI S，AZAD N，HEYDAR M，etal.Integrated production，inventory， and location allocation decisions in designing sup- ply chain networks[J].International Journal of Information Systems and Supply Chain Management，2016，9（4）：22-42.

[8] ZHEN Lu，WUYiwei，WANGShuaian，etal.Capacitated closed-loop supply chain network design under uncertainty[J].Ad- vanced Engineering Informatics，2018，38：306-315.

[9] 李明，刘航，张晓建.多物流配送中心的选址布局问题优化模型研究[J].重庆交通大学学报（自然科学版），2017，36（1）：97-102.

[10]戴卓.三层物流网络选址：路径优化及混合启发式算法研究[J].计算机应用研究，2017，34（8）：2349-2354.

[11]孟燕萍，申慢慢.考虑灾后道路恢复情况下动态应急物资选址问题[J].重庆交通大学学报（自然科学版），2019，38（1）：89-96.

[12]戢守峰，唐金环，蓝海燕，等.考虑选址-路径-库存联合优化的碳排放多目标模型与算法[J].管理工程学报，2016，30（3）：224-231.

[13]王梦梦，韩晓龙.考虑碳排放的易腐品供应链选址-路径-库存联合优化[J].上海海事大学学报，2019，40（4）：45-51.

[14]蒋海青，赵燕伟，张景玲，等.基于碳排放的开放选址-路径问题及算法[J].系统工程理论与实践，2020，40（1）：182-194.

[15]莫司丞.粤海火车渡轮燃油消耗原因分析与对策研究[D].成都：西南交通大学，2013.

[16]刘炎宝，王珂，杨智勇，等.考虑碳排放与新鲜度的冷链物流配送路径优化[J].江西师范大學学报（自然科学版）， 2019，43（2）：188-195.

[17]林殿盛，张智勇，王佳欣，等.需求不确定下的低碳物流配送中心选址[J].控制与决策，2020，35（2）：492-500.