基于“三个理解”的初中数学探究能力培养策略

摘要：文章从树立学生探究意识，关注合作探究，发展学生探究能力;变式延伸，发展学生思维能力等方面深入分析并讨论初中数学教学中培养学生的探究能力的策略.

关键词：“三个理解”;初中数学;探究能力;培养对策

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）11-0032-03

收稿日期：2022-01-15

作者简介：黄秋芳（1981.8-），女，江苏省苏州人，本科，中学高级教师，从事中学数学教学研究.

初中数学是一门逻辑性与思维性兼备的学科，在课程教学中增强学生对知识技能的探究能力，发展学生解决问题思维能力，是教育教学活动的主要目标.初中数学教师应该在教学过程中革新教学理念，立足于初中学生学习成长的特点，给学生设计高效的学习方案.而发散性思维便于延伸学生学习思路，培养学生灵动的思维方式，学生在不断地探究与分析中掌握举一反三的技能，实现学生多个维度学习与运用知识点.结合张建跃提出的“三个理解”教学理念，谈谈如何在初中数学教学中培养学生探究能力.

1 初中数学教学中培养学生探究能力的前提条件针对“三个理解”，也就是理解数学、理解学生和理解教学，在培养学生探究能力过程中，教师立足于“三个理解”的思想理念，针对性地设计教学环节与教学内容，将“三个理解”的教学理念融入初中数学课堂教学中，全面提升数学教学质量.

1.1 理解数学

在课堂教学中，理解数学是数学学科教学活动的基础，教师以理解数学目标，掌握数学知识的产生背景，确切的挖掘数学知识概念、数学知识定理和数学知识法则，深度探索数学知识的思想方法，理解各知识点的多元化管理.感悟数学知识的内涵与理性精神，区分核心知识与非核心知识，切合实际的归纳知识生成背景，还要思考是否能够利用和类比以及推广数学知识.

1.2 理解学生

学生是学习的主人，需要在自主学习过程中不断提升自己.初中学生学习是相对活跃的个性化成长过程，积极研究和动手实践均是数学课堂学习的主要方式.给学生提供充分的时间去猜测、计算以及验证，学生认真思考总结知识产生规律，这些均需要建立在教师精心设计教学活动基础之上，由此发展学生知识技能与情感态度价值观.

1.3 理解教学

教学活动的本质是师生交流互动以及共同发展的一个过程，良好的教学活动，应该是教师教和学生学之间的和谐统一.学生是课堂学习的主体，教师通过发挥自身组织者、引导者职能开展教学活动，要调动学生学习兴趣，激发学生主观能动性，带领学生积极思考、乐于探索、勇于创造.让学生潜移默化地掌握科学的学习方法，从而促进学生良好学习习惯的养成.在课堂教学实践中强调学习内容之间的关系挖掘，通过学习探究活动，带领学生经历知识发生与发展的过程，系统地构建数学知识结构体系，丰富学生学习经验.基于此，初中数学就是认真掌握理解数学、理解学生和理解教学的关系，落实学生探究能力的培养.

2 初中数学教学中培养学生探究能力的策略

目前，依旧存在诸多学生过度关注卷面成绩，追求高分数学的错误的学习思想，通过刷题方式，提高学习成绩，把考试当作自身学习的终极目标.大量的课业负担影响着学生探究习惯的养成，长时间之后会降低学生探究热情，无法培养学生的综合能力.目前的初中数学教学中，学生探究能力培养依旧需要进一步探索，要为学生健康成长与个性发展提供有利条件.

2.1 树立学生探究意识，积极正确引导

在培养学生探究能力过程中，就要意识到探究能力的培养并不是盲目探究，而是有针对性地组织学生参与探究活动.在实际的教学中，首先要引导学生树立正确的探究意识，给学生设置合理的情境，引导学生从中探究，有目的的提出解决问题方案，做好培养学生的探究活动的准备.比如在学习“有理数乘方”时，可以设置以下探究活动：一张厚度为1 mm的硬纸板对折一次有多厚？对折两次有多厚？对折三次呢？对折10次呢？有人说一张厚度为1 mm的硬纸板（足够大）对折24次后，比珠穆朗玛峰还要高，可能吗？这样的问题情境设置，一方面具有悬念，激发学生探究新知的兴趣;另一方面学生能动手操作，便于探究规律.通过教师的有形引导，充分调动学生自主探究意识，便于学生全方位理解数学知识，在数学课堂中得到良好的学习体验.

2.2 实施多元理念，落实因材施教

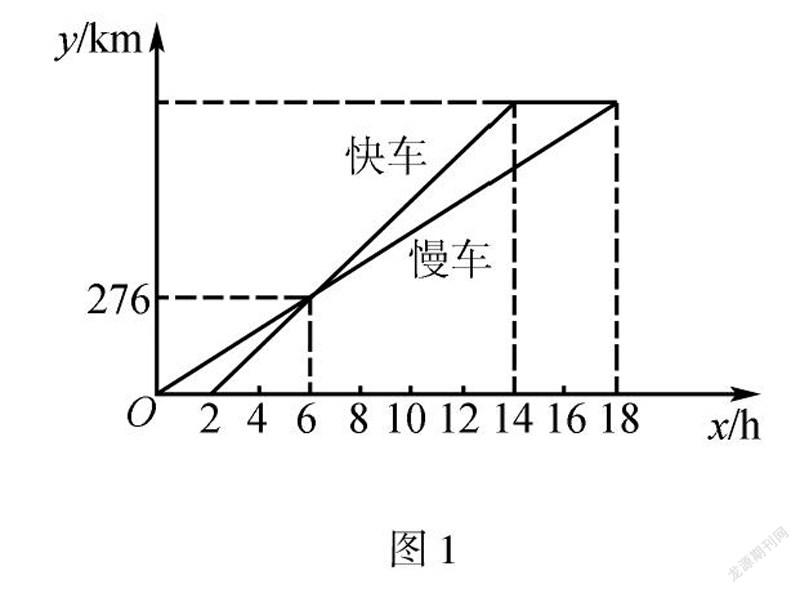
作为相对独立的个体，学生和学生之间存在显著的个体差异，因此在数学教学活动中，教师应保持客观性与公正性，公平对待每一位学生，不要单一的关注学生学习成绩，更要关注学生综合学习能力的培养.教师也应按照因材施教原则进行教学活动，为学生个性成长提供便捷条件.在学习“用一次函数解决问题”时，设计这样一个问题：一辆慢车和一辆快车沿同一条公路从苏州（A）到无锡（B），所行的路程y（km）与时间x（h）的函数图像如图1所示.

（1）快车比慢车晚出发_______h，慢车比快车晚________h到达B地;

（2）快车经过________h追上慢车，快车行驶了_________km追上慢车;

（3）求慢车、快车的速度;

（4）求A、B两地之间的路程;（5）慢车出发多少小时两车恰好相距46km？

为了让每一位学生按需学习，让不同的学生在数学上获得不同的发展，前四小题是基础题，可以帮助学生深化基础知识内涵.对于学有余力的学生增加第5小题加以拓展，让这部分学生不断地发挥自我潜能，完成探究学习任务.

2.3 激发学生学习兴趣，增强探究欲望

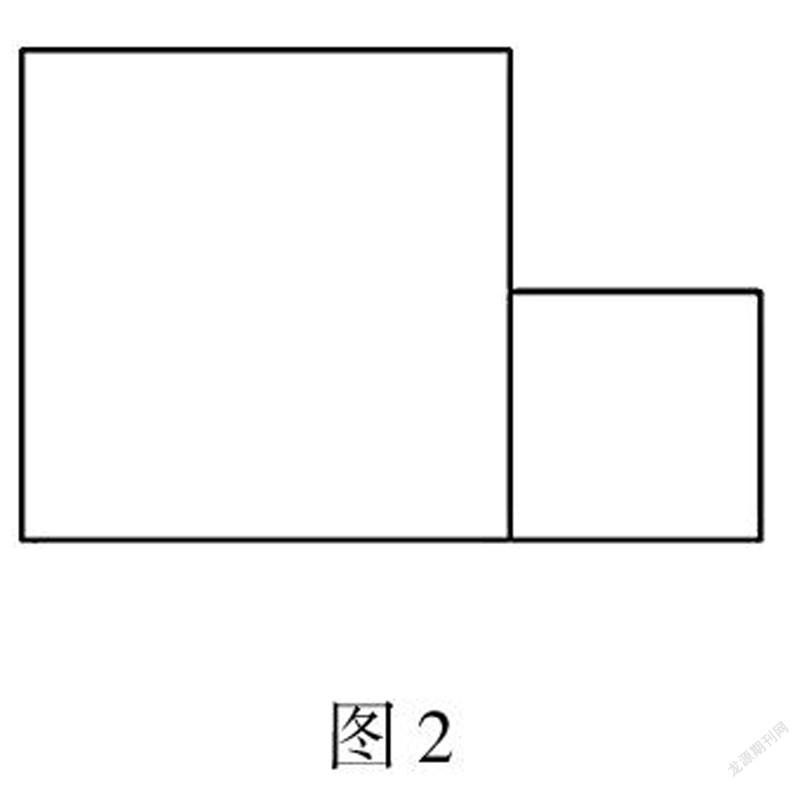
教师应该关注学生学习兴趣的激发，把学习兴趣的培养，当作学生学习效率提升的关键手段，集中学生学习注意力，能够引导学生全方位了解数学知识，生成探究心理.教师需要做好充分的教学准备，课堂上激发学生学习热情，在课后注重教学与学习巩固之间的过渡，实现初中学生深层次学习.比如在学习“勾股定理”时，设置如下问题情境：如图2，两个边长不同的正方形連在一起，请你剪两剪刀，再把所得图形拼成一个正方形.

通过这样的问题情境，为学生提供了一个有趣而又富有挑战的问题，激发学生学习本节内容的兴趣，提高了学生自主探究的热情.学生带着问题学习本节课的内容，又用本节课的知识解决此问题，让学生领悟到探究的乐趣，品味到成功的快乐.同时此问题又是证明勾股定理的方法，为下节课勾股定理的证明做铺垫.

2.4 变式延伸，发展学生思维能力

在教学中，一些问题看上去不同，但究其本质却相同，解题思路和方法一致，教师在平时的教学中要注意积累，引导学生加以比较，并且寻找此类问题之间的内在联系，从而寻求通法通解.变式延伸，不但可以解决一个问题，而且可以解决一类问题，避免“题海战术”的同时，也拓宽了学生思维广度，增强了学生的探索意识，发展了学生的思维能力，实现“以少胜多”.比如研究“圆外一点与圆上一点的距离最值”时，设计了以下习题：

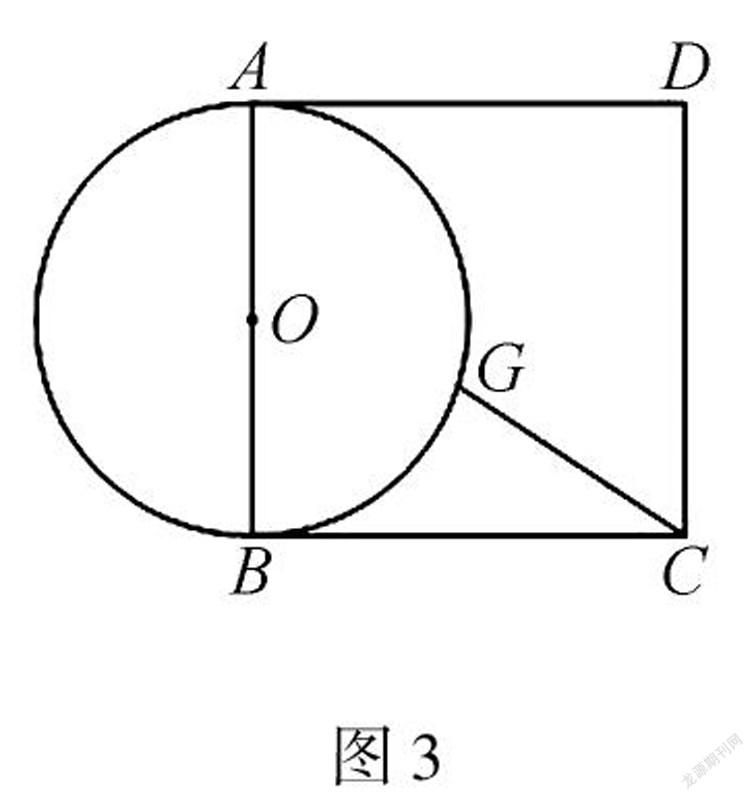
例如，如图3，已知边长为2的正方形ABCD，圆O是以AB为直径的圆，G 是圆O上的一个动点，连接CG，求CG长的最小值.

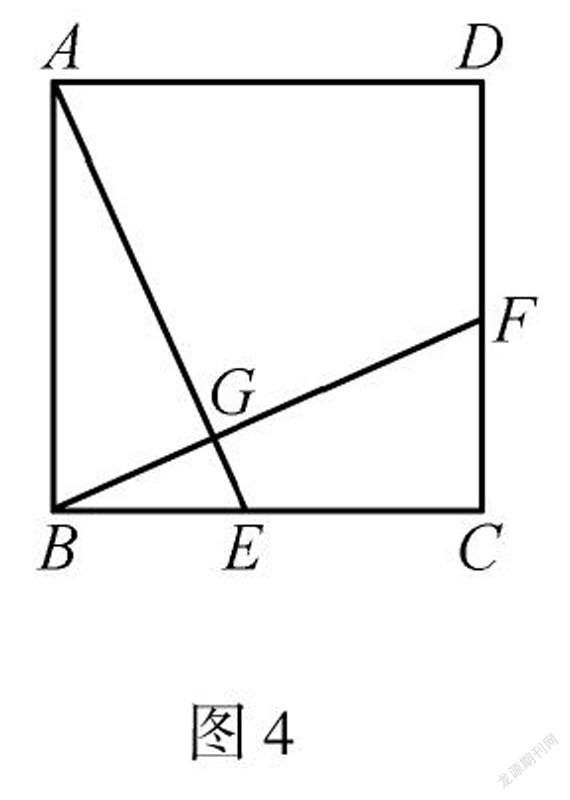
变式1如图4，已知边长为2的正方形 ABCD ，E、F分别是边BC、CD上的点，BE=CF，AE、BF相交于点G，求CG的最小值.

变式2如图5，在Rt△ABC中，∠ABC=90°，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，求线段CP长的最小值.

将问题进行迁移变式，逐步探究圆外一点与圆上一点的距离最值，有利于学生解题思想方法的形成和巩固，达到了理解掌握该问题的目的.通过变式延伸，让学生触类旁通，在提高学习效率的基础上，开拓了学生思维的深度和广度，培养了思维的灵活性和变通性.

综上所述，初中数学是一门抽象性与逻辑性相结合的学科，对学生探究能力的培養尤为重要.新课改标准下，数学教师应关注学生的探究能力的提升，通过小组合作与多元化的教学思想，潜移默化地树立学生探究意识，调动学生学习热情，鼓励学生及时进行课后总结和反思，整理完整的数学知识结构.采取高效的措施，如树立学生探究意识，积极正确引导;实施多元理念，落实因材施教;激发学生学习兴趣，增强探究欲望;关注合作探究，发展学生探究能力;变式延伸，发展学生思维能力，鼓励学生在今后的学习中勇于面对困难，积极进取，强化学生数学学习能力与核心素养.

参考文献：

[1] 李强.基于核心素质培养下初中数学学生自主探究的尝试与思考[J].考试周刊，2019（7）：85.

[2] 李毅，杨文.初中数学课堂引入方式的探究[J].读与写（教育教学刊），2019，16（1）：111-112.

[3] 沈娟.探究式教学模式在初中数学教学中的应用[J].数学教学通讯，2019，678（5）：49-50.

[责任编辑：李璟]