轴箱振动计算轨道不平顺方法研究

汪忠海，罗晋楠，张济民

（1.中车长春轨道客车股份有限公司上海工程技术研究中心，上海 310112；2.同济大学铁道与城市轨道交通研究院，上海 201804）

1 概述

轨道不平顺指的是轨道的尺寸、形状与理想位置的偏差[1]。它可以分为几何不平顺和弹性不平顺，几何不平顺是指线路上没有车辆运行工况下，轨道自身的不平顺，而弹性不平顺指线路上由车辆运行的工况下，轨道产生的不平顺。轨道不平顺状态对车辆运行时的舒适度、噪音、安全等都有着重要的影响[2]。

目前，计算轨道不平顺的方法主要有2种：惯性基准法和弦测法[3]。惯性基准法主要是根据获取的加速度值换算成轨道的不平顺位移，包括惯性位移法、轴箱加速度积分法等。弦测法主要是根据对位移量的测量结果换算出轨道不平顺的位移，包括两点差分法、三点中弦法等。国内外根据这些方法和原理，采取了不同的方式实现对轨道不平顺的测量。当前，国内外已经开发出一些测量轨道不平顺的设备[3−5]，如：德国的mbbmRM1200E，该设备安装有多个接触式探头，设备沿轨道移动时探头获取钢轨外形数据测量轨道不平顺。但是该设备使用时需要缓慢推行，测量速度较慢；英国的CAT（Corrugation Analysis Trolley）测量设备，在小车上安装加速度测量装置，小车沿轨道行驶时测量与轨道接触的加速度，经过换算从而得到轨道不平顺，这种测量方法有测量快速、使用便捷等特点；我国的GJ−4 型检测系统，通过激光摄像组件、加速度传感器等部件采集的数据进行综合分析，得到轨道不平顺。

图1 国外轨道不平顺检测设备Fig.1 Foreign Track Irregularity Testing Equipment

基于轴箱加速度对轨道不平顺的状态进行计算进行研究。通过惯性基准法，利用在车辆轴箱上安装传感器所测得的加速度，计算出轨道的不平顺数据。通过惯性基准法测量得到的不平顺数据是轨道的弹性不平顺，其本质上是列车受到轨道不平顺激励之后轮对的位移，相比于使用轨道检测设备检测得到的轨道几何不平顺数据，弹性不平顺对线路和车辆的评估更具有参考意义。同时该方法可以实现对整条运营线路的快速检测，具有成本优势和效率优势。

2 数学模型

轨道的不平顺其本质上是一个随机过程，是里程的随机函数[6−5]。轨道不平顺通过轮轨刚性接触向上传递所激发出轴箱的振动，是一种随机振动[7]。轨道车辆一般使用刚性轮对，轮对自身刚度较大，车轮和轨道之间近似看作为刚性接触[8]，即钢轨的不平顺偏移能够直接的传递到车体的轮对和轴箱上，因此通过对轴箱加速度的换算可以得到轨道的不平顺。目前可以加速度到不平顺的计算主要分成两种方法，一种是在频域上对加速度信号进行处理并计算成频域上的位移信息，再变换回时域；另一种是在时域上直接采用积分方式将加速度信号换算成位移信息。

基于频域的轨道不平顺计算方法，将轴箱加速度的时域信号转换成为频域的信号，通过计算可以得到频域上的位移信号。假设采样得到的离散随机加速度信号为a（n），n=1，2……N−1。

首先通过快速傅里叶变换变换，可以将时域的a（n）信号换算成频域信号A（k）：

k=0，1，2……（N−1），k点的频率为：

式中：N—采样点数；F—采样频率。

根据时域中积分法在频域中对应的实现方法，可以将频域中的加速度信号A（k）经过两次积分得到位移的频域信号Y（k）：

在对车体进行频域的动力学计算或分析时，可以使用Y（k）作为频域的轨道谱，如果需要时域的结果，可以通过傅里叶逆变换从而计算得到，并且由于计算使用复数域进行计算，因此在逆变换时不会丢失相位信息：

基于时域的轨道不平顺计算方法，与频域法近似，当获取到轴箱加速度后，可通过时域上两次积分从而获得假设采样得到的离散随机加速度信号为a（n），n=1，2……N−1。

首先通过离散积分将加速度信号转化为速度信号，之后再进行一次积分转化成位移信号。对于离散点的数值积分方法有很多，如：中点公式，梯形公式，辛普森公式，复合辛普森公式等。

本文中以辛普森公式为例对离散信号进行分析。辛普森（Simpson）公式又称为抛物型公式，其表达式为：

辛普森公式计算的误差R［f］为：

其中，ξ∈(a,b)。

辛普森公式为3次代数精度的求积公式，即对于3次及以下次数的多项式，辛普森公式能够保证其没有误差。对于测量得到的振动数据，其实质是一种随机函数，因此使用辛普森积分必定存在误差。但是辛普森公式相比于中点公式梯形公式，其代数精度较高。对于离散积分而言，代数误差是不可避免的，综合考虑到计算复杂性和误差大小，一般使用辛普森公式进行离散积分。辛普森公式其本质相当于对当前计算的点和该点的前后点，共三点进行二次插值拟合，然后根据拟合后的函数进行积分计算，并对信号中每个点都进行该操作从而实现整体数据的积分。对原始信号使用更高阶的公式进行离散积分，反而可能会由于对离散点的过拟合导致积分结果不准确。将a（n）两次带入辛普森公式，如式（7）所示。

式中：t—采样间隔；v（k）—离散速度；y（k）—离散位移。

使用加速度传感器进行积分时，加速度的误差会累计，当速度积分成为加速度时，误差会再次累计，累积的误差会导致计算得到的位移产生连续的偏移，即趋势项[9]。轨道不平顺的值本应是离散的随机函数，积分后的结果不应产生趋势项，因此需要对积分计算得到的位移函数进行修正，去除其趋势项。在实际操作中，可以在计算v（n）和y（n）积分后时分别去除其趋势项，但是其实质与在y（n）处去除一个包含更高阶次的趋势项等效。这里直接去除y（n）的趋势项，设定趋势项阶次为4阶。设趋势项δ的表达式为：

通过最小二乘法拟合y（n）确定A的值，如式（9）所示：

其中，

去掉趋势项后即可得到修正后的结果，即轨道的不平顺位移：

对加速度度信号积分后对计算结果进行滤波也可以消除加速度信号的误差积累[10−11]，而文中使用通过对积分曲线拟合去除趋势项的方法。两种方法的目的都是为了去除加速度仪器测量时积累的误差。此外，经过两次积分后，理论上得到的位移信号和加速度信号会有180度的相位差，由于轨道的不平顺是一组随机序列，其中包含多个频段，其波长不同，不同频段的信号积分后因为相位差所导致的偏移量不同，因此也会造成一定程度上的误差，但是该误差仅在时域上体现，不会对功率谱的分析造成影响。

3 实验及数据处理

为验证第一章节所描述的两种方法，在某大学轨道交通试验线上进行实验。本章主要介绍实验数据的获取和测量数据的预处理。实验数据获取，在试验线轨道车辆模型的轴箱上安装无线加速度传感器进行实验，该车辆结构和传感器安装位置，如图2所示。

图2 轨道车辆模型Fig.2 Rail Vehicle Model

正式测试前，将车辆模型静置，记录一组车辆不工作状态时的加速度信息。然后，控制模型车辆电机按照恒定速度行驶，当模型车启动至平稳运行后，开始记录数据。

实验数据预处理，在加速度传感器使用时，由于传感器自身的元器件属性，设备和周边环境等因素的影响，传感器自身存在一定的零点漂移和噪声误差。若不对零点漂移进行处理，在两次积分的过程中将势必产生严重的误差累积。因此在使用加速度测量结果计算轨道不平顺前，需要对数据进行预处理以减少传感器的误差，滤除无效的数据。方框框出的部分即为车辆静止状态下测得的数据，右端为车辆启动后的加速度信息，如图3（a）所示。当车辆静止时，实际测得信号均值发生了明显的偏移，加速度信号均值为不为零，即发生了零点漂移。

图3 数据处理前后加速度信号Fig.3 Acceleration Signal Before and After Data Processing

在对运行加速度的信号处理时，需要首先去除传感器的零点漂移，即将车辆稳定行驶后测量的数据减去对应静止时测量得到的加速度平均值。选取一段稳定运行后的数据进行处理，结果，如图3（b）所示。

4 轴箱加速度信号分析

根据第二章的时域和频域计算方法，分别对测量的加速度进行计算。通过时域法对轴箱加速度信号进行积分的结果，如图4所示，虚线表示两次积分后的位移，实线表示对该位移进行四次多项式拟合得到的趋势项，横坐标为采样点数。对轴箱的垂向加速度计算得到的结果，如图4（a）所示。对轴箱横向加速度计算得到的结果，如图4（b）所示。

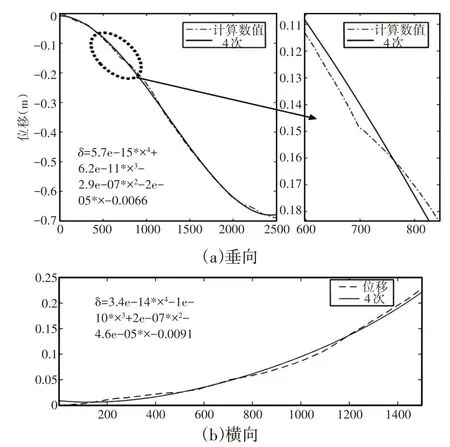
图4 位移积分结果及拟合曲线Fig.4 Integral Result of Displacement and Fitting Curves

可见，即使将信号的零点漂移去除，对加速度传感器采集到的信号进行积分的过程中依旧会产生误差的积累，因此在进行过零点漂移的修正后，去除趋势项造成的误差也是有必要的。图4中δ即通过式（9）计算得到的趋势项与对应采样点之间的关系，将计算数值减去对应拟合结果进而得到不平顺的修正结果，如图6中实线所示。

将同一段数据通过FFT转换到频域上进行计算，得到加速度和位移结果，其功率谱，如图5所示。图5（a）为轴箱垂向加速度的频域数据，图5（b）为同一时刻轴箱横向加速度的频域数据。

图5 频域法中加速度和位移的FFT图像Fig.5 Acceleration and Displacement FFT Result Calculated in Frequency Domain

频域和时域内的计算结果对比，如图6所示，其中图6（a）是轨道横向不平顺位移，图6（b）是轨道垂向不平顺位移。实线是在时域内计算的结果，虚线是在频域内计算的结果。不难发现，时域和频域上的计算结果不平顺幅值相近，但不平顺分布具有一定的差距，特别是横向加速度计算得到的结果相差较大，且在频域计算得到的结果其不平顺主要集中于低频部分。这是因为在频域中将加速度积分成位移信号的过程中，如式（3）所示，每个频率对应的信号乘以转换系数得到对应频率下的位移信号。

对于高频信号对应的系数很小，而低频信号对应的系数则非常大。由于采样点是离散的，采样的过程中会造成真实数据的丢失，在对频域信号进行积分的过程中，放大的信号不是真实的信号而是丢失了部分数据的采样信号，最后导致积分的结果并不精确，所以通过频域计算的结果中信号低频能量较大，而高频信号能量较低。将频域的计算结果在反演回时域的信号后，信号的中高频成分较少，如图6虚线所示。实验结果表明，相比于在时域上进行积分计算，频域的计算效果不佳。

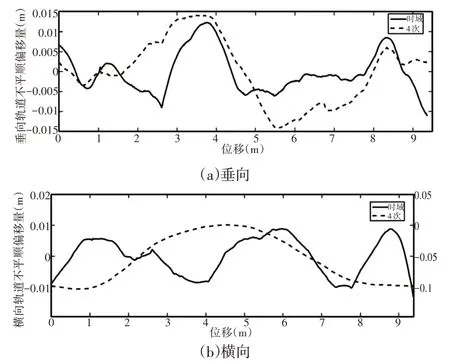
图6 轨道不平顺位移计算结果Fig.6 Track Irregularity Result Calculated in Time and Frequency Domain

影响列车动力学性能的频率主要分布在低频频段，若计算出轨道谱的低频信号发生失真，对会大大影响后续车辆动力学分析的准确性，建议在时域上计算轨道不平顺。

5 结语

这里根据轴箱上的加速度信号，分别在时域和频域内进行积分计算得到了横向和垂向的轨道不平顺。经试验表明，轴箱上的加速度信号经过处理后能够较好的反映出车辆行驶所经过轨道的不平顺信息，并且在时域上通过积分和去除趋势项计算得到的轨道不平顺相比于频域上的计算结果更加可靠，对车辆和线路的评估具有重要参考意义。