图像清晰度的小波变换抗噪评价算法

武钰瑾，赵凤霞，辛传福，牛森涛

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

机器视觉系统已广泛应用于各个领域，获取清晰图像是保证机器视觉系统精度的前提。在调焦过程中，清晰度评价是不可缺少的部分，对清晰度的准确评估能够获得丰富的信息量，为物体尺寸测量等提供大量数据[1]。为了给调焦系统提供优良的评价依据，要求清晰度评价算法在调焦过程中的计算结果具有无偏性、单峰性、高灵敏度与高效性。

小波变换是现有的一种能够反映图像内在特性且能够与人类视觉特点相契合的分析方法和表征工具。它是一种具有多分辨率的信号分析方法，可在时域与频域中表征信号的局部特征，能够从信号中提取有效信息。许多学者基于小波变换对图像的清晰度进行评价。其中，文献[2]通过二维离散小波变换对其三层高频子带的对数能量进行计算，获得图像清晰度评价，文献[3]运用提升小波变换提出一种将高、低频信息相结合去噪的调焦评价算法；文献[4]通过构造原始模糊图像的参考图像，基于局部离散小波变换对原始模糊图像和参考图像的高频能量图的相似度进行对比，得到原始模糊图像的质量；文献[5]提出在通过小波变换在纹理方向即小波变换的高频子带方向加以不同的权重得到图像的清晰度评价结果；文献[6]通过对图像的显著区域采用FISH算法进行计算得到一种清晰度评价算，上述学者的主要思想是对图像中高频细节能量进行计算。这里基于二维离散小波变换，通过对其高频系数的变化快慢进行计算，对图像清晰度进行评价，与传统算法相比，该方法能够很好的避免噪声的影响，得到的评价结果具有较高的准确性和灵敏度。

2 算法原理

2.1 基于小波变换高频系数的清晰度评价算法

工业相机对图像进行采集时，镜头系统相当于一个低通滤波器，当截止频率高时，能够聚焦准确，采集到清晰图像，截止频率低时，会产生较大的散焦量，采集到的图像会比较模糊，所以图像的模糊是由于图像在频域中的高频分量的流失[7]。小波函数能够对信号的高频部分与低频部分进行分离，对图像细节信息进行多尺度的细化[8]。二维小波变换的分解过程，如图1所示。

图1 二维小波变换的分解过程Fig.1 Decomposition Process of Two−Dimensional Wavelet Transform

图1 中，输入图像分别与低通滤波器hφ(−n)和高通滤波器hψ(−n)做卷积，并对结果进行抽样，得到两个水平分辨率以2为因子下降的子图像，然后对两个子图像分别通过hφ(−m)和hψ(−m)进行滤波并抽样，获得四个四分之一大小的图像，即一个低频模糊图像，三个高频细节图像。

尺寸为M×N的图像f(x,y)的二维离散小波变换可定义为：

式中：Wφ(j0，m，n)—在尺度j0上f(x，y)的近似值；W ψi(j，m，n)—水平、垂直和对焦方向的细节系数；h、d、v—水平、垂直和对角方向；j0—任意开始变换的尺度；m、n—位移因子。

一般地，小波变换的高频系数会随着图像的清晰而出现明显的跃变。因此，图像的清晰度可用高频系数的梯度进行表示。其定义如下：

式中：Gm,Gn—高频系数在m方向和n方向的梯度。

梯度的幅度表示了高频系数变化的情况，当图像比较清晰时，梯度的幅度值比较大。

根据导数的定义，式（3）可以转化为式（4）：

图像的三个高频子图分别体现了图像的水平、垂直与对角方向的细节特征，因此，这里提出采用梯度平方法对三个方向的高频系数的变化快慢进行评价，评价表达式如下：

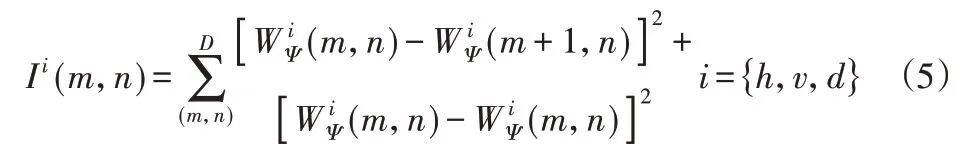
式中：D—i方向所有高频系数的集合；(m,n)—图像中某高频系数的位置，h、d、v为水平、垂直和对角方向。

综合考虑水平、垂直、对角三个方向的清晰度，得到图像的清晰度评价函数：

式中：α、β、γ—加权因子，根据图像纹理方向特征可调整其权重大小。

2.2 小波变换分解层数的选取

小波变换在分解图像信号时，通过P组滤波器产生尺度为j0−1, j0−2,...,j0−P的P尺度高频与低频系数，低尺度系数（如j0−2）是基于高尺度系数（j0−1）获得的，其过程，如图2所示。

从高尺度向低尺度分解是通过对高尺度的低频信息进行分解，获得低尺度的高频信息与低频信息，然后再对低尺度的低频信息进行分解，获得更低尺度的高低频信息。

低尺度信息舍去了高尺度分解获得的高频信息。由于噪声属于高频信息，在待测图像存在较多噪声时，仅进行一层分解获得的高频系数易受到噪声影响，但在进行清晰度评价时，又需要考虑较高尺度的细节。为了保证不丢失过多细节的同时降低噪声的影响，在噪声影响较大时可选择较高层变换的高频系数，在较少噪声的情况下可选择较低层小波变换的系数。

3 算法验证

这里采用大恒MER−503−36U3C工业相机对平铣样块进行连续变焦采样，获取了三十张图片参与实验（部分样块图像，如图3所示，图片分辨率为504*500），同时给这组图片加入均值为0，方差为0.01的高斯白噪声作为一组含噪样本参与实验，如图4所示。基于Matlab R2018a，采用这里所述方法对分解层数为1、2、3、4、5层的小波变换高频分量进行清晰度评价。评价结果，如图5所示。

图3 部分未加噪声的实验图像Fig.3 Some Experimental Images without Noise Added

图4 部分加入高斯白噪声的实验图像Fig.4 Some Experimental Images with Noise Added

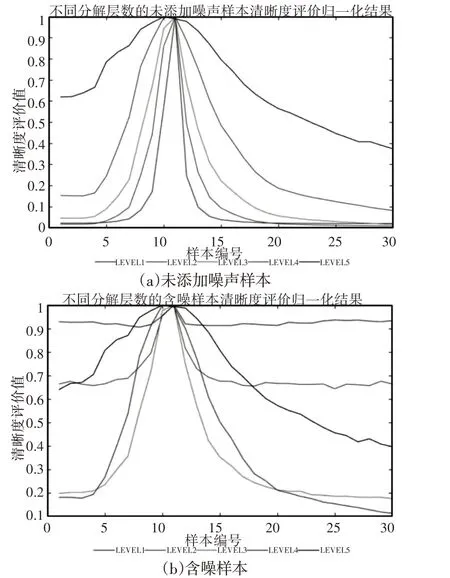
图5 不同分解层数对样本的清晰度评价结果Fig.5 Evaluation Results of Sample Clarity with Different Decomposition Levels

由图5（a）可知，在未添加噪声的样本中，分解层数越低，清晰度评价算法的灵敏度越高，当分解层数达到5层时，评价算法的清晰度评价将偏离正确的对焦位置，出现对焦不准确的现象。其主要原因为，分解层数越高，其高频细节信息含量越少，当分解层数达到一定值，其高频信息描述的细节信息过少，将失去对清晰度评价的能力。但在添加噪声的样本中，由于噪声属于高频信息，分解层数越低，其中含有的噪声分量越多，清晰度评价的稳定性越容易受到噪声的影响。如图5（b）中所示，仅进行一层或二层分解在离焦位置，将出现多个局部极值，无法判断对焦方向。综上所述，信噪比较低的情况下选取小波变换的第三层高频系数进行清晰度评价能获得较为满意的结果。但在信噪比较高的情况下，可选择低层高频系数进行清晰度计算，以获得较为灵敏的评价结果。为了验证这里算法的优越性，对两组样本分别采用梯度平方法、FISH算法[2]、variance函数法以及这里提出的算法进行清晰度评价并将评价结果归一化，结果，如图6所示。

图6（a）中，选择第2层小波变换高频系数进行计算，四个评价算法均具有较好的单峰性，但variance函数出现了对焦不准确的情况，且variance函数对图像清晰度评价的灵敏度较低。梯度平方法在清晰图像附近的灵敏度较好，离焦位置处，FISH算法灵敏性较好。但从整个对焦过程来看，这里提出的算法灵敏度更佳。图6（b）中，选择第3层小波变换高频系数进行计算。由于样本中添加了噪声，四种算法对图像清晰度的评价均受到了影响。但variance 函数受到的影响最小，仍具有单峰性，未出现局部极值，但其仍存在对焦不准确的情况。梯度平方法与FISH算法的评价结果均受到了较大的影响，出现了多个局部极值，在离焦位置清晰度评价波动较大，无法指导对焦方向。这里提出算法也出现了局部极值，但噪声的出现对清晰度评价结果整体的影响较小，仍具有较高的灵敏度，且对焦位置准确。

图6 不同评价算法对两组样本评价归一化结果Fig.6 Normalized Results of Two Groups of Samples Evaluated by Different Evaluation Algorithms

两组样本通过FISH算法、variance函数法、梯度平方法以及这里提出算法进行清晰度评价的运算时间，如表1所示。由表中可见，FISH算法运算速度慢，variance算法与这里提出算法运算速度相当，梯度平方法运算速度最快。四种算法均可满足实时性需求。

表1 清晰度评价算法运算速度Tab.1 Three Sets of Samples Clarity Evaluation Operation Speed

4 结论

这里通过二维离散小波变换，对图像中高低频信息进行分离，根据高频系数的变化速度快慢，提出了一种图像清晰度评价算法。同时采用工业相机，对平铣工件表面图像进行连续变焦取像，作为一组实验图像，并对该组图像加入均值为0，方差为0.01的高斯白噪声作为含有噪声实验图像。对这两组样本，采用不同分解尺度的高频系数获得的清晰度评价值进行比较，经过实验验证，高信噪比图像中，低层高频系数的评价结果具有较高的灵敏度，但对低信噪比图像的评价稳定性将会减弱。经过三层小波变换获得的高频系数具有较好的评价精度与评价灵敏度，同时具备较好的抗噪能力。

对高信噪比样本与低信噪比样本通过采用较为广泛的FISH算法以及梯度平方法、variance函数和这里提出的评价算法进行评价效果测试。经过实验验证表明，variance函数灵敏度较低，且不满足无偏性要求，但抗噪能力较强；梯度平方法与FISH 算法对低信噪比图像的评价中存在多个局部极值，这里提出的算法具有无偏性，具有较高的灵敏度，同时具有较好的抗噪能力，能够作为调焦函数应用在调焦过程中。