输电塔单变双角钢过渡节点试验研究与计算方法

徐再根，郑为东，刘俊才，刘文棚，田 利

(1. 山东电力工程咨询院有限公司，山东济南 250013； 2. 山东大学土建与水利学院，山东济南 250061)

0 引 言

“特高压”是中国重点发展的新型基础设施建设项目之一，是未来一段时间内电力行业重点关注的课题。特高压输电线路具有空间跨度长、输电容量大和架设塔体高等特点，在外界环境荷载(大风荷载、覆冰跳跃、地震作用、断线冲击等)下的非线性振动响应尤为显著，传统的单角钢截面主材已无法满足输电塔的强度设计要求。在特高压输电塔实际工程中，为了满足承载要求并提高板件利用率，通常将输电塔受力较大的底部主材更换为组合双角钢截面。由于单变双角钢过渡节点中连接水平板的上、下靴板中心线不重合且存在不可忽略的偏心距离，导致从单角钢主材向双角钢主材的传力路径复杂且不清晰。由于《架空输电线路杆塔结构设计技术规定》[1]和《110 kV～750 kV架空输电线路设计规范》[2]中未给出统一的计算方法进行指导，目前在过渡节点的结构设计中，通常根据设计经验增大水平连接板件的厚度，导致浪费大量的耗材成本和加工成本。因此，研究过渡节点的受力特点和承载性能对过渡节点的结构设计和优化具有重要意义。

单变双角钢过渡节点是满足角钢塔更高承载要求的一种新型节点形式，目前仅有少量学者对过渡节点的受力特性开展研究。黄宗明[3]以单角钢连接节点板为研究对象开展了足尺试验，并通过有限元模拟方法研究了节点板的破坏机理及破坏模式。程睿等[4]开展了单角钢连接节点板的足尺试验，提出了节点板受压承载力的计算方法。李光照[5]通过电测技术研究了10种不同构造形式，共24个常用双角钢杆件桁架外加式焊接节点板的原型试验，得到了节点板破坏机理并提出相应的设计原则。杨利容等[6]分析了过渡节点的受力情况，并验证连接板件满足安全要求。鞠彦忠等[7-8]研究了钢管-角钢过渡节点的极限承载力，并与现行规范进行对比，分析了不同参数对极限承载力的影响程度。陈旭阳[9]基于近似平面假定理论推导了过渡节点水平连接板厚度的计算方法，并通过数值模拟和真型试验验证了计算方法的正确性。朱昌建等[10]建立不同尺度的过渡节点模型，研究了不同参数对过渡节点力学特性的影响规律。杨垂玮等[11]通过研究过渡节点的传力机理，明确影响水平连接板受力情况的控制因素。Yam等[12]发现当水平板上的荷载增大到一定程度后，水平板出现屈服且内力发生重新分布。Sheng等[13]提出了一种非弹性受压性能和强度的研究方法，参数化分析了水平板承载力的变化情况。薛晓敏等[14]通过仿真计算探究了节点在拉压荷载作用下的受力机理和破坏模式，并基于屈服线法理论提出单变双角钢关键节点整体承载力设计推荐公式。开展单变双角钢过渡节点加载试验是研究其承载性能最可靠的方法，然而目前的相关研究主要基于数值模拟和理论分析，鲜少涉及过渡节点加载试验。

基于上述的研究背景与现状，本文依托某特高压输电线路实际工程，选取3个典型的单变双角钢过渡节点为研究对象，开展过渡节点数值模拟和加载试验，研究其在受拉和受压工况下的承载性能和受力情况，为过渡节点的结构设计提供参考。

1 试验概况

1.1 试件设计与制作

基于特高压输电线路实际工程，选取3个单变双角钢过渡节点为研究对象，共制作8个过渡节点试验模型，其中6个足尺试验模型分别在受拉和受压工况下进行弹性加载试验，2个缩尺试验模型分别在受拉和受压工况下进行破坏加载试验，过渡节点试验模型如图1所示。根据缩尺理论将过渡节点的几何尺寸按照缩尺比例1∶2进行设计，其他相关参数按照量纲分析法进行确定。鉴于本文的研究重点为单变双角钢过渡节点连接板件的强度和稳定问题，为了防止角钢构件先于连接板件发生破坏，适当增大了缩尺试验模型中单、双角钢构件的厚度，过渡节点试验模型的尺寸参数如表1所示。各过渡节点的角钢构件、5E3-SJC4节点的水平板和靴板采用Q420钢材，其余构件采用Q355钢材，角钢与靴板之间采用8.8级的高强螺栓进行连接，且足尺与缩尺模型螺栓型号分别为M24和M12。由于输电塔主材沿塔身高度存在倾角，在加工试验模型中，单角钢与水平板的夹角为87°(93°)，双角钢与水平板的夹角为93°(87°)。节点试验模型与加载装置及反力架的组装如图2所示。

图1 足尺与缩尺过渡节点试验模型Fig.1 Full-scale and Scale Transition Joint Test Models

图2 节点组装Fig.2 Joint Assembly

表1 试件尺寸及加载工况Table 1 Specimen Dimensions and Loading Conditions

1.2 加载制度及测点布置

本次试验采用MTS液压伺服加载系统进行加载。试验采用分级加载[15]形式进行，荷载控制方式采用力控制，加载速率为1 kN·s-1，每级加载保持5 min。受限于试验条件和仪器吨位等因素，弹性和破坏试验的受拉工况设计荷载为640 kN，受压工况设计荷载为940 kN。弹性试验的加载级别为设计荷载的0%、30%、50%、75%、100%；破坏试验的加载级别为设计荷载的0%、30%、50%、75%、90%、95%、100%，加载方式如图3所示。此外，在进行正式加载之前，对过渡节点试验模型均进行预加载，预加载分2级进行施加，每级加载值为设计荷载的10%，加载速率和保持时间同正式加载，加载完毕后以10 kN·s-1的速率进行卸载，预加载用以保证试验模型安装的合理性和加载系统的稳定性。

图3 试验加载制度Fig.3 Test Loading System

由于上、下靴板与水平板的连接焊缝存在不可忽略的偏心距离，当荷载从上靴板传至下靴板时，在水平板上产生较大的偏心力矩，该偏心力矩是影响水平板受力的主要因素[9]。为了记录不同加载级别下过渡节点试验模型的受力情况，在上、下靴板与水平板的相交区域附近布置数个应变片和应变花，过渡节点试验模型的应变测点布置如图4所示，其中H代表应变花，P代表应变片。

图4 应变测点布置Fig.4 Layout of Strain Measuring Points

1.3 材性试验

过渡节点试验模型加工过程中，按照《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975—2018)的相关要求，在上、下靴板和水平板母材上预留样坯，根据《金属材料室温拉伸试验方法》(GB/T 228—2002)[16]对样坯加工成形并进行单向拉伸试验。材性试样共分为8组，每组加工3个试件，图5给出了材性试验尺寸信息，试样长度分为A、B两类，图6为材性试样实物。材性试验主要测定项目包括钢材的屈服强度、极限强度和伸长率等，每组结果取3个试件的平均值并列于表2。

图5 材性试样尺寸(单位:mm)Fig.5 Dimensions of Material Property Samples (Unit:mm)

图6 材性试样照片Fig.6 Picture of Material Property Samples

2 有限元模型验证与试验结果分析

2.1 有限元分析模型

在ABAQUS有限元软件中采用C3D8R实体单元建立单双角钢过渡节点精细化模型，由于缩尺试验模型(5E3-SJC4-SC)是基于足尺试验模型(5E3-SJC4)按照1∶2的缩尺比例进行设计，图7仅给出了编号为5E3-SJC4、5E5-SJK2A和5E5-SJ4A的过渡节点有限元模型。材料本构采用理想弹塑性模型，构件材料参数采用表2中材性试验的测定结果。水平板与加劲板、靴板的连接焊缝采用“Tie”模拟，螺栓与连接板件的相互作用采用硬接触和摩擦接触，其摩擦因数取0.15。在对过渡节点加载之前，先在螺栓杆中施加螺栓预紧力[17-18]，共设置3个分析步，第一分析步对螺栓截面沿轴向施加较小的螺栓荷载，使模型完成初始接触，便于计算收敛；第二分析步施加预紧力实际值；第三分析步修改荷载施加方式为固定在当前长度。将上端板的上表面设置为耦合面，面中心点为耦合点，单角钢主材的形心轴垂直于上端板且通过其形心，进而设置第四分析步，根据图2的加载制度在上端板耦合点上施加垂直于角钢轴向的集中力，且在下端板底部设置固定边界条件。

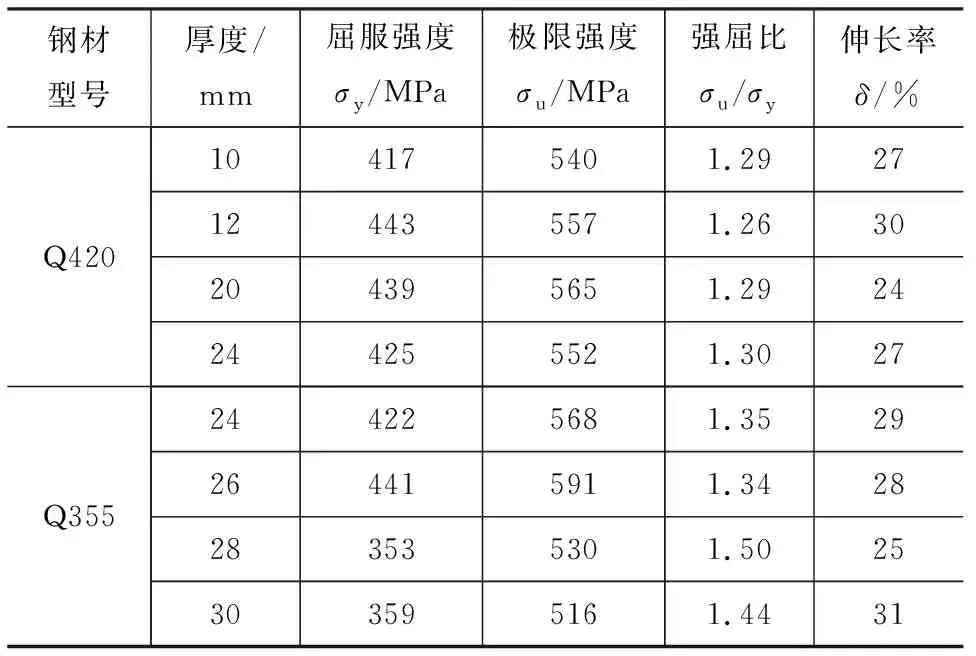
表2 材性试验结果Table 2 Results of Material Property Test

图7 过渡节点有限元模型Fig.7 Finite Element Models of Transition Joints

2.2 有限元模型验证与试验结果分析

对6个足尺过渡节点试验模型分别在受拉和受压工况下进行弹性加载试验。本节仅给出了不同加载级别下P1、H1、H2、P3四个测点的应变数据，如图8所示。可以看出，随着荷载增加，各测点记录的应变值逐渐线性增大。与其他测点相比，测点H2呈现出较大的应变值，表明水平板上对应上、下靴板的十字交汇处水平应力最大，并向四周扩散且逐渐减小。同时，由足尺试验得到的荷载-应变曲线与数值模拟吻合较好，验证了有限元模型的正确性。

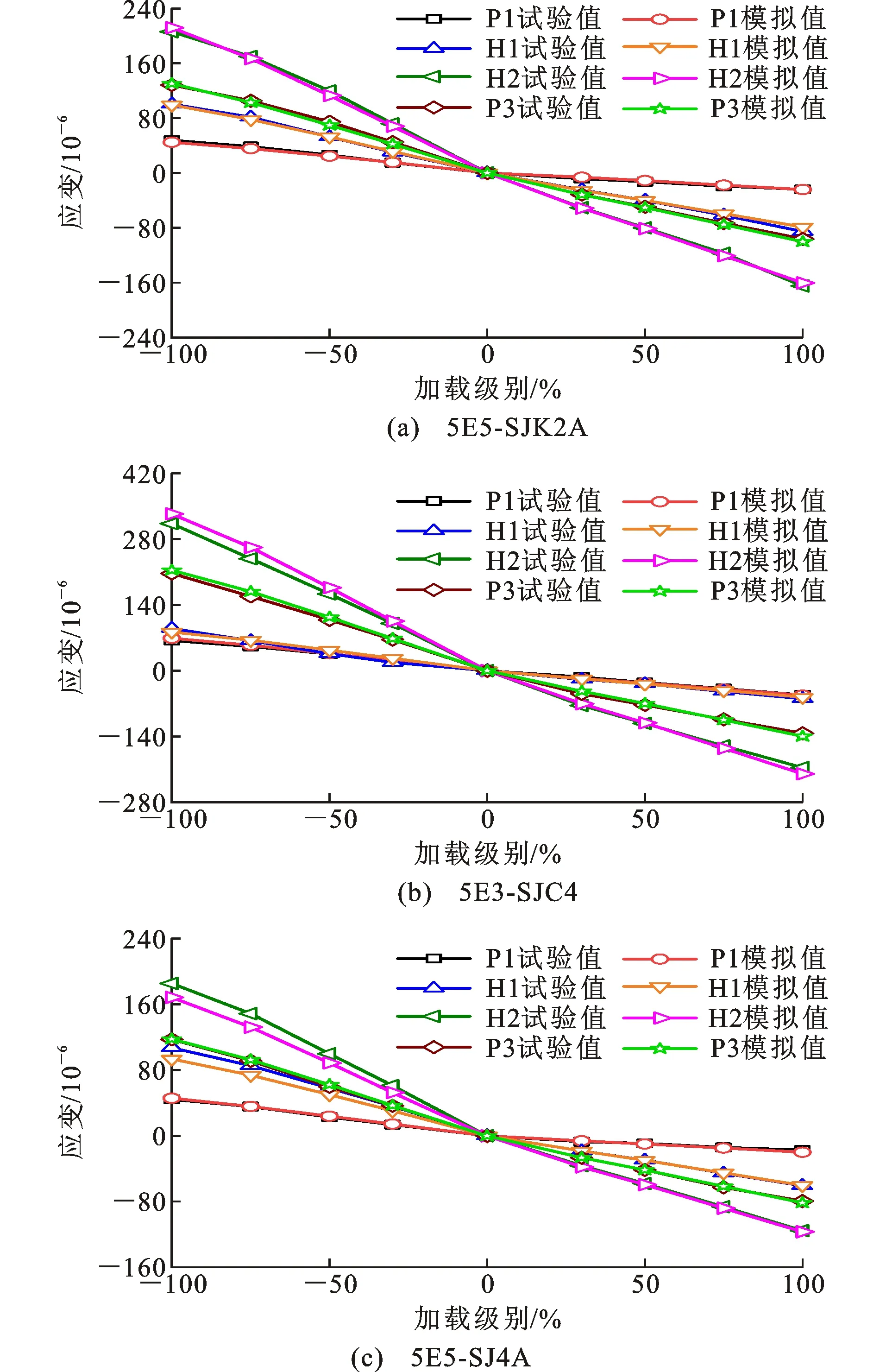
图8 弹性加载试验的应变曲线Fig.8 Strain Curves of Elastic Loading Tests

对2个缩尺过渡节点试验模型分别在受拉和受压工况下进行破坏加载试验。表3给出了不同加载级别下P1、H1、H2、P3四个测点的应变数据。通过对比加载试验和数值模拟得到的不同加载级别下各测点的应变值，验证了建立的有限元模型能够准确地预测过渡节点的受力情况。通过表3可以看出，随着荷载增加，各测点的应变逐渐线性增大。与弹性加载试验得到的应变分布规律相同，位于靴板与水平板相交区域的测点H2应变最大，表明靴板与水平板的相对位置对水平板的受力有很大的影响。

表3 破坏加载试验的应变值Table 3 Strain Values of Failure Loading Tests

当荷载达到940 kN时，过渡节点的连接板件发生明显的弯曲变形，此时终止加载试验。图9给出了破坏试验中过渡节点的变形模式，并与数值模拟进行对比。由于上、下靴板与水平板的连接焊缝存在偏心距离，当荷载传至水平板时，偏心弯矩较大而导致水平板发生弯曲变形，如图9(a)、(b)所示。发生弯曲变形的水平板通过焊缝影响了上、下靴板的受力情况，进而导致上、下靴板出现明显变形，如图9(c)、(d)所示。通过图9可以看出，由破坏试验得到的过渡节点变形模式与数值模拟吻合较好，进一步验证了有限元模型的正确性，为后续的单变双角钢过渡节点模拟分析奠定基础。

图9 试验与数值模拟变形对比Fig.9 Comparison of Deformation Between Test and Numerical Simulation

3 单变双角钢过渡节点计算方法比较

由于上、下靴板与水平板连接焊缝存在较大的偏心距离，当荷载从上靴板经过水平板传至下靴板时，在水平板上产生的偏心力矩是影响其受力的主要因素。基于单变双角钢过渡节点理论分析与数值模拟，文献[19]分析了上、下靴板与水平板连接焊缝的偏心距对水平板受力的影响规律，对水平板上的不均匀应力进行等效，通过引入弯矩调整系数和弯矩强化系数，提出了一种确定过渡节点水平板厚度t的计算方法，即

(1)

(2)

式中：α为弯矩调整系数；β为弯矩强化系数；Lh为水平板长度；Lw为水平板宽度；F为施加荷载；e为上、下靴板的偏心距；Lz为上角钢肢宽；f为水平板强度设计值。

根据不同偏心距下单变双角钢过渡节点的弯矩调整系数α散点分布规律，为了保证水平板的计算厚度满足过渡节点的受力要求，将弯矩调整系数α采用双线性模型进行包络处理，如图10所示。

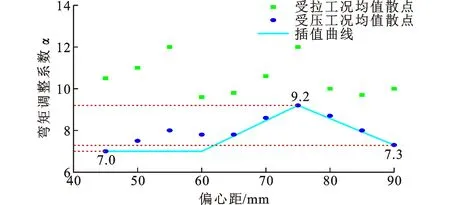
图10 偏心距与α关系Fig.10 Relationship Between Eccentricity and α

如前所述，目前关于单变双角钢过渡节点水平板厚度的规范没有给出相应的计算公式，导致在节点设计中存在较大的盲目性和主观性。为了评估文献[19]中水平板厚度计算方法的合理性，进一步对比了已提出的水平板厚度设计方法和上述试验结果。

文献[9]考虑水平板上弯矩分布的不均匀性，将弯曲应力作为水平板承载力的主要控制因素，提出了水平板弯矩比值与惯性矩的关系，推导了水平板厚度计算方法，即

(3)

式中：κ为力传递系数；Mp单位长度弯矩。

文献[20]通过分析单变双角钢过渡节点的受力机制和破坏模式，明确上、下靴板的几何交汇处出现明显的应力集中现象，提出了应力扩散长度将水平板中的不均匀应力进行等效，进而推导了水平板厚度计算方法，即

(4)

式中：α′为内力系数；L为应力传递强化长度；q为等效均布线荷载。

采用上述计算方法计算了编号5E5-SJK2A、5E3-SJC4和5E5-SJ4A的过渡节点水平板厚度，结果如表4所示。可以看出，对不同单变双角钢过渡节点采用文献[9]与文献[20]计算的水平板厚度均比设计(试验)厚度大，表明这2种设计方法偏于保守；文献[19]计算的水平板厚度均比节点设计(试验)厚度小，表明这种方法对节点水平板厚度实现了进一步优化，其中5E5-SJK2A过渡节点的厚度优化效果最好，优化率达14.1%。

表4 不同水平板厚度计算方法对比Table 4 Comparison of Calculation Methods for Different Horizontal Plate Thickness

为了验证计算方法的合理性，以编号为5E5-SJK2A-2的过渡节点为例进行数值模拟分析。该过渡节点的设计偏心距为76 mm，将表1中的尺寸参数代入公式(3)、(4)中，得到水平板计算板厚为26 mm，并与水平板设计(试验)板厚30 mm进行对比，如图11所示。可以看出：受压工况中，厚度优化前后的水平板均未达到屈服，厚度为30 mm和26 mm的水平板最大应力分别为288 MPa和325 MPa，且优化后的水平板材料利用率明显提升；受拉工况中，厚度为30 mm的水平板最大应力为278 MPa，厚度为26 mm的水平板最大应力为327 MPa，均未达到屈服，表明优化后的水平板满足过渡节点的设计要求。

图11 5E5-SJK2A过渡节点设计板厚与计算板厚的应力云图对比Fig.11 Comparison of Stress Nephogram Between Design Plate Thickness and Calculated Plate Thickness of Transition Joint 5E5-SJK2A

综上所述，文献[19]通过考虑上、下靴板偏心距对水平板受力的影响规律，明确了过渡节点的力学特性，并对水平板上的不均匀水平应力进行包络强化。通过与过渡节点设计厚度进行对比，验证了该方法不仅具有良好的水平板厚度优化效果，也能够满足水平板承载力要求。将提出的方法应用于实际工程中能够节约过渡节点的耗材成本，为过渡节点的结构设计提供指导。

4 结语

(1)通过开展单变双角钢过渡节点真型试验，研究了弹性工况和破坏工况下过渡节点的受力特性，确定了过渡节点的极限承载能力，且有限元模拟与试验结果吻合良好，验证了有限元模型的合理性。

(2)单变双角钢过渡节点真型试验和数值模拟结果表明，水平板上对应上、下靴板的十字交汇处水平应力最大，并向四周扩散且逐渐减小，明确了偏心距是影响过渡节点受力的主要因素。

(3)通过与水平板设计(试验)厚度进行对比，对现有的过渡节点水平板厚度计算方法合理性进行了评估，分析了不同计算方法的厚度优化效果和安全裕度，为单变双角钢过渡节点的结构设计提供指导。