点·线·面·体：初中数学复习教学的设计与实践

胡柳青|浙江省桐庐县分水初中教育集团

新授课由于受课时、学生学习基础、教学目标等的限制，通常采取“碎片化”的设计.这样的设计割裂知识的内在联系，忽视知识的整体建构，阻断思考的系统性.教师需要通过复习课弥补上述缺陷，将点状、零碎的知识整理成线网状、系统性的知识，澄清疑难困惑，提炼并升华教材的思想和方法.然而，数学复习教学经常存在欠系统、模式单调、学生地位缺失等问题，其以“勤讲授、快节奏、大题量、高密度”为特征，将知识总结、题型归类异化为复习的终极目标.这缘于教师不明晰数学复习的特点.以下，笔者先梳理数学复习的特点，然后从“点·线·面·体”方面提供有针对性的教学策略.

一、数学复习的特点

复习是学生对已学知识再加工，让认知结构更优化的学习过程.复习教学的主要目标在于温故然后知新，查漏进而补缺，从而完善结构、形成方法、提升能力.数学复习教学，在加深学生对数学知识的理解、促进结构的条理化与系统化方面，具有不可替代的作用.

（一）重复性

数学复习中的学习对象是教师已经传授过的、学生已经研究过的，从这个意义上来说，数学复习内容具有重复性.认知心理学表明，任何学习都包括信息的感知、加工与记忆等过程，要使个体的信息从短期记忆进入长期记忆，意义建构与复述是必不可少的.因此，在章节（或单元）中安排一定量的复习，符合学生认知发展螺旋上升的规律.

（二）概括性

数学复习是重复性的学习活动.新知学习注重数学知识的获取过程、感受知识形成的心理经历、体验技能方法的形成过程等；复习则注重对求解过程的合理性进行反思、把相关性质作为知识对象来认识等.二者对信息精细加工的层次与水平有着显著差异，复习时将过程性转化成对象性，提高了概括的层次.此外，单元学习内容中往往贯穿着数学思想，而这很难在某一课时的新知学习中体现，因此复习时需要对这些数学思想方法进行提炼，对问题解决的通性通法进行归纳，对问题解决的策略方法进行总结.

（三）系统性

数学复习通常要求学生在对象化的基础上建构本单元的知识，使其与其他单元或不同学科知识乃至现实生活，建立简约化、多触点、结构性的知识体系.学生要通过学习经验与生活经验间的联系与作用，将单元知识纳入自己的认知体系，建立知识知觉特有意象之间的联系，形成颇具个性化、系统性的认知结构，由此达到梳理与巩固知识的目的.

（四）综合性

数学复习需要完整梳理知识，形成认知结构，需要综合应用知识，提炼思想方法和解决策略.教师可通过应用知识解决实际问题，引导学生进行模式化的提炼，并用数学语义加工新知学习中内隐的程序性体验，使其外显出来，以此解决相关问题，并把经验的语义加工结果重新内隐化，提升解决问题的能力.

（五）反思性

数学复习需要引导学生回顾并梳理知识，初步形成个性化的知识体系.教师要引导学生重新认识知识体系，并在生生交流、自我和他人的评价中反思与改进知识体系.学生在应用知识解决问题时，要对解题过程进行实时评价与自我反思，以发展自己的数学思维和解决问题的能力.

二、初中数学复习教学的“点·线·面·体”

笔者对初中数学复习开展了大量的案例研究，发现利用联系的方法复习知识，将相对单一、分散、零乱的知识与方法，通过变式、引申、拓展等方式联点成线、融线成面、合面成体，可促进学生对知识与方法的再认识、再理解、再提升，使学生从更高层面、更新角度去激活知识、拓展思维、生长智慧.

（一）生成：激活“知识点”，在厘清知识点中寻找薄弱环节

数学教材重视知识学习的整体性，具有清晰的知识图式.学生“不识庐山真面目”，是“只缘身在此山中”.因此，复习教学时，教师要站在系统的角度，视章节重点内容为“点”，审视其在整个学科中的地位与作用，设计利于学生多角度联想的问题，帮助学生突破原有知识的局限，丰富对原有内容的认识，拓展原有方法的深度.所选的习题，往往要求具有代表性、易于说明问题，务必突出重难点，能够体现课程最重要的内容和最基本的要求.

【案例1】代数式复习

问题1：当x=-1时，求代数式x2-2x+3的值.

问题2：（1）若a+b=-1，求3a+3b的值；（2）若x2+2y2+5的值为7，求代数式3x2+6y2+4的值；（3）当x=2时，代数式ax3+bx的值为8，求x=-2时，代数式ax3+bx的值.

问题3：用100米长的篱笆围成一边靠墙（足够长）的长方形养殖场，设养殖场靠墙一边为x米：（1）用代数式表示养殖场的面积；（2）当x分别为5、25、35时，养殖场面积为多少？x可取60吗？（3）当x为何值时，养殖场的面积为1050平方米？（4）当x在什么范围时，养殖场的面积大于1050平方米？（5）你能猜想养殖场的最大面积为多少吗？

案例说明：用字母表示数需要具备一定的抽象思维能力，代数式求值通常涉及多种运算，是方程、函数、不等式学习的重要载体，也是学生学习的薄弱环节.问题1、2关注重点内容，明确代数式求值的步骤与注意事项，尝试运用整体思想代入求值，使学生从数的认识上升到字母的认识.问题3对所学内容进行整体回顾，使学生经由代数式，逐步进阶到由字母变化导致代数式值变化并得到函数，形成知识框架（如图1，见下页），从而有效突破学生思维的局限性.

图1 代数式与不等式、方程、函数、代数式求值的关系及代数式求值的注意事项

“点”式复习教学注重即时反馈、及时检测、随时跟进.教师在指导时应到时到位，重视学生的薄弱环节，帮助学生寻因、纠错、总结、反思.“点”式复习还强调“全覆盖”：复习内容应尽量全面，呈现所有的独立知识点；复习目标应面向所有学生，要求各层次学生均有提高.此外，教师还要注意适当延伸知识，以提升学生的思维品质和创新意识.

（二）生长：联成“知识线”，在梳理知识脉络中进行整合联系

数学教材的章节编排存在着有利于学生感悟的逻辑顺序，在某一章节的众多知识中，总有某一知识是其他知识的源头，统领着其他知识的生成.复习教学的主要任务就是建构全章的知识网络，所以不能简单、零散地再现知识，而要立足于全章的核心知识，遵循认知规律，按知识发生、发展、延伸的“线”型路径梳理、整合知识，帮助学生形成整体认知，培养系统思维.知识之间的联系越紧密，与其他知识的联系越丰富，地位也就越重要，拓展性也就越强大.“线”式复习就是要把某一知识点，遵循知识结构的纵向脉络及递进方向开展习题变换，以达成基础知识、基本技能的深入发展，使学生对重难点知识从基本掌握走向熟练掌握，从基本理解走向深刻理解.

【案例2】相似三角形复习

问题1：△ABC中，D为边AB上的一点，AD=10，DB=5，AC=12.求作点E，使E点在边AC上，使△ADE与△ABC相似.

问题2：（1）移动问题1中△ABC边AC上的点E，使其与点C重合，得到母子相似三角形，则哪些三角形是相似的，有何种线段关系？（2）若E为AC中点，CD⊥AB，延长CB至F点，连接FE，则又有哪些三角形是相似的，有何种线段关系？（3）对母子相似三角形的边进行特殊化，若AB=AC，则∠B多少时，其中两个三角形会相似？强化条件，若CD⊥AB，BE⊥AC，又有哪些三角形会相似？弱化条件，若∠BEC=∠BDC≠90°，上述结论是否仍然成立？

问题3：（1）△ABC中，增加三边中点D、E、F，你能证明△FED∽△ABC吗？（2）改变形状，若是内接正方形或长方形，你能得到什么结论？（3）叠加图形，并进行位置变化（如图2），你又能得到哪些结论？

图2 中点三角形叠加变化

问题4：（1）我们对相似图形尝试了许多变式，上述图形是否存在位似？位似与相似有什么联系和区别呢？（2）在矩形ABCD中，E、F、G在三边BC、CD、AD上，∠AEF=∠EFG=90°，AE=EF=4，FG=2，求AB、BC.（最后还可进一步变化为一线三等角）

案例说明：几何是研究“空间结构”的一门基础科学，其一是图形本身结构，强调定量研究，其二是图形变化形式，强调定性研究.以上案例利用“平行相似”和“斜交相似”基本图形，采用弱化或强化、组合或增删等方式，层层递进，环环相扣，变式得到相似三角形的几乎所有常见而有用的典型图形，并将之全景式、关联性地呈现于学生的视野之下，形成一条完整的知识线.

“线”式复习注重知识的横向拓展，强调由浅入深、从易到难.既注重习题的生长性，要求善于拓展变式，又注重习题的本质，要求善于归类总结；既可通过不同角度，采取不同模型，利用不同命题，指向相同方法、相同本质，又可从单个知识向多个知识延伸，以点带面、举一反三，明晰内涵与外延，寻找方法获取思想，由量变走向质变.如此纵横捭阖、前后连贯，学生才会深入理解知识的生成与发展，进而串起知识点，连成知识线，触类而旁通.

（三）生法：融成“知识面”，在基本问题融合中拓宽认识视角

数学教材把大量的概念、命题和基本原理整编成一个系统，是为了方便学生学习，让他们能在短短几年中学完几十个世纪才完备的知识.虽然高效，弊端却也显而易见：学生知道的只是知识间因生成而拥有的因果关系，认识较为单一，不利于后续学习.数学复习就是要打破学生对原有知识的单一认识，使他们重新组合原有内容，拉近知识间彼此割裂的关系.教师可将章节中最基本的问题视为突破口，引导学生再次探究，在全章乃至全学年（学段）教材的“面”上变换知识的原来顺序，打破内容的固有界限，改变原有的认知方式，帮助他们进一步融合知识，形成体系.由于研究方式有所变化，学生在进一步理解原有知识的过程中，一定会产生新的知识或新的问题，也就是所谓的“温故”而“知新”.“面”式复习要让学生学会发现、学会思考、学会联系、学会总结，在问题解决的过程中逐步领悟思想方法，逐渐明晰知识的横向和纵向联系，形成知识网状体系，使错综复杂的“知识线”有条不紊地形成“知识面”，从而整体把握问题，提升学习能力.

【案例3】中点四边形探究

问题1：（1）中点三角形与原三角形有什么联系？（2）若F、E、D为三等分点，△FED与原三角形又有什么联系？（3）若将三角形变为四边形，所得中点四边形与原四边形有什么联系？

问题2：（1）任意四边形的中点四边形是什么四边形？（2）若原四边形为特殊四边形，中点四边形是否为特殊四边形？你是如何思考的？（3）反向思考，若中点四边形为特殊四边形，原四边形会是什么样的四边形？（4）你能运用其他方法来说明矩形（菱形）的中点四边形是菱形（矩形）吗？（5）若将四边形对角线中点纳入研究视角（如图3），你又有什么想法？

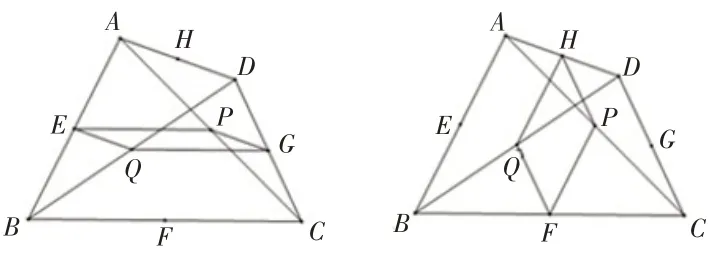
图3 四边形对角线中点变化

问题3：（1）中点多边形和原多边形的周长、面积是否存在联系？运用“几何画板”进行探索，并用恰当方式表示.（2）利用“几何画板”，拖动顶点P（如图4），可产生多种图形，你会研究些什么？想象一下，若点P运动到与△ABC不在同一平面上，你又能发现哪些有趣的结论？

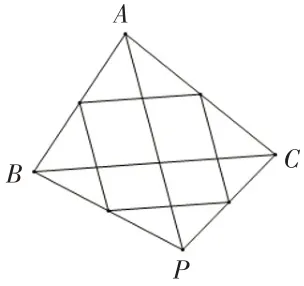
图4 “几何画板”图形变化

案例说明：对“中点四边形”进行探究，是对所学平行四边形（特殊平行四边形）的复习提升，也是三角形中位线性质的运用与巩固.案例从中点三角形的点变化与形变化中自然引申到中点四边形，然后从一般到特殊，从特殊到一般，从静止到运动，从中位线到全等（特殊）三角形再到解析几何，从二维到三维，生成新问题，获得新发现，寻到新途径，带来新思考，走向“思考—发现—研究—解决—再思考……”的研究之路，完美诠释了几何研究的一般方法（如图5）.

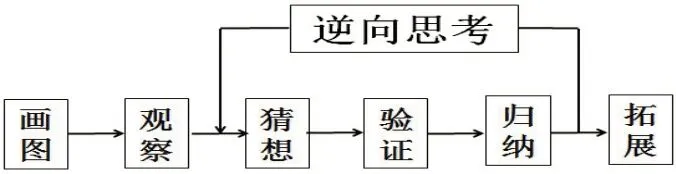
图5 几何研究的一般方法

“面”式复习不仅注重章节本身的知识，更重视知识的迁移使用，力求全景式地呈现概念、内涵和外延.通常可着眼于思想方法的某个层面进行教学，而不只是知识的简单运用.教师应重视数学理解和问题探究的互相支撑、和谐发展，强调直觉、试验、归纳、猜想等思维训练，让学生经历探索过程，获取成功体验.教师还要为学生理解、分析与解决问题提供模型和范式，归纳与概括常用的思想方法、解题策略.

（四）生慧：合成“知识体”，在项目化学习中提升核心素养

孙晓天教授认为素养不是通过灌输，而是经过教师引导、学生经历和过程体验养成的.因此，要让数学素养真正成为学生的素养，必然要改变传统的课堂教学方式.而要促使学生尝试数学思考、拓展思维空间、学会推理证明，数学学习的“生活味”“活动味”务必浓厚.学生的幸福感正是源自“丰富多彩的活动”，学生最喜欢的学习方式恰恰就是实践操作、互助交流.因此，数学复习不能只考虑知识的发生、发展、发散，更要关注形成技能方法、探究数学思考、优化问题解决、养成情感态度，直至提升核心素养.“体”式复习以课题研究、项目化学习为主要载体，学生围绕某个支点积极探索并扩散到不同领域，以此提升综合实践能力及数学核心素养.

【案例4】怎样选择较优方案

情境创设：小男孩与妈妈来缴话费，看到“移动畅打无忧”优惠活动（略），母子经过商量选择某一方案，每月100元左右话费可节省20元.

合作探究：（1）理解优惠方案；（2）明确选择原因；（3）理解话费计算；（4）建模解决问题.

学生解题：（1）组建学习小组，解读、研究优惠活动，形成方案1；（2）对具体话费计算进行探究，形成方案2；（3）建构方案1、方案2的函数解析式，画出图象，比较哪一个更优惠.

展示评价：学生展示研究成果，教师作出合理评价，并让学生进一步思考：（1）小男孩妈妈节省20元钱是选择了哪种方案？月通话时长大概是多少分钟？（2）你能将此方案的函数解析式及图象表示出来，并联系上两个方案思考应该如何选择吗？（3）你能否给移动公司提些好的建议，改进“移动畅打无忧”优惠活动，使其更加“以人为本”？

成果运用：利用周末寻找出租车阶梯收费、旅行社优惠、公司工资待遇等相关问题，用今天所学的方法完成最优方案的选择.

案例说明：“怎样选择较优方案”是一次函数简单应用之后的拓展提高.上述案例利用项目化学习进行复习，很好地诠释了“问题驱动—制订计划—探索交流—成果展示—归纳应用”的学习理念.在这个富有挑战性和趣味性的研究中，充满了学生的直觉与猜测、尝试与验证、合作与争论.如此，学生不仅能获得知识技能，而且能获得研究问题的方法和经验，获取成功的体验和克难的经历，增强学好数学、运用数学的信心.

“体”式复习重视知识的有效融合、课内外的有机联系、校内外的相互沟通，能引导学生综合运用数学知识发现问题、研究问题、解决问题、反思问题.“体”式复习是以实践活动为基础的课堂教学，学生在活动中去发现、认识、理解和发展数学.教师要给学生提供实践、思考、交流、互助的空间与时间，要关注不同层次、不同品质的学生的合作，尽可能地发现、挖掘他们的潜能，引导他们形成共同认知，提升综合实践能力，达成全面发展.

综上，运用联系的观点进行数学复习，使点动成线、线动成面、面动成体，既可提高复习效率，又能促进学生对学习兴趣的重建.复习有法，但无定法，贵在得法。不同的复习内容，相异的教学对象，必然要求不同的教法与学法.教师只有在充分理解教材、学生、教学的基础上，重视复习教学的落脚点与生长点，有效厘清局部知识与整体知识的结构体系，才能引导学生实现由显性学力到隐性学力的转变，提升数学核心素养，实现可持续发展.□◢