低雷诺数下不规则颗粒沉降阻力公式的改进和验证

雷中云，邓荣东, 2，姜克冰，库建刚, 2

(1. 福州大学紫金地质与矿业学院，福建 福州 350108； 2. 福州大学—紫金矿业集团矿产资源综合利用联合研发中心，福建 福州 350108)

0 引言

许威等[4]针对球形颗粒在供水管道中的动力学特性进行理论分析，得到球形颗粒和流体的相对速度与球形颗粒阻力系数、升力系数和力矩系数之间的关系. 库建刚等[5]设计一种单球形颗粒自由沉降法来测量颗粒在流体中的运动阻力. Faroughi等[6]使用Oldroyd-B模型研究球形颗粒的松弛和延迟时间对阻力系数的影响，并对阻力系数进行修正. Ke等[7]采用三维浸入式边界-晶格玻尔兹曼方法对椭球颗粒在流体中的阻力系数和平均努塞特数的相关性进行研究，从而建立阻力系数与平均努塞特数的关联性. 但以上研究的对象均为球形和椭球型颗粒，与真实颗粒的不规则形状不符，显然，采用以往公式计算不同形状的颗粒运动阻力是不科学的[8]. 本文通过理论分析、计算模拟和实验验证对低雷诺数下不规则颗粒的运动阻力公式进行改进，提高了颗粒运动阻力计算准确性.

1 颗粒在流体中沉降的受力分析

颗粒在流体中沉降主要受到重力(F重)、浮力(F浮)、流体阻力(F阻)、压强梯度力(F压强梯度)作用，除此之外附加质量力(F附)、马格努斯力(F马)、巴塞特力(F巴)与萨夫曼力(F萨)等作用力也对其有影响[9].流体中的颗粒运动过程非常复杂，运用拉格朗日法对颗粒在流体中的运动状态进行研究，全面考虑颗粒受到的所有力的作用效果，有以下表达式：

(1)

1.1 重力

颗粒在流体介质中由于自身的质量产生竖直向下的重力，进而沉降，所受重力与运动状态无关，不能忽略.

(2)

式中：mp为颗粒质量，kg；Vp为颗粒当量体积，m3；ρp为颗粒密度，kg·m-3；g为重力加速度，g=9.8 m·s-2.

1.2 浮力

浸在流体介质内的颗粒受到流体竖直向上托起的作用力叫作浮力. 实质是颗粒在流体中，各表面受流体压力的差(合力). 由于颗粒始终完全浸没在流体介质中，浮力一直作用在颗粒上，故不能忽略.

(3)

式中：ρf为流体密度，kg·m-3.

1.3 流体阻力[10]

颗粒相对流体介质运动所受的逆颗粒运动方向上的力称为流体阻力，在本研究过程中颗粒与流体介质始终存在相对运动，故流体阻力一直作用在颗粒上，且量级与重力相同，不能忽略.

(4)

式中：A为颗粒当量直径，mm；u为流体的运动速度，m·s-1； ζ为流体阻力系数，是与雷诺数Re有关的系数，当细小的颗粒在流体粘度较大的流体中缓慢运动且Re<1时，则有如下关系式：

(5)

式中：μ为流体动力粘度，Pas. 将式(5)代入阻力计算的公式中，则有：

(6)

1.4 压强梯度力[11]

压强梯度力事实上并非真正意义上的“力”，它是由于压强不同而产生的介质加速度. 本研究过程中颗粒相对流体的沉降速度较慢，流体介质局部压强差很小，且在选矿过程中经过碎磨的矿石，基本变成非常微小的颗粒，当量直径通常以毫米计.

(7)

式中：rp为颗粒当量半径，m. 由上式可知作用于颗粒上的压强梯度力量级十分微小，对实际颗粒沉降过程影响甚小，故可忽略该力.

1.5 附加质量力[12]

颗粒在流体介质中加速运动时，将引起周围流体做加速运动. 由于流体有惯性，表现为对颗粒有一个反作用力. 这时，推动颗粒运动的力将大于颗粒本身的惯性力，仿佛颗粒质量增加了，这部分大于颗粒本身惯性力的力叫作附加质量力.

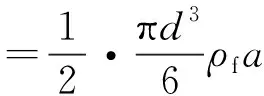
(8)

由于单个颗粒质量非常小，几乎无法带动颗粒周围流体进行运动，流体速度变化很小时，对颗粒的附加作用力难以影响颗粒沉降速度，因此可忽略该力影响.

1.6 马格努斯力[13]

颗粒在流体中围绕自身进行高速旋转时，会产生与流场的运动方向相互垂直的力，这个力称为马格努斯力.

F马=ρf(uf-up)Γ

(9)

式中：uf为流体的速度，m·s-1；up为颗粒的沉降速度，m·s-1；Γ为沿颗粒表面的速度环量.

在颗粒沉降的过程中，由于矿浆粘度大，使得颗粒在流场中自旋角速度很小，所产生的马格努斯力也很难对颗粒沉降速度起作用，因此可忽略马格努斯力的颗粒沉降的影响.

1.7 巴塞特力[14]

颗粒在粘性流体中做变速直线运动时，由于流体自身的粘性，会带动部分流体随之运动，使得颗粒受到流体运动产生的阻力，此时颗粒受到的流体作用力即为巴塞特力. 其计算式为

(10)

刘小兵等[15]认为： 在定常流场中运动时，可以忽略巴塞特力的影响. Vojir等[16]利用微积分变换的方法对不同条件下巴塞特力对颗粒运动的影响进行了数值研究，结果表明在非定常流体中，流体速度随机时，颗粒所受到的巴塞特力可以忽略不计. 而颗粒沉降过程可以看成固体颗粒在定常流体中运动，因此巴塞特力对颗粒沉降的干扰也可以忽略.

1.8 萨夫曼力[17]

颗粒在有速度梯度的粘性流体中做变速直线运动时，由于颗粒上下两端的流体速度不同，这时会产生沿着垂直方向从低速流体指向高速流体的作用力，这个力就是萨夫曼力. 当雷诺数Re<1的时，F萨的计算式为：

(11)

孙铭阳等[18]对萨夫曼力与流体阻力进行量级比较后，发现萨夫曼力也可以忽略.

2 颗粒沉降阻力公式改进

通过对颗粒在流体中受力分析可知，以往流体阻力计算仅仅考虑了雷诺数的大小、流体的粘性和颗粒大小，但并未考虑其形状，事实上，后者对阻力的影响不可忽视. 在本研究中，为方便观察、计算，同时尽量减小误差，选用粘度较大，流动性较差的流体介质，此时颗粒在其中缓慢沉降，与介质的相对运动速度较低，所受的阻力以粘性阻力为主，雷诺数Re<1，流体处于层流状态.

由式(6)可知，式中μ和dp是流体和颗粒的参数，u是与μ和dp有关的值，则μ、dp和u均无法改变.A是指颗粒与流体相对运动方向上的横截面面积，此参数会因颗粒沉降过程中发生旋转实时变化而不足以表现颗粒受力情况. 例如，对于两个形状体积完全不相同、但存在一个或数个相同横截面积大小的两个颗粒，运动到某一时刻，在相对流体运动方向的横截面积大小相等，由于两个颗粒的形状体积差异，该公式计算结果与实际颗粒所受流体阻力有较大偏差.

基于以上事实，在综合考量颗粒形状、表面积和体积的基础上，本文引入“球形度”这一系数对颗粒沉降阻力计算公式进行系数修正. 以往对于球形度的定义主要涵盖了体积球形度、直径球形度、圆比球形度、周长球形度和宽长比球形度[19]等. 在本文研究沉降阻力系数修正中，主要考虑面积和球形度的关系. 面积球形度是指物体的投影面积和最小外接圆面积的比. 颗粒形状越接近球，其球形度就越接近于1.

已知四面体颗粒的球形度为0.671，六面体颗粒的球形度为0.806，八面体颗粒的球形度为0.846，二十面体颗粒的球形度为0.939. 将颗粒球形度系数以符号k表示，值为颗粒在相对流体运动方向上的横截面面积A1与其当量直径A之比，代入颗粒在流体中的原阻力计算公式，得到在低雷诺数(Re<1)下不同形状的颗粒的阻力计算公式：

(12)

3 模拟验证

3.1 沉降模型的建立

图1 沉降过程Fig.1 Settling process

借助有限元软件COMSOL Multiphysics建立颗粒在牛顿流体中的沉降模型，采用有限元法对颗粒在流场中自由沉降的动态过程进行数值模拟，设定颗粒密度1 200 kg·m-3，当量直径5 mm，流体密度1 000kg·m-3，动力粘度0.01 Pa·s. 沉降过程如图1所示，在物理模型中将边界约束设置为滑移壁，以避免壁面对颗粒沉降的影响.

3.2 模型验证

对模拟中阻力的求解，利用COMSOL Multiphysics有限元软件的后处理功能，在模拟计算完毕后，导出颗粒在运动过程中的受力情况.

图2所绘为数值模拟和改进公式计算所得的密度1 200 kg·m-3、当量直径0.5 mm的球形颗粒，在不同流体粘度下的阻力，两者都能很好用于还原实际情况. 实验中颗粒在介质中先有一段加速运动的过程，随着速度的变大，受到的阻力不断增大，运动一段距离后受力平衡，达到沉降末速. 不仅如此，模拟和改进公式计算的结果重合度较高，表明模拟计算得到的流体阻力具有很高的可信度，因此可利用此模型改变颗粒形状，来进一步验证改进流体阻力公式的准确性.

3.3 模拟验证

本模拟设定为不同形状颗粒(密度1 200 kg·m-3,当量直径0.5 mm)在流体粘度为0.005 Pas的条件下运行，计算不同形状颗粒所受阻力，比较改进公式和未考虑球形度的原始公式计算结果的相对误差，得到图3.

由图3可知，用原始公式和改进公式计算阻力的结果与模拟计算的结果相对误差均较小，且改进公式计算值与模拟值更加接近. 二十面体(球形度0.939)在流体粘度为0.005 Pas的条件下用改进公式计算的阻力与模拟计算的阻力相对误差最小，仅为0.42%，而原始公式计算的阻力与模拟计算的阻力相对误差为0.63%. 考虑球形度计算阻力比未考虑球形度得到的值更接近模拟值，说明改进公式计算结果更为准确，且球形度越高(越趋近1)，其结果越准确.

图2 不同流体粘度下球形颗粒模拟计算与改进公式计算对比Fig.2 Comparison of spherical particle simulation calculation and improved formula calculation under different fluid viscosities

图3 改进公式与原公式误差对比Fig.3 Error comparison between the improved formula and the original formula

4 实验验证

4.1 实验材料与试剂

颗粒的沉降实验采用的流体介质为Brookfield粘度标准液，粘度μ=0.005、0.010、0.050 Pas，流体密度ρf=1 000 kg·m-3. 实验采用PμSL 3D打印技术制作的不同形状的颗粒，如图4所示，颗粒当量直径d= 0.5、1.0、3.0和5.0 mm，颗粒密度ρs=1 200和1 500 kg·m-3.

4.2 实验设备

沉降实验所用容器为有机玻璃制成的方形毛细管，高度100 mm，内边长5 mm，外边长7 mm. 使用Macro Vis Eosens型高速相机拍摄，配置XD-300-250W型冷光源. 实验配置示意图如图5所示.

图4 3D打印制作当量直径为5 mm颗粒Fig.4 3D printing produces particles with equivalent diameter of 5 mm

图5 实验装置示意图Fig.5 Schematic diagram of test device

4.3 实验方法

实验开始前将流体缓慢加入方形毛细管容器中并静置，避免产生气泡影响沉降过程. 打开相机、相机控制软件和光源； 对沉降容器的侧面进行照射； 调整高速相机的镜头中心对准光源的中心，形成拍摄平面； 校正相机，使相机成像清晰； 调整完成后相机开始拍摄，将颗粒沿管道中心线释放并使其自由沉降，记录下颗粒的沉降全过程； 通过所记录照片的数量及拍摄帧数可计算出颗粒运动时间. 根据沉降时间和距离，可得到颗粒的沉降末速.

4.4 实验结果分析4.4.1 沉降末速理论计算

图6 颗粒沉降过程中的受力分析Fig. 6 Force analysis during particle sedimentation

自由沉降的颗粒, 当重力或离心力与介质运动阻力相等时, 相对于介质的运动速度称为沉降末速. 在沉降末速计算的过程中，最简单、最基础的计算模型就是球形颗粒计算模型[12]. 因此，本文基于该模型研究，对球形颗粒的自由沉降进行受力分析. 受力分析如图6所示.

由受力分析可知：

F合=F重-F浮-F阻

(13)

可以发现，固体颗粒在流体介质中的沉降首先会有一段加速运动，随着速度变大，受到的阻力不断增大，运动一段距离后达到受力平衡，当到达动态平衡之后固体颗粒在流体中做匀速沉降运动. 可以得到沉降末速为：

(14)

4.4.2实验结果对比

将直径0.5、1.0、3.0和5.0 mm，密度1 200 kg·m-3的颗粒在流体粘度为 0.005、0.010和0.050 Pas的Brookfield粘度标准液中进行实验，计算所得沉降末速与实验所得沉降末速的相对误差共同绘制在图7.

图7 改进公式计算结果与实验结果对比Fig.7 Improved formula calculation results compared with experimental results

由图7可知，用改进公式计算出的沉降末速，与实验结果比较吻合，且球形度越高(形状越接近球体)，相对误差越小. 由图7(a)可知，颗粒当量直径越小，改进公式计算得到的沉降末速与实验得到的沉降末速相对误差越小，最小为0.41%(当量直径0.5 mm、流体粘度0.005 Pas、球形度0.939)； 图7(b)则表示流体粘度越大，改进公式计算所得沉降末速与实验得到的沉降末速相对误差越小，最小为0.17%(流体粘度0.05 Pas、当量直径0.5 mm、球形度0.939).

以上结果表明，采用改进公式能够较为准确计算出其适用范围(Re<1)内颗粒在流体中的沉降末速，且当流体粘度越大、颗粒当量直径越小、球形度越接近1时，计算结果越准确.

5 结语

1) 数值模拟结果与改进公式计算结果基本一致，且与实验结果相符，计算模型、改进公式较为准确；

3) 改进公式计算处于高粘度流体介质中的小颗粒时，相对误差较小.