利用改进初始化的残差-密集连接网络的光伏阵列故障诊断

吴文涛，陈志聪，吴丽君，程树英，林培杰

(福州大学物理与信息工程学院，微纳器件与太阳能电池研究所，福建 福州 350108)

0 引言

随着不可再生能源的过度利用，环境问题与能源枯竭等问题的相继出现[1]，人们迫切需要可再生能源. 太阳能以其清洁、环保、取之不尽用之不竭的优点从众多能源中脱颖而出[2]. 光伏发电是目前利用太阳能的主流，而光伏阵列是实现这一转换的核心器件，发展迅速. 但是光伏阵列需要长时间工作在恶劣的自然环境中，各种故障随之而生[3]. 这些故障严重地影响着光伏阵列的使用寿命，降低输出功率，更有可能引发火灾，威胁生命和财产安全. 仅仅依靠人工进行检测故障，极大地增加了成本. 如何有效地检测故障并进行分类对于降低维护成本，提高光伏阵列使用寿命具有十分重要的现实意义.

近些年来，众多国内外研究人员对光伏阵列故障诊断进行了大量研究[4]. 对地电容检测(earth capacitance measurements, ECM)[5]难以检测早期故障且对设备要求较高，红外图像检测[6]成本高昂且精度较低. 为了检测早期故障，同时降低成本，许多研究者将机器学习应用于光伏阵列故障检测[7-11]. 但是机器学习算法需要有大量的真实数据进行训练以及大量专业经验和手动提取特征，不同的光伏阵列可能有所差异，也就导致了其泛化性能较差. 为了解决手动提取特征和泛化性差的缺点，文献[12]利用卷积神经网络(convolutional neural network, CNN)对时序时间信号进行故障诊断，得到了一个高准确率的故障诊断模型. 文献[13]基于RGB图像和卷积神经网络进行光伏阵列故障检测和分类，得到了一个具有高泛化性能的模型. 同时浅层学习无法解决数据中高维、复杂等问题，而深度学习可以自动提取特征，很好地解决了这个问题. 但是深度学习需要有大量的真实数据进行训练，而光伏电站大部分运行在正常状态下，故障数据较少. 在只有小样本数据时，机器学习算法以及深度学习算法难以训练出一个具有高泛化性能、高稳定性的模型.

实际的光伏故障数据样本少，但是通过电脑仿真建立和实验室阵列相似的模型可以轻松获得大量仿真样本. 仿真数据和实测数据具有较高的相似度，但受实际运行环境的影响，仿真数据和实测数据仍有一些差距，机器学习算法和深度学习算法难以通过大量的仿真数据建立一个用于检测和诊断实际故障的模型. 针对以上问题，本研究首先提出了一种改进的初始化方法，将从仿真数据训练得到的权重代替随机初始化赋值给实际故障诊断模型. 同时，将残差连接和密集连接结合起来构造残差-密集连接网络，进一步提高分类准确率和收敛速度. 通过对比改进初始化方法、随机初始化方法以及密集连接网络和残差网络，实验结果表明，改进初始化方法优于随机初始化方法，同时提出的算法也优于另外两种算法.

1 仿真模型建立

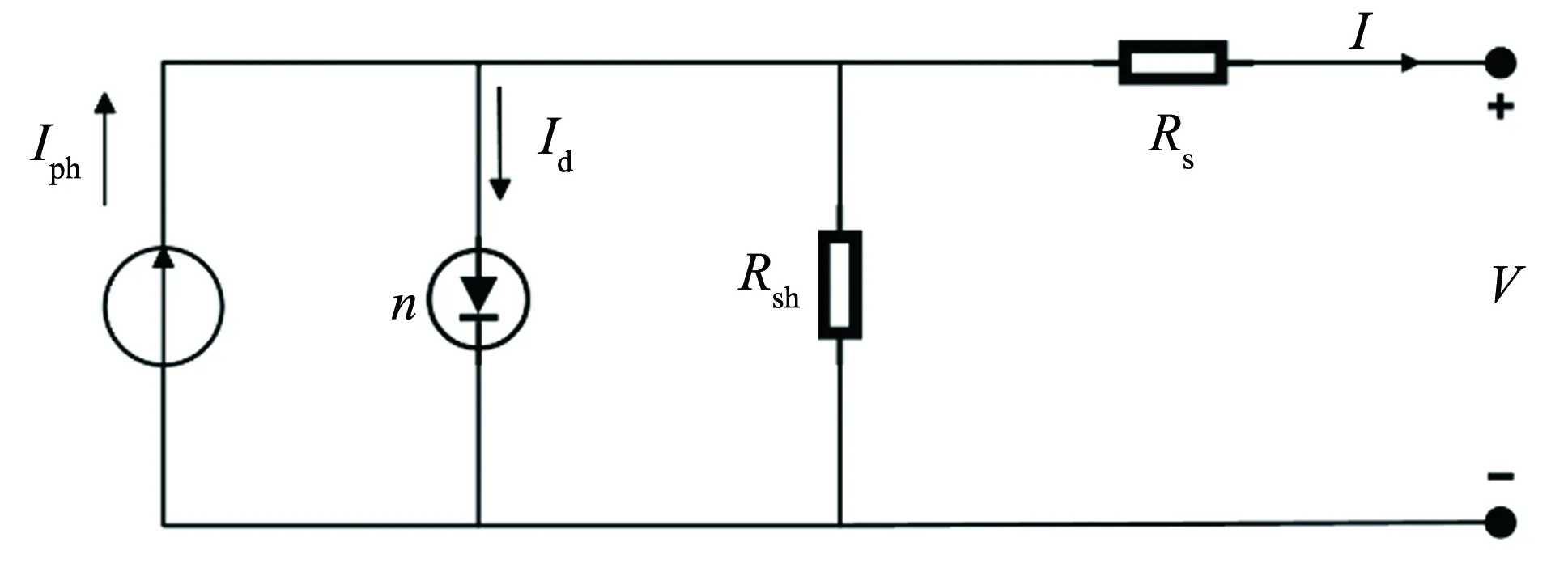
图1 单二极管模型Fig.1 Single diode model

对太阳能电池进行分析和建模，可将太阳能电池等效成为一个由光生电流源和一个二极管并联的电路，如图1所示. 图中，Rs为串联电阻，主要来源于太阳能电池中半导体材料的体电阻、电极和互联金属的电阻以及电极和半导体之间的接触电阻；Rsh为分流电阻，是由于P-N结漏电引起的.

在辐照度和温度一定时，光生电流Iph不变，可以将其看成为一个恒流源. 由图1可得到下列公式.

(1)

其中:n为二极管理想因子；Isc为饱和电流；K是玻尔兹曼常数(1.380 7×10-23J·K-1)；q是元电荷常量(1.60 22×10-19C)；T是太阳能电池工作时的温度.

当有多个太阳能电池串并联时，可将公式(1)转换为：

(2)

其中：Ns和Np分别是串联太阳能模块和并联组串的个数.

通过对光生电流，二极管理想因子, 饱和电流, 串联电阻, 分流电阻设定来建立模型. 考虑到温度以及辐照度对于太阳能电池的影响，上述公式将变化为：

(3)

其中：Isc, std是指在标准状况下(Gstd=1 000 W·m-2,Tstd=25 ℃)的短路电流；T,G分别为实测的温度和辐照度参数；α是光生电流的温度系数.

常见的故障包括开路故障、短路故障、阴影遮挡以及线路意外老化故障. 本研究光伏面板采用GL-M100的太阳能组件，将6个组件串联，后将3个串联组件并联，共计18块太阳能组件.

2 故障特性分析

辐照度为450 W·m-2，温度为26 ℃下的I-V和P-V特性分别如图2、 图3所示.从图2可见，开路故障的Isc远远小于正常状态，Voc与正常情况相比无太大变化，而短路故障的Voc比正常情况下更小，Isc与正常情况无太大变化.部分阴影对比正常情况，其I-V曲线会出现突然下降的点，随着阴影面积的变大其下降的就越严重，且从图3中可以看出阴影下光伏阵列会出现双峰.老化故障的Isc、Voc相较于正常没有太大变化，但是其最大功率在下降，填充因子下降，同时阵列老化比组件老化下降得更加严重.通过对正常及各种故障的分析，电压、电流、温度、辐照度，最大功率和填充因子特征可以将不同的故障区分出来，因此选取这6项作为输入特征.

图2 I-V特性图Fig.2 I-V characteristic diagram

图3 P-V特性图Fig.3 P-V characteristic diagram

3 光伏故障诊断方法

3.1 卷积神经网络

随着计算机视觉和目标检测的兴起，卷积神经网络(CNN)备受欢迎. 对比传统的神经网络，卷积神经网络具有如下的优势： 1) 减少参数. 由于传统的神经网络采用的是全连接的形式，要是内部神经元设置多一点就会导致计算量暴增. 但是卷积神经网络通过对上一层的感受野(卷积核在的区域则被称之为感受野)和指定大小(通常有1 ×1, 3 ×3, 5 ×5大部分是奇数)的卷积核计算得来，这就大大地减少了运算量，降低了算法的冗余度. 2) 特征共享. 在上一层输入当中某一些区域是具有相同的特征，传统神经网络没有考虑到这一点. 卷积神经网络通过卷积核将某一区域的相同特征提取出来并且共享这些特征. 其结构包括： 1) 输入层. 卷积神经网络的输入可以多种多样，可以输入一维，二维，三维的数组. 适应绝大部分的输入数据. 2) 中间层. 又叫隐含层，包括了卷积层和池化层. 卷积层是整个卷积神经网络中最为重要的部分，通常是利用一个参数可以学习的大小一定的卷积核与输入矩阵进行卷积运算，而这个卷积核会在输入矩阵上进行滑动的. 其公式如下：

yl+1(i,j)=[yl*wl+1](i,j)+bl

(4)

其中：yl+1和yl分别为第l+1层的输出和输入，也就是上文所提的特征图；b为第l+1层的偏差值； *表示卷积运算；wl+1为第l+1层的卷积核.

池化层的目的是降低参数量，通过对特征图进行压缩，降低运算参数. 采用平均池化是对卷积核大小范围内的所有参数求和，再除以卷积核大小作为新的特征. 其公式为：

(5)

其中：h,w分别为卷积核的高度和宽度；i,j为卷积核中第i行和第j列.

在卷积神经网络的最后是输出层. 通常会有1层或者多层的全连接层，将上面的特征图变为一维与这些层全连接. 最后根据任务的不同连接不同的目标函数，Softmax函数广泛地应用于多分类的任务中.

3.2 残差连接

卷积神经网络的层数对于网络的性能有着重大的影响，层数越深的网络往往有着更强大的特征提取能力. 但是网络层数的加深也带来了过拟合的问题、梯度消失和梯度爆炸现象，会导致网络模型训练速度慢，在训练集准确率高于测试集等问题. 何凯明等[14]提出残差网络(res net, RN), 通过残差连接解决梯度消失和梯度爆炸的问题，同时具有降低过拟合，训练速度快等优点. 残差结构，其表达式为：

F(X)=F(X)+X

(6)

其中：X是输入特征图；F(X)表示经过卷积运算后的输出特征图.

通过残差连接将输入和输出连接起来，可以直接学到上一层的特征而减低过拟合的影响. 同时可有效抑制梯度消失和梯度爆炸. 残差连接的思想被引入到深度学习中，大大地提高了模型的训练效率和泛化性能，使网络层数可以近一步加深.

3.3 密集连接

图4 密集连接结构Fig.4 Dense connection structure

由于残差连接可能会导致网络信息不流通的缺点，Huang等[15]提出密集卷积神经网络(dense net, DN), 通过密集连接的方式将每一个卷积层都和其他卷积层进行连接，使不同层之间的网络信息更加流通. 密集连接结构如图4所示.

与残差连接直接让两个特征图相加不同，密集连接网络是通过将特征图进行堆叠作为下一层的输入，其公式为：

Yk=Lk(X0, …,Xk-2,Xk-1)

(7)

其中：k表示网络的第k层，一般采用k=4或5；Lk表示第k层的卷积运算；Yk表示第k层的输出； (*)表示将内部所有参数进行堆叠.

3.4 残差-密集连接网络

密集连接可以改善残差网络带来的信息不流通的问题，但可能未能学习到残差连接的信息. 因此，提出一种改进方法结合密集连接和残差连接，既有密集连接的信息流通又有残差连接的信息. 且采用堆叠一次的密集连接，即k=2，这样做不仅大大地减少了计算参数，提高了运算速度，也避免了过度堆叠造成的特征冗余的问题. 其结构如图5所示. 先通过残差连接将输入和输出相加而后在通过密集连接将输入和残差连接后的特征图堆叠作为输出，兼具有残差连接和密集连接的优点.

图5 残差-密集连接结构Fig.5 Residual dense connection structure

3.5 改进初始化

图6 改进初始化方法Fig.6 Improved initialization method

随机初始化是深度学习中常用的初始化方法，通过对网络模型随机赋予初始值而后通过反向传播的方法来进行训练和调整初始值. 但是初始化对于深度学习十分重要，同一个网络模型在不同的初始值下可能会跑出一个很好的拟合而另一个可能会完全不会拟合的情况，因此初始化方式对深度学习的模型具有十分重要的作用. 在实际过程中，光伏阵列大部分运行在正常状态而故障数据较少，难以通过大样本训练来获得高泛化性能的模型. 而通过电脑仿真则可以获得大量数据，先用仿真数据训练网络模型，由于仿真数据样本大可以获得一个具有高泛化性能的网络模型，而后将该权重赋给实测数据的模型, 如图6所示. 通过这样的方法进行初始化不仅改善了随机初始化所导致的同一模型得出不同结果的情况，也可以通过小样本训练得到一个高泛化性能的模型，具有实际应用的价值.

4 实验设计与结果分析

4.1 实验设计

光伏阵列的日常发电过程中，容易出现短路故障、开路故障、阴影状况以及老化故障. 其中短路故障是光伏阵列两个点出现意外的短路. 开路故障是由于光伏阵列出现意外断路使得原来连接的线路断开，降低了输出功率，阴影状况可能是由于飞鸟的羽毛和树木的遮挡等造成光伏面板辐照度不一致的问题，降低了光伏阵列的输出功率同时也可能造成热斑损害太阳能面板，老化故障是由于线路意外暴露而造成的，提高了功率损耗. 本研究重点为设计短路故障、开路故障、阴影状况以及老化故障，因为传统方法难以在早期检测出这些故障. 创建的具体故障包括： 短路1块太阳能模块； 开路一个组串； 组串老化4 Ω和阵列老化4 Ω； 阴影故障，阴影组件的数量为1块，2块和3块.

4.2 实验结果分析

通过Simulink建模仿真获得仿真数据. 实验选择在晴天进行，对光伏阵列进行I-V曲线扫描获得实测数据，并将所得的数据分为训练集和测试集，其分布如表1所示.

训练集共有140个训练样本，测试集共有2 513个样本，通过小样本训练来模拟实际情况中数据难以获得的情况. 其训练准确率如图7所示. 3种网络对比只有网络结构不一样，其他的数据预处理、数据分布、训练步骤等参数均一致，保证控制变量. 随机初始化的网络结构为残差-密集连接网络. 可以从图7中明显看出，改进初始化在训练集收敛速度和训练稳定性高于随机初始化. 这说明改进初始化的方法具有收敛速度快，高泛化性能的优点. 而3种网络结构在训练集上无明显的差异.

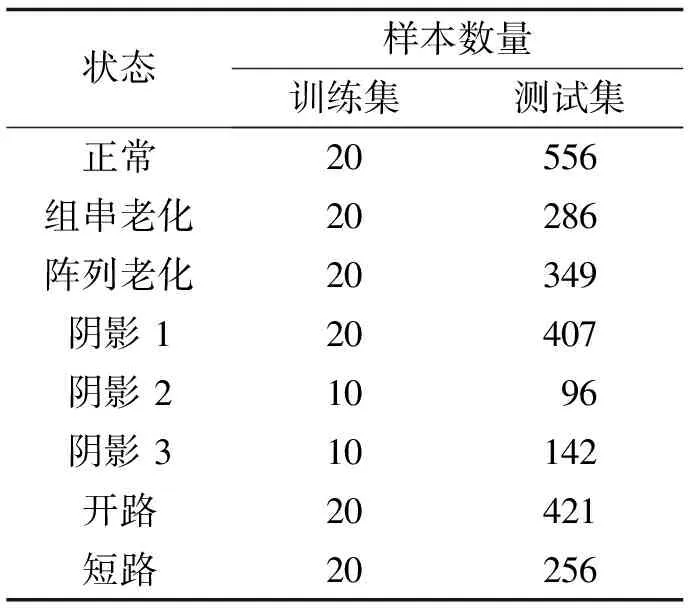
表1 数据分布表

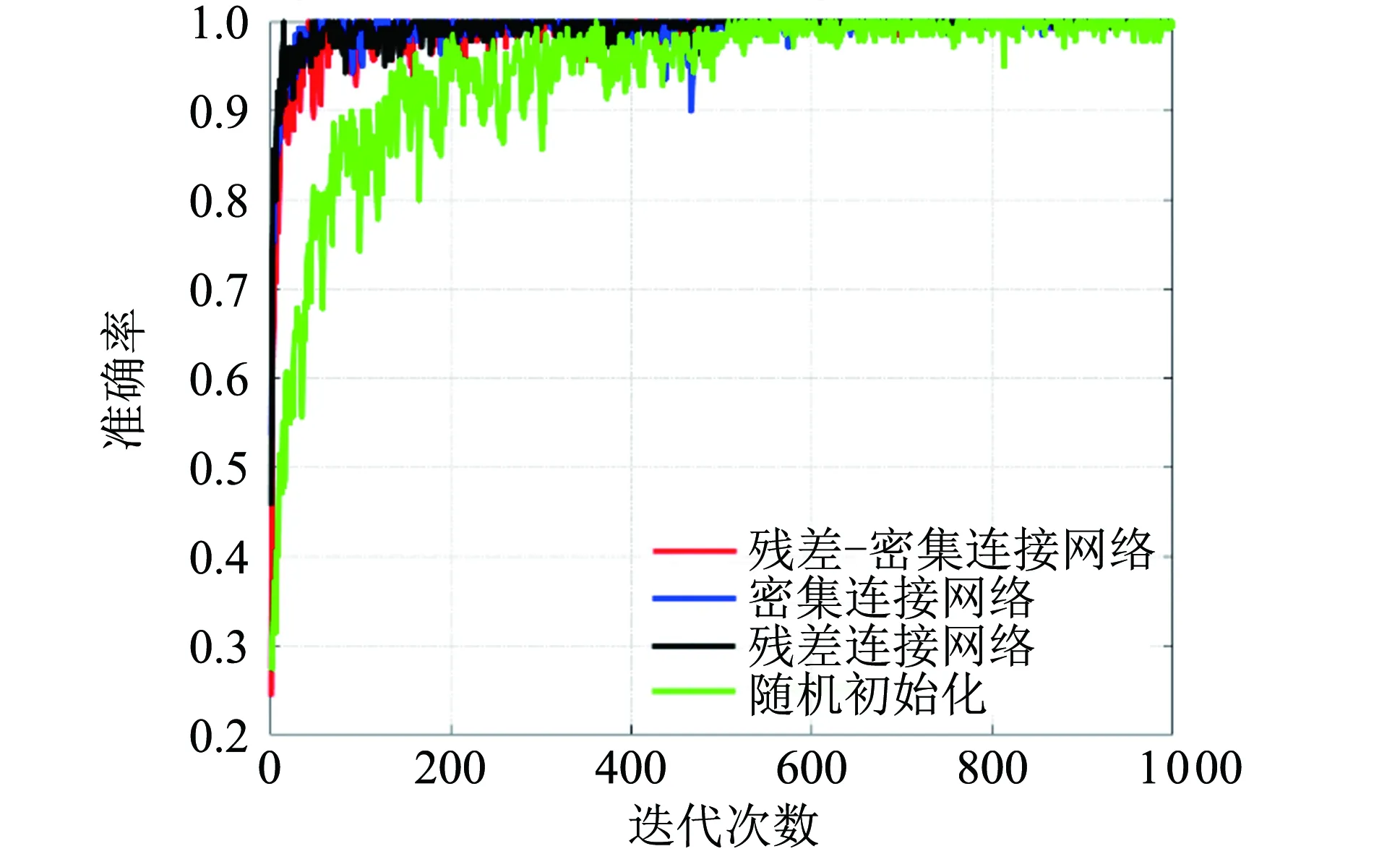
图7 实测数据训练集准确率Fig.7 Accuracy of training set of measured data

表2是重复实验的统计表，对于残差-密集连接网络，密集连接网络和残差网络是通过对仿真数据预训练5次建立5个模型而后每个模型独立重复实验10次以验证每个模型的性能. 随机初始化则是训练50次.

表2 5次预训练10次独立重复实验统计表

从表2可见，随机初始化的测试集准确率最高为95.86%而最低准确率只有70.55%，这就验证了之前的说法. 即同一个模型，随机初始化可以得到一个较好的模型，也有可能得到一个差的模型，其稳定性和泛化性能较差. 改进的初始化方法其性能要优于随机初始化方法. 同时，对比3种不同的网络结构可以发现，残差网络最低准确率为81.22%. 这就说明残差连接有时会导致信息不流通而使得模型性能下降. 密集连接网络平均准确率高达98.26%，准确率最低也有96.58%. 就说明相对于残差网络，密集连接网络信息更加流通. 残差-密集连接网络在测试时各方面的表现均为最优，说明其结构信息流通高于残差网络，也比密集连接网络多学习到残差信息，进一步说明残差-密集连接具有高稳定性和高泛化性能.

5 结语

提出一种利用改进初始化的残差-密集连接网络设计光伏阵列故障诊断的方法. 首先，对光伏阵列故障数据进行特征提取，择优选取输入特征. 其次，通过不同方法多次实验仿真采集的数据求取平均准确率来验证所提方法的性能. 其中，本改进初始化网络的平均准确率为98.63%，高于随机初始化网络的89.33%，残差网络的95.53%和密集连接网络的98.26%，证明本改进网络是具有高泛化性能、高准确性的网络结构.