基于多智能体强化学习的轨道追逃博弈方法

许旭升，党朝辉，宋 斌，袁秋帆，肖余之

（1.上海宇航系统工程研究所，上海 201109；2.西北工业大学 航天学院，陕西 西安 710109）

0 引言

近年来，随着空间领域科学技术的迅猛发展，越来越多的国家开始发射自己的卫星。虽然宇航科学造福的范围越来越大，但是太空中存在的太空垃圾和失效航天器也越来越多。这些失效航天器大多以第一宇宙速度继续在轨。若在轨航天器与这些失效航天器的轨道相交或者重合时，来不及躲避将会产生猛烈的撞击，严重威胁到一些高价值卫星和重要空间资源。于是，针对失效航天器的“在轨服务”也开始逐渐在一些航天国家得到重视。美国等国家已经开展了针对非合作目标的在轨服务的研究，并进行了一系列实验。

在非合作目标的在轨服务研究中，有一类较为重要的问题就是具有机动能力的非合作目标的交会问题。由于非合作目标的机动能力未知，而太空中航天器燃料有限，所以将此类问题可以转换为航天器的追逃博弈问题，逃逸者即为失效航天器，追捕者则为在轨服务卫星。在这类问题中考虑到多个卫星协同工作，共同实施对非合作目标的捕获，因此成为多对一轨道追逃博弈问题。

针对卫星追逃博弈问题，国内外学者已经进行了深入而广泛的研究。目前主要以微分对策求解的方法为主。文献［6］通过将追逃博弈问题转换为高维时变非线性两点边值问题，再进行数值求解的方式得到追逃策略。文献［7］利用半直接配点法对微分对策博弈过程进行求解，得到相应的数值解。文献［8］利用最优控制方法，通过求解微分对策的鞍点得到追逃博弈策略。集群追逃博弈问题中，仅知自身状态和非合作目标有限状态，未知非合作目标的未来机动信息和行为策略，且在集群卫星之间也难以形成完全状态的交流，利用微分博弈的数值方法求解比较复杂。

近年来，随着深度强化学习的兴起，有些学者找到了另外一种解决博弈问题的途径，即利用深度学习的方法对环境进行建模，然后不断训练策略，直至奖励值达到最优，完成最优博弈策略的求解。以深度强化学习为主的智能算法开始逐渐应用于求解这类复杂问题的过程中，文献［10］通过构建模糊推理模型，将多组并行神经网络的分支深度强化学习架构引入到非合作目标追逃博弈策略求解的过程中。文献［11］利用深度Q网络（Deep Q-Networks，DQN）和最大最小（MiniMax）算法求取了近距空战中的最优机动策略。文献［12］将平均场理论与多智能体强化学习算法（Multi-Agent Reinforcement Learning，MARL）相结合，对无人机集群进行了细粒度任务规划。符小卫等利用改进的分布式多智能体深度确定性策略梯度算法（Multi-intelligent Deep Deterministic Policy Gradient，MADDPG），验证了在多无人机协同对抗快速目标的追逃博弈问题中的协同围捕效果。深度学习由于其强大的拟合能力，被广泛应用于各类追逃博弈问题中。本文将利用MADDPG 算法，对追逃博弈问题展开研究。

1 问题描述与建模

1.1 多对一卫星追逃博弈问题

假设有这样一类场景，集群卫星编队在正常运行，在相对轨道上有一个非合作目标，该目标对编队卫星构成了严重的威胁，需要集群卫星协同与该非合作目标进行博弈，最终将其抓捕。而这个过程中就涉及一类博弈问题，即集群卫星追逃博弈问题。传统的方法通常是考虑博弈过程中的时间或燃料消耗，将其转换为非合作目标的最优交会问题，或者是利用微分博弈的方法，在假设对方策略是理性的前提下进行自身最优博弈策略的求解。

本文研究的多对一卫星追逃博弈是个动态的过程，博弈参与者被定义为追捕卫星和逃逸卫星，博弈双方具有相反的博弈目标，即追捕卫星需要尽力追击和捕获逃逸卫星，而逃逸卫星则需要尽可能地避开和远离追捕卫星。而在这个过程中，涉及卫星的许多真实约束，比如追捕卫星之间需要协同好策略，避免相撞，优化相互之间的策略，使得燃料消耗等指标实现最优。多对一卫星博弈场景如图1所示。

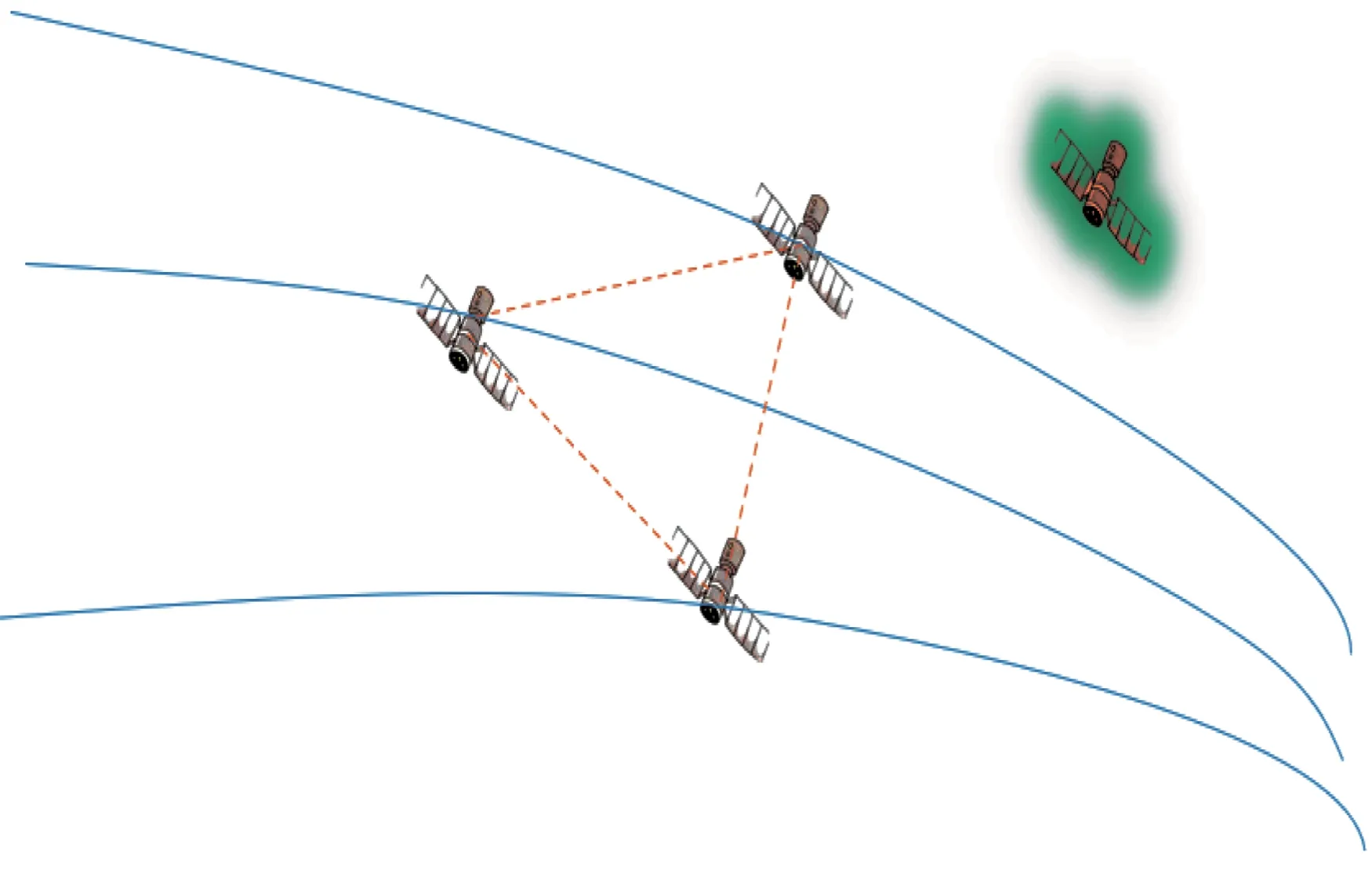
图1 多对一卫星追逃博弈场景Fig.1 Many-to-one satellite pursuit-evasion game scenario

图1 中，P(=1，2，…，)为追捕卫星。为方便距离和速度的确定，假设有一个虚拟卫星，此卫星的轨道根数为在博弈开始前的追捕卫星的平均轨道根数。在此卫星的相对轨道坐标系下，追捕卫星和逃逸卫星之间进行博弈，转换为数学模型如图2 所示。

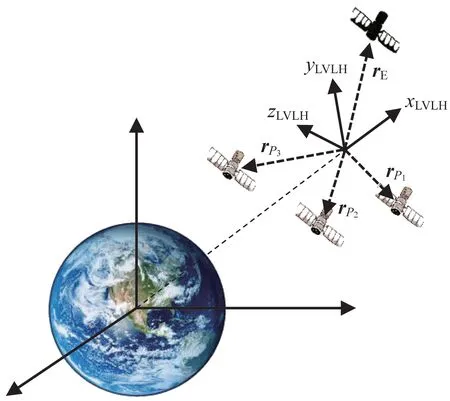
图2 博弈场景轨道坐标系Fig.2 Orbital coordinate system of the pursuit-evasion game scenario

在图2的轨道坐标系下，为逃逸卫星的位置，r，r，…，r为个追捕卫星的位 置，为逃 逸卫星的速度，v，v，…，v为个追捕卫星的速度。本文针对以上多星追逃博弈问题，构造出了集群卫星追逃博弈数学模型。

在本文研究的追逃博弈问题中，追捕卫星需优化策略去追击和捕获逃逸卫星，而逃逸卫星则也需要不断优化策略去避开和远离追捕卫星，双方的博弈构成了零和微分博弈问题。但是，在追捕卫星之间需要协调和配合完成一定的博弈目的，每个追捕卫星又相当于一个合作博弈问题，通过对博弈模型建模，利用数学模型对双方的博弈策略进行表示。双方的博弈策略数学模型如下：

式中：、J为参与博弈的卫星的机动策略代价函数。

参与博弈的逃逸卫星和每一个追捕卫星都根据代价函数优化自己的策略，目的是使得自己对应的代价函数最小。由于每一个博弈参与者的博弈策略都会影响到最后的博弈结果，而在博弈过程中博弈双方必然需要优化自己的策略到达最优。因此在进行博弈时，假设双方为理性，最终策略将形成纳什均衡条件，即：若在博弈过程中有一方策略不是最优，则另一方博弈成功的概率将会增大。这个过程数学描述为

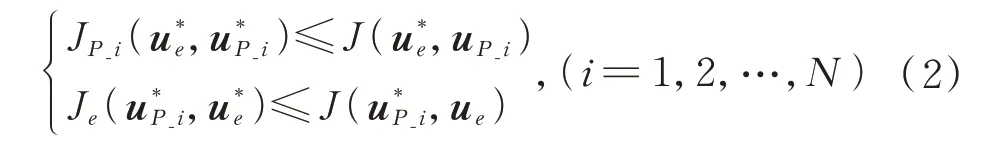
在式（2）中，当一方的卫星采用了纳什均衡策略下的动作，而对方为非理性策略，即采用纳什均衡策略以外的动作，都将使得对方的目标函数无法取得最优。

因此，在卫星追逃博弈模型中，通过求解以上最优化问题得到纳什均衡策略，从而实现追逃博弈的最优机动。

1.2 卫星动力学建模

在空间多卫星追逃博弈过程中，忽略摄动因素，卫星满足基本的二体轨道动力学。在轨道坐标系下，假设博弈开始前追捕卫星围绕着一颗虚拟参考星运行，而与非合作目标的相对距离远远小于参考星轨道运行半径，由于卫星在相对轨道坐标系下运动，所以其动力学模型忽略3阶以上小量，可描述为

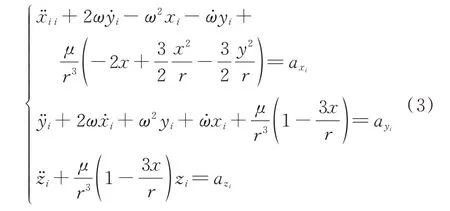
卫星的机动加速度约束公式如下：

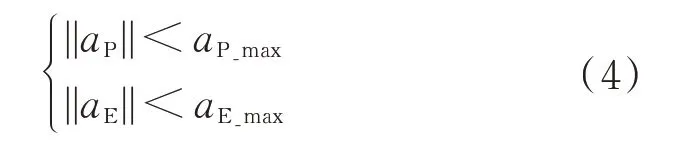
式中：、为追捕卫星和逃逸卫星的机动加速度；、为机动能力约束。

通常情况下，根据博弈的平衡性考虑，当参加博弈的双方数量有差异时，需要在机动能力上平衡，即当＞时，＜。

由于本文假定整个追逃博弈过程均在可观测的参考系轨道下，因此，规定追捕卫星和逃逸卫星的博弈机动范围为

同时，对博弈结果也进行相应的定义，由于在追逃博弈问题中，双方的博弈目的是追捕和逃逸，考虑到卫星间交会时速度与位置必须同时一致，否则将会进行碰撞产生损坏，因此，定义博弈中追捕成功的条件为

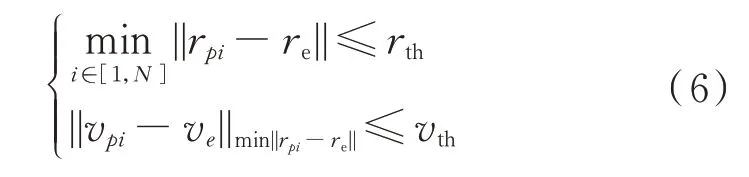
式中：第1 部分为追捕卫星中的某一颗卫星与逃逸卫星之间的距离小于等于一定的距离阈值；第2部分为当其中一颗卫星与逃逸卫星距离最近时，相对速度也小于等于一定的速度阈值。当两部分同时满足时，则定义为追捕博弈行为成功；否则，则为逃逸博弈行为成功。

2 MADDPG 算法

2.1 强化学习算法

在本文的多对一卫星追逃博弈模型中，将每个卫星看作为一个智能体，利用强化学习的方法优化策略，最终追捕卫星和逃逸卫星各自得到其最优策略，达到纳什均衡状态。

在强化学习模型中，智能体通常通过“感知信息—执行动作—获得奖励”的方式与环境进行交互，在这个不断迭代的过程中进行策略的优化学习和训练。首先，智能体通过接受环境的信号输入即环境状态；之后根据状态利用自身的策略转化输出动作a，该动作与环境交互，产生奖励r，智能体接受该奖励并根据奖励的值进行调整自身的策略，以获得的奖励值最大为目标，不断进行迭代；最终优化得到自身对于环境最优的策略。

MARL 是一类基于马尔可夫决策过程的随机博弈算法，本质过程与单智能体强化学习算法一样，都是通过不断地感知信息、输出动作，获得奖励反馈，不断迭代优化的过程，但是MARL 中由于多个智能体共同作用于环境，因此利用马尔可夫博弈描述如下：

式中：为追捕智能体；为逃逸智能体；为模型的环境状态空间；{U}为智能体的动作空间；：××→[0，1]为状态转移概率分布；{ρ}：××→R，∈为奖励函数；为奖励衰减系数。

多智能体算法可以由不同任务进行设计，比如完全合作、不完全合作、合作对抗等。本文模型中假设追捕卫星和逃逸卫星均为智能体，双方都参与策略的优化，追捕卫星之间为完全合作，与逃逸卫星之间为对抗关系。

2.2 MADDPG 算法原理

由于在多智能强化学习算法中，每个智能体在训练学习策略的时候，其他智能体的动作未知，将导致环境非平稳，因此，当智能体数量变多时策略往往难以收敛。MADDPG 是一种在多智能体强化学习领域十分受欢迎的算法，各个智能体采用DDPG 的结构，同时利用一个全局的“演员-评论家”（Actor-Critic）架构，使得各个智能体利用“集中训练，分散执行”的方法，寻找到最优的联合策略。通过这种方式，充分考虑到每个智能体的策略，集中训练时作为整体进行优化，在执行的时候各个智能体仅仅利用观测到的信息进行预测，解决了环境不平稳的问题。

MADDPG 算法的核心是“集中训练”的“演员-评论家”结构，考虑有个智能体，每个智能体对应有自己的决策网络，这个决策网络的输出就是对应智能体的策略输出。在进行集中训练时，各个智能体利用观测信息通过决策网络后进行策略输出对应的动作(π)，同时每个智能体利用一个能够接收全局信息的评价网络，对智能体决策网络的输出进行评估，得到每一个智能体输出动作对应的值函数Q。智能体的决策网络接收该评价信号，进行自身策略π的调整和优化。通过这种方式，每一个智能体的Actor 网络虽然接收局部观测信息输出动作，但是在全局的评价网络评价校正下，每一个智能体的策略都是将其他智能体考虑在内的全局最优策略。因此，在训练完毕最后执行的时候，智能体仅仅通过局部观测信息，而不需要其他智能体的策略就能够输出考虑到全局的策略动作，以此达到了分散执行时整体最优的效果。MADDPG 算法原理如图3 所示。

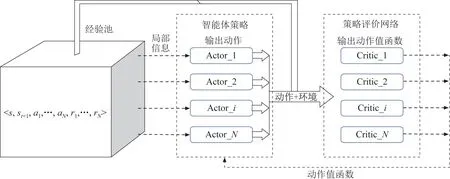
图3 MADDPG 算法原理图Fig.3 Schematic diagram of the MADDPG algorithm

MADDPG作为一种“演员-评论家”（Actor-Critic）结构的MARL，在训练优化参数时，主要有2 部分组成，一部分是全局Critic 网络的更新，另一部分是各个智能体决策网络参数的优化更新。MADDPG 在训练的时候，每一条经验池中的样本数据包括＜，s，，…，a，，…，r＞，即当前全局状态、动作后全局的状态、各智能体的动作与相应的奖励。

评价网络输入为全局信息的观测，输出为各智能体输出动作的评估，值的计算可以表示为=(s，，…，a，θ)，利用奖励值对评价网络进行更新如下：

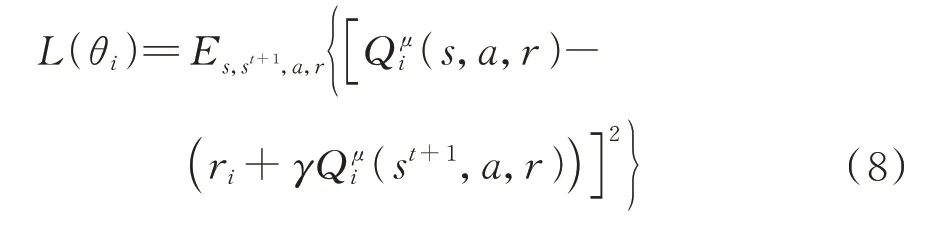
动作值函数利用当前时刻估值和动作后奖励校正后估值的均方差的方式进行更新，相当于全局的中心评价网络，有效地解决了环境不平稳的问题。

每个智能体拥有一个接收环境中状态信息输出动作的策略网络，在进行训练时，根据评价网络输出的动作值函数得到累积期望收益的梯度进行策略参数的更新。考虑到整体博弈策略是由个智能体的参数={，，…，θ}形成的策略={，，…，π}组成的，在进行集中训练时，根据贝尔曼方程在随机策略下，每个智能体的累积期望收益(θ)及其梯度∇ J(θ)为

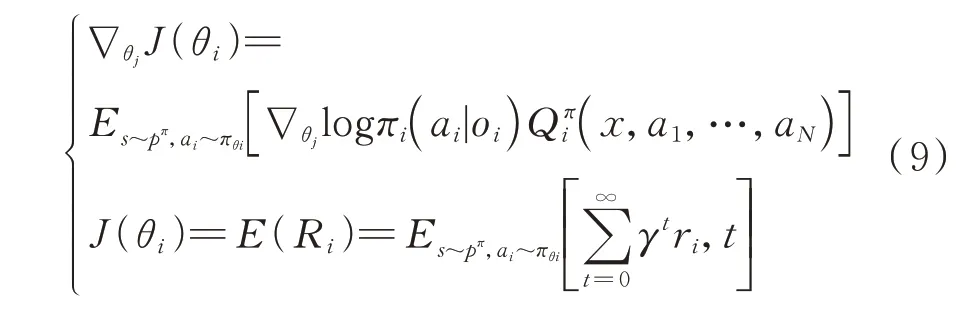
由于采用MADDPG 的确定性策略梯度，因此其更新的策略梯度如下：

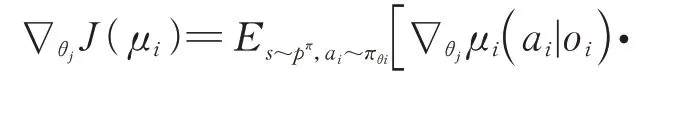
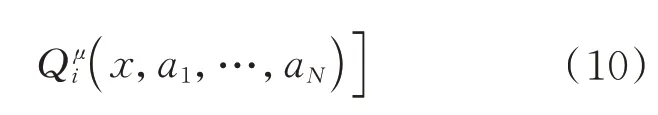
通过上述更新过程，在训练过程中决策网络和评价网络同时更新，抽取经验池中的数据。当然在算法设计过程中，双网络参数差分更新等方法不再赘述，最终完成网络的更新。

3 基于MADDPG的空间轨道追逃博弈实现

在轨道追逃博弈过程中，为使得博弈策略完整真实，追捕卫星和逃逸卫星均可看作为智能体，共同在环境中进行追逃博弈训练，最终优化得到的策略将能够充分考虑到对方的策略和机动输出，实现最优的博弈目的。本文基于多智能体深度确定性策略梯度的方法，利用决策-评价网络结构得到最优多个追捕卫星的协同策略，同时，逃逸卫星也在训练中博弈迭代，实现最优逃逸策略的求解。而每一个智能体按照相应的指标将优化得到其最优的策略，相互之间达到了纳什均衡。

最后在实施抓捕目标卫星时，只要目标卫星的机动方法不是最优的策略，将得到更好的博弈效果。

追逃博弈算法整体方案如图4 所示。为达到博弈目的，训练前需要对每个智能体进行奖励塑造（Reward Shaping）。根据博弈目的和方法的区别，分为追捕卫星博弈奖励函数和逃逸卫星博弈奖励函数。

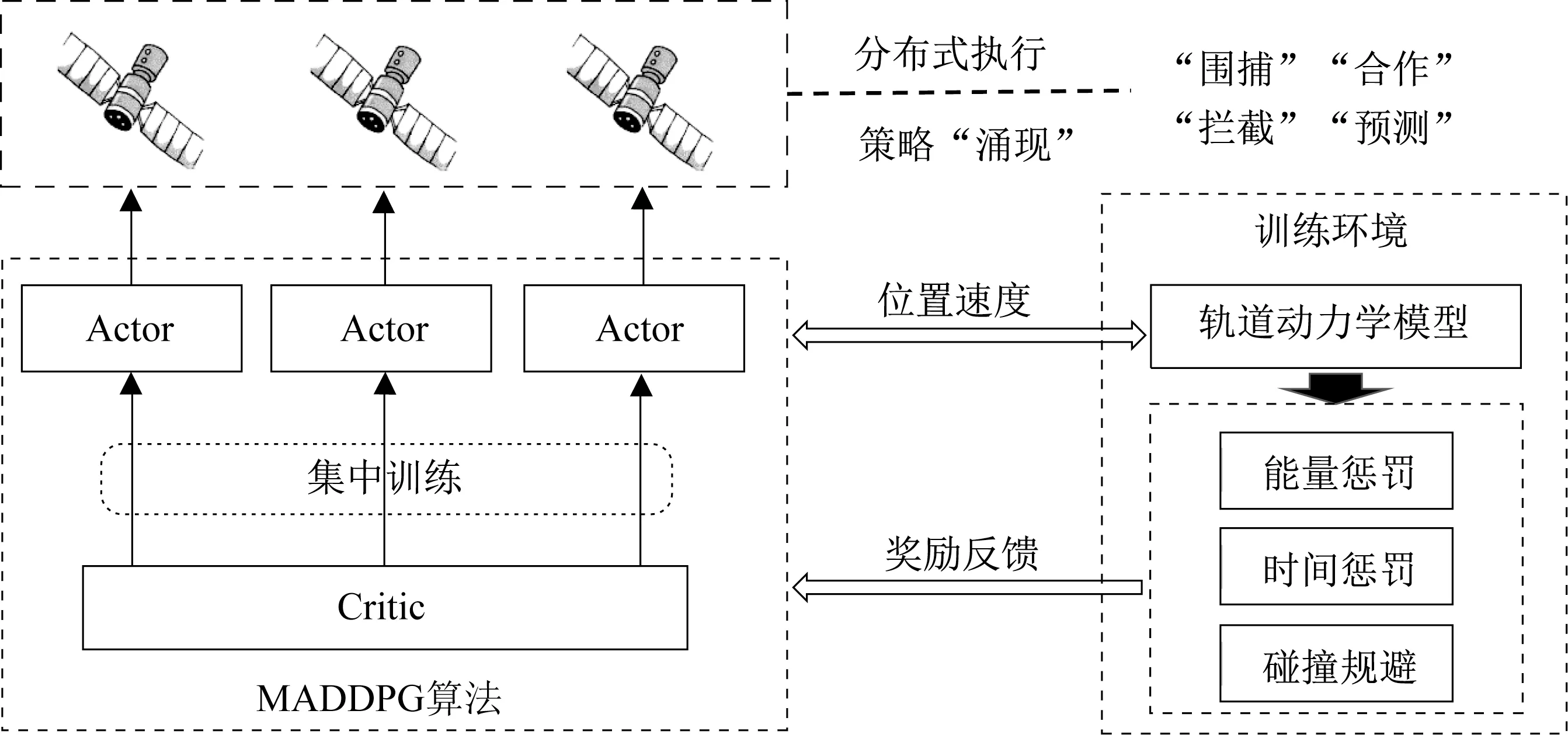
图4 轨道追逃博弈方法实现原理Fig.4 Method of the orbital pursuit-evasion game method

首先是追捕卫星捕获成功时的奖励函数设计，规定捕获的成功条件为

式中：第1 部分为追捕卫星中的某一颗卫星与逃逸卫星之间的距离小于等于一定的距离阈值；第2部分为当其中一颗卫星与逃逸卫星距离最近时，相对速度也小于等于一定的速度阈值，当两部分同时满足时，则定义为追捕博弈行为成功。

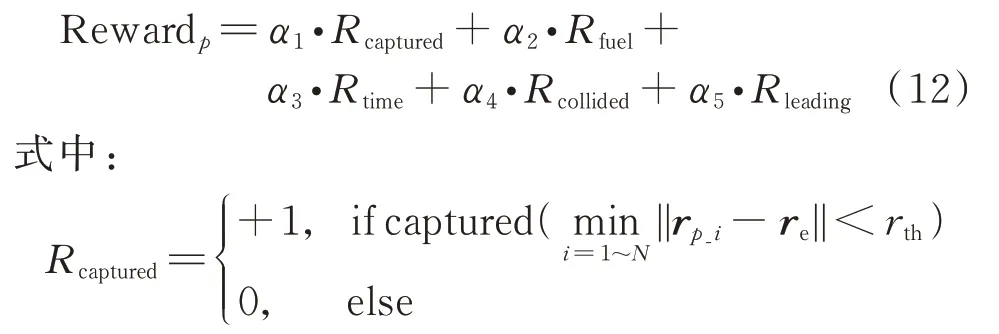
为当有其中一个卫星捕获逃逸卫星时获得任务正向奖励；=-||Δ||为对卫星在追捕过程中燃料消耗的惩罚，为了防止追捕时间过长，在奖励函数中加入了＜0，将时间作为惩罚，让追捕卫星能够以更快的速度捕获到逃逸卫星，考虑到集群卫星在追捕过程中要避免碰撞；

为当集群卫星中相互碰撞后进行负奖励作为惩罚；同时，由于稀疏奖励可能产生不容易收敛的问题，利用强化学习奖励塑造的方法，在博弈过程中增加引导性奖励；

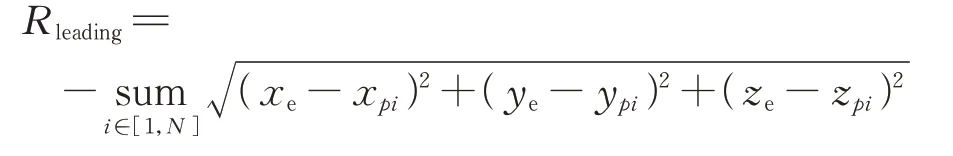
为多个智能体卫星与逃逸卫星的整体距离越小，则奖励越大；、、、、为各奖励的权重系数，可根据具体任务调整大小。

逃逸卫星的目的是能够最大限度地避免被追捕卫星捕获，因此在环境交互训练中，逃逸卫星每一步的奖励函数设计如下：

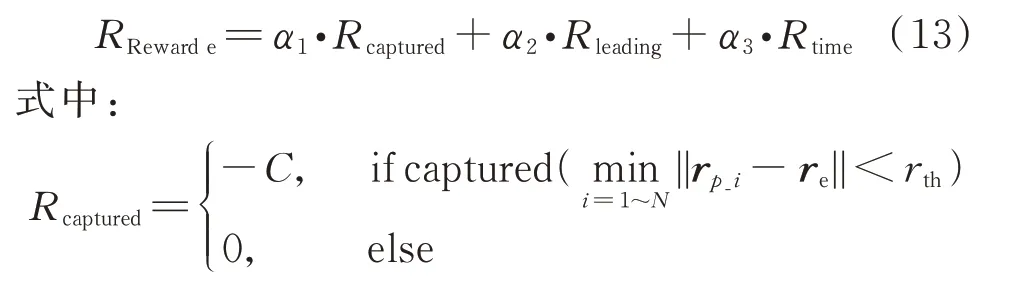
为被捕获后的惩罚；由于只通过目标奖励容易造成稀疏奖励无法收敛，因此根据强化学习奖励塑造中目标一致的原则，加入引导奖励

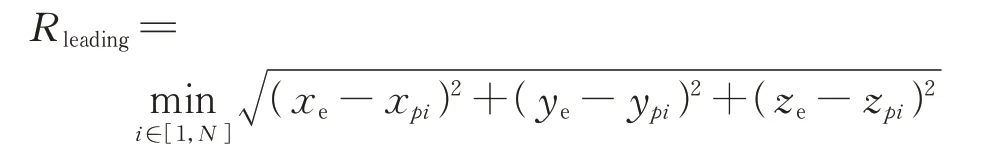
随着与捕获智能体愈近，给予逃逸卫星更大的惩罚；同时加入了时间奖励＞0，表示博弈持续时间越长，智能体卫星得到的奖励越大；、、分别为捕获惩罚、引导奖励、时间惩罚的权重系数，可针对不同任务进行调整。

4 MADDPG 算法

4.1 强化学习算法

本文实验针对同步轨道的集群卫星追逃博弈场景进行了设计。假设有一个3 卫星编队在轨道高度为42 249 137 m 附近运行（7.270 1×10），在相对坐标系500 m×500 m×500 m 空间内（训练时位置速度随机设定）遇到了轨道根数相似的一颗非合作目标卫星，实施追逃博弈方案。

为了使实验更具可操作性，设定逃逸卫星机动能力比追捕卫星机动能力大，即/=1.2，同时，规定=10 m，=0.5 m/s 为距离和速度的安全约束，当其中有一个追捕卫星靠近了逃逸卫星该距离和速度的约束值内时，博弈结束，追捕成功，每次博弈时间上限为1 000 s。由于在相对轨道系下进行博弈训练，因此在忽略高阶项后系统环境满足C-W 方程，而在C-W 方程中，耦合较为紧密的是、轴，这也是系统的复杂点，为加快收敛，忽略轴的动力学模型。假设追捕卫星和逃逸卫星均在一个轨道面运行，得到一个轨道面内二维的博弈场景。

本文实验平台：CPU 为intel-10500，内存8 GB×2，显卡为GTX1660。针对以上场景进行训练。

4.2 结果分析

通过以上的实验设计，在合理调整奖励函数的权重值，针对简化后追逃博弈模型进行训练后，算法达到了收敛。追捕卫星整体的奖励收敛过程效果如图5 所示。

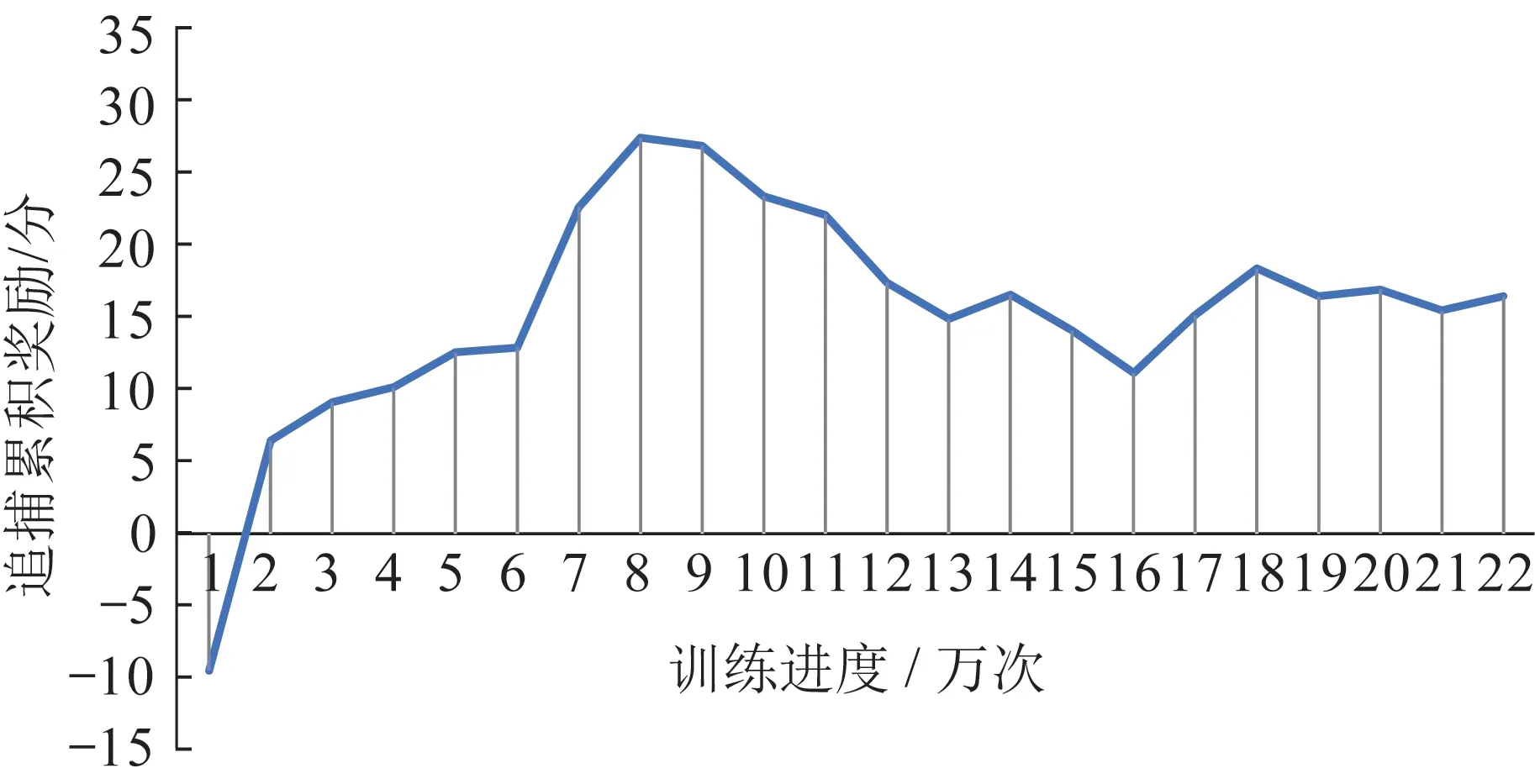
图5 追逃博弈训练奖励收敛过程效果Fig.5 Results of the reward convergence process of pursuit-evasion game training

在图5 中，随着博弈的进行和追逃博弈双方策略的不断优化，奖励值有3 个阶段的变化趋势与特点：在一开始，博弈双方策略均未能生成，可以理解为随机进行博弈奖励，由于追捕智能体具有数量优势，因此先找到了一定的联合策略进行优化，此阶段使得追捕智能体奖励值保持增加；随着回合的增加，逃逸智能体逐渐利用到了机动性能的优势，开始生成一定的逃逸策略，由于追捕智能体生成的“初级协同策略”开始失效，使得追捕智能体奖励函数值持续下降；随着博弈的继续进行，追捕智能体逐渐开始针对逃逸智能体优化其协同追捕策略，而逃逸智能体也利用自身机动优势针对追捕智能体的追捕策略进行逃逸策略的优化，因此奖励值在不断的波动中。最后，双方的策略在一定范围内实现动态平衡，得到最优或者次最优的追捕和逃逸策略。

各个智能体完成了集中训练，分散开始执行策略时，博弈策略验证时“涌现”出来了一系列的智能协同追逃博弈现象，主要有以下4 类，如图6 所示。

图6 “涌现”的智能博弈行为Fig.6 Emergent intelligent pursuit-evasion game behaviors

1）协同围捕。“协同围捕”现象在验证时最为常见，典型特点为多个追捕智能体按照不同方向靠近逃逸智能体，实现对逃逸智能体的“包围”，通过缩小范围完成追捕策略。

2）智能拦截。“智能拦截”的现象多出现在当逃逸智能体在一个方向逃逸机动时，追捕智能体协同运动至其逃逸方向上，实现拦截，当位置速度小于阈值时使得追捕博弈成功。

3）合作追逐。“合作追逐”的场景更具可观赏性，追捕智能体并不是单单从距离上靠近实现协同追捕，而是有计划地在逃逸智能体的其他方向上进行运动干扰，参与追捕博弈的智能体也不单单只是实现追捕的目的，有些智能体是以合作者的身份进行博弈，最终完成协同追捕任务。

4）预测潜伏。“预测潜伏”为这样一类场景和策略：当逃逸智能体试图通过机动优势“飞掠”过追捕智能体时，追捕智能体采取应对策略，先伪装成其他方向的机动，当逃逸智能体靠近以后，再改变机动方向，实现预测和潜伏的行为，最终实现追捕博弈。

5 结束语

本文面向空间多对一非合作目标追逃博弈场景进行了调研和分析，通过对博弈场景进行建模，在考虑最短时间、最优燃料以及碰撞规避的情形下进行奖励函数的塑造和改进，利用MADDPG 的方法进行集中训练，得到各个追捕卫星和逃逸卫星的最优追逃策略参数；然后分布式执行，使得多个追捕卫星和逃逸卫星之间能够完成追逃博弈。仿真结果表明，该方法能够完成集群卫星对非合作目标的追逃博弈，且能够利用数量优势有效地弥补速度劣势，涌现出“拦截”“围捕”“潜伏”“捕 获”等一系列智能博弈行为，有效地实现了博弈的目的，为卫星实施多对一非合作目标轨道追逃博弈的方法提供了一定的参考意义。