“多对多”模式下GEO 卫星在轨加注任务规划

韩 鹏，李兴龙，李传江，智 慧

（1.哈尔滨工业大学 航天学院，黑龙江 哈尔滨 150001；2.上海宇航系统工程研究所，上海 201109）

0 引言

近年来，随着人类太空探索活动的不断增加，在轨服务技术得到了大量关注。利用在轨服务技术可以极大地延伸各类在轨航天器的运行寿命，大大提高了经济效益。在轨加注作为在轨服务技术中的一种，同样受到了广泛的关注，并取得了长足的发展。许多国家相继完成了在轨加注任务的在轨实验验证，如我国的“天源一号”、美国的“任务延寿飞行器”等。现有的在轨加注模式多为“一对一”加注，其仍具有较高的成本。未来，随着航天技术的发展和对在轨服务运营成本的进一步控制，在轨加注的模式将由“一对一”逐步发展成为“一对多”“多对多”的加注模式，这就对在轨加注的任务规划和轨道机动优化带来了进一步的挑战。

运行在地球同步轨道的卫星通常具有高价值、高成本的特点，承担着预警、通信、气象检测等重要任务。因此，为同步轨道卫星设置在轨加注系统，以延长其服务寿命是非常必要且具有经济效益的。

许多学者针对不同模式下的在轨加注任务规划问题展开了研究。欧阳琦等率先研究了“多对多”场景下地球同步轨道（Geostationary Earth Orbit，GEO）卫星的在轨加注任务规划问题，采用遗传算法（Genetic Algorithm，GA）对问题进行求解；ZHANG 等在考虑J2 摄动和时间窗口约束的前提下，研究了同一轨道上服务星为目标星实施在轨加注的任务规划问题；ZHOU研究了“太空站-服务星-目标星”模式下的GEO 卫星在轨加注任务规划问题，并通过两组典型算例验证了算法的有效性；在文献［8］的基础上，文献［9］进一步研究了具有多个太空站的GEO 卫星在轨加注任务规划问题，仿真结果表明，所提出的算法能适用于规模更大的问题；CHEN 等研究了将P2P（Peer-to-Peer）与“多对多”模式相结合的混合策略下的在轨加注任务规划问题；文献［11］研究了服务星和目标星相互协作，同时展开轨道机动模式下的在轨加注问题，仿真实验表明，协作模式相比常规的“多对多”模式更加节省燃料。

综合以上文献，不同学者针对在轨加注场景提出了多种加注模式，包括“太空站-服务星-目标星”模式、P2P 模式、“服务星-目标星相互协作”模式等。基于现有的航天技术，实现复杂的在轨加注模式难度较大，且成本较高，因此，“一对多”“多对多”的在轨加注模式仍是最具可行性的在轨服务模式，研究“多对多”模式下的在轨加注任务规划问题仍具有重要意义。本文将借鉴VRP（Vehicle Route Planning）问题中的建模方式，将“多对多”在轨服务场景表示为一张完全有向图，基于完全有向图建立在轨加注任务规划模型，并在此基础上，给出轨道转移燃料消耗计算模型。

现有文献中，任务规划问题的求解算法多基于元启发式智能优化算法，并针对问题特性对算法进行适当改进，如遗传算法、粒子群算法、蚁群算法等。这类算法的特点是灵活性强，便于处理各类复杂的约束条件，但存在局部搜索能力较差、易陷入局部最优的缺陷。针对以上缺陷，本文基于遗传算法，设计了一种将大邻域搜索（Large Neighbourhood Search，LNS）算法和遗传算法相结合的混合启发式算法（Large Neighbourhood Search-Genetic Algorithm，LNS-GA）。该算法利用大邻域搜索算法中的“破坏”和“修复”思想，对遗传算法每一代种群中的精英个体进行进一步的迭代搜索，从而增强算法的局部搜索能力。最后，通过仿真对比实验验证了本文所提出算法的有效性和优越性。

1 任务规划模型建立

1.1 “多对多”在轨加注任务场景描述

如图1 所示，在“多对多”在轨加注任务场景中，若干个燃料消耗殆尽的目标卫星运行于GEO 圆轨道，每个目标卫星具有确定的燃料加注需求，但其轨道半长轴、轨道倾角、升交点赤经、定点经度等参数存在差异。若干个规格完全相同的服务航天器被同样部署至GEO 圆轨道上，其携带固定容量的燃料，燃料可加注给目标卫星，也可用于自身轨道机动。每个服务航天器干重相同，并且携带1 台比冲固定的发动机用于变轨。服务航天器需依次转移至目标卫星附近，与目标卫星完成对接，并为其加注燃料。在完成既定任务后，服务航天器离开目标卫星进入停泊轨道待命。进行任务规划的目的是为每个服务航天器预先确定最优的服务目标和服务顺序，在保证所有目标卫星均可被加注燃料的前提下，最小化服务所有航天器的燃料消耗。

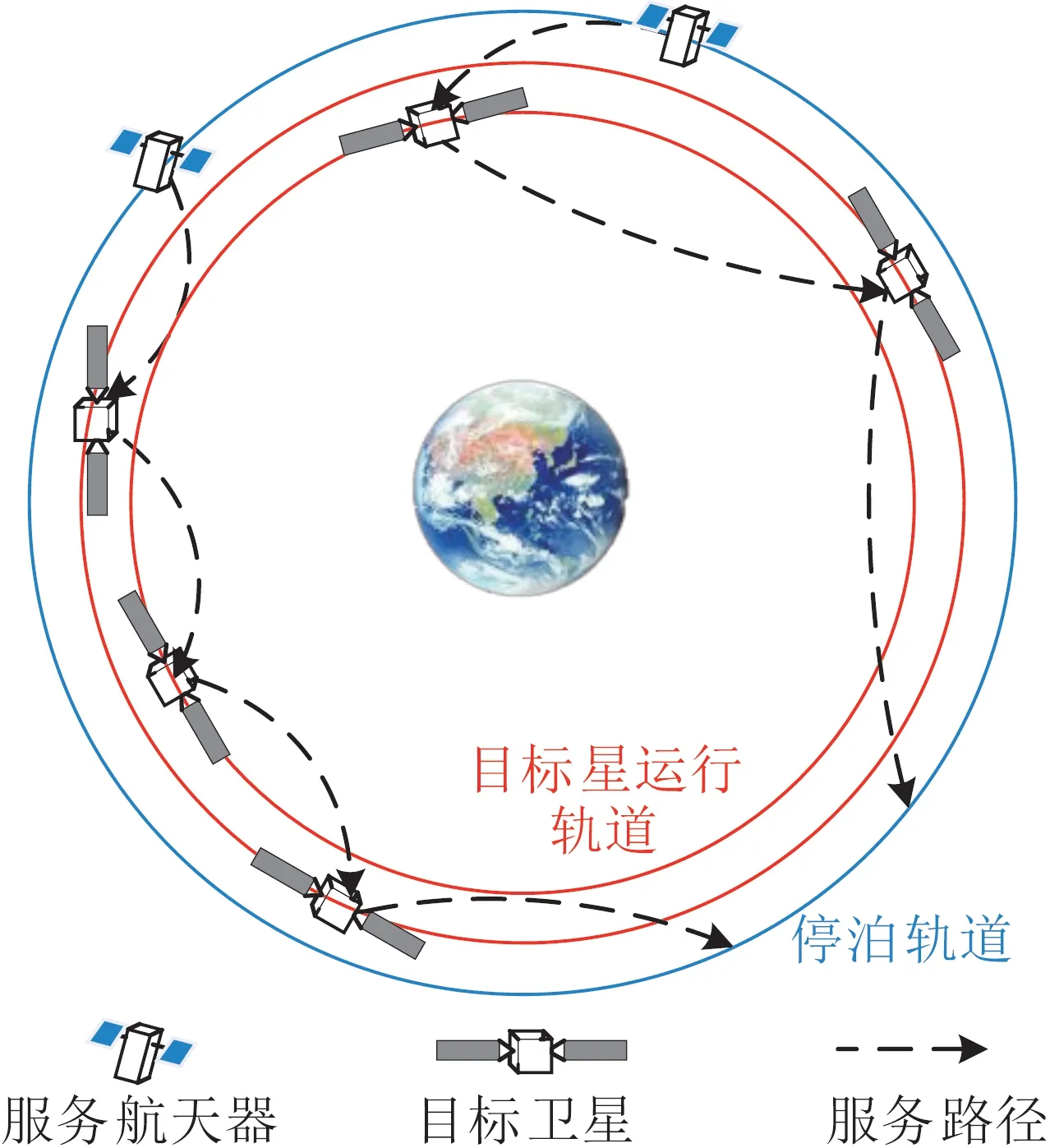
图1 “多对多”在轨加注任务场景Fig.1 Many-to-many on-orbit refueling mission scenario

1.2 任务规划模型

如图2 所示，可将“多对多”在轨加注场景中的所有服务航天器和目标卫星表示为一个完全有向图=(，)。其中，为节点集合，包括目标节点集合、服务航天器初始节点集合和虚拟结束点；为连接所有节点的边的集合。一组规模相同的服务航天器由集合表示，其规模与相同。

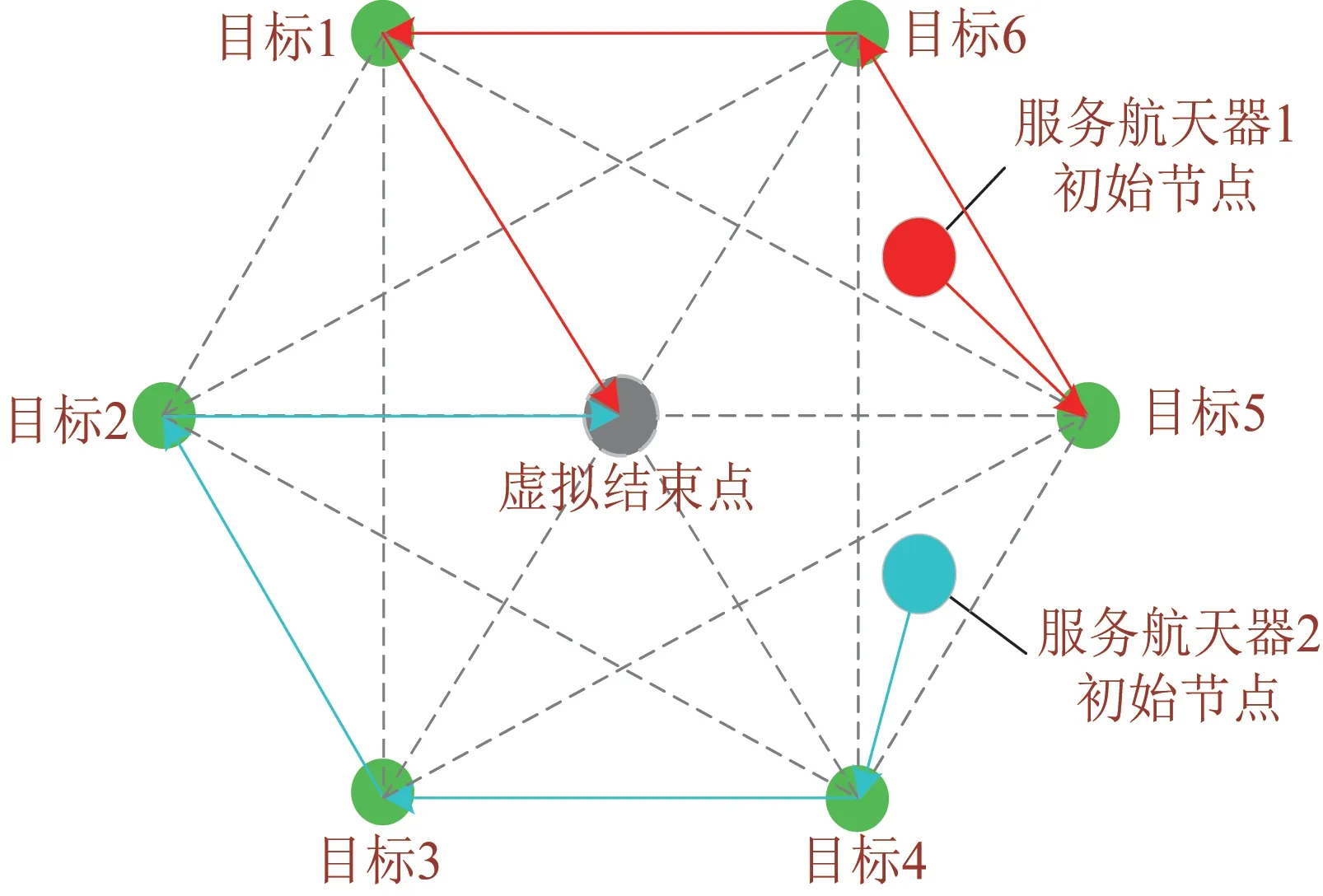
图2 完全有向图表示的“多对多”在轨加注场景Fig.2 Fully directed graph for the many-to-many on-orbit refueling scenario

服务航天器需从初始节点出发，依次机动至多个目标点附近为其进行在轨加注，最后到达虚拟结束点，结束任务。每个服务航天器在初始节点处的最大燃料均为，所携带的燃料可用于在轨加注和轨道转移，每个服务航天器必须在燃料用尽前完成所有既定的在轨加注任务。每个目标卫星只能且仅可被一个服务航天器服务一次。对于目标卫星，其燃料需求为d。服务航天器从目标点转移至的燃料消耗为c，c的计算将在1.3 节中叙述。定义决策变量x，该变量表示服务航天器是否服务完成目标点后继续服务，若是，则x=1，否则x=0。通过对决策变量的优化，实现在满足路径约束和服务航天器燃料约束的前提下，使得所有服务航天器的燃料消耗之和最小。

基于以上定义，则可得到“多对多”在轨加注的任务规划模型。

1）决策变量：x，∀∈，∈，∈。

2）目标函数：

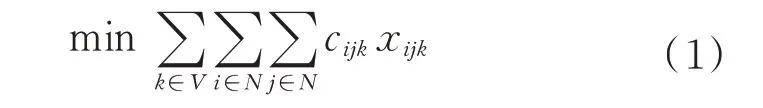
3）约束条件：

上述公式中：式（1）为规划模型的目标是最小化所有服务航天器的燃料消耗；式（2）确保了每个目标仅可被一个服务航天器进行一次在轨加注；式（3）确保服务航天器无法转移至任意初始节点；式（4）和式（5）为从每个服务航天器初始节点仅可出发一个与其编号相同的服务航天器；式（6）保证了每个航天器维修路径的连续性；式（7）为每个航天器最终必须转移至虚拟结束点；式（8）为从任意节点到虚拟结束点的燃料消耗为0；式（9）保证每个航天器的总燃料消耗不超过其携带的最大燃料；式（10）为决策变量的取值约束。

1.3 轨道转移燃料消耗模型

服务航天器欲在完成目标的加注后通过轨道转移至目标附近，为进行燃料加注。服务航天器与目标所处轨道分别为{，，}、{，，}，其中，为轨道半长轴，为轨道倾角，为升交点赤经。服务航天器采用霍曼变轨方法消除与目标卫星的半长轴之差，并且，在合适的时机实施霍曼变轨，还可消除两航天器的相位之差。霍曼变轨需要的速度增量为

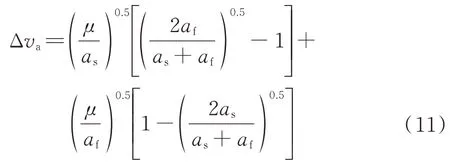
式中：为地球引力常量，通常取=3.986×10km·s。

两航天器之间还存在轨道面的差异，其轨道面夹角由轨道倾角和升交点赤经共同决定，可由如下公式计算得到：

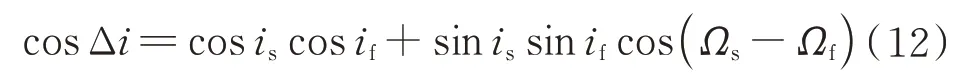
因此，服务航天器消除轨道面差异所需的速度增量为

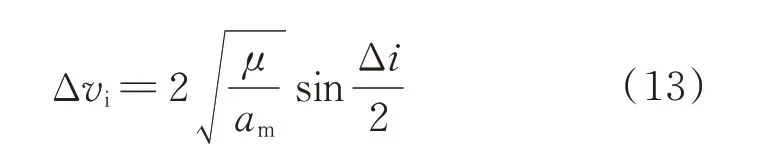
式中：=max {，}。

综上，可得服务航天器与目标卫星交汇的所需的总速度增量为

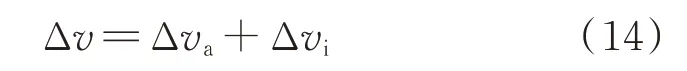
进一步，服务航天器从目标转移至目标的燃料消耗为

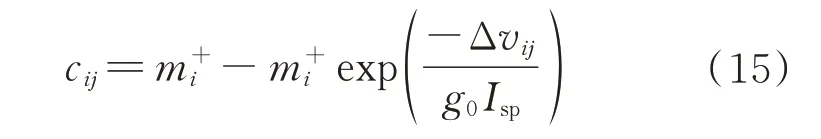
2 求解框架设计

“多对多”在轨加注任务规划问题为一类典型的整数规划问题，当问题规模较大时，其通常呈现NP-Hard （Non-deterministic Polynomial Hard）特性。求解这类问题较为常用的算法为元启发式算法，如遗传算法、蚁群算法、粒子群算法等。遗传算法由于其较强的全局搜索能力，近年来被广泛应用于各类优化问题中，本文拟采用遗传算法作为主框架来求解任务规划问题。同时，考虑到遗传算法缺乏局部搜索机制，因此，将大邻域搜索算法与遗传算法相结合，取长补短，设计了一种LNS-GA 算法，以增强算法的局部寻优能力。以下将详细介绍算法的具体流程。

2.1 遗传算法设计

遗传算法的设计通常包括3 部分：编码解码规则的设计、遗传算子（选择、交叉、变异算子）的设计、适应度函数的设计。

本文采用序列编码方式对决策变量x进行编码，设共有个服务航天器和个目标卫星，则染色体长度固定为=+-1。染色体由取值为1～的互不相同的基因构成，其中，取值为1～的基因代表目标卫星的服务顺序，取值(+1)～的基因为分割位，将整个染色体分割为个部分，每个部分代表一个服务航天器的在轨加注顺序。例如，对于5 个目标卫星和2 个服务航天器的情况，一个可能的染色体5-3-1-6-2-4，该染色体含义为服务航天器1 依次对目标5、目标3、目标1 进行在轨加注；服务航天器2 依次对目标2、目标4 进行在轨加注。

遗传算子包括选择、交叉、变异算子。对于选择算子，本文采用精英保留策略和轮盘堵转法完成，即对于种群中适应度函数最大的染色体，直接保留至下一代参与子代个体的生成，对于剩余染色体通过轮盘赌的方法进行筛选。交叉算子采用部分映射交叉法，即对于参与交叉过程的2 个染色体，随机选择2 个基因点位，将基因点位间的染色体进行互换，之后，消除每个染色体中的重复基因即可完成交叉过程，每个染色体以固定概率确定其是否参与交叉过程。变异过程针对单个染色体，对于进行变异的染色体，随机选取2 个基因点位，将其基因进行互换即可，每个子代参与变异的概率为。

适应度函数用于衡量每个染色体的可行解对应指标函数的大小和对约束条件的适应程度，因此，通常由指标函数项和违反约束条件的罚函数项组成。基于本文所述的序列编码方式，其得到的可行解总是满足式（2）～式（7）和式（10），需要利用适应度函数对式（9）进行评估，因此，适应度函数可设为

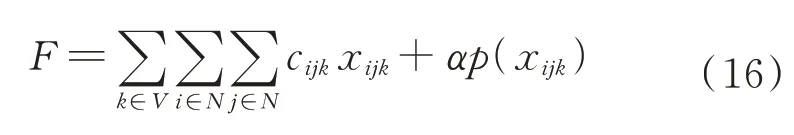
式中：为惩罚系数；(x)为惩罚项，

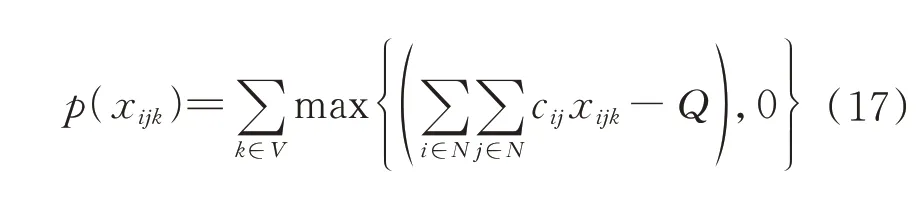
2.2 大邻域搜索算法设计

大邻域搜索算法（Large Neighborhood Search，LNS）由SHAW 在1999 年首次提出，是一种局部搜索算法，被广泛应用于各类路径规划和取货-送货等问题中，均取得了良好的效果。其基本思想是通过对可行解的“破坏”与重新“修复”而得到新的可行解，完成搜索寻优过程。设计LNS 算法的关键是可行解“破坏”与“修复”规则的设计。

2.2.1 可行解“破坏”进程

对当前可行解进行破坏的过程是按照一定规则移除现有服务序列中固定数量的目标卫星。本文中，通过依次移除与已被移除目标相关性最大的目标完成可行解的破坏。

对于目标和，两者相关性定义为

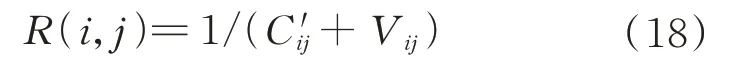
式中：V为目标和是否被同一服务航天器加注燃料，

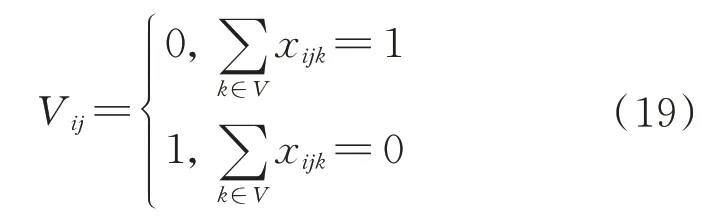
C′为服务航天器从到的“代价”。由于实际的燃料消耗与服务航天器进行轨道转移前的质量相关，难以快速计算，因此，采用归一化后的轨道转移速度增量表征两目标间的转移代价：

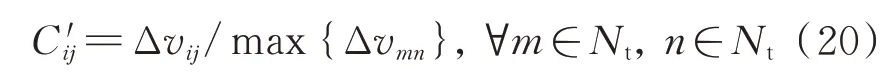
值得注意的是，每当从现有序列中移除一个目标后，均需要更新剩余目标和移除目标的相关性。

2.2.2 可行解“修复”进程

可行解的“修复”进程是只将由“破坏”进程移除的目标按照一定的规则重新插入到已有序列中，形成对原有问题的可行解。本文的插入方法将基于最远插入启发式规则，优先在现有序列插入最小Δ增量最大的待插入目标卫星。待插入目标的最小Δ增量是指，将目标插入现有序列任意位置中，插入前后服务序列总Δ增量最小的位置为最小Δ增量插入位置，对应的Δ增量为对应待插入目标的最小Δ增量。具体步骤如下：

对于任意待插入目标，先找出满足时间约束的所有插入点，再分别计算上述插入点的Δ增量；

找出上述插入点中Δ增量最小的最佳插入点，并记录Δ增量；

对于所有待插入目标重复执行步骤1～步骤2；

找到最小Δ增量最大的待插入目标，将该目标插入至最佳插入点，并更新待插入目标集；

重复步骤1～步骤4，直到所有目标完成插入，形成新的可行解。

2.3 LNS-GA 算法框架

LNS-GA 算法的整体框架如图3 所示。该框架中，将遗传算法作为外层算法，以充分利用其全局搜索能力。

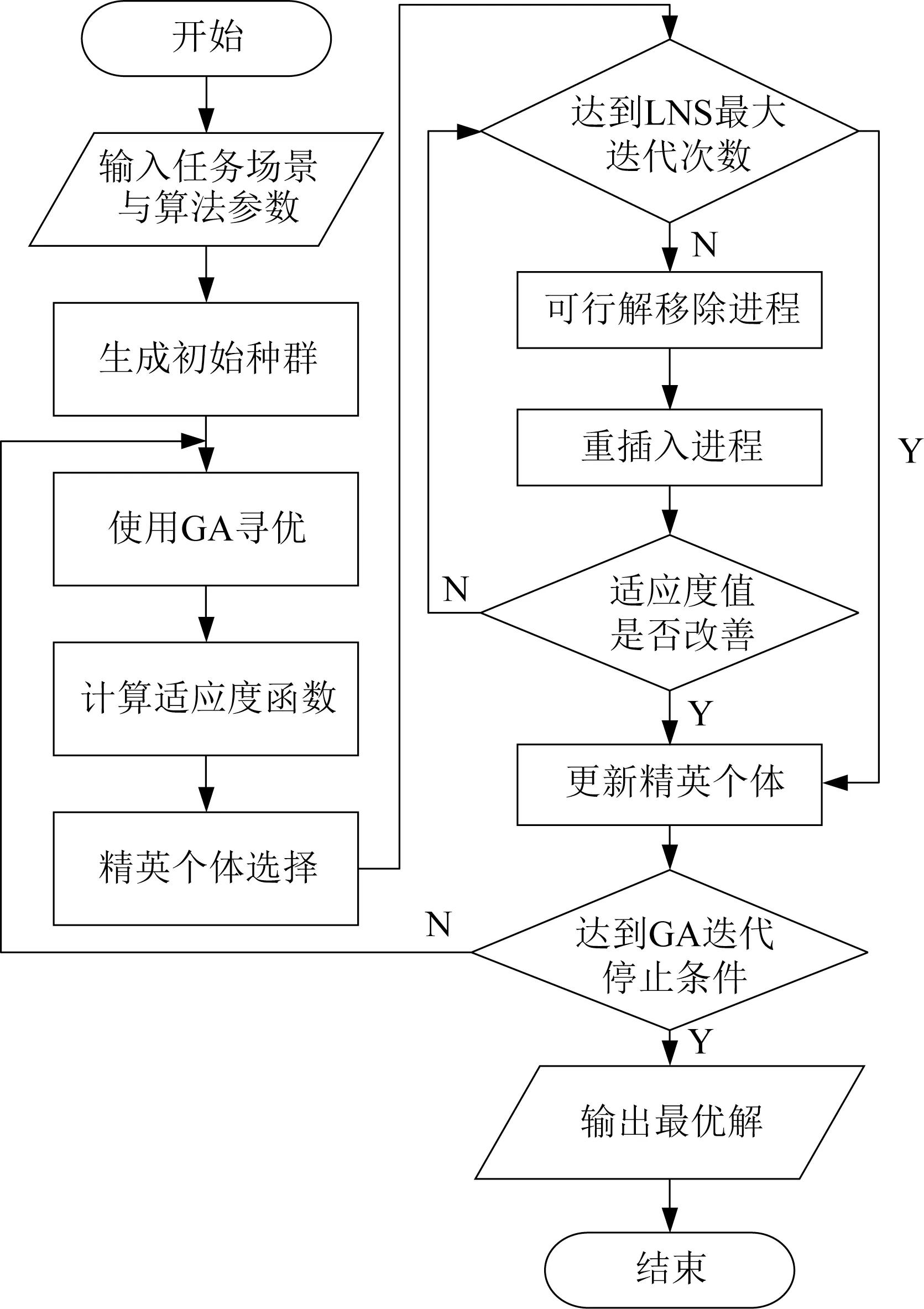
图3 LNS-GA 算法流程图Fig.3 Flow chart of the LNS-GA algorithm

由于LNS 算法流程复杂，运行耗时较长，无法对遗传算法得到的所有个体进行局部寻优，因此，在外层遗传算法完成一次迭代后，仅选取部分精英个体传递至内层的LNS 算法中，进行进一步的局部搜索优化。LNS 算法针对每个精英个体进行有限代数的迭代寻优，若在最大迭代次数内找到更优解，则提前结束算法，更新精英染色体；若在达到最大迭代次数后仍未找到更优解，也同样退出算法。更新后的精英个体也同样作为父代继续参与外层遗传算法的迭代，直到外层遗传算法达到其停止条件，算法停止。

3 仿真实验

为验证所提出的求解算法的有效性，本文设定了3 个服务航天器为30 个GEO 卫星进行在轨加注的场景。服务航天器参数见表1。30 个目标的轨道参数为随机设定，其轨道半长轴设定在42 000～42 500 km 之间，轨道倾角设定为0～5之间，升交点赤经设定为0～360之间。每个服务航天器本身的质量为1 000 kg，携带燃料质量为1 500 kg，变轨发动机比冲=3 200 m/s。每个目标卫星的燃料需求均设定为100 kg。分别采用LNS-GA 和标准遗传算法对问题进行求解，并将结果进行对比，两算法的参数设定见表2。算法的停止条件有两个，一个是迭代次数达到最小迭代次数，另一个是连续50 代的最优适应度值不发生变化。两算法得到的结果如图4～图7 所示。

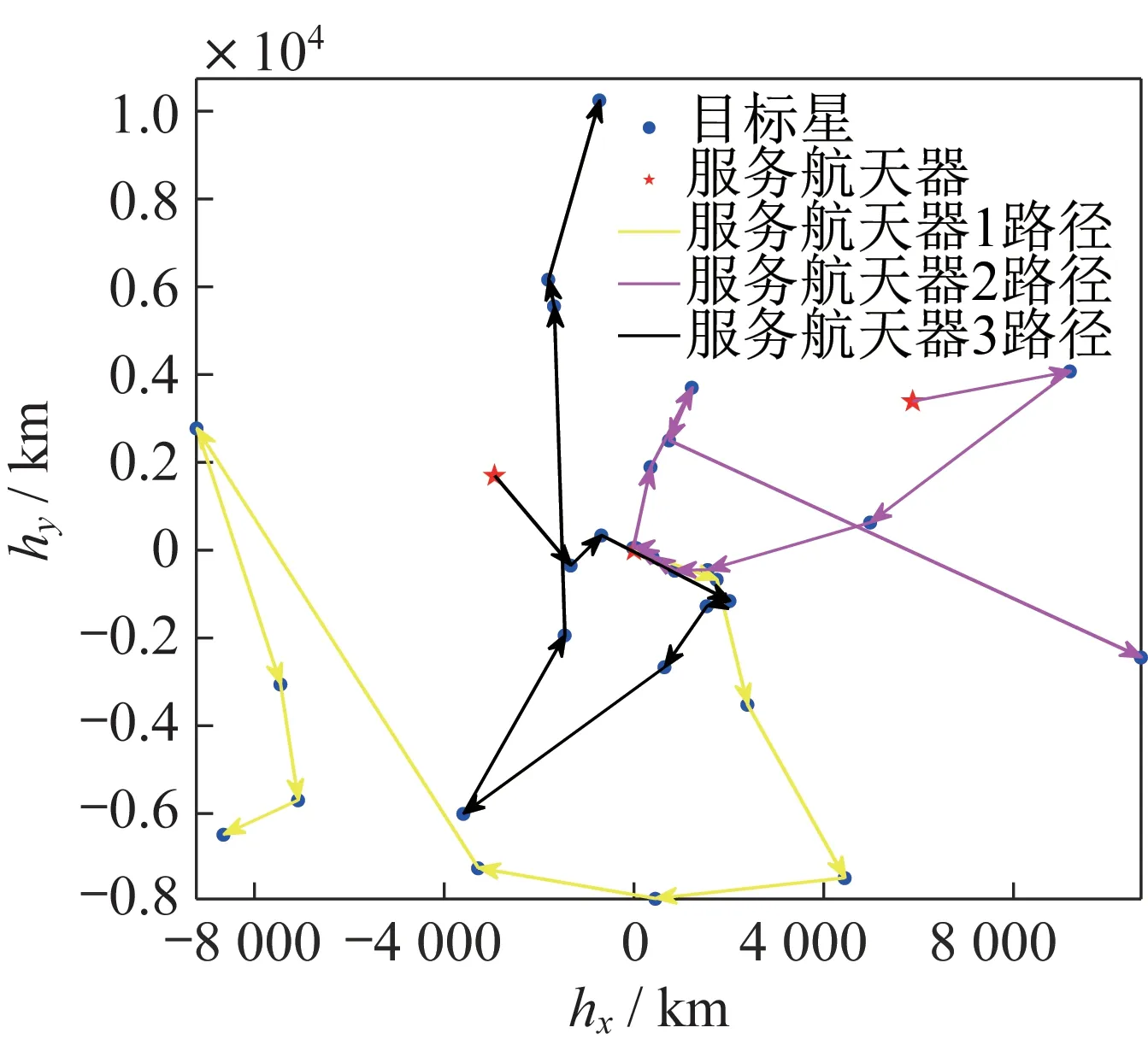
图7 遗传算法得到的任务规划路径Fig.7 Mission planning route obtained by the GA

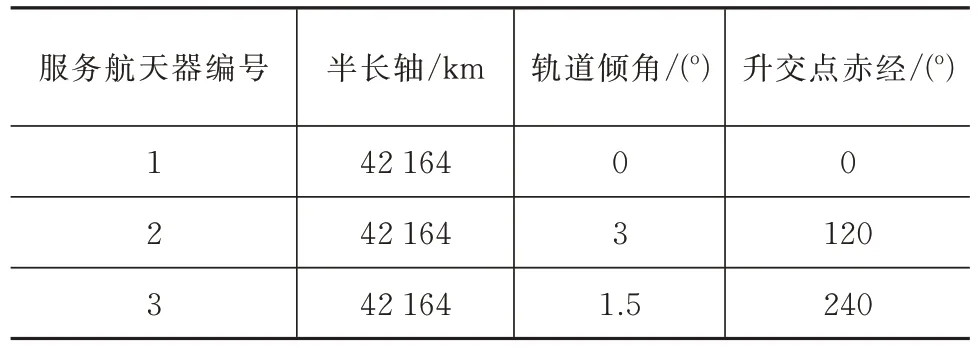
表1 服务航天器轨道参数Tab.1 Orbit parameters of the service spacecrafts

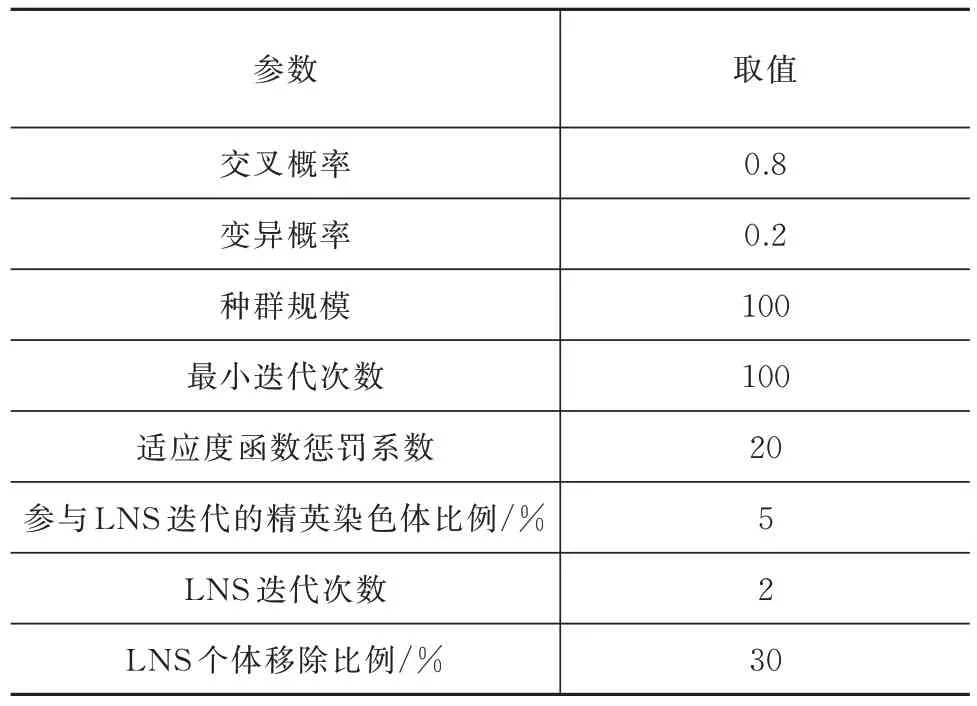
表2 算法参数设定Tab.2 Parameter setting of the algorithms

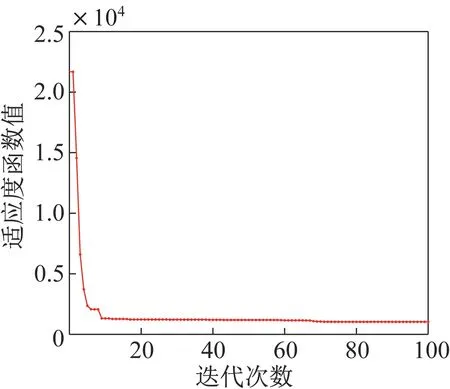
图4 LNS-GA 迭代曲线Fig.4 Iterative curve of the LNS-GA

图4～图5 分别为LNS-GA 和遗传算法的迭代曲线。可以看到，LNS-GA 在设定的最小迭代次数内便收敛至最优值，遗传算法在530 代的迭代之后才收敛。最终，LNS-GA 得到的适应度值为1 034.22，而遗传算法得到的适应度为1 311.65，因此可以看出，LNS-GA 在结果的最优性上明显好于传统的遗传算法，表明其具备更强的搜索能力。

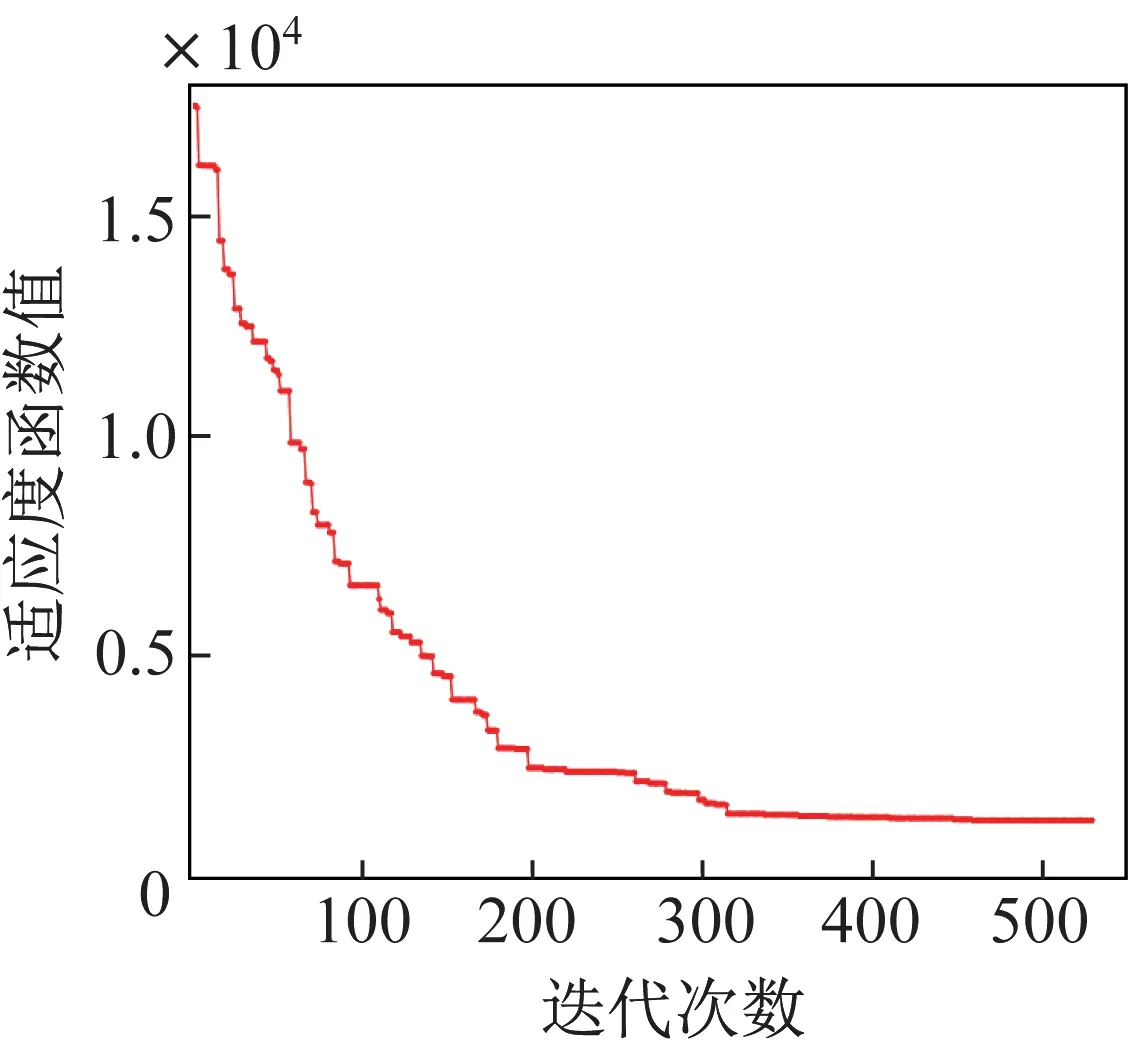
图5 遗传算法迭代曲线Fig.5 Iterative curve of the GA

图6～图7 分别为两种算法得到的规划结果中每个服务航天器的服务路径，图中表示的目标卫星和服务航天器均为其初始运行轨道的角动量在天赤道面的投影。卫星轨道角动量的投影分布一定程度上反映了不同卫星的轨道在轨道半长轴、轨道倾角、升交点赤经等参数上的差异。因此，坐标平面内两目标卫星之间的距离越大，表明服务航天器在两目标之间的转移的速度增量越大，而服务航天器燃料的消耗量也与其所需的速度增量成正比。服务航天器的最优服务顺序对应着在天赤道面上服务航天器依次为目标卫星完成在轨加注的最短路径。可以看出，由LNS-GA 得到的每个服务航天器的任务规划路径较为连续，没有互相交叉，路径总长度较短，燃料消耗较少；而GA 得到的规划结果中，单个服务航天器的规划路径存在交叉的情况，总体路径长度要长于LNS-GA 的规划结果，因此燃料消耗会更大。

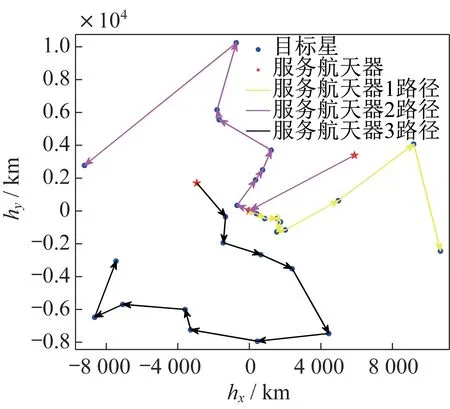
图6 LNS-GA 得到的任务规划路径Fig.6 Mission planning path obtained by the LNS-GA

两算法得到的规划结果的详细信息见表3。可以看到，LNS-GA 的规划结果中，在执行完成本次任务后，仍有两服务航天器燃料质量大于100 kg，存在进一步执行加注任务的能力，而遗传算法得到的规划方案中，所有服务航天器均丧失了进一步执行任务的能力，这进一步体现了LNS-GA算法的优越性。

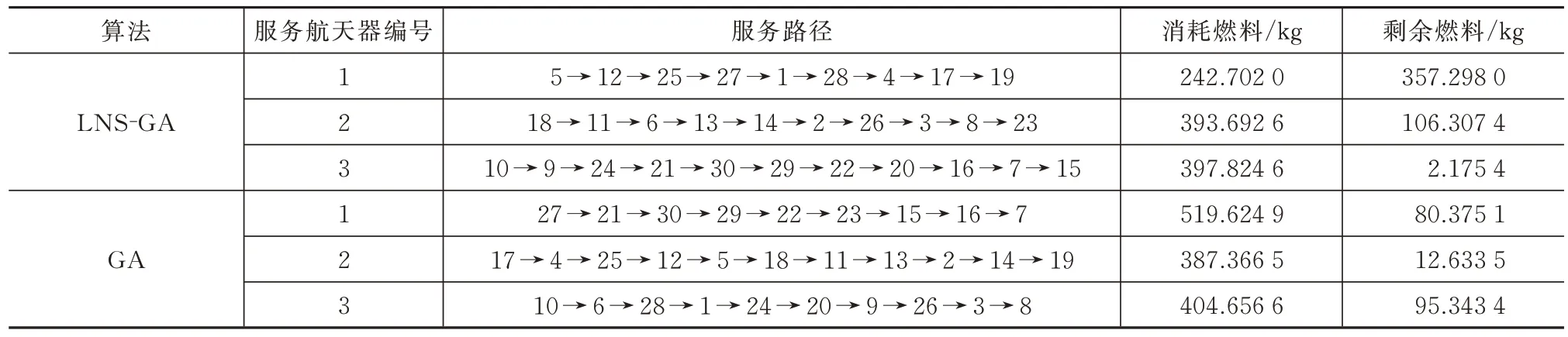
表3 两种算法得到的详细任务规划结果对比Tab.3 Detailed mission planning results obtained by the two algorithms

4 结束语

本文针对“多对多”模式下的在轨加注任务规划问题进行了研究，基于完全有向图给出了任务规划数学模型，同时给出了GEO 卫星间轨道转移燃料消耗的数学模型。为求解上述问题，在现有遗传算法的基础上设计了一种LNS-GA 混合算法，该算法相比遗传算法改进了局部搜索能力。最后通过仿真对比实验验证了所设计算法的有效性和优越性。后续的研究中，应着重考虑时间约束下的在轨加注任务规划问题的建模与求解。