材料因素对金属疲劳裂纹扩展的影响
刘斌超 王秋懿 杨蓉 鲁嵩嵩 鲍蕊
摘要:先进工艺和材料的发展往往突破了经典断裂力学理论中的宏观均匀各向同性材料假设,使得当前主要关注裂尖力学参数,仅以试验数据拟合参数来考虑材料因素影响的金属材料疲劳裂纹扩展分析方法难以适用。本文首先基于课题组近年来在金属材料疲劳裂纹扩展方面的研究,对材料因素导致的特殊疲劳裂纹扩展行为进行介绍,并对其机理进行分析和总结;然后,对当前疲劳裂纹扩展分析方法的逻辑思路进行分析,并指出相关研究的主要落脚点在于合理有效地考虑力学因素和材料因素的影响;最后,主要针对疲劳裂纹路径偏折的预测方法进行讨论,提出了一种疲劳裂纹扩展的净驱动力概念模型。本文的分析讨论有助于从力学因素与材料因素交互作用的角度来看待金属疲劳裂纹扩展问题,所得结论能够为先进工艺金属材料的疲劳裂纹扩展分析及相应结构的损伤容限分析評估提供指导。
关键词:疲劳裂纹扩展;裂纹偏折;裂纹分叉;材料组织;增材制造
中图分类号:V215.5文献标识码:ADOI:10.19452/j.issn1007-5453.2022.03.010
现阶段,飞机金属结构主要按照损伤容限理念设计,而疲劳裂纹扩展分析是损伤容限设计和评定中的一项重要工作。目前的疲劳裂纹扩展分析方法主要基于线弹性断裂力学理论,采用以Paris关系式为代表的模型来表征疲劳裂纹扩展速率,并通过积分得到初始裂纹长度到临界裂纹长度之间的疲劳裂纹扩展寿命。
上述疲劳裂纹扩展速率模型及方法对于宏观均匀各向同性的传统工艺金属材料结构具有较好的适用性;然而,先进材料的发展日新月异,这些材料突破了宏观均匀各向同性的特点,使得现有模型难以精细刻画其疲劳裂纹扩展行为。另一方面,在未来新工艺新型整体结构的应用[1]和数字孪生等虚实结合理念的实践[2]中,疲劳与损伤容限评估都是亟待解决和改进的重要问题,而对材料疲劳性能和疲劳裂纹扩展行为的有效表征则是其中的首要任务。因此,深入认识并有效表征材料因素对疲劳裂纹扩展的影响,对新工艺和新材料在飞机结构上的应用具有重要意义。
本文旨在启发看待材料因素对金属疲劳裂纹扩展影响的新视角,并为先进材料的疲劳裂纹扩展分析方法提供指导。本文首先系统介绍了课题组近年来的相关研究,然后对现有模型的逻辑思路和适用范围进行分析,最后对材料因素的影响及相应考虑方式进行讨论。
1材料因素导致的特殊疲劳裂纹扩展行为
本部分内容主要基于课题组近年来在疲劳裂纹扩展方面的研究工作,重点介绍由材料因素导致的特殊疲劳裂纹扩展行为,并对机理进行分析、讨论和总结。
1.1裂纹偏折:激光熔化沉积TC18钛合金
激光熔化沉积是一种增材制造工艺,其工艺流程特点将导致TC18钛合金呈现柱状晶和等轴晶两种宏观材料组织周期性排布的特点,如图1所示。其中,柱状晶内的α片层在广阔区域内呈定向排布,而单个等轴晶内α片层虽然定向排布,但广阔区域内其取向呈准随机排布。
这种特殊的材料组织排布特征将对疲劳裂纹扩展的路径和速率产生显著影响[3-4],如图2所示。当裂纹初始方向垂直于柱状晶方向时,宏观疲劳裂纹将明显偏离于I型裂纹路径而呈现显著的大角度偏折,且这种偏折在柱状晶中更加明显。

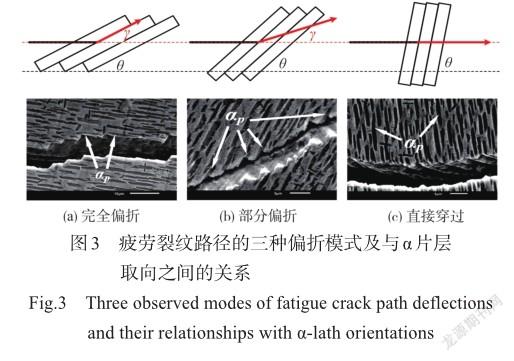
进一步研究发现,这种疲劳裂纹扩展行为受到α片层取向的影响。图3表明,疲劳裂纹偏折呈现出三种模式:当α片层取向角θ较小时,疲劳裂纹倾向于沿α片层扩展,呈现“完全偏折”模式;当α片层取向角θ较大时,疲劳裂纹偏折角度小于α片层取向角θ,呈现“部分偏折”模式;当α片层取向角θ几乎与裂纹方向垂直时,疲劳裂纹几乎不偏折,呈现“直接穿过”模式。
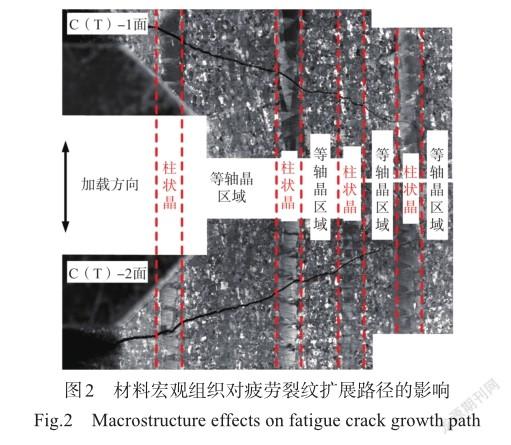
在α片层定向排布的柱状晶中,由于疲劳裂纹倾向于沿着较脆的α/β相界扩展,因此其路径在柱状晶中会发生明显偏折;在α片层取向宏观准随机排布等轴晶区域中,虽然疲劳裂纹也倾向于沿着较脆的α/β相界扩展从而发生偏折,但这种偏折仅限于微细观尺度而不会显著地体现到宏观尺度上。总的来说,由于α片层的排布特点,激光熔化沉积 TC18钛合金中的柱状晶具有明显的各向异性、等轴晶区域表现出准各向同性,而这种材料组织的不均匀性和各向异性将影响疲劳裂纹的扩展模式,进而导致疲劳裂纹扩展性能的不均匀性和各向异性。
此外,疲劳裂纹扩展速率也会随路径偏折发生变化,试验中则既观察到速率加快也观察到速率降低,但一般是速率加快,这与经典断裂力学理论分析结果相违背,具体原因将在第3节中进行分析。
若采用传统分析方法,试件几何和载荷条件都是对称的,其疲劳裂纹路径也一定是对称的,因此无法解释或预测这种显著的宏观偏折现象。这是因为这种特殊的疲劳裂纹扩展行为是由材料因素导致的,而传统方法中缺乏对材料组织不均匀性和各向异性的考虑。另一方面,传统分析方法中的速率模型(如Paris关系式)由于缺少对于材料组织不均匀性和各向异性的考虑,因此也就无法对速率变化做出有效表征。
1.2裂纹分叉:2324-T39铝合金
20世纪80年代前后,美国铝业公司开发出2324-T39铝合金。与传统2024铝合金相比,它断裂韧性显著提高、疲劳裂纹扩展速率相对较低,因此具有较优的损伤容限性能,被认为是机翼下表面蒙皮的合适材料。
2324-T39铝合金经过轧制后,其晶粒形貌呈现一定方向性,如图4所示。具体来说,晶粒在L方向较为细长,而在S方向长度较短;在实际使用中,2324-T39铝合金往往制成薄板,裂纹一般在L-T面内扩展,其中加载方向沿L向、裂纹扩展沿T向。

采用飞-续-飞基准谱(S0)和飞-续-飞五级截除谱载荷(S1~S5),对L-T方向2324-T39铝合金中心裂纹板试件(即M(T)试件)进行疲劳裂纹扩展试验,如图5所示。可以看到,在S0~S3谱载荷下,疲劳裂纹平直扩展,符合I型裂纹路径;而S4和S5两种截除水平谱载荷下,疲劳裂纹将显著偏离I型路径[5-6]。此外,对S5截除水平谱载荷进行了多件试样的疲劳裂纹扩展试验,均出现了这种特殊路径现象。
一方面,和1.1节中激光熔化沉积TC18钛合金疲劳裂纹路径偏折相似,在试件几何及载荷条件满足对称性的情况下,发生这种特殊的路径变化显然是受到材料组织的影响;另一方面,疲劳裂纹路径是否发生特殊变化还与循环载荷特征有关,表明路径变化不单单受材料因素的影响,还受到力学因素(更准确地说是载荷因素)的影响。
这表明,疲劳裂纹扩展的具体行为是力学因素和材料因素交互作用的结果:在满足一定条件的情况下,材料因素的作用被限制在微细观尺度,宏观尺度的疲劳裂纹扩展行为符合经典断裂力学理论;而在一些特定条件的情况下,材料因素的作用能够表现到宏观尺度上,使得疲劳裂纹扩展模式偏离于经典断裂力学理论。

图6更清晰地展示了S5截除水平谱载荷情况下疲劳裂纹的宏观形貌及其形成过程。可以看出,这种裂纹路径是由一种二次裂纹所引起的裂纹分叉过程导致的:某刻主裂尖附近出现二次裂纹,随后二次裂纹与主裂纹连通,二次裂纹成为新的主裂纹并继续扩展,宏观上发生裂纹分叉和偏折。这种裂纹分叉现象易于在施加高载时出现,且二次裂纹一般萌生于塑性区边界的晶界处,如图7所示。
特别地,对T-L方向取样的试件进行疲劳裂纹扩展试验,也会出现类似的裂纹分叉现象,但由于T方向晶粒长度较短,因此这种分叉对宏观裂纹路径的作用不明显,即宏观尺度的裂纹路径要比L-T方向平直得多。
总的来说,2324-T39铝合金这种裂纹分叉行为是由力学(载荷)因素与材料因素的交互作用导致的,而由于宏观疲劳裂纹扩展模式不满足经典断裂力学理论,因此传统分析方法无法解释或预测这种现象。
1.3裂纹分叉:7050-T7451铝合金
在L-S方向,7050-T7451铝合金的疲劳裂纹扩展试验中还观察到了另一种形式的裂纹分叉现象,如图8所示,疲劳裂纹可能产生小角度分叉(branching)现象,也可能产生几乎垂直于扩展方向的大角度分叉(Splitting)现象。甚至在剩余强度试验中也会稳定地出现这种大角度分叉现象[7],其断裂模式明显不符合经典断裂力学理论,如图9所示。



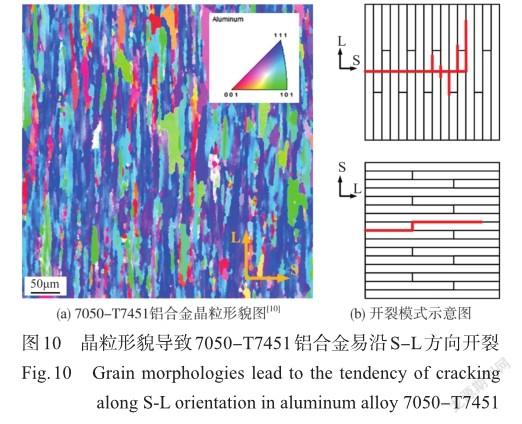
显然,这种现象也是由材料组织导致的,如图10所示,7050-T7451的晶粒呈长条状,其L方向晶粒长度显著长于S方向,而裂纹容易沿S方向晶界开裂,因此导致上述大角度分叉现象。作为补充,在具有类似晶粒形貌的其他2系和7系铝合金中,也有文献报道了类似的裂纹分叉行为[8],甚至在2297铝合金的光滑试样疲劳试验中也发现了大角度裂纹分叉现象[9];从文献中的结论来看,研究者基本达成共识,即都认为该问题是由材料组织特征引起的,但还没有找到合适有效的方法来表征或评估材料组织形貌的影响。
从上述研究案例可以看出,无论是传统工艺铝合金还是增材制造钛合金,只要其材料组织呈现出一定的不均匀性和各向异性,其宏观疲劳裂纹扩展行为往往会呈现出经典断裂力学理论难以解释的特殊现象。因此,后文将首先对现有基于线弹性断裂力学的裂纹扩展速率模型进行分析和讨论,指出未来研究所需要关注的重点。
2现有疲劳裂纹扩展模型的特点 2.1基于线弹性断裂力学的裂纹扩展速率模型逻辑分析

虽然Paris关系式的形式很简单,但却能够充分体现出研究者对疲劳裂纹扩展的认识。目前公认的是,Paris关系式的重大意义在于将线弹性断裂力学引入了疲劳研究,具体来说就是采用了应力强度因子这样一个力学参数。金属疲劳裂纹扩展分析中断裂力学参数的引入,奠定了损伤容限评定思想的理论基础,改变了飞机结构保安全的设计评定策略,具有划时代的意义。
然而在Paris关系式提出时,却受到了当时学者的批评,这种批评认为疲劳裂纹扩展是一个塑性驱动的过程,因此采用线弹性断裂力学参数来表征不符合力学逻辑。后续实践表明,Paris关系式在恒幅载荷条件下适用性很好,其形式简单、方便好用的特点受到了工程界的青睐;但对于变幅载荷和谱载荷等材料塑性起主要作用的情况,则还需要通过合适的迟滞模型来表征疲劳裂纹扩展速率的变化。
从本质上讲,Paris关系式是一种基于试验数据的关联关系(correlation):对应疲劳载荷循环的应力强度因子变程ΔK与裂纹扩展速率的关联关系,而非从机理上来解释疲勞裂纹为何扩展和如何扩展。
此外,采用应力强度因子K(变程ΔK)来关联疲劳裂纹扩展速率,需要认识到如下几个方面。
(1)K本质上通过裂尖变形场推导得到,而工程上往往通过载荷特征和几何特征计算得到,因此这个过程暗含了宏观均匀各向同性的材料假设。

(3)K是一个线弹性力学参数,采用该参数的前提条件是塑性作用可忽略,在变幅载荷等塑性实际起明显作用的情况下,采用K的做法自然也就需要修正;作为改进, Nasgro关系式[12]考虑了塑性诱发的裂纹闭合效应,使得模型能够更好地描述疲劳裂纹扩展速率曲线的形状,但也使得速率模型的数学表达式更加复杂。
尽管如此,Paris关系式、Walker关系式、Nasgro关系式的共同特点都是将名义断裂力学参数作为裂纹扩展速率公式中的自变量,并基于力学参数对试验数据进行唯象拟合;而所有材料特征、裂纹几何形貌特征等引起的速率变化,统统归结到拟合参数中。在许多力学研究者撰写的教科书中,这些拟合参数被称为“材料参数”。
但是,这里不妨以Paris关系式为例来说明,将拟合参数(C和m)认为是材料参数的做法是不充分的。考虑给定宏观均匀各向同性材料的标准裂纹扩展试件,在给定载荷循环下进行裂纹扩展试验获得速率数据。
(1)从da/dN—ΔK曲线的形状出发,若选取不同的试验点速率范围,将获得不同的C和m拟合取值。
(2)裂纹扩展过程中,裂纹路径并不总是最理想的I型裂纹扩展路径,细观上会表现出“之”字形曲折前进,宏观上也有可能偏离一定的角度,这些都会引起裂尖场的变化,从而导致ΔK的计算误差;试验标准[13]中认为小于15°的数据都是可以接受的。
(3)采用不同厚度和类型的疲劳裂纹扩展试样,获得的疲劳裂纹扩展速率试验数据存在一定差别。
(4)疲劳裂纹扩展速率试验数据具有一定的分散性,这种分散性很大程度上来源于材料細观上的不均匀性和各向异性,也包括晶界和晶内扩展机制的不同影响,而作为“材料参数”的C和m却不足以反映这些影响。
综上,拟合参数既不是纯粹的材料参数,也不能比较精细地刻画材料对裂纹扩展的影响。对于传统工艺来说,宏观均匀各向同性的材料特点一定程度上掩盖了上述几个方面的不足,因此能够实现可接受的适用性;而对于新工艺新材料来说,其显著呈现出宏观尺度不均匀性与各向异性的特点,突破了现有模型的适用范围,因此效果较差。
总的来说,疲劳裂纹扩展应是力学因素和材料因素交互作用的结果。当前,疲劳裂纹扩展分析方法秉承“力学优先”的逻辑思路,对材料因素影响的考虑比较粗糙,对于力学因素和材料因素交互作用的认识和拆解也不够深入;反过来说,传统金属材料宏观均匀各向同性的特点既支持了当前分析方法的有效性,也限制了当前分析方法的适用性。
因此,无论对传统工艺金属材料还是对先进工艺金属材料,疲劳裂纹扩展分析方法都需要更深入地认识并表征力学因素与材料因素在疲劳机理中的交互作用,尤其是材料因素对金属疲劳裂纹扩展的影响规律。
2.2疲劳裂纹扩展研究的典型方向
近年来,关于疲劳裂纹扩展的研究大致分为对力学因素的考虑和对材料因素的考虑两类。
一方面,关注力学参数的研究,致力于寻找更合适的力学参数来代替应力强度因子K,最常见的替代参数是尖张开位移(CTOD)相关参数[14-17]。这类研究往往能够在裂纹闭合效应、载荷迟滞效应等方面得到更好的结果,但是所得参数的测量或计算比较复杂,甚至对CTOD的定义都不一致,难以用于评价方法。此外,这些参数仍是纯力学参数,不涉及对材料因素的考虑,对于先进工艺金属材料的适用性还有待研究。
在力学因素的研究方面,Hosseini等[18]的工作尤其值得注意。研究者将疲劳裂纹扩展看作裂尖小范围材料连续不断的失效过程,并能够由疲劳寿命数据预测,而不必通过试验来测定Paris关系式中的拟合参数。这更加说明了拟合参数的取值具有很强的力学依据,而不只是一个材料参数。该工作的另一个特点在于采用了数值模拟手段进行研究,对传统基于试验理论分析的宏观疲劳裂纹扩展研究形成有力补充。
另一方面,越来越多的力学工作者在研究后得到结论,即疲劳裂纹扩展受到力学因素和材料因素交互作用的影响,并进而投入到微细观尺度材料组织的研究中,基于材料学理论的方法由此得到重视。其中,具有代表性的方法包括晶体塑性有限元法和相场法等。然而,这些研究主要面向微细观尺度材料层面的变形/失效机理,所得结论还不足以直接服务于面向宏观尺度结构层面的疲劳裂纹扩展分析方法,同时可能仅适用于某种特定材料而不具备普适性。
然而,对于一些金属材料来说,材料因素的影响已不限于微细观尺度,而是能够在宏观尺度表现得十分显著。对于这种特殊情况,当前疲劳裂纹扩展分析方法难以解释其机理,基于材料学理论的方法限于尺度又难以直接应用,同时还缺乏能够将二者有效联系起来的跨尺度方法,因此疲劳裂纹扩展分析或损伤容限性能评估成为一项挑战。
综上,尽管研究人员已经公认了疲劳裂纹扩展是一个力学因素与材料因素交互作用的过程,但这句话更多地停留在各文献的结论中,还没有成为研究者看待、解决疲劳裂纹扩展问题的新视角、新武器。
3分析评价方法,建立思路
本部分内容主要以1.1节激光熔化沉积TC18钛合金为例,针对疲劳裂纹扩展问题中材料因素的影响(或力学因素与材料因素的交互作用),对其考虑方式及逻辑思路进行讨论。
3.1疲劳裂纹扩展路径偏折预测方法
对于疲劳裂纹路径偏折角度的预测,目前已经提出了若干种基于裂尖场的准则,如最大周向应力准则、最大拉应变准则、最大径向切应力准则、应变能密度因子极小值准则、等应变能密度线上的最大周向应力准则、最小J2准则等。这些准则都有各自的依据,但也都存在适用性的限制。
这里首先给出一个激光熔化沉积TC18钛合金疲劳裂纹扩展的例子进行说明,如图11所示。图中,由DIC法测出的裂尖变形场几乎是对称的,因此上述准则预测出的裂纹路径都是平直的(即应当以接近I型模式扩展),而实际裂纹路径却与平直方向呈38.4°的大角度偏折。该现象显著地偏离了上述多种准则的预测结果。

对于式(2),当力学因素发生变化时,不等式左侧的力学参数X发生变化;当材料因素发生变化时,不等式右侧的临界值XC发生变化。激光熔化沉积TC18钛合金疲劳裂纹路径偏折的根本原因在于材料因素呈现出不均匀性和各向异性,因此应当考虑对不等式右侧的临界值XC进行修正。上述准则都是根据变形场选取各种力学参数,实际上是对不等式左侧的力学参数X进行修正,自然无法对由临界值XC导致的现象进行较好的解释。
此外,疲劳裂纹路径偏折还将引起疲劳裂纹扩展速率的变化。Suresh[19]通过推导得出,偏折裂纹的应力强度因子小于同样投影长度平直裂纹,而裂纹扩展驱动力的减小将使疲劳裂纹扩展速率降低。因此,Suresh认为可通过引导疲劳裂纹路径偏折来降低疲劳裂纹扩展速率,进而延长疲劳裂纹扩展寿命。但是,Suresh的结论并不完全符合试验观测结果:在激光熔化沉积TC18钛合金疲劳裂纹扩展试验中,裂纹偏折处的速率既可能加快也可能降低,且以加快居多。
实际上,Suresh的理论推导本身没有问题,但却忽略了一个关键要点,即疲劳裂纹路径为什么会偏折?实际上,在载荷施加与试件几何都满足对称条件的情况下,疲劳裂纹路径发生偏折必然是由材料组织特征导致的,即偏折方向上的材料对疲劳裂纹的抗力更弱,而更弱的抗力就意味着更快的疲劳裂纹扩展速率。因此,最终的疲劳裂纹扩展速率应是由裂纹驱动力减小导致的速率降低和由材料抗力较弱导致的速率加快之间博弈妥协的结果,既有可能加快,也有可能降低,不能单独从其中某一个角度直接推理得到结论。
综上所述,当前的疲劳裂纹扩展分析方法仅从力学角度出发,没有考虑材料组织不均匀性和各向异性的影响。然而,疲劳裂纹扩展是力学因素和材料因素交互作用的结果,仅考虑纯力学参数的做法导致各种参数和准则只能作为疲劳裂纹扩展的表征,而无法揭示或体现疲劳裂纹扩展的根本原因。因此,当前的疲劳裂纹扩展分析方法仅适用于宏观均匀各向同性的传统工艺金属材料,不太适用于材料组织呈现显著不均匀性和各向异性的情况。
3.2“净驱动力”概念模型
基于上述分析,笔者提出了一个“净驱动力”的概念模型来说明力学因素和材料因素之间的关系[20]。仍以激光熔化沉积TC18钛合金疲劳裂纹扩展为例,其示意图如图12所示。在该模型中,应力强度因子或其他由裂尖场变形导出的名义断裂力学参数是裂纹扩展的驱动力,材料对裂纹扩展的抗力是裂纹扩展的阻力,而实际的疲劳裂纹扩展行为取决于“净驱动力”,可抽象地表述为“名义驱动力减去阻力”。
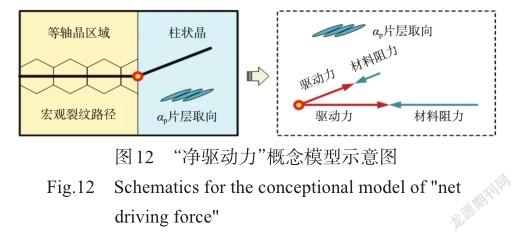
“净驱动力”的概念模型能够解释疲劳裂纹路径的偏折。对于上述塑性异性金属材料,虽然沿I型裂纹路径上的驱动力最大,但沿相界或晶界方向的阻力最小,因此净驱动力最小的方向应介于这两个方向之间(也包括这两个方向在内),而具体的偏折角度则取决于驱动力和阻力的相对大小。
“净驱动力”的概念模型也能够解释疲劳裂纹扩展速率的变化。疲劳裂纹既然发生偏折,说明偏折路径上的净驱动力比I型路径上更大,因此在发生路径偏折的一瞬间,其速率加快;但当裂纹路径偏折之后,路径偏折使得裂纹扩展驱动力下降,导致这一时刻的速率降低。因此,对于由材料因素引起的疲劳裂纹偏折来说,其速率最终是升是降和升降程度取决于名义驱动力和阻力的相对大小。
基于“净驱动力”概念模型重新审视线弹性断裂力学在疲劳裂纹扩展中的应用,可以发现均匀各向同性的材料假设实际上是假设各點各方向的阻力相同,这样一来净驱动力几乎完全由驱动力决定(可类比大气压的作用),导致路径在宏观尺度上符合I型模式。因此,经典断裂力学只需重点关注驱动力,便可在宏观尺度上较好地适用于大部分传统工艺金属材料。因此,当尺度逐渐趋于微观,当塑性影响越来越显著,当材料特征突破了均匀性和各向同性,经典断裂力学将越来越难以预测实际情况。
因此,从净驱动力的角度来看,应着重考虑材料裂纹扩展阻力的力学表征方法并建立疲劳裂纹扩展模型。而从第1节中的特殊现象以及其他相关文献报道来看,应当特别注重相界、晶界等材料界面的作用,以及材料塑性与疲劳性能之间的关系。此外,由于材料因素是一个局部的影响,其在宏观尺度上的影响将表现为分散性,因此适合采用概率统计的方法对其进行描述,而在微细观尺度的影响则适合采用数值模拟仿真的手段进行研究。
总而言之,应当从“力学因素与材料因素交互作用”的角度来看待疲劳裂纹扩展问题,其关键在于发展材料因素的宏观力学表征方法,而净驱动力概念模型则是该思路的一个合理可行的尝试。
4结论
本文针对材料因素对金属材料疲劳裂纹扩展的影响,对当前方法的逻辑思路进行分析讨论,并基于课题组近年试验工作中发现的疲劳裂纹扩展行为,从力学因素与材料因素交互作用的角度提出了“净驱动力”概念模型,得到了以下结论。
(1)当前疲劳裂纹扩展分析方法仅注重力学参数,也致力于寻找更合适的纯力学参数,材料因素的影响仅考虑了试验数据拟合参数,没有体现出疲劳裂纹扩展是一个力学因素与材料因素交互作用的过程。
(2)目前的一些新型金属材料,尤其是用于增材制造等先进工艺制造的金属材料,其材料组织呈现明显的不均匀性和各向异性,将导致其疲劳裂纹扩展发生路径偏折、路径分叉、速率波动等特殊行为。
(3)堅持“力学优先”思路的分析方法能够较好地适用于宏观均匀各向同性的金属材料,但难以解释或预测宏观上呈明显不均匀性和各向异性的金属材料中的特殊疲劳裂纹扩展行为。
(4)疲劳裂纹扩展是一个力学因素和材料因素交互作用的过程,可将名义断裂力学参数看作裂纹扩展的驱动力,将材料对裂纹扩展的抗力看作裂纹扩展的阻力,实际的疲劳裂纹扩展行为取决于“净驱动力”。
参考文献
[1]王向明.飞机新概念结构设计与工程应用[J].航空科学技术, 2020, 31(4):1-7. WangXiangming.Newconceptstructuredesignand engineering application of aircraft[J]. Aeronautical Science & Technology, 2020, 31(4): 1-7.(in Chinese)
[2]李鹏,潘凯,刘小川.美国空军机体数字孪生计划的回顾与启示[J].航空科学技术, 2020, 31(9):10. LiPeng,PanKai,LiuXiaochuan.Retrospectand enlightenment of the AFRL airframe digital twin program[J]. Aeronautical Science & Technology, 2020, 31(9): 1-10.(in Chinese)
[3]Wang K,Bao R,Jiang B,et al. Effect of primaryαphase on the fatigue crack path of laser melting deposited Ti-5Al-5Mo-5V-1Cr-1Fe nearβtitanium alloy[J]. International Journal of Fatigue,2018,116:535-542.
[4]Wang K,Bao R,Zhang T,et al. Fatigue crack branching in laser melting deposited Ti-55511 alloy[J]. International Journal of Fatigue,2019,124:217-226.
[5]Zhang T,Bao R,Fei B J. Load effects on macroscopic scale fatigue crack growth path in 2324-T39 aluminum alloy thin plates[J]. International Journal of Fatigue,2014,58:193-201.
[6]Zhang T,Bao R,Lu S S,et al. Investigation of fatigue crack propagation mechanisms of branching crack in 2324-T39 aluminum alloy thin plates under cyclic loading spectrum[J]. International Journal of Fatigue,2016,82:602-615.
[7]Bao R,Zhang X. Fatigue crack growth behavior and life prediction for 2324-T39 and 7050-T7451 aluminum alloys under truncated load spectra[J]. International Journal of Fatigue,2010,32:1180-1189.
[8]Nizery E,Ehrstr?m J C,Delgrange G,et al. A specimen to evaluate susceptibility of aluminum alloys to L-S crack deviation[C]// ICAF 2019-Structural Integrity in the Age of Additive Manufacturing:Proceedings of the 30th Symposium of the International Committee on Aeronautical Fatigue,2020:349-359.
[9]Joyce M R,Starink M J,Sinclair I. Assessment of mixed mode loading on macroscopic fatigue crack paths in thick sectionAl-Cu-Li alloy plate[J]. Materials & Design,2016,93:379-387.
[10]Fourmeau M,Marioara C D,B?rvik T,et al. A study of the in‐fluence of precipitate-free zones on the strain localization and failure of the aluminum alloy AA7075-T651[J]. Philosophical Magazine,2015,95(28-30):3278-3304.
[11]Walker E K. The effect of stress ratio during crack propagation and fatigue for 2024-T3 and 7075-T6 aluminum[C]// ASTM STP 462:Effects of Environment and Complex Load History on Fatigue Life. American Society for Testing and Materials,1970.
[12]NASGRO 8.1,Reference Manual(Version 8.1):Fracture mechanics and fatigue crack growth analysis software[R]. USA:NASA Johnson Space Center and Southeast Research Institute,2016.
[13]American Society for the Testing of Materials. ASTM E647-15:standard method for measurement of fatigue crack growth rates[S]. USA:American Society for the Testing of Materials,2015.
[14]Zhang W,Cai L,Zhou D Q,et al. In-situ microscopy testing of plasticity variation ahead of fatigue crack tip in AL2024-T3[J]. International Journal of Fracture,2019,216(1):59-70.
[15]Antunes F V,Serrano S,Branco R,et al. Fatigue crack growth in the 2050-T8 aluminum alloy[J]. International Journal of Fatigue,2018,115:79-88.
[16]Antunes F V,Branco R,Prates P A,et al. Fatigue crack growth modelling based on CTOD for the 7050-T6 alloy[J]. Fatigue & Fracture of Engineering Materials & Structures,2017,40(8):1309-1320.
[17]Antunes F V,Branco R,Prates P,et al. Fatigue crack growth versus plastic CTOD in the 304L stainless steel[J]. Engineering Fracture Mechanics,2019,214:487-503.
[18]Hosseini Z S,Mohsen D,Somerday B P,et al. On the theoretical modeling of fatigue crack growth[J]. Journal of the Mechanics & Physics of Solids,2018,121:341-362.
[19]Suresh S. Fatigue of materials[M]. New Jersey:Wiley Blackwell,1991.
[20]Liu B C,Wang K,Bao R,et al. The effects ofα/βphase interfacesonfatiguecrackdeflectionsinadditively manufactured titanium alloy:a peridynamic study[J]. International Journal of Fatigue,2020,137:105622.
Impacts of Material Factors on Metal Fatigue Crack Growth
Liu Binchao,Wang Qiuyi,Yang Rong,Lu Songsong,Bao Rui
Beihang University,Beijing 100191,China
Abstract: Developments of advanced processing and materials is violating the assumption of material homogeneity and material isotropy in classical fracture mechanics, and it is thus infeasible for the present analysis methods of fatigue crack growth (FCG) to apply, in which mechanical parameters are the focus and material impacts are considered merely as fitting parameters of experiment data. In this paper, typical fatigue crack growth behaviors are firstly introduced and the underlying mechanisms are briefly summarized, which are based on our relevant studies in the past few years. Then, the logics of present models and methods are analyzed, which implies that the research focus should be put on the reasonable and effective considerations of interactions between mechanical factors and material factors. Finally, prediction methods of fatigue crack path deflections are discussed, based on which a conceptional model of net driving force for FCG is proposed. The analysis and discussions in this paper help conceive FCG from the perspective of mechanics-material interaction, and the obtained conclusions can provide guidelines for FCG analysis of advanced materials as well as damage tolerance evaluations of corresponding structures.
Key Words: fatigue crack growth; crack deflection; crack branching; material texture; additive manufacturing

