基于改进Elman模型的电信公司客户流失分析

曹 宁，王雨薇，高 莹，徐根祺，任小文

(1.西安交通工程学院 土木工程学院，西安 710300；2.西京学院 土木工程学院，西安 710123；3.西安交通工程学院 电气工程学院，西安 710300)

近几十年以来，随着科学技术的迅猛发展，服务行业(如电信、银行、酒店、汽车等)的产业市场格局发生了地覆天翻的变化，各大公司对客户的竞争亦愈演愈烈，客户流失成为了每个公司关注的焦点[1]．企业家们也已经将减少老客户流失作为公司的首要目标[2]．客户流失指某企业现有的客户终止继续购买其商品或服务，转而购买其竞争对手的商品或服务[3]．在当下的商业竞争环境中，获得新客户的成本非常高，远不如维持好老客户所能够获得的收益[4]．目前，电信公司的客户流失率非常髙，有研究表明降低客户流失率可以显著增加公司利润[5]．因此，分析客户流失的趋势就显得尤为重要．

目前的研究在预测客户流失方面取得了较大的成就．客户流失分析研究方法的选择、数据不平衡等问题均得到了有效解决．学者们将客户流失分析作为一种分类问题来研究，于是，有监督的学习算法被大量地应用于客户流失分析，且取得了较好的效果．根据使用方法的不同，客户流失分析的研究方法主要包括统计学[6]、人工智能[7]、集成学习[8]和社会网络分析[9]．但是，以上方法使得人们不得不在特征处理上花费大量的时间和精力，且预测效果也并非总是令人满意[2]．

为了获取更加准确的预测结果，本文将灰色系统和Elman神经网络[10]相结合，提出一种新的电信公司客户流失分析模型．首先采用传统的单一GM(1，1)模型来挖掘客户流失的规律，但是该方法在预测精度方面有所欠缺，与实际客户流失的趋势拟合度不高．而Elman 神经网络的预测精度高、误差小，对非线性波动的跟踪预测的能力强，现已在工农商等多个领域得到广泛应用．因此,将GM(1，1)和Elman神经网络结合，能较大地提高客户流失的预测效果．

1 相关理论

1.1 灰色理论

在海量数据的背后，必定蕴含某种特定规律，生成的灰数能够帮助我们获得信息，揭示出这些规律，这就是著名的灰色系统理论．GM(1，1)为灰色理论模型的典型模型，被众多研究者们应用于不同的领域且均表现不俗．为了寻找预测所需的信息，需要在建模时对初始数据进行处理，去掉不合理的部分，使系统误差尽可能地减小，以此改善预测准确度．GM(1，1)建模过程如下：

设原始数据为

X(0)=(X(0)(1)，X(0)(2)，…，X(0)(n))

(1)

对X(0)进行累加，得到新序列：

X(1)(t)=(X(1)(1)，X(1)(2)，…，X(1)(n))

(2)

利用最小二乘法估计参数：

(3)

对得到的新序列求导，可得GM(1，1)模型的公式：

(4)

对上式依次累减可到预测值．

(5)

令预测值与实际值之差为残差，记为ε(0)(t)．

使用GM(1，1)模型预测客户流失的趋势，然而仅用单一GM(1，1)模型进行预测会导致较大的误差，故为了提高模型的精度，采用Elman算法对残差进行修正．

1.2 Elman神经网络

Elman神经网络属于经典的局部回归神经网络．Elman神经网络在网络结构上比前向神经网络多一个反馈层，因此对历史数据比较敏感．Elman神经网络共由四层组成，分别为输入层、反馈层、隐层和输出层，其中反馈层与隐层的神经元数目相同．输入层神经元用于数据序列的传输，反馈层可记忆隐层节点前一时刻的输出并返回网络输入，隐层的传递函数一般选择Sigmoid函数，输出层对处理结果进行线性加权．通过Elman神经网络模型能够较好地拟合多种因素对客户流失的影响，从而作出准确预测．图1为Elman神经网络结构图．

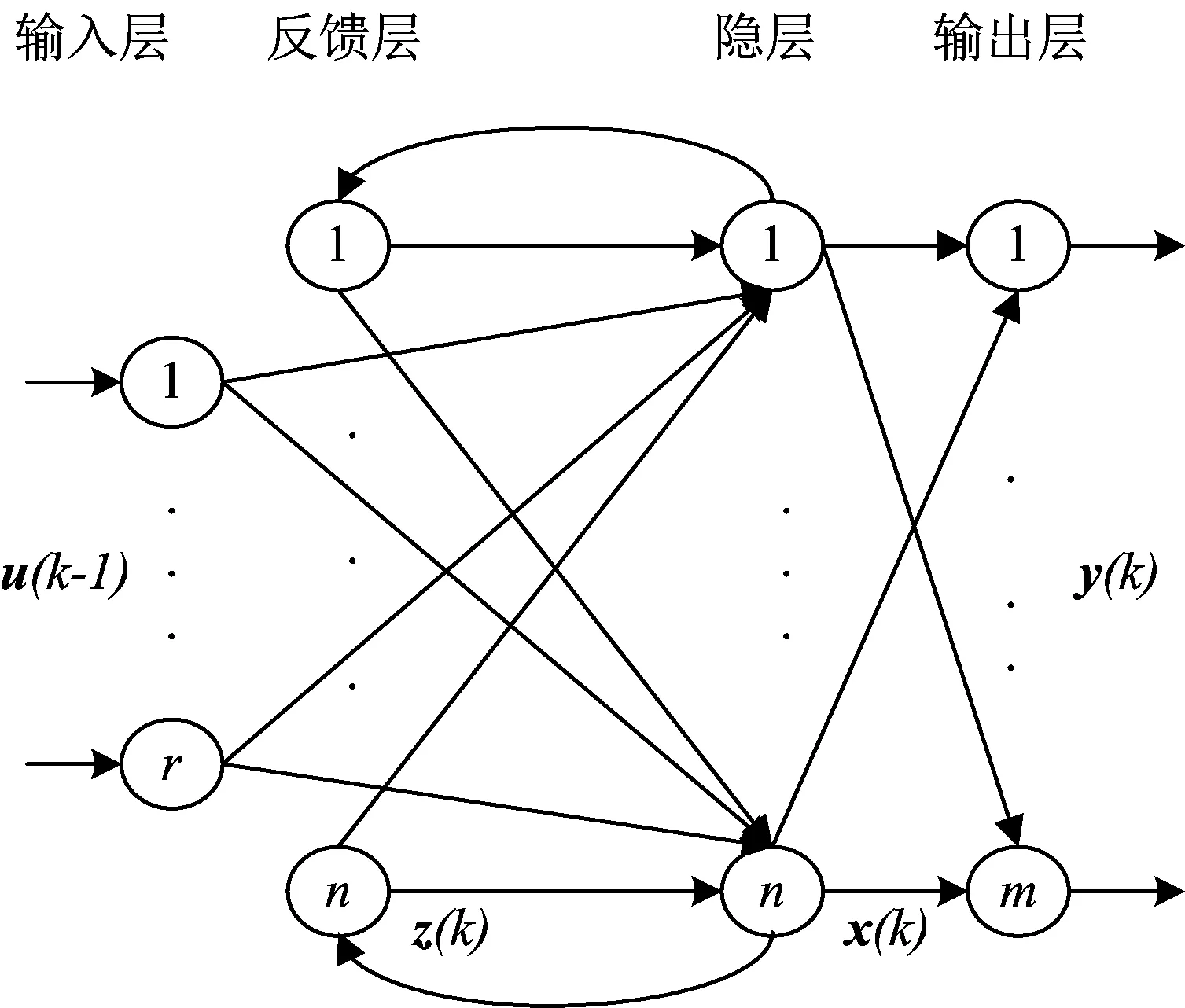
图1 Elman神经网络结构图

在k时刻的Elman神经网络可以描述为：

y(k)=g(ω1·x(k))

(6)

x(k)=f(ω3·z(k)+ω2·u(k-1))

(7)

z(k)=x(k-1)

(8)

其中，u为输入向量(u∈Rr)；y为网络输出向量(y∈Rm);x为隐层输出向量(x∈Rn)；z为状态反馈向量(z∈Rn)；g(·)为输出层传递函数，f(·)为隐层传递函数；ω1分别为隐层至输出层的连接权值；ω2为反馈层至隐层的连接权值；ω3为输出层至隐层的连接权值．

用误差平方和函数作为Elman神经网络的指标函数，表达式如下：

(9)

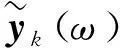
构建Elman 预测模型步骤如下：

(1)构建网络，初始化模型，为每一层参数赋值；

(2)选择训练模式，依据实际情况键入输入和输出方法；

(3)建立输入方式后，从最初的隐层开始计算每个神经网络的输出；

(4)从输出层反向到第一隐层，修改每一个单元的连接权值．通过多次修正，最终得到理想的输出结果；

(5)重复步骤(2)和(3)，直至所有的样本数据都被录入且输出预测值时停止．

数学模型如下：

传递函数：f(x)=(1+e-x)-1

最终根据反向传播，得到误差平方和的最小值，修正公式为：

Δωi(1+j)(k+1)=(1-mc)η(tk-yk)g′(·)xj(k)+mcΔωi(1+j)(k)

(10)

1.3 修正残差

(1)将拟合生成的数据残差作为Elman动态神经网络模型的输入，同时作为模型样本进行训练．

(2)训练完成后，利用多步循环预测法对残差进行调整、预测．

(3)最后，将灰色模型预测值和通过Elman模型对残差修正后的预测值相加得到最终数值．

1.4 客户属性选择

根据OSA算法基本原理，设有m个客户属性，用W表示客户数据样本空间，对W进行直和分解，分解为样本容量相等的A和B，即W=A⨁B且A=B．由于电信公司客户的数据相当庞大，不会对结论产生影响．A和B的客户数据的长度为L．

P={1，2，…，m}，Q={1，2，…，L}

(11)

对第i个客户数据变量，利用最小二乘法在客户数据样本空间W上进行客户数据参数估计，有

xi=a0+bx0，i∈P

(12)

采用最小二乘法对A和B进行参数估计，有

(13)

计算客户数据的最小偏差准则值

(14)

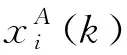
对于xi，xj，…，xp，xr，i，j，…，r∈P，在样本空间A和B上根据最小二乘法估计参数，有

设客户数据最小偏差准则为bestη=η*h，bestη相应方程组变量为特征变量．这些特征变量所对应的属性变量，就是根据OSA选取的客户属性．

1.5 评价指标

(1)通常都是以误差形式对预测结果进行估计，但单一的指标往往并不科学也不可靠，因此本研究使用均方误差(MSE)和均方根误差(RMSE)两种指标对模型的性能进行评价，定义如下：

(2)这里采用精准率(precision)、准确率(accuracy)，F1值(F1)和召回率(recall)作为模型评判的主要指标，如下所示：

(15)

(16)

(17)

(18)

以上式子中，TP表示正确预测流失客户的样本个数；TN表示正确预测非流失客户的样本个数；FP表示错误预测流失客户的样本个数；FN表示错误预测非流失客户的样本数．

2 客户流失分析模型建立

(1)通过各种渠道收集客户行为数据，确定初始属性集合；

标准化等预处理过程．本研究选取A电信公司2018年1月至2020年6月的客户数据作为初始数据，采用如下标准化方法来剔除多因素间由于量纲不同而产生的差异：

X=x-xmin/xmax-xmin

(3)基于OSA算法对客户关键属性进行选取．

(4)将准备好的数据集输入GM(1，1)模型，预测出人员流失变动的趋势，再通过Elman模型对残差进行修正，得出最终客户流失情况．

模型结构如图2所示，分析流程如图3所示．

图2 GM-Elman客户流失分析模型

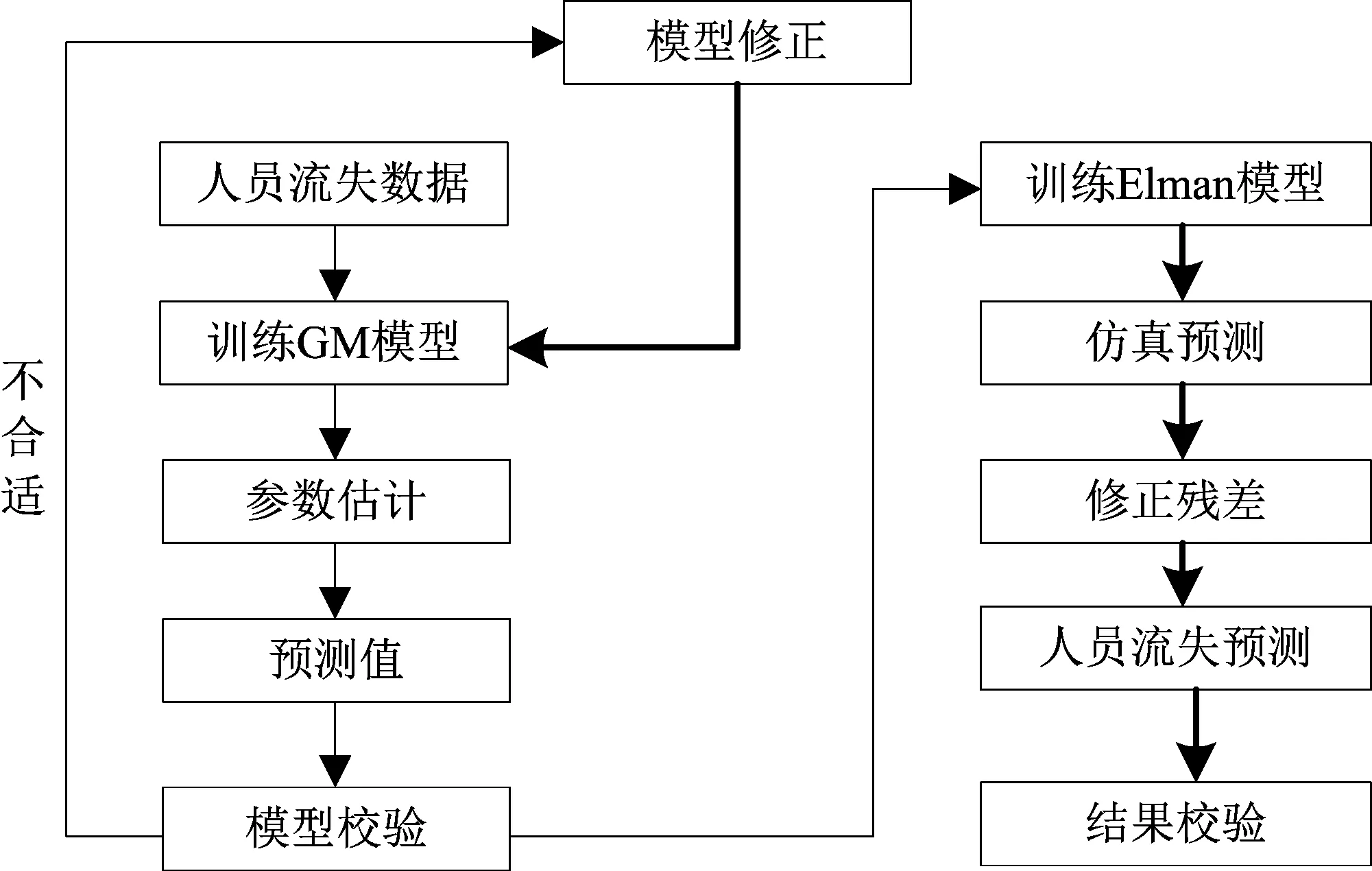
图3 GM-Elman客户流失分析流程图

3 实验分析

根据所选取的数据进行客户流失情况的分析，将本研究中所用模型与遗传算法优化的BP神经网络(GA-BP)模型、支持向量机(SVM)模型以及卷积神经网络(CNN)模型的结果进行对比，各模型的误差如图4所示．

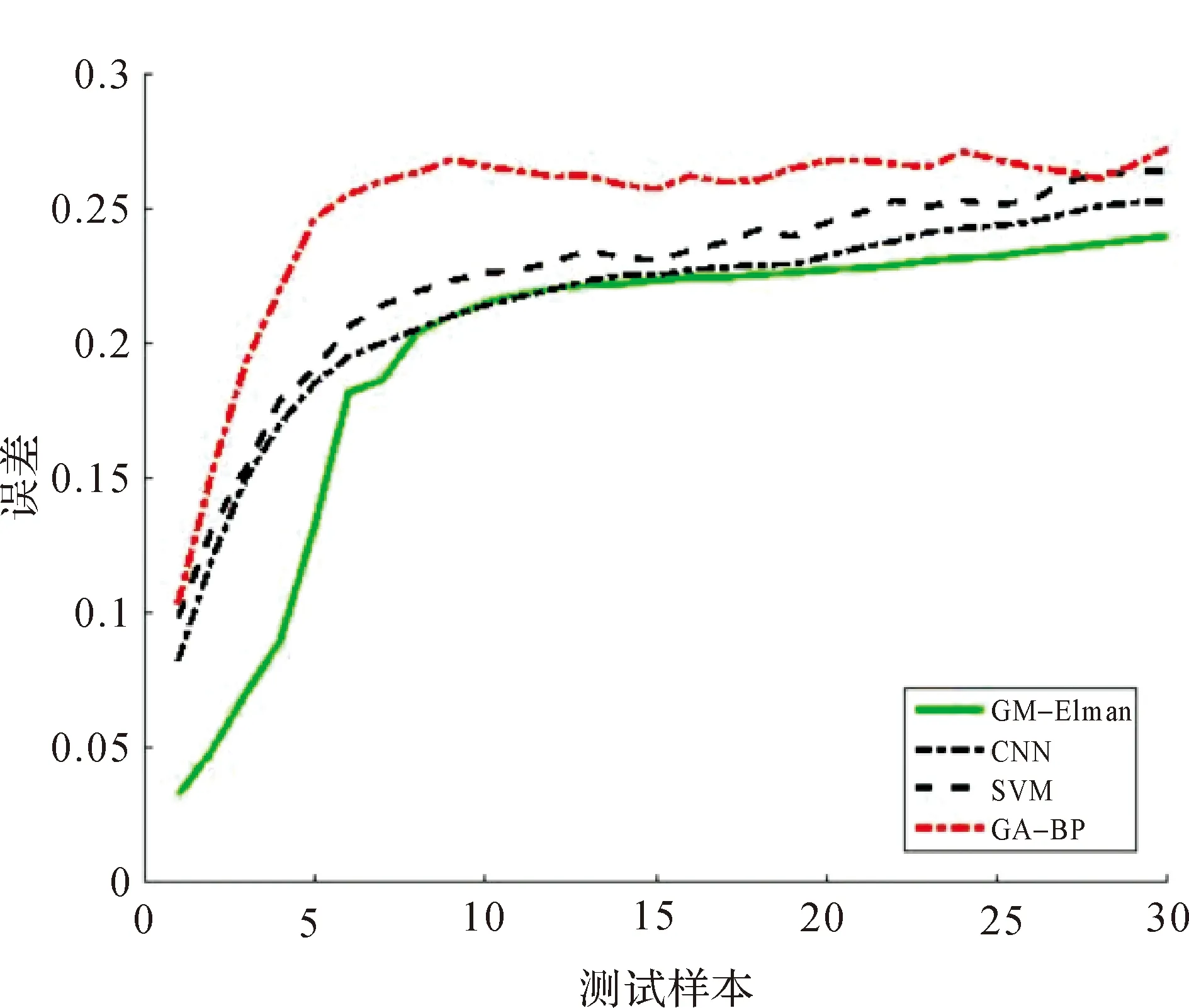
图4 四种模型误差对比图

图4表明，在四种模型的误差比较中，GM-Elman的误差明显低于其它模型的误差，采用GM(1，1)与Elman神经网络相结合方法的结果要比实际客户流失的变动曲线更加拟合．利用均方误差根误差(RMSE)和均方误差(MSE)两个指标进行衡量并对比分析，由表1可以看出，GM-Elman模型的预测结果相对应的RMSE和MSE均为最小，同时相对于其它三种模型可靠性也最高．

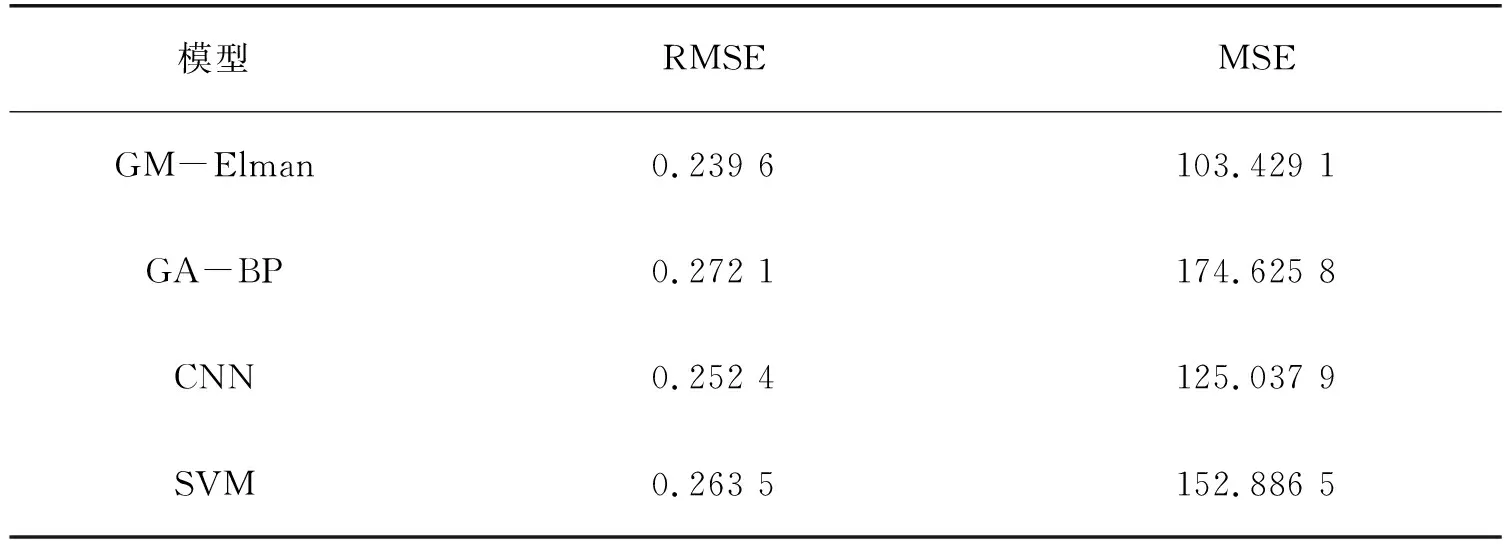
表1 四种模型的RMSE和MSE数值表

为了比较直观地分析各模型的性能，本节对各模型的AUC值进行对比分析，具体数值如表2所示．

表2 各模型AUC值比较

从表2可以看出，通过AUC值对四种模型的测试样本进行对比，GA-BP、SVM及CNN的AUC值相对较低，一些样本的预测准确率较低，还有待提高．对比之下，改进后的GM-Elman神经网络的AUC值基本在0.90以上，且改进后的算法准确性更好，应用较好．

表3为各模型的实验结果，其结果显示改进后的GM-Elman神经网络的精准率为85.21%，F1值为77.33%，均比其它三种模型略高，而准确率为95.19%，比CNN、SVM和GA-BP分别高2.51%、3.58%和6.72，召回率为72.01%，分别高出CNN7.65%、SVM9.26%和GA-BP10.92%，该结果表明改进后的GM-Elman模型相比于其它三种模型能够更有效地对客户流失进行预测．

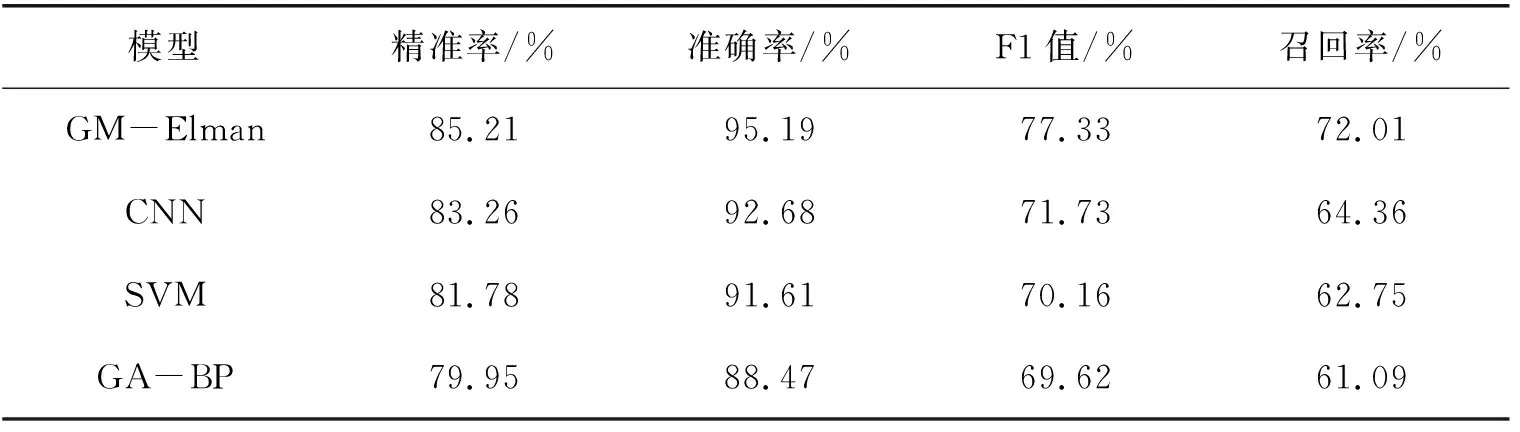
表3 四种模型实验结果

4 结论

通过对客户流失分析模型的深入研究，基于灰色系统对Elman神经网络进行了改进，提出了GM-Elman神经网络预测模型，并结合X电信公司的实际样本数据，分别和CNN模型、SVM模型及GA-BP模型进行了对比仿真验证，结果显示：GM-Elman预测模型在精准率、准确率、F1值和召回率方面均高于其它三种模型，该模型能够帮助企业准确分析客户流失的实际情况，为全面有效地开展客户关系管理提供更好的决策支持．