物理光学综合实验仪的制作及性能测试
韩飞宇,赵小侠,张云哲,于 阳,沈睿静,张 莎
(西安文理学院 机械与材料工程学院,西安 710065)
光和实物一样,是物质存在的一种形式,它同时具有波动性和粒子性.光具有波粒二象性,光作为一种极高频率的电磁波,频率高(可见光波段频率ν:7.5×1014~4.1×1014Hz)波长短(可见光波段波长λ:390~760 nm)是它区别于无线电波的最主要性质[1].因此光学发展史上Newton (1643—1727年)光的微粒学说和Huygens(1629—1695年) 光的波动学说才进行了近两个世纪的争论.波长短的特性导致它的波动性不明显,Thomas Young(1773—1829年)于1801年提出杨氏双缝实验,证明了双光束的干涉现象,并预言了光是横波.Fresnel(1788—1827年)完成了许多实验,论述和证实了光波具有干涉与衍射现象(泊松亮斑、菲涅耳圆孔衍射等).这样光的波动学说才无可辩驳的得到世人的接收.19世纪70年代Maxwell统一了电和磁的理论,建立了他著名的Maxwell方程组,预言了电磁波的存在,指出光是一种电磁波,其速度与电磁波相同.Hertz于1887年用实验产生和探测了电磁波,证实了Maxwell的电磁理论.这样光在电磁波谱中有了一席之位.1881年,迈克尔逊发明了迈克尔逊干涉仪(Michelson Interferometer),它是利用分振幅法产生双光束以实现干涉.通过调整该干涉仪,可以产生等厚干涉条纹,也可以产生等倾干涉条纹.由于相互干涉的两束光是分离的,后续的多数干涉仪都是在迈克尔逊干涉仪基础上的改进,因此迈克尔逊干涉仪在光学发展史上具有重要地位,该实验也是物理光学实验课的主要内容.目前物理光学实验室里有用来验证波的干涉、衍射和偏振性能的各种仪器.实验室的干涉仪能做等倾干涉,等厚干涉,劈尖实验,衍射仪可以做各种形状衍射物的菲涅尔衍射和夫琅禾费单缝衍射.而市场上所售的这三种实验仪器,都是分开销售,且价格偏高.本课题设想设计一种物理光学实验仪将上述三种实验仪整合光路,并对光路进行优化,在一个光学小平台上融合为一体.主要是通过分束镜的合理使用,将干涉、衍射和偏振三种光路在小尺寸实验台上实现.下面介绍我们设计和研制的物理光学实验仪,以及实验仪的性能测试.
1 物理光学综合实验仪的设计与制作
1.1 物理光学综合实验仪的设计前期准备
在查阅文献资料,充分熟悉干涉、衍射、偏振三种类型实验特点的基础上,确定了物理光学综合实验仪预期实现的实验种类及所需要器件型号及尺寸.通过多次理论推演,最后确定物理光学综合实验仪主要可以完成干涉、衍射、偏振三类实验,预期可完成的实验有:迈克尔逊干涉仪的调节、基于迈克尔逊干涉仪测量透明介质的折射率、基于迈克尔逊干涉仪劈尖干涉的验证、菲涅耳衍射、夫琅禾费衍射、光栅衍射、偏振光的产生与检验、马吕斯定律的验证等实验.
1.2 物理光学综合实验仪的基本光路设计
在前期理论推演的基础上,完成了物理光学综合实验仪的光路设计,其光学附件示意图如图1所示:
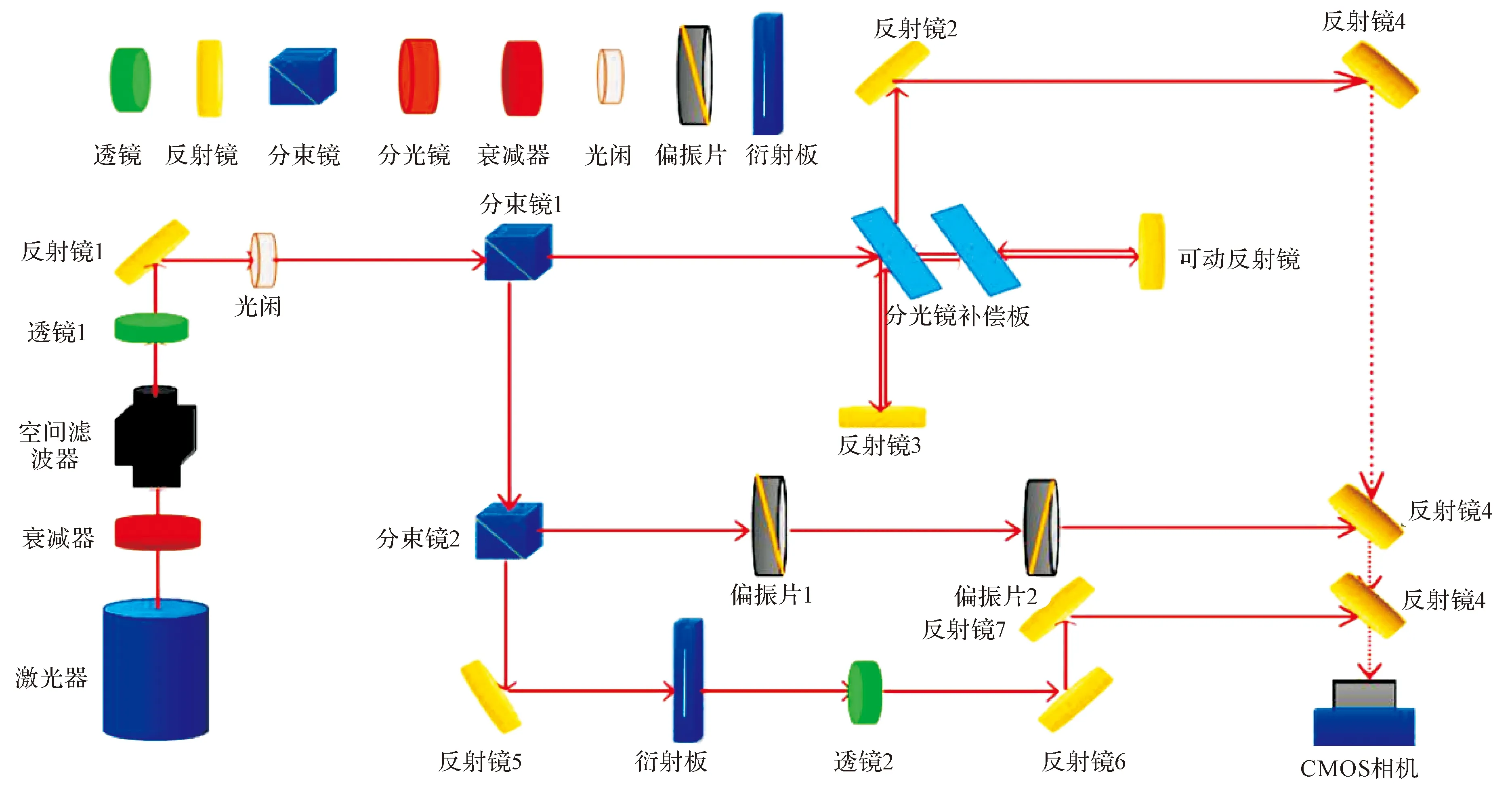
图1 物理光学综合实验仪光学附件布局参数示意图
其中主要器件包括:实验仪平台(亚克力板材质)、激光器、衰减器、空间滤波器、透镜1、反射镜1、光阑、分束镜1、分光镜、补偿版、反射镜2、反射镜3、可动反射镜、反射镜4、分束镜2、偏振片1、偏振片2、反射镜5、衍射板、透镜2、反射镜6、反射镜7、图像采集装置.
物理光学综合实验仪的设计光路中各个器件放置的距离参数如下:
主光路:激光器、衰减器、空间滤波器之间距离均为50 mm,空间滤波器与透镜1距离为100 mm,透镜1与反射镜1之间距离为 100 mm,反射镜1与光阑,光阑与分束镜之间距离分别为 20 mm和50 mm.
干涉光路:分束镜1距分光镜 70 mm,分光镜与补偿板之间距离为 40 mm,补偿板距可动反射镜160 mm,分光镜距反射镜2距离为100 mm,分光镜距反射镜3距离为200 mm,反射镜2与反射镜4距离 300 mm,反射镜4距 CMOS相机最远距离为400 mm.
偏振光路:分束镜2距偏振片1间距130 mm,偏振片1和2之间距离为 150 mm,偏振片2距反射镜4距离为90 mm,反射镜4距CMOS相机距离为150 mm.
衍射光路:反射镜5距衍射板间距离为140 mm,衍射板与透镜2 距离为80 mm,透镜2 与反射镜6距离为80 mm,反射镜6与反射镜7间距离为 75 mm,反射镜7与反射镜4 距离为70 mm,反射镜4距 CMOS相机75 mm.
1.3 物理光学综合实验仪的制作
根据上述设计的物理光学实验仪光路图,经过比较选定了合适的器件型号及尺寸,完成实验仪的制作,并进一步优化实验光路.其中衍射光路以带有刻度的小型轨道来固定各器件,以便于后期各实验的具体调试;反射镜4与CMOS相机之间固定一小型轨道,这样需要采集某路实验现象只需要将反射镜4移动至该路现象处,即可完成采集.制作完成后的物理光学综合实验仪如图2所示.

图2 物理光学综合实验仪实物图
2 物理光学实验仪的基本原理及测试结果
2.1 光的干涉实验
迈克尔逊干涉仪调制实验及基于迈克尔逊干涉仪测量透明介质(空气)折射率的实验光路图如图3所示.
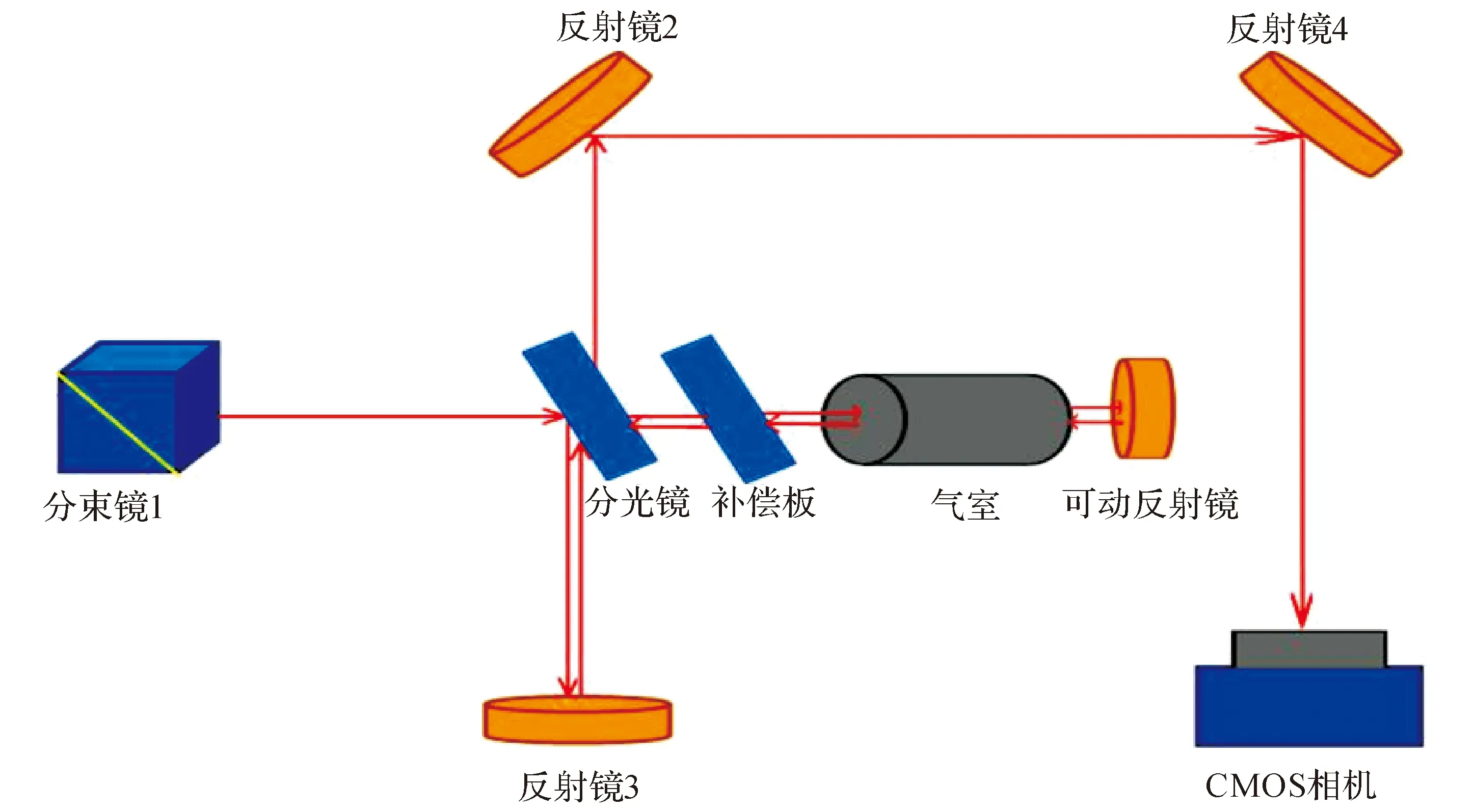
图3 迈克尔逊干涉实验光路示意图
迈克尔逊干涉仪基本光路:光束由分束镜1射出,经过分光镜一分为二路,第一光路经反射镜3反射后透过分光镜,经反射镜2和反射镜4反射射入CMOS相机;第二束光经过分光镜和补偿板透射后入射到可动反射镜上附带的反射镜,经反射镜反射后再次回到分光镜上,经分光镜反射后,同样经反射镜2和反射镜4反射射入CMOS相机.最终经分光镜反射和透射的二束光在其上侧空间形成一非定域的干涉场.在CMOS相机里干涉,CMOS相机经数据线与计算机相连接,这样可以在计算机屏幕上看到干涉条纹.屏上的干涉条纹可以看作反射镜反射出的两个虚光源发出的球面波干涉的结果.
通过调整迈克尔逊干涉仪基本光路中两个反射镜(反射镜3和可动反射镜)的相对位置,可以完成下面两种干涉实验.实验结果如图4所示:

图4 迈克尔逊基本光路实验结果图
第一种是实现等倾干涉:微调反射镜让两个反射镜保持完全垂直[2],此时为等倾干涉图样如图4(a)所示.
2d=kλk=1,2,… 明纹
(1)
2d=(2k+1)λ/2k=0,1,2,… 暗纹
(2)
式(1)和式(2)中的λ为所用激光器的波长,d为反射镜3和可动反射镜在分光镜中的像之间的距离,k为条纹的级次.
如果在补偿板后加上压强可调的气室或者折射率为n的透明介质材料,式(1)式(2)变为:
2(n-1)d=Δmλ
(3)
式(3)中d为透明介质的厚度或者气室的长度,n为一定压强下空气的折射率或透明介质的折射率,Δm为透明介质放入导致明(暗)条纹移动的个数.λ为所用激光器的波长.如果d、n和Δm已知的话同样可以用来测量待测激光器的波长.
第二种是实现等厚干涉:如果微调可动反射镜上的反射镜使得可动反射镜与反射镜3之间存在一个微小的夹角,此时两束反射光线将不再平行,从而产生等厚干涉,屏上出现如上图4(b)所示的弯线或接近直线的等厚干涉条纹.
迈克尔逊实验光路还可以完成牛顿环实验,在竖直放置的反射镜3表面放置一个曲率半径为R的平凸透镜,调整两个反射镜完全垂直,此时屏上出现一组如图4(c)所示的明暗相间的同心圆环,这些圆环是不等间距的,离圆心越远,圆环越密,且与等倾干涉圆环最主要的差别在于由于半波损失的存在牛顿环中心是暗环.
2.2 光的衍射实验
物理光学综合实验仪设计的衍射和偏振光路如图5所示:
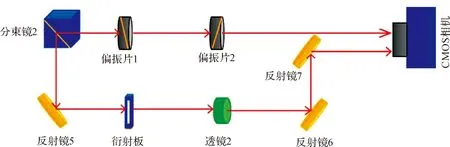
图5 衍射和偏振光路示意图
光的衍射是光在传播过程中遇到与自己波长可比拟的障碍物时出现的绕过障碍物在障碍物阴影区域传播的一种现象.光的衍射根据衍射物的不同可以分为单缝衍射、双缝衍射、圆孔衍射和光栅衍射等.
衍射光路:光束通过分束镜2后,到达反射镜5,经过反射镜5反射到达衍射板实验光路,衍射光路以带有刻度的小型轨道来固定各器件,方便完成各种实验,即根据需要对实验器件进行更换和距离调整.
下面以光的夫朗禾费衍射实验为例进行基本光路阐述:当光束通过反射镜5到达衍射实验光路后,通过调整衍射板上的圆孔位置使光线穿过圆孔到达透镜前焦点,最终在透镜后焦点放置反射镜6,并通过反射镜6、7将衍射图样传输至与计算机相连接的CMOS相机上,在计算机屏幕上观察到实验结果.
通过衍射光路完成的实验结果如图6所示:
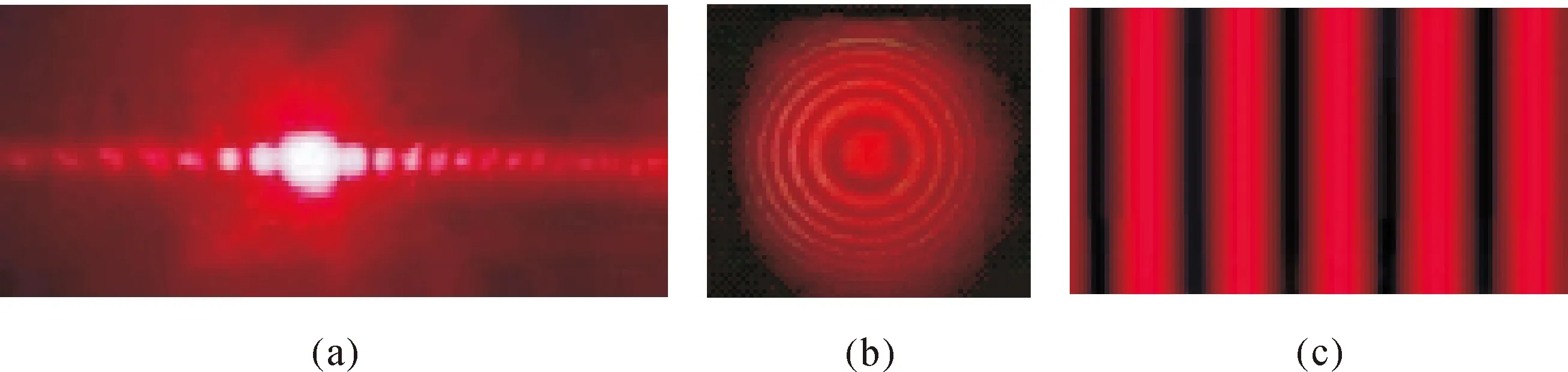
图6 衍射光路实验结果图
单缝衍射是研究光的波动性的重要实验.调整衍射光路使光源水平穿过单缝中心,此时屏上出现与狭缝方向平行的一系列如图6(a)所示的明暗相间的条纹,可以看出单缝衍射中央亮条纹宽度是其它级亮条纹的2倍,随着亮纹级次的增加,光强呈现减弱趋势[3].
若将衍射物替换为圆孔,经反射镜3反射的光水平穿过圆孔中心,此时CMOS相机上将接收到如图6(b)所示的圆孔衍射图样.
任何具有空间周期性的衍射屏都可以叫做衍射光栅.将衍射物替换为光栅,让反射镜3反射的光线水平通过光栅,此时屏上将出现一系列如图6(c)等宽等间距的平行狭缝.如果将衍射物替换为其他形状如六边形衍射、正方形衍射物可以得到相应的衍射图样.
2.3 光的偏振性的检验
光的偏振性是光的波动性的重要体现.只有横波才有偏振现象,因此光的偏振性实验也是光是横波的又一例证.本物理光学实验仪中光的偏振性实验光路已基本在图5体现,经分束镜射出的光束,经偏振片1(起偏器)、偏振片2(检偏器)射出后将相机CMOS位置处置换为功率计,实验中是通过调整偏振片1和2的位置及两偏振片透振方向间的夹角θ来完成实验的.而马吕斯定律的测量是研究光的偏振性的代表性实验.经分束镜射出的光束通过偏振片1变成光强为I0的线偏光,再垂直入射到另一块偏振片2上,出射光强为I=IOcos2θ,这就是马吕斯定律[3],其中θ为两偏振片透振方向之间的夹角.
3 物理光学实验仪的性能测试
使用制作好的物理光学综合实验仪进行了下面的实验验证,实验数据如下.
3.1 迈克尔逊干涉仪实验
利用迈克尔逊干涉实验光路及CMOS相机采集、分析软件测量空气折射率实验过程如下:
在图3所示的迈克尔逊干涉仪实验中,在其中一个光路中放入一个气室,然后通过充气改变空气的压强,这束光的光程会改变,干涉环的数目会发生变化[4].这时光程差由式(3)确定,因此
(4)
其中Δn为空气折射率随压强变化的变化値,λ为光源的波长,Δm为压强变化导致的干涉环溢出的个数.
空气折射率和空气的温度、压强有关[5-8],对于理想气体有:
(5)
其中n和ρ是空气在T温度和P压强下的折射率和密度,其中T为开尔文温度,P为mmHg,ρ0和N0是标况下空气的密度和折射率,T0为标况下的开尔文温度.所以有:
(6)
当温度恒定时,气压不太高时,气体折射率的变化Δn与气压的变化ΔP(气室充气前后的压强差)成正比,因此有:
(7)
与式(4)联立可得:
(8)
故可得空气折射率为:
(9)
室温下,压强为Ρ=760 mmHg,气室长度为L=10.00 cm时利用迈克尔逊干涉实验光路测量空气折射率的实验数据见表1.

表1 利用迈克尔逊干涉仪测量空气折射率的实验数据表
则测量得到的空气折射率为:
3.2 马吕斯定律验证
(1)保持起偏器(偏振片1)固定不动,旋转检偏器(偏振片2),观察功率计上光强的变化,当功率计上光强示数为零时固定检偏器位置,之后缓慢旋转检偏器,每旋转15°,记录下功率计的示数,并完成下表2.
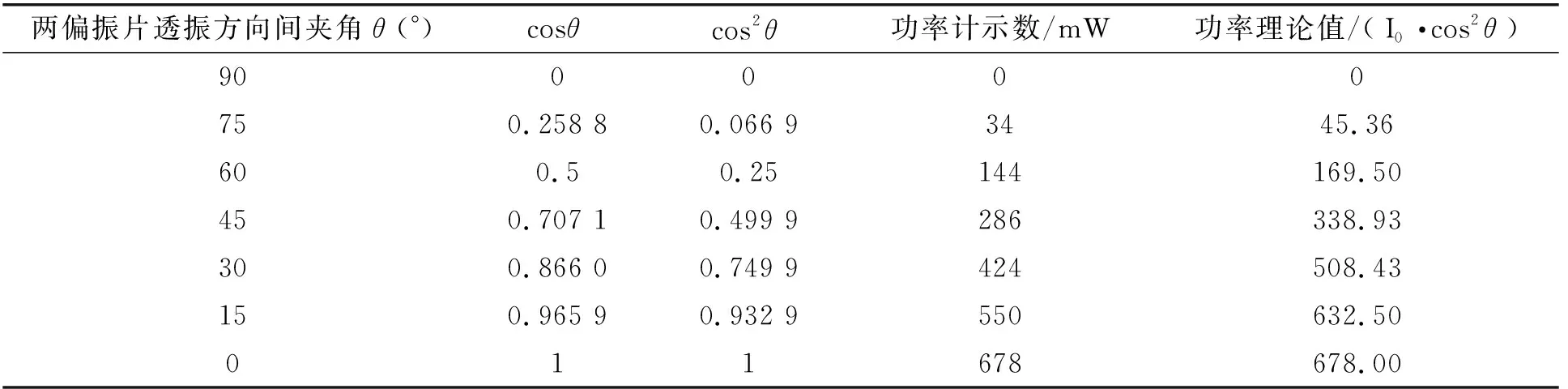
表2 马吕斯定律验证实验数据
(2)根据马吕斯定律和测量得到的数据绘制如图7所示的光强变化曲线.其中,横坐标为两偏振片透振方向间夹角(°),纵坐标为功率计所测的光强I(mw).
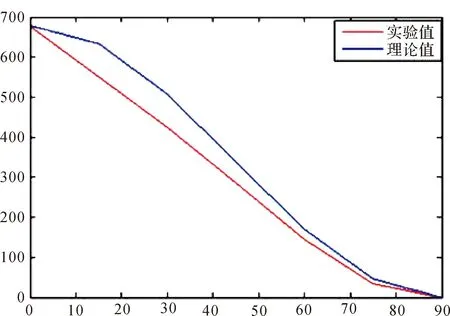
图7 马吕斯定律光强变化曲线图
4 结语
本文介绍了课题组设计的一款物理光学综合实验仪,对综合实验仪的光路进行了设计,并基于设计光路研制出一台物理光学综合实验仪,实验验证该物理光学实验仪满足物理光学实验的实验要求.这对于光学实验室在经费有限的前提下可以满足广大师生的实验要求,同时可以减少以前光学实验仪器多,且不同实验需要摆放实验仪器给实验人员造成频繁搬动麻烦的缺点,同时可以消除精密光学仪器搬动造成的仪器损坏的可能,为广大师生提供便利.同时减小学校对物理光学实验经费的投入,有利于学校将有限的经费用于新的实验仪器购置.

