竖直矩形通道内超临界正癸烷振荡特性的大涡模拟

李 勇，孙 丰，谢公南，曹 桢，傅佳宏

（1.西北工业大学航海学院，西安 710072；2.太原理工大学电气与动力工程学院，太原 030024；3.隆德大学能源科学系，隆德SE⁃ 22100；4.浙大城市学院机械电子工程学系，杭州 310015）

以碳氢燃料为推进剂的超燃冲压发动机被普遍认为是高超声速飞行器的核心部件［1］。超燃冲压发动机在高超声速下飞行时，燃烧释热和气动加热双重作用使得燃烧室的热负荷剧增，仅依靠被动隔热无法保证超燃冲压发动机在高飞行马赫数下运行的安全性［2］，采用自身燃料作为冷却剂的主动再生冷却技术被认为是解决燃烧室热管理的最有效途径之一［3⁃4］。由于燃烧室内压力一般在3.5～7.0 MPa 之间［5］，超过了碳氢燃料的临界压力2～3 MPa，因此，利用再生冷却通道内超临界碳氢燃料的对流传热过程以吸收燃烧室壁面热量，从而实现超燃冲压发动机燃烧室安全运行的目的。

研究人员对超临界碳氢燃料在矩形通道内的对流传热特性（传热恶化和传热强化）进行了大量的实验和数值研究。Zhu 等［6］认为浮升力有助于竖直向下流动工况下的传热性能，但对竖直向上流动工况则反之。Pu 等［7］观察到流道截面温度分布不均匀，同样认为浮升力在超临界流体流动传热过程中不能被忽略。Lei 等［8］和Li 等［9］指出相比于圆形通道，矩形通道内超临界碳氢燃料裂解转化率和热沉更具有优势。Hou 等［10］对比分析了碳氢燃料有无裂解反应条件下流体温度和壁面温度分布情况，发现裂解反应的化学吸热能力可有效提升碳氢燃料的冷却性能。张斌等［11］实验研究了热流密度和进口温度对国产航空煤油RP⁃3 传热特性的影响规律，认为竖直向上管和向下管进口处均会出现传热恶化现象。Li 等［12］数值研究了壁面导热系数对超临界正癸烷温度分布的影响规律。Sun 等［13］同样分析了壁面导热系数对热输运的影响，发现在较大导热系数工况下，浮升力诱导的二次流被极大地削弱。Hu 等［14］观察了不同工况下的二次流强度，认为较大的质量流率和运行压力降低了二次流强度，但体积热源密度起到相反的效果。程泽源等［15］研究了换热通道的直径大小对传热性能的影响规律，认为直径越大，传热恶化现象越容易发生。

针对超临界传热恶化现象，不同的强化换热方法被提出，Li 等［16］研究了不同螺旋矩形通道内的对流传热情况，发现小间距螺旋通道可以更好地降低壁面温度，同时加速效应被轻微地诱导。Li等［17⁃19］通过研究截断肋通道、双层通道和套管通道对超临界正癸烷强化传热性能，认为间距/高度比12.5～25 的肋片布局、相同流向双层通道、相同流向套管通道（内通道远离加热面）具有较强的换热能力。孙星等［20］研究了超临界正癸烷在螺旋管中的传热规律，发现螺旋管内侧温度降低，环向温度分布更均匀。黄世璋等［21］分析了超临界碳氢燃料在波纹管内的传热特性，表明波纹管内的对流换热系数可提升40%，温度和组分浓度径向分布更加均匀。另外，超临界碳氢燃料流动换热不稳定现象也备受关注，胡雪烈等［22］阐述了超临界碳氢燃料声学型、转捩型和物性型不稳定振荡类型以及触发机制。王彦红等［23⁃24］实验发现了竖直上升圆管内热声振荡现象，认为近壁流体密度和黏度的耦合作用是诱发主因，且热声振荡热通量随着质量流量和进口温度的提高而增加。严俊杰等［25］在竖直圆管内发现了两种不同的实验振荡现象（转捩型：阈值为Re=5 000；物性型：周期为8～15 s）。Sun 等［26］基于大涡模拟结果认为在浮升力影响下超临界正癸烷流动换热可分为3 个阶段。Sun 等［27］采用大涡模拟发现了超临界正癸烷振荡现象并科学地解释了发生机制。

上述超临界碳氢燃料对流传热研究，主要基于稳态工况或者长耗时下非稳态工况的稳定状态，且瞬态工况多为实验研究，然而鲜有报道针对初始瞬态工况下的碳氢燃料对流传热特性研究。Pizza⁃relli［28］认为超临界流体传热恶化及强化机理依旧不清晰。为此，本文采用大涡模拟（Large⁃eddy simulation，LES）方法，数值探究再生冷却通道内超临界正癸烷非裂解工况下流动传热初期的振荡现象，旨在进一步阐明超临界碳氢燃料的流动传热规律及物理机制，为空天飞行器再生冷却通道的可靠设计提供理论支撑，同时为其他超临界流体的流动传热研究提供有益借鉴。

1 物理模型的建立

超燃冲压发动机燃烧室主动再生冷却系统中，超临界碳氢燃料在燃烧室壁面内的矩形通道中吸收热量。选取截面尺寸为1.8 mm×1.8 mm、壁厚为0.6 mm 的矩形通道作为本研究的物理模型，如图1 所示。模型分为3 部分，150 mm（水力直径的83 倍）上游段、500 mm（水力直径的278 倍）测试段（即加热段）和150 mm（水力直径的83 倍）下游段，其中上游段和下游段可保证流动充分发展和抑制回流效应。流体竖直向上流动（重力加速度方向与其相反）。1.5 MW/m2的热流施加在单一壁面上，其余壁面设为绝热条件。入口质量流量为1.5 g/s，入口温度为473 K。出口设为压力出口，其值为3.0 MPa。流体域和固体域的交界面设为无滑移壁面边界。

图1 计算模型与边界条件Fig.1 Computational model and boundary conditions

2 数值方法

2.1 控制方程

超临界正癸烷在竖直矩形通道内的流动传热规律由质量守恒方程、动量守恒方程和能量守恒方程控制。大涡模拟数值计算方法本质是直接求解大尺度涡，而采用模型近似求解小尺度涡，其控制方程形式如下，具体符号表示参阅文献［26，29］。

2.2 物性参数

超临界正癸烷的物性参数（密度、比热、导热系数和动力粘度）从美国国家标准与技术协会（Na⁃tioanl institute of standards and technology，NIST）数据库REFPROP 中获取。具体地［30］，采用MAT⁃LAB 调用REFPROP 9.0 数据库来获取50 组温度⁃热物性参数值的数据点（压力变化范围很小，故忽略压力对热物性参数的影响），借助Fluent 软件中分段线性插值方法供用户自定义流体热物性，利用Journal 文件导入Fluent 软件，实现50 组热物性参数的数据点自动输入。固体域为不锈钢，其密度和比热分别为7 930 kg/m3和500 J/（kg·K），导热系数在12.1～28.5 W/（m·K）范围内变动（随着温度升高而变大）。

2.3 求解方法

图2 为流体域和固体域结构化网格局部示意图，设置方法详见文献［31］。为实现高精度计算需求，设定近壁区第一层网格高度为0.01 mm，量纲为-值y+＜1，流向网格间距Δz+= 50～100，展向网格间距Δx+= 10～20，近壁区网格增长率为1.05，全域网格总数为8.2×106。为捕捉边界层内瞬态流动信息，选取适应壁面的局部涡流黏度模型（Wall⁃adapting local eddy⁃viscosity，WALE）模型求解控制方程中亚格子粘性项。速度⁃压力耦合求解采用压力的隐式算子分裂法（Pressure implicit with splitting of operator，PISO）算法处理，时间项采用二阶隐式差分格式离散，对流项和扩散项采用二阶差分格式离散，湍流脉动采用涡方法处理。根据克朗条件（Courant⁃Friedrich⁃Le vy，CFL）计算时间步长［32］，其公式为

图2 截面网格及局部放大图Fig.2 Mesh of a cross-section and local magnification

式中：us为速度尺度，可视为入口流速，ls为网格单元尺度，最终确定时间步长为1×10-4s。设定数值模拟时长为1.5 s，内循环迭代步数为20，共计算30万步。

2.4 数值验证

现有实验结果多为稳态数据，需计算LES 稳态结果并进行数值验证。为节省计算资源，采用雷诺平均纳维⁃斯托克斯方程（Reynolds average navier⁃stokes simulation，RANS）收敛结果作为LES 初始场数据。利用文献［7］中的几何模型和实验数据验证LES 计算模拟精度。几何模型为2.05 mm×2.05 mm 水平矩形通道，壁厚0.95 mm，上游段100 mm，测试段150 mm，下游段25 mm。边界条件为qm= 162 kg/（m2·s），Tin= 620 K，pin= 3.0 MPa，qw= 103 kW/m2。选定矩形通道上壁面温度、下壁面温度和侧壁面温度为对比参数，计算结果与实验数据的对比结果如图3 所示。可见，数值计算的下壁面温度、侧壁面温度与实验数据吻合较好；上壁面温度略有增加，预测精度较低是由于该区域发生传热恶化现象的缘故［33⁃34］。总体而言，结果表明LES 数值方法可靠，可用于超临界正癸烷非常规流动传热特性分析。

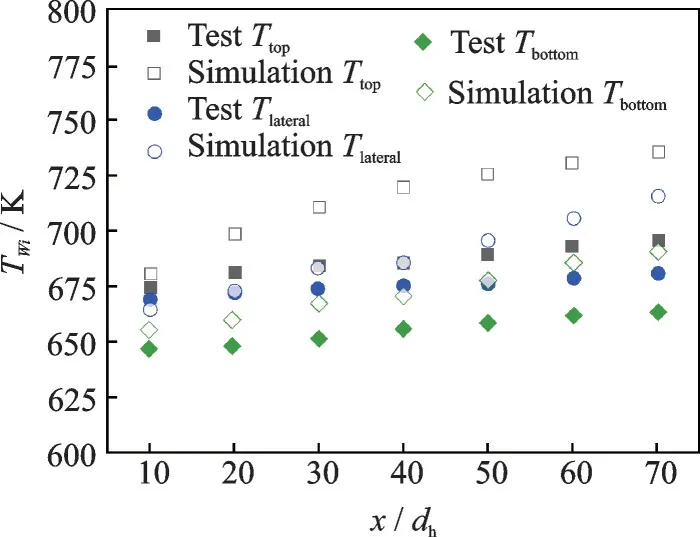
图3 大涡模拟数值结果和实验数据对比分析Fig.3 Comparative analysis between the LES results and experimental data

3 结果与分析

3.1 温度和速度分布特征

将测试段出口中心位置（［1.5，1.5，650］）作为监测点，其温度和速度随时间的变化规律如图4所示。在数值计算时长1.5 s 内温度和速度变化较大，但仍未达到稳定状态，证实超临界正癸烷在流动传热初期存在波动。特别地，在时间段0.6～1.1 s 内，温度陡增至峰值，随后下降至低谷，相应地，速度在相同时刻也存在波动。温度和速度之间不存在必然联系，即：0～0.6 s 流体温度保持不变，速度却先升高后降低；0.6～1.0 s 温度升高，1.0～1.1 s 温度降低，而0.6～0.7 s 速度降低，0.7～0.9 s速度升高，0.9～1.0 s 速度降低，1.0～1.1 s 速度升高；1.1～1.5 s 温度几乎恒定，速度降低。原因在于：（1）本研究工况速度波动性较大，类似于湍流流动的发展段；（2）靠近加热面的流体温度高，黏性系数降低，剪切应力减小，中心区域流体速度增大；（3）浮升力驱动二次流掺混上下壁面区域流体，进一步影响截面速度分布。

图4 给出0.1 s 间隔下温度和速度的波动轨迹，无法完全反映出真实变化情况。图5 给出了10-4s 间隔下1.4～1.5 s 内下游段出口截面平均速度分布，下游段出口截面平均速度产生的波动幅度与文献［23］中质量流量振荡相一致，出现近似三角函数式波动规律，如果与系统振动频率相近，形成共振效应会造成再生冷却通道破裂失效［22，35］。

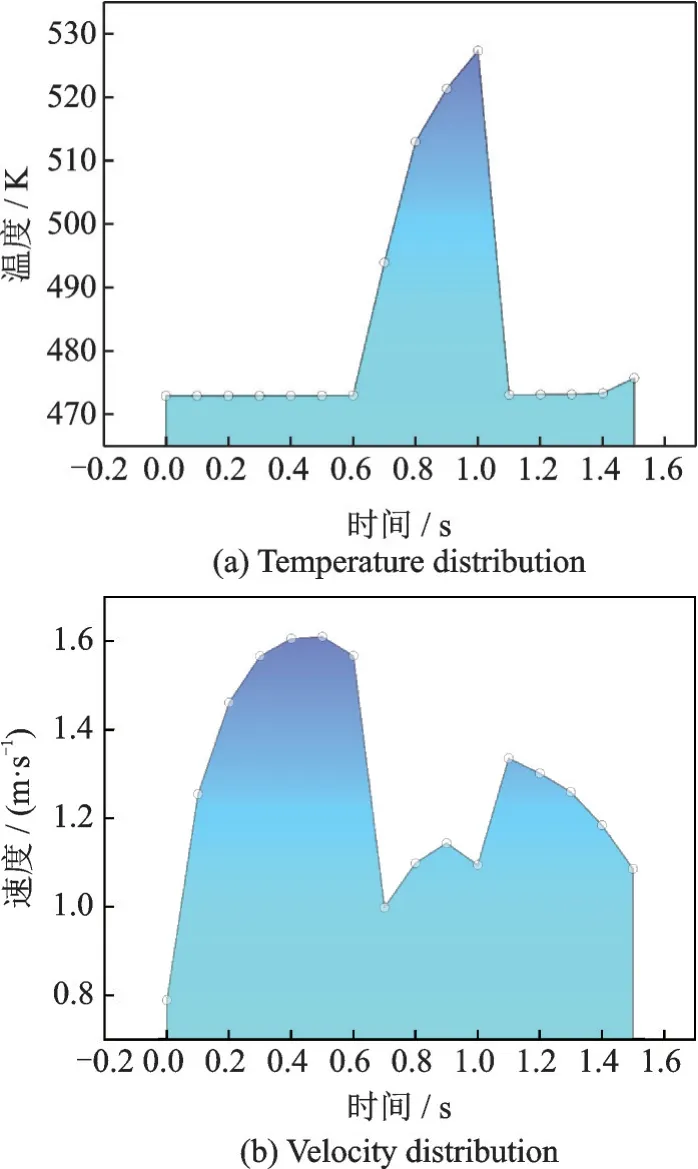
图4 点（1.5，1.5，650）处温度和速度随时间变化曲线Fig.4 Distributions of temperature and velocity along the time at point(1.5, 1.5, 650)

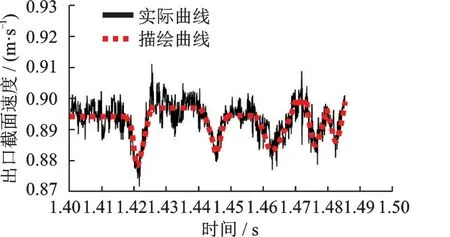
图5 时间段1.4～1.5 s 内下游段出口截面平均速度分布Fig.5 Average velocity distribution of the outlet section of the downstream section in the period of 1.4～1.5 s

图6 给出时间点0.5、1.0 和1.5 s 时线（［1.5，2.4，150］～［1.5，2.4，650］）与线（［1.5，0.6，150］～［1.5，0.6，650］）上的沿程壁面温度分布情况。线（［1.5，0.6，150］～［1.5，0.6，650］）上的壁面温度明显高于线（［1.5，2.4，150］～［1.5，2.4，650］上的温度，原因在于前者更加靠近加热壁面，热量无法有效传输。不同时刻两沿程壁面温度分布特征一致，随时间推移沿程壁面温度逐渐升高。0.5 s时壁面温度均匀分布，分别位于486 K 和670 K 左右；1.0 s 时沿程150～500 mm 范围内壁面温度分别位于545 K 和790 K 左右，1.5 s 时该沿程范围内壁面温度分别位于630 K 和880 K 左右；沿程500～650 mm 范围内温度均略有降低。相较于亚临界条件下的壁面温度分布规律，超临界态时后半程壁面出现温度下降趋势，说明此区域已出现传热强化现象。

图6 时间点0.5、1.0、1.5 s 壁面沿程温度分布Fig.6 Wall temperature distribution along the flow direc⁃tion at the time of 0.5, 1.0, 1.5 s

图7 给出时间点0.5、1.0 和1.5 s 时流体域中心线（［1.5，1.5，150］～［1.5，1.5，650］）上显著不同的温度和速度分布。0.5 s 时流体沿程温度保持不变，速度单调递增。1.0 s 时沿程150～620 mm 内温度保持不变，而后迅速上升再降低；速度保持轻微变化，而后迅速下降再产生波动。1.5 s 时温度在沿程150～610 mm 段保持不变，而后迅速增大再略微减小，速度沿程呈现降低趋势，在400～650 m段出现小范围波动。图4 中监测点［1.5，1.5，650］在t= 0.6 s 后温度才发生变化，表明t= 0.5 s 时热量还未传递到中心区域，沿程壁面温度保持不变。对于t= 1.0 s 和t= 1.5 s，中心区域温度发生变化，位置相较于t= 0.5 s 发生前移，分别位于z=620 mm 和z= 610 mm 处，表明热量持续地向中心区域传输。本研究侧重于瞬态初始工况，流动尚处于湍流发展阶段，呈现速度随机变化特征。总体上，温度和速度振荡区域出现在矩形通道后半程，表明主动再生冷却通道后半程较易发生非常规流动传热现象，原因在于通道后半程靠近壁面区域的温度处于拟临界温度附近（超临界正癸烷：拟临界压力3 MPa，拟临界温度为648.2 K），超临界正癸烷的物性参数发生剧烈变化，吸热能力提升。

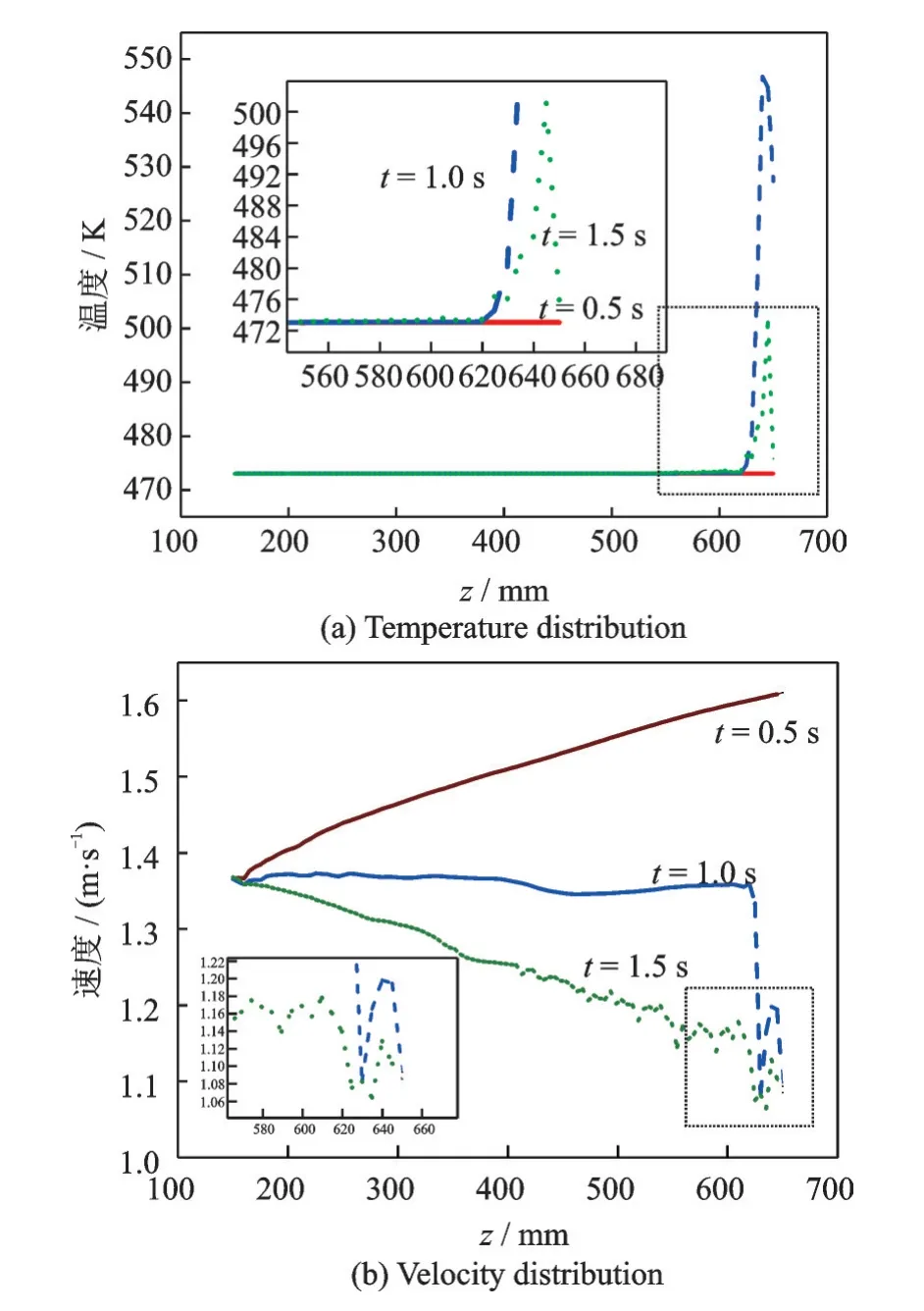
图7 时间点0.5，1.0，1.5 s 中心线（[1.5, 1.5, 150]～[1.5,1.5, 650]）沿程温度和速度分布Fig.7 Distributions of temperature and velocity along the centerline ([1.5, 1.5, 150]—[1.5, 1.5, 650]) at the time of 0.5, 1.0, 1.5 s

3.2 截面流线分布特征

为进一步探明沿程500～650 mm 处壁面温度明显变化（图6）的原因，图8 展示了z= 600 mm 截面处的流线及温度分布情况，其中流线用速度大小来表征。t= 0.5 s 时靠近加热面的流体温度增大，浮升力驱动流体从温度较高区域流向较低区域，远离加热面的位置，中心区域流体速度较大；t= 1.0 s时发现涡分布，原因在于靠近壁面的流体温度处于拟临界温度附近，物性参数剧烈变化，流体速度较大的区域开始下移，流向开始由远离加热面向靠近加热面转变，处于掺混状态；t= 1.5 s 时涡开始下移，低温流体开始冲击加热面，强化了传热效果。

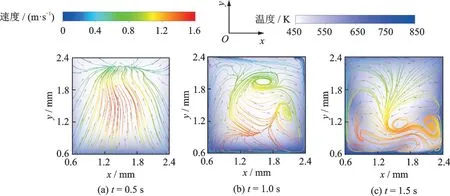
图8 不同时间点沿程截面z = 600 mm 处流线和温度分布Fig.8 Streamline with the magnitude of velocity and temperature distributions at the different cross-sections

3.3 涡的演化规律

为进一步揭示涡演化规律，图9 采用旋涡强度= 28 s-1来表征0.5、1.0、1.5 s 时涡核分布特征。t=0.5 s 时涡核主要集中在通道的中心且远离加热面位置，旋涡处温度较低，进口和出口处未观察到涡分布；t=1.0 s 时中心部位涡核消失，600～650 mm 段内出现大量涡核，500～600 mm 段内存在少许远离加热面涡核，相比于时刻0.5 s，温度有所增加；t=1.5 s 时涡核广泛分布，相较于t=0.5 s和t=1.0 s 时，涡核处于加热面附近，温度进一步升高。从t=0.5 s 到t=1.5 s 时，涡核实现由上壁面向下壁面的转移，增强加热壁面的传热效果，其原因在于靠近加热面的流体温度处于拟临界值附近，变物性流体紊乱程度加强。

3.4 动能分布特征

图10 给出了中心区域y‑z截面上的温度和动能分布。t=0.5 s 时靠近受热面的流体温度逐渐增大，动能呈现出中间大两端小的趋势。t=1.0 s 时由于固体域导热，远离受热面的流体温度逐渐增大，壁面处动量梯度被分为150～450 mm 段内小动量区域和450～600 mm 段内大动量区域，且出口处出现动量波动和温度波动现象。t=1.5 s 时加热面处流体温度接近拟临界温度，流体密度减小，动能和温度波动性较强。而未达到拟临界温度的区域，动能和温度未出现明显波动，说明流体物性的剧烈变化是诱导强波动的原因。图6 中波动引起壁面位置500～650 mm 处温度降低，振荡现象强化了流体与固体壁面之间的热传递。从图9 中可知振荡现象诱导大量旋涡，使热量传递得到有效保障。总之，振荡现象的存在有益于提升超临界正癸烷的对流传热性能。

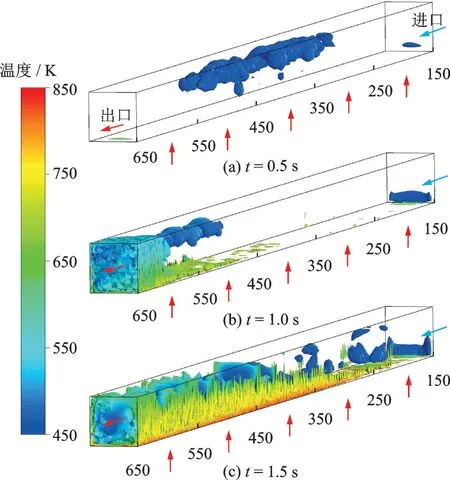
图9 不同时刻涡核分布Fig.9 Distribution of vortex core region at different time

图10 不同时刻截面y‑z 上的温度和动能分布（单位：mm）Fig.10 Distributions of temperature and kinetic energy of the y‑z cross-section at different time (unit:mm)

3.5 性能分析

为评估不同时刻超临界正癸烷在矩形冷却通道内的流动传热性能，本文采用平均努赛尔数和范宁阻力系数，计算公式为

式中：Nu为加热面平均努塞尔数，h为加热面平均传热系数，λave为基于进出口平均温度计算得到的导热系数，qw为加热面的热流密度，Tw_ave为加热面的平均温度，Tf_ave为进出口平均温度，Tin和Tout分别为进出口截面平均温度，f为范宁摩擦因数，Δp为通道压降，ρave为基于进出口平均温度计算得到的流体密度，uave为进出口平均速度，a，Lt分别为冷却通道的水力直径（即截面宽度）和测试段长度，uin，uout分别为进出口截面速度。

图11（a）给出了不同时刻努赛尔数分布，可以看到超临界正癸烷的平均换热能力随时间推移逐渐减小，0～0.5 s 时间内下降幅度较大，0.5～1.5 s时间内下降幅度较小。原因在于初始流体和加热壁面间大温差带走热量较多，后续两者之间小温差带走热量较少。图11（b）给出不同时刻范宁摩擦因数分布，亦出现如图5 所示的振荡现象，尽管两者之间时间间隔不同。作为描述流体所受阻力和推动力之间关系的范宁摩擦因数，它随时间呈现出三角函数式振荡，说明流体前进速度出现波动性，这直接导致流体动能出现振荡，进一步说明了超临界正癸烷出现振荡的原因在于摩擦因数的波动性。

图11 不同时刻平均努塞尔数和范宁摩擦因数分布Fig.11 Average Nusselt number and Fanning friction factor distributions at different time

4 结论

超燃冲压发动机燃烧室壁面的冷却依赖于主动再生冷却系统，超临界碳氢燃料于矩形通道内会发生不同于亚临界条件下的流动传热现象。由于缺乏流动传热初始瞬态实验数据，本文采用稳态工况下实验数据验证了长耗时稳定工况下的大涡模拟数据，进一步地，利用大涡模拟数值计算方法探究超临界正癸烷初始流动传热特性，并试图解释其发生原因。研究得到以下结论：

（1）超临界正癸烷流动传热初始速度和温度波动性较大，通过监测较小时间间隔的速度分布，发现振荡现象存在一定的频率和振幅。

（2）超临界正癸烷的总体换热能力随时间推移逐渐降低，矩形冷却通道500～650 mm 范围内的壁面温度有降低趋势，传热被强化，原因在于流体温度处于拟临界温度附近，物性发生剧烈变化，摩擦因数发生振荡性，流体动能也出现振荡现象，诱导产生涡使得远离加热面的冷流体开始冲击壁面，温度得以降低。

（3）应采用更小时间尺度的大涡模拟数值计算方法，探究超临界碳氢燃料非稳态流动传热过程，得到非稳态振荡频率和振幅及稳态涡型演化规律。