扩展卡尔曼滤波对时变参数追踪性能的影响研究

唐宏志，姜金辉

（南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016）

参数识别是动力学的第一类逆问题。参数识别问题按识别参数的种类可以分为模态参数识别与物理参数识别；而如果按识别参数的方法，可以分为时域法参数识别和频域法［1⁃2］参数识别。在时域内识别结构的物理参数，主要方法有扩展卡尔曼滤波（Extended Kalman filter，EKF）、H∞滤波［3］、蒙特卡洛滤波［4］和最小二乘估计（Least square esti⁃mate，LSE）［5⁃6］。EKF 是在经典卡尔曼滤波（Kal⁃man filter，KF）［7⁃8］的基础上改进得到的，文献［9⁃11］使用扩展卡尔曼滤波方法对多自由度线性结构的参数进行识别。文献［12⁃13］为了实现对结构时变参数的跟踪，采用自适应技术对EKF 方法进行了改进。文献［14⁃15］在载荷未知的情况下，将最小二乘法与EKF 方法结合，识别时变的结构参数，同时求出未知载荷。

这些文献都对扩展卡尔曼滤波方法进行了改进，但并没有提及滤波参数的设置对识别效果的影响，尤其是结构中参数会随时间变化的情况。事实上，随着算法的迭代计算，EKF 算法对测点响应的利用程度会越来越小，此时识别结果无法追踪到时变参数的变化情况。因此，必须选择恰当的滤波参数（模型噪声的协方差矩阵Q，测量噪声的协方差矩阵R）。本文首先介绍了一种结构参数识别方法，适用于外界载荷已知的情况，并试图通过仿真算例说明如何选择最优的滤波参数，来使得EKF算法对时变结构参数的跟踪性能达到最佳，即算法能快速、准确地识别出结构参数的变化情况。

1 结构参数识别方法

本文使用扩展卡尔曼滤波方法作为结构参数的识别方法。对于1 个n自由度的动力学系统，当结构中的未知参数，例如质量矩阵M，刚度矩阵K或阻尼矩阵C中的某些参数待确定时，参考卡尔曼滤波理论，将这些未知参数与状态向量x一起组成扩展状态向量z

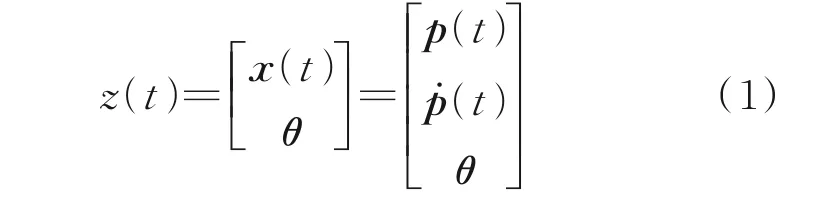
式中：θ为待确定的未知参数向量，长度设为m；x(t)表示状态向量，其长度为2n。令θ̇=0，此时，卡尔曼滤波理论中的状态更新方程可以重新写为

而测量更新方程的形式与观测量的类别有关，本文选择的测量类别是加速度信号。此时，测量更新方程可以写为

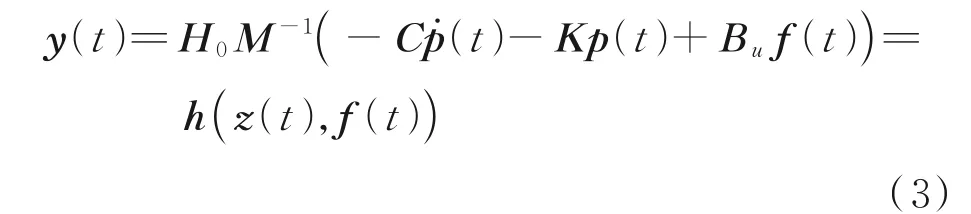
式中：M表示大小为n×n的质量矩阵；C表示大小为n×n的阻尼矩阵；K表示大小为的n×n的刚度矩阵；p̈(t)，ṗ(t)，p(t)分别代表结构的加速度向量，速度向量，以及位移向量，向量的长度为n；Bu代表激励的影响矩阵，与激励在结构上的作用位置有关，由0 和1 组成，它的矩阵大小为s×n；f(t)表示激励向量，长度为s；H0为由0 和1 组成的位置矩阵。由于质量矩阵M，刚度矩阵K或阻尼矩阵C包含了未知参数θ，这也就意味着关于扩展状态向量z(t)的状态更新方程fc(z(t)，f(t))是一个非线性方程，同样测量更新方程h(z(t)，f(t))也是一个非线性方程。

利用泰勒展开，将上述两个非线性方程（1，2）转化为多项式之和的形式，并略去高阶项，仅保留一阶多项式，由此可将非线性方程近似看成线性方程

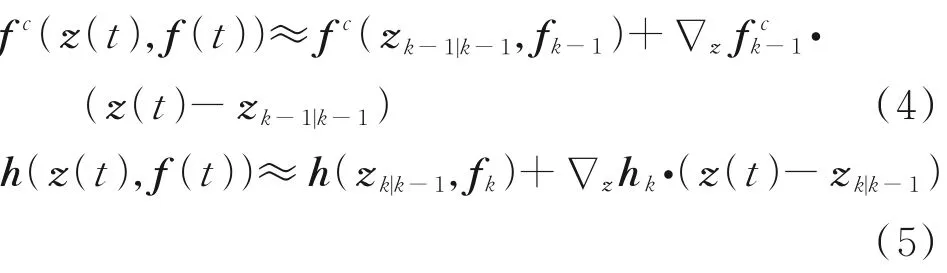
式中：zk-1|k-1为在tk-1时刻的扩展状态向量；zk|k-1为在tk时刻的扩展状态向量；∇z fc k-1为状态更新方程对扩展状态向量z(t)的一阶偏导；∇zhk为测量更新方程对扩展状态向量z(t)的一阶偏导，又称为雅各比矩阵。由泰勒展开定理可知，只要t时刻的扩展状态向量z(t)与zk-1|k-1，zk|k-1之间大小差距很小，式（4，5）就能近似成立。而要使z(t)与zk-1|k-1，zk|k-1的差距很小，只要时刻t与时刻tk-1，tk差距很小即可。

得到离散化的近似线性等式（4，5）后，与卡尔曼滤波理论的方法类似。首先是状态更新过程，其先验估计的均值和估计误差的方差可以写为

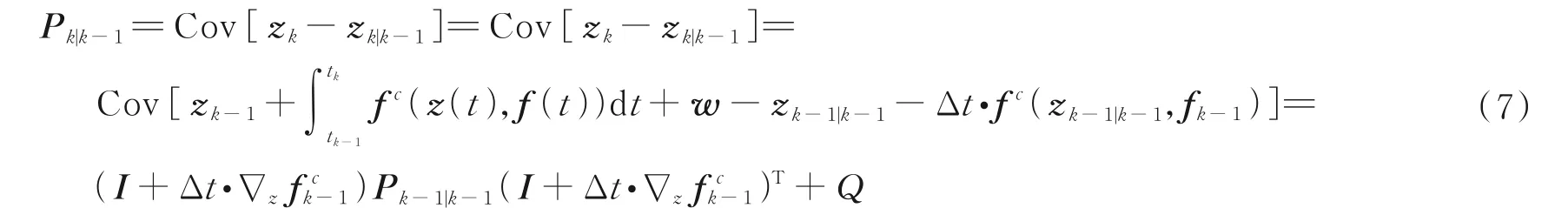
由式（7）可知，扩展状态向量中的参数θ在状态更新过程中并不会变化，仅凭该过程并不能实现时变参数的追踪。然后对于测量更新方程，后验估计的均值和估计误差的方差可以写为

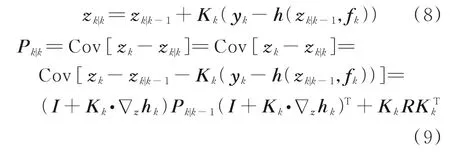
式中：Kk为卡尔曼滤波增益，它表示对测量响应的利用程度。通过方程（8，9）可以使得扩展状态向量zk|k中的参数θ发生变化。因此，可以认为扩展卡尔曼滤波算法是通过测量更新过程实现了对参数的追踪，只要加大对测量响应的利用程度，就能使zk|k较快地收敛到真实参数值。Kk其求法与卡尔曼理论中的相同，可以写为

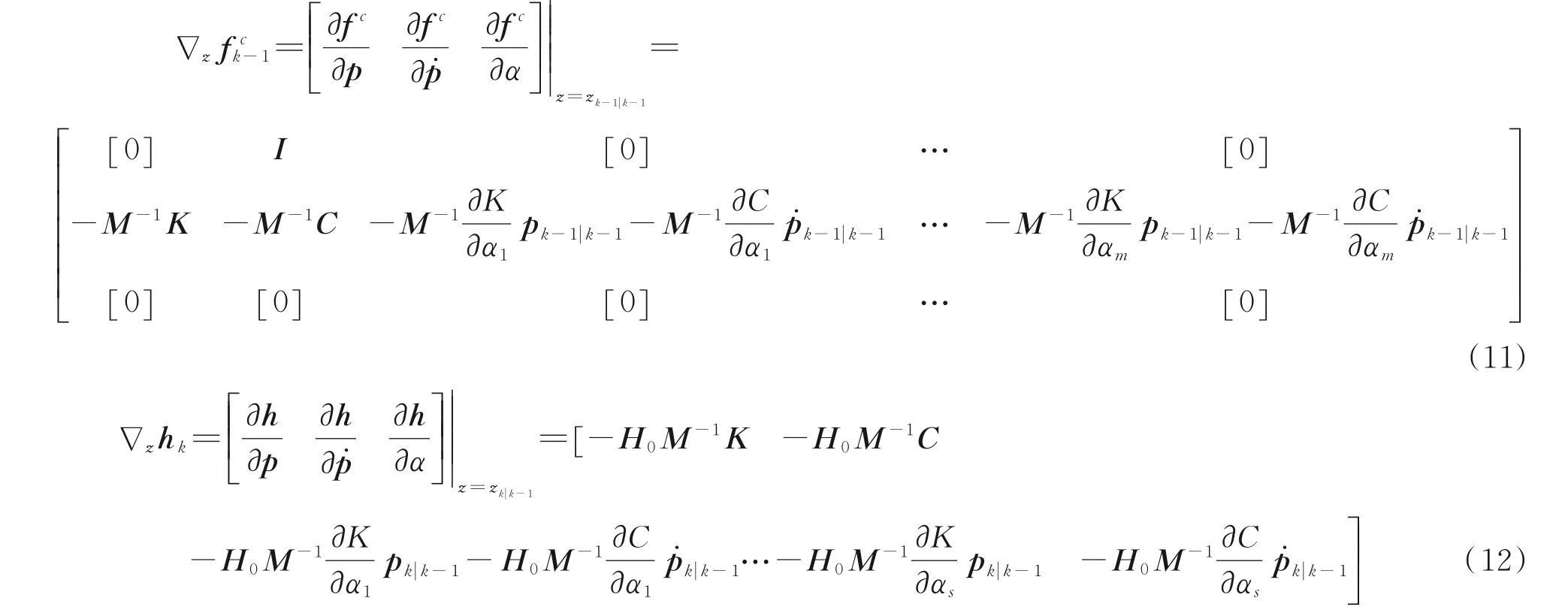
由此，可以得到扩展卡尔曼滤波算法的流程如表1 所示。

表1 扩展卡尔曼滤波法算法流程Table 1 Algorithm flow of extended Kalman filter

2 EKF 算法追踪结构时变参数的影响因素

在前文状态更新方程的推导中，假定未知参数θ不会随时间变化，即θ̇=0。这也就意味着仅凭状态更新方程，只能识别出时不变的参数，对时变参数或缓变参数是无法识别出来的。对于变化参数的追踪，是通过测量更新方程来实现的。卡尔曼滤波增益Kk表示了对测量更新方程的利用程度。若希望能实现对时变参数的追踪，则对测量更新方程的利用程度必须加大，总的宗旨是能尽量利用测量更新方程，即令Kk在迭代过程中仍保持较大值。

由卡尔曼滤波增益的计算公式可知，卡尔曼增益Kk由测量噪声方差R和Pk|k-1共同决定，初始时刻Kk偏大，对状态的估计主要依赖于测量更新方程。随着迭代过程的进行，测量对状态的修正作用不断减少，系统反而依赖于状态更新方程，此时Kk会逐渐变小。

为了使得滤波过程中，一直保持对测量更新方程的利用，需要选择合适的滤波参数。比如：模型噪声的协方差矩阵Q，对应状态向量部分的取值较小。对应参数部分的取值较大，这相当于告知滤波系统对结构未知参数的估计存在较大偏差，促使算法识别的结构参数会向真实值靠拢；测量噪声的协方差矩阵R的取值偏小，这相当于承认滤波系统所测量的响应具有很高的置信度，加大系统对测量更新方程的利用程度，从而加强算法对结构时变参数的追踪能力；然后是外界的测量噪声对参数识别效果的影响，算法能在响应存在噪声干扰的情况下识别出结构未知参数，这是通过调整测量噪声协方差矩阵R的方式来实现的；最后是观测点数的影响，选择悬臂梁作为仿真算例，由于悬臂梁既有转角自由度，又有竖向位移自由度，选择仅仅观测竖向位移自由度可以看出算法仍能较好地识别出结构参数变化的情况。

3 仿真算例

本文选择一个三自由度系统，如图1 所示，讨论模型噪声的协方差矩阵Q，测量噪声的协方差矩阵R的影响，与观测点数对算法跟踪参数性能的影响。

图1 三自由度系统Fig.1 A three degree of freedom system

在初始状态下，k1=k4= 200 N / m，k2=k3= 100 N / m；m1=m2=m3= 1 kg。并假设这个三自由度系统的阻尼是比例阻尼，且有C=αM+βK，α=0.05，β=0.02。在1.5 s 时该结构中的刚度k1从200 N / m 突然下降到150 N / m。假设激励作用的位置和形式已知，质量块m1受到激励f=sin(5π·t)+2·sin(2π·t)，由此可计算得到结构各自由度的响应。为了便于讨论，选取加速度响应作为测量向量，且不施加噪声到测量向量中去。使用本文提出的扩展卡尔曼滤波算法，此时激励已知（作用位置，幅值大小），而未知参数仅选择k1，则扩展状态向量z=[p ṗk1]T是一个7×1列向量。

由于参数是未知的，所以初始参数的选择必然会有较大误差，而结构的初始位移和速度（即状态向量）却可以事先测得，所以可以设定成真实值。相应的初始估计误差协方差P0|0关于状态向量的部分可以设定为一个较小的值，初始估计误差协方差P0|0关于参数的部分必须设定为一个较大的值。令初始扩展状态向量z0，初始误差方差P0|0分别写为

3.1 模型噪声协方差矩阵Q 的影响

讨论模型噪声协方差矩阵Q的取值对时变参数识别的影响。Q为一个7 阶对角矩阵，前6 阶对应的是状态更新方程对结构的位移和速度所产生的误差，第7 阶代表的是状态更新方程对参数k1所产生的误差。两者是不一样的，因此必须分开讨论。令测量噪声的协方差矩阵R为对角元素为10-4的三阶对角矩阵。首先考虑模型噪声的协方差矩阵Q参数部分取值的影响，假定Q关于状态向量部分的取值为10-10，关于参数部分的取值为x，即

x分别取值为1，10-1，10-2，10-3时，讨论其参数部分的取值对参数识别效果的影响。同样，为了讨论状态向量部分取值的影响，令Q关于参数部分的取值为10-1，关于状态向量部分的取值为x。EKF 算法识别参数的效果如图2 所示。

从图2 可以看出，模型误差Q关于参数部分倾向于取一个偏大的值，模型误差Q关于状态向量的部分倾向于取一个偏小的值。它本质上是使Kk保持一个较大的值，算法对参数的追踪性能也就会比较好；但Kk过大，会使得识别参数出现较大的波动。在本算例中，状态向量部分取值10-10是合适的；参数部分取值10-1是合适的。这样的参数设置能很好地追踪到参数的变化情况，且参数识别图也不会有太大的波动。

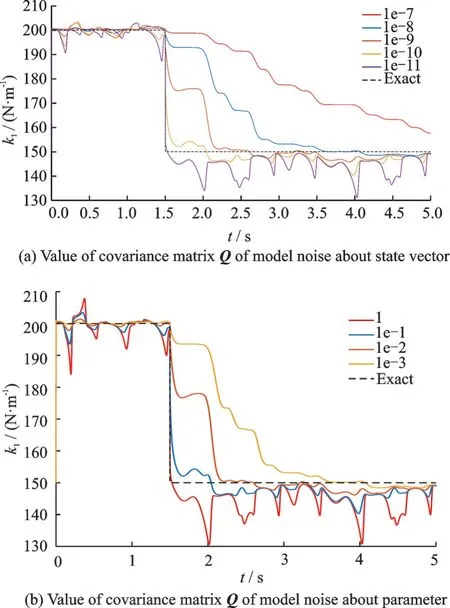
图2 模型噪声的协方差矩阵Q 对参数识别效果的影响Fig.2 Influence of covariance matrix Q of model noise on parameter identification effect

3.2 测量噪声协方差矩阵R 的影响

对于测量噪声的协方差矩阵R，其最优取值与测量向量中的噪声有关。现讨论对参数识别效果的影响。令模型噪声的协方差矩阵Q状态向量部分取值10-10，参数部分取值10-1。令测量噪声的协方差矩阵R为对角元素为x的三阶对角矩阵，当x取不同值时，参数的识别结果如图3 所示。

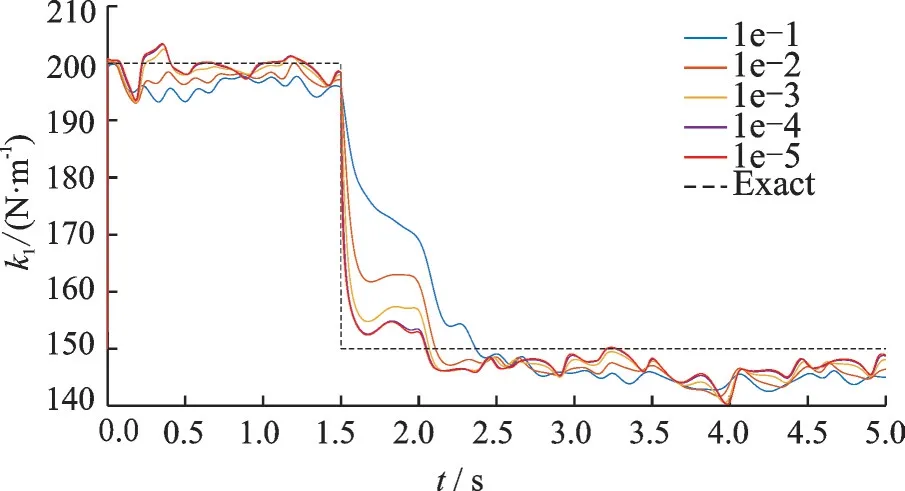
图3 测量噪声的协方差矩阵R 对参数识别效果的影响Fig.3 Influence of covariance matrix R of measurement noise on parameter identification effect

测量噪声协方差矩阵R取一个较小值时，此时卡尔曼滤波增益保持一个较大的值，算法的追踪参数性能较好。但值得注意的是，R的取值不能太小，它需要与观测向量中的噪声相适应，如果选择过小的值，导致这些估计的误差超过了实际误差，识别的参数必然不会与实际情况相同，严重时会发生发散。因此，需要为测量噪声协方差矩阵R取一个合适的值，确保算法能较快地识别出结构参数值，识别结果不会发散。

3.3 噪声影响

当响应中存在噪声干扰时，本文提出的算法仍能正确识别出参数变化情况。在此分别讨论测量响应中不含噪声与含有5%噪声的情况。令模型噪声的协方差矩阵Q状态向量部分取值10-10，参数部分取值10-1。由前文分析可知，测量噪声的协方差矩阵R的最优取值与噪声水平的大小有关。对于响应中不含噪声时，设定测量噪声的协方差矩阵R是对角元素为10-4的三阶对角矩阵，可以看出参数识别效果很好；而对于响应含有5%噪声时，此时R的取值必须大于10-4，与观测噪声水平相适应。若选取R是对角元素为10-2或10-3的三阶对角矩阵，可以看出算法能较好地识别出参数变化情况。

由图4 可以看出，无论测量向量中是否包含噪声，算法实践对时变参数的追踪是通过调整测量噪声协方差矩阵R的方式来实现的。

图4 测量噪声对参数识别效果的影响Fig.4 Effect of measurement noise on parameter identification

3.4 观测点数影响

为说明观测点数的影响，取一个悬臂梁作为仿真对象，梁长度L=1 m，矩形横截面尺寸为宽b=0.1 m，高h=0.01 m，材料密度ρ= 2 770 kg/m3，弹性模量E=71e+9 Pa，设悬臂梁的阻尼特性为瑞利阻尼，且有α=1，β=8e-7。再由公式I=b·h3/12，A=b·h可以推得该悬臂梁的截面惯性矩I与面积A。该悬臂梁的示意如图5 所示。

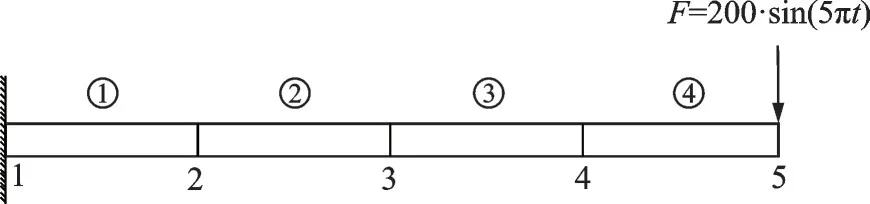
图5 悬臂梁结构Fig.5 Cantilever beam structure

由图5 可知，该悬臂梁被划分为4 个单元，它的总体刚度矩阵和总体质量矩阵是由各个单元的刚度矩阵Ki与单元质量矩阵Mi组合而成的。因此该悬臂梁既包括转角自由度，又包括竖向位移自由度，即4 个转角自由度和4 个竖向位移自由度。其中Ki，Mi可写为

为了便于讨论，把梁单元的刚度特性Ei Ii作为单元发生刚度变化的指标。假定梁单元①的刚度特性E1I1在第1.5～3.5 s 发生线性下降，下降至原来值的70%。其他单元的参数并不发生变化。在响应中添加1% 的白噪声，利用本文所提出的算法，把该悬臂梁前3 个单元的刚度特性作为未知参数向量，即扩展状态向量为z=[p，ṗ，E1I1，E2I2，E3I3]T，依次识别出各个刚度系数。

选择只观测第2，3，4，5 节点上的竖直加速度，不测量转角自由度，因此这也算是部分观测。设模型噪声的协方差矩阵G，以及测量噪声的协方差矩阵R分别为

观测全部测点与部分测点的区别仅需改变测量方程中的位置矩阵H0。若选择只记录结构的竖向加速度响应，因此可写为

同理可求出既观测转角自由度，又观测竖向自由度情况下的参数识别效果，由此可得参数识别结果如图6～8 所示。

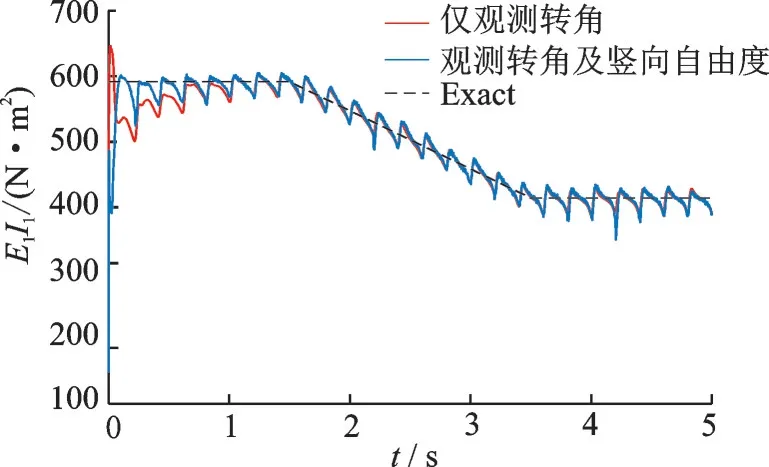
图6 刚度系数E1I1识别效果图Fig.6 Identification effect of stiffness coefficient E1I1

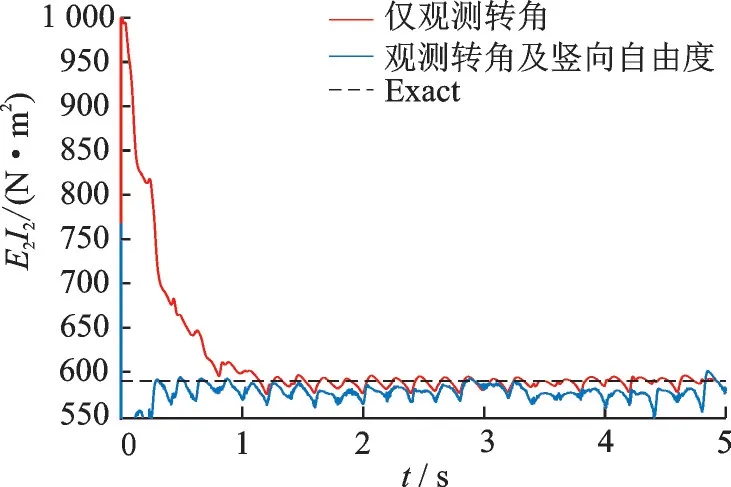
图7 刚度系数E2I2识别效果图Fig.7 Identification effect of stiffness coefficient E2I2

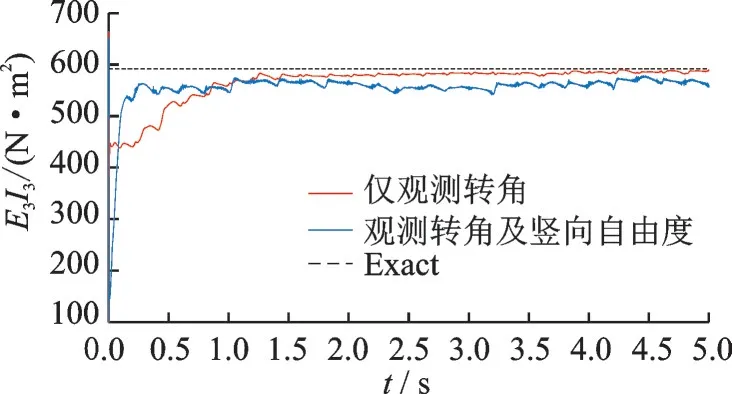
图8 刚度系数E3I3识别效果图Fig.8 Identification effect of stiffness coefficient E3I3

由图6～8 可以看出，在含有噪声的情况下，仅观测部分测点也能追踪到结构参数的变化情况，且效果比较好。这说明了扩展卡尔曼滤波算法能在测点部分观测的情况下识别参数变化。

4 结论

在载荷已知的情况下，扩展卡尔曼滤波算法对结构参数的识别主要是通过测量更新方程实现的，而卡尔曼滤波增益Kk表示了算法对测量更新方程的利用程度。为了实现算法对时变参数的追踪，本文提出了通过设置合适的滤波参数来保持较大的Kk。这其中包括：模型误差Q关于参数部分取较大值，模型误差Q关于状态向量的部分取较小的值。还讨论了测量噪声对参数识别效果的影响，测量噪声的协方差矩阵R必须与测量噪声相适应，并尽量选取一个较小值。仿真结果表明，这样的滤波参数设置使得EKF 算法在运行过程中能保持对测量更新方程的利用，从而能追踪到结构参数的变化情况，识别结构的时变参数。最后，通过悬臂梁仿真算例，证明了在部分测点观测的情况下，算法也能较好地识别出结构的参数变化情况，体现了EKF 算法的优越性。