基于改进A*算法的仓储环境AGV路径规划
牟德君,初鹏祥
(燕山大学 机械工程学院,秦皇岛 066004)
国外kiva 仓储AGV[1]在亚马逊大规模成功应用之后,国内近年也开始建造大型仓库,并在仓库中使用AGV 代替人工,实现“货到人”拣货方式[2]。
拣选任务完成分配后,需要进行AGV 的全局路径规划,常见全局路径规划方法有A* 算法[3]、蚁群算法[4]、RRT 算法[5]等,A* 算法具有简单,计算量小等优点,仓储环境中是横纵方向通道,不受A* 算法规划路径多转折,不够平滑的缺点影响,所以十分适用[6]。
目前大部分的仓储AGV 采取的路径规划方法仍是传统A* 算法或其他简单算法,而随着仓储行业的集群效应,仓库规模的扩大以及同时工作的AGV 数量的增多将会引起单个拣选任务执行时间长,从而导致仓货滞留[7],为了提高仓储环境的工作吞吐量,需要采用多个方面的改进来提高效率,而其中对路径规划算法的改进是很重要的。
针对A* 算法的改进方面多种多样,第1 类是改变评价函数:通过改变A* 算法评价函数的具体计算方法,减少寻路时间[8-9];改进评价函数的权重比例,以此减少生成路径的冗余点和拐点[10];在评价函数中加入新的系数,来考虑其他方面的影响[11]。第2 类是算法融合[12],文献[13]增加了一个预处理的过程,通过跳点搜索算法挑选出一批有代表性的跳点,改进算法通过连接跳点,可以实现较长距离的跳跃;文献[14]提出一种基于启发信息扩展节点的A*算法与混合蚁群算法相结合的路径规划方法,通过基于启发信息的节点扩展函数,解决A* 算法扩展节点时,会造成无用计算的问题。第3 类是对规划的方向进行改变[15],采取更多可选择角度来提高路径的平滑度,获得最优解。第4 类是对已规划路径进行处理,采用删除无用节点的方法[16]或是采用不同处理方式对路径进行优化使路径更平滑[17]。
本文中针对大规模仓储环境中面积大、AGV 数量众多而导致长时间等待甚至死锁的情况,以总工作时间最短为目标改进A* 算法,构建时间评价函数;引入转向代价,减少转向;引入拥堵代价,避免局部交通量大的路段发生拥堵甚至死锁情况;对评价函数进行自适应加权,使搜索前期可以快速收敛,后期避免陷入局部最优,最终提高AGV 拣货工作效率。
1 地图建模
本文基于栅格法建立了包含可移动式货架、拣选台、移动式物流机器人等硬件设备的智能仓库简化示意模型,如图1所示,仓库由4 行6 列的4×8货架组成,即图中黑色标识的栅格部分。在货架之间以及货架与拣货台之间的通道中同时穿梭着多个移动机器人,图中空白灰色栅格表示可移动通道,最左侧方块代表AGV 的充电处,也是起始位置,最右侧方块代表拣货台。

图1 仓库栅格地图Fig.1 Warehouse raster map
选择的货架布置格式是4×8 格式,内外双层,当机器人需要搬运内层的货架时,需要先将外层的货架搬开。选择这种布置方式的优势是可以节省大量的空间。而在搬运外层货架时会阻塞纵向通道,所以选择双排的纵向通道,在货架搬运过程中不会影响对向的机器人正常运动。通道是双向单行道,规定单向运行,运行方向和车道相同,采用单向道可以避免正面碰撞。
2 改进A*算法
在进行全局路径规划时采用A* 算法,为了实现总工作时间最短的目标,针对仓储环境对传统算法进行一些改进,采用曼哈顿距离计算路径距离。
2.1 采用时间代价
原算法采用距离代价来表示评价函数,不够直接,为了方便和其他代价相加时单位的统一,引入时间代价构建评价函数:
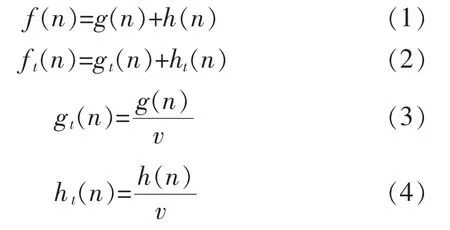
式(1)为A*算法的评价函数,v 为AGV 运行速度,在正常行驶时速度恒定;式(2)是构建的和时间代价相关的评价函数。
2.2 引入转向代价
在AGV 转向时需要经历一段减速—停车—加速的过程,引入转向代价,减少路径的转向能有效降低工作时间,节省能源消耗。

式中:α 为转向时间系数;T 为单次转向所需时间;ct为转向时间代价。
2.3 引入拥堵代价
在某一时间一片区域的小车达到一定数量后就会产生拥堵,当产生拥堵时,AGV 需要停车等待或者重新规划路径进行绕行,甚至产生死锁。引入拥堵代价改善拥堵情况:

式中:load(t)表示该时间段内所有未完成路径中该节点的出现次数;β 为将负载转换为负载代价的转换系数。
在交通管理方面常用来进行交通拥堵判断的拥堵判断参数有交通量、道路交通容量、交通流密度、空间占有率和车辆速度等[18]。其中交通量是在一段时间内经过某一截面车辆的数目。针对建立的仓储栅格地图,选择交通量作为判断参数,将交通量定义为在一段时间内经过某一可通行栅格AGV 的数目。如果1 个AGV 在1 个栅格上停留,则经过1 s则数目加1,统计出该栅格60 s 的load(t)。
根据测试效果将交通拥堵程度分为4 级,如表1所示,在load<10 时,说明该栅格畅通,不需要附加惩罚,此时负载转换系数β 设为0;在10≤load<15 时,该栅格轻度拥堵,此时在有其它道路具有相同的路径代价而拥挤程度更低的情况下,应选择其它的路径,负载转换系数β 设为0.1;在15≤load<20时,该栅格拥堵,此时应使AGV 尽量绕开该点,避免进一步的拥堵,负载转换系数β 设为0.3;在load≥20 时,该栅格严重拥堵,此时如果能找到其它路径就不要经过该栅格,负载转换系数β 设为10。

表1 拥堵程度分级Tab.1 Congestion classification
2.4 加权归一化
在搜索前期,希望能快速找到方向,让h(n)的权重系数占比增大。在路径接近目标时,为避免整个算法陷入局部最优,让g(n)的权重系数占比增大。对评价函数进行加权归一化处理。最终改进A*算法的评价函数为
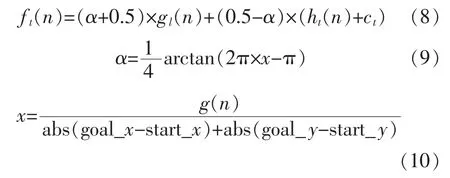
式(10)中:(start_x,start_y)为起点坐标;(goal_x,goal_y)为终点坐标。α 函数如图2所示,随着搜索路径g(n)增大,x 随之增大,α 也增大。

图2 权重函数Fig.2 Weighting function
3 仿真验证
采用Matlab2014b 进行仿真,验证各个部分改进的有效性和合理性。首先验证引入转向代价的效果,设定转向时间为1 s,转向时间系数设为1.5,为了明显验证算法改进的效果,构建30×30 的复杂栅格地图,模拟拥堵或存在其他AGV 工作时的复杂环境,在复杂地图中规划的路径如图3所示。
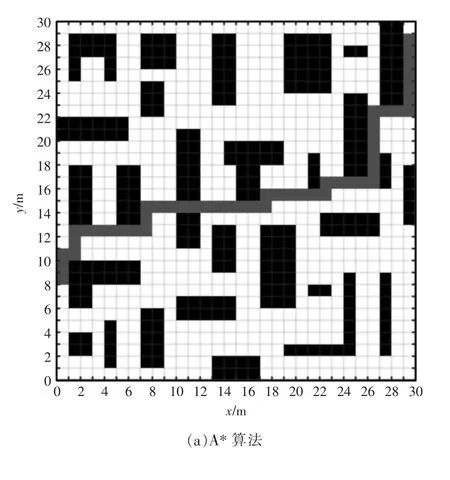

图3 复杂地图中的路径Fig.3 Paths in complex maps
由图3(a)可以看出传统A* 算法在寻找路径时共进行了12 次转向,由图3(b)可以看出改进的A*算法在寻找路径时共进行了6 次转向,在路径代价相同的情况下,转向的时间代价减少了一半。
为验证改进算法对不同拥堵的躲避情况,构建拥堵负载地图,如图4所示。记录每个栅格的load(t)。给图4中单独栅格处设为1 号栅格,添加load(t)为10,使该处栅格处于轻度拥堵情况。
图4(a)中为传统算法规划的路径,采用改进算法选择了另一条同路径消耗的路径,避开了负载更高的1 号栅格。


图4 导入负载地图后的路径Fig.4 Path after importing the load map
两个路段都处于相同拥堵程度时的路径如图5所示,在图5中对两个最短路径的一部分路段赋予相同的负载,比较在不同拥堵情况下规划的路径情况。
设图5(a)中两个单独栅格为负载栅格,都添加负载load(t)为20,使栅格处于重度拥堵情况,采用改进算法规划的路径选择了绕远路径而避开拥堵区域;在图5(b)中两负载栅格都添加负载load(t)为15,使该处两栅格处于相同拥堵情况,采用改进算法规划的路径和传统算法相同,不会导致路径非最优。


图5 两个路段都处于相同拥堵程度时的路径Fig.5 Path when both sections are at same level of congestion
对比算法改进前后规划相同路径所需要的时间,共选择8 组路径,起点和目标点用该栅格点编号表示,验证系数加权归一的效果如表2所示。
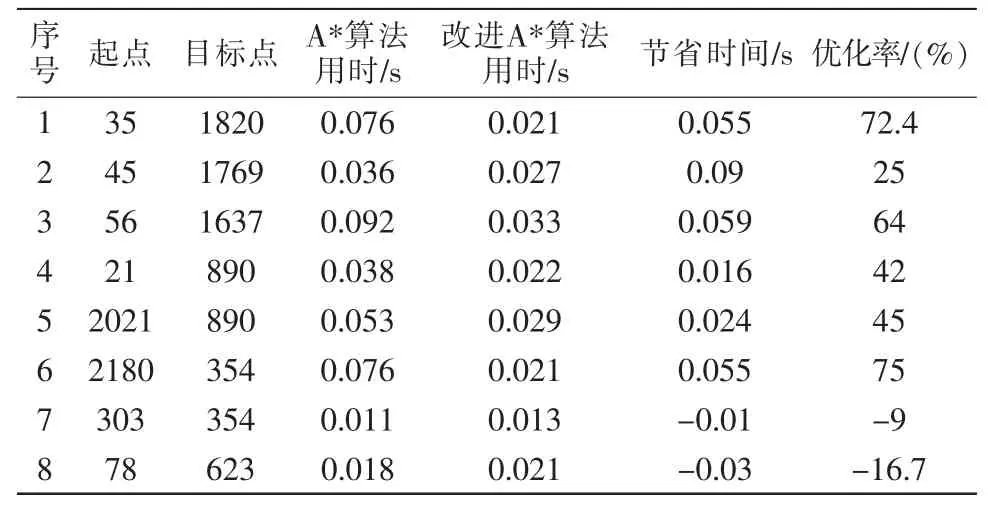
表2 A*算法和改进A*算法路径规划用时Tab.2 A* algorithm and improved A* algorithm path planning time
由表2可以得出,在路径较长时,改进算法规划时间要短于传统算法,由于规划用时较长,改进算法节省的时间也很多,在路径较短时,改进算法规划时间略长于传统算法,但差距不大。因为仓储环境很大,拣货任务中也需要规划从货架到拣选站台的往返长距离路径,所以改进后算法更适用于建立的环境模型。
4 结语
针对仓储环境中的多AGV 进行路径规划,对传统的A* 算法进行改进,首先为了满足总体的工作时间最短的目标以及同其他的引入代价具有相同的单位,采用时间代价代替路径距离代价构建目标函数;为了减少路径的转向,引入转向代价,减少路径代价相同时转向消耗;其次考虑局部地区交通网拥堵带来的长时间等待以及死锁情况,引入拥堵代价,选择其他路径躲避拥堵路段;最后引入加权系数,加快前期搜索速度,而在搜索后期减慢搜索速度,避免局部最优。

