具有梯度源和非局部源的反应扩散方程解的爆破时刻下界*
沈旭辉
(山西财经大学 应用数学学院,太原 030006)
引 言
在过去的几十年中,由于在物理学、化学、生物学以及其他应用学科中的广泛应用,反应扩散方程解的爆破现象成为研究的热点.许多学者研究了解的整体存在、有限时刻爆破及解的定性分析等并取得了一系列有意义的成果(参见文献[1-4]).众所周知,当方程的解在有限时刻发生爆破时,对于爆破时刻的估计具有很大的实际意义.关于爆破时刻的上界已有大量的研究,特别是在文献[5]中,作者概括性地给出了几种寻找爆破时刻上界的方法.然而在实际问题中,仅知道爆破时刻的上界是不够的;从安全地控制实际生产的角度来说,爆破时刻的下界可以给出安全的控制时间,因此研究爆破时刻的下界更加有意义但也更加困难.Payne 等在文献[6]中首次给出解的爆破时刻的下界.此后,学者们研究解的爆破时刻的下界并取得了丰富的成果[7-12].据笔者所知,目前许多研究解的爆破时刻下界的工作集中在Ω ⊂R3上 .关于在Ω ⊂Rn(n≥2)上,解的爆破时刻下界的研究不多,而对于具有梯度源及非局部源的反应扩散方程的爆破时刻下界的研究则更少.本文研究了下列具有梯度源和非局部源的反应扩散方程解的爆破现象:
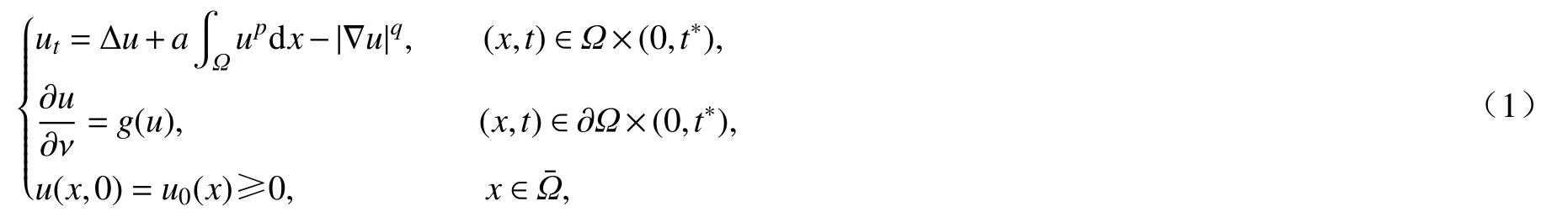
其中Ω为 Rn(n≥2)上 带有光滑边界的有界凸区域,为Ω的闭包,t∗为 可能发生的爆破时刻.令 R+=(0,∞),假设a为正常数,g(u)∈C1()为 非负函数,u0∈C1()为初始值且满足相容性条件.
对于已有的诸多研究,我们主要关注文献[13-14]中的工作.Song 在文献[13]中研究了下列问题解的爆破现象:
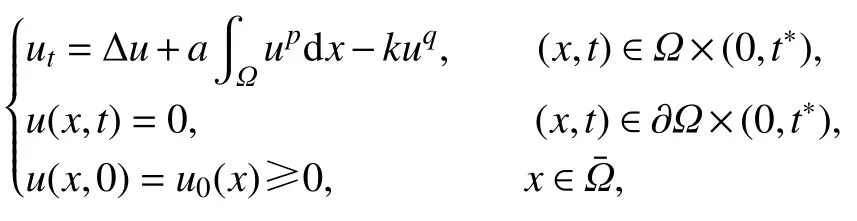
其中 Ω ⊂R3为带有光滑边界的有界凸区域.通过使用Sobolev 不等式和微分不等式技术,其给出了爆破现象发生时解的爆破时刻的下界.Marras、Vernier Piro 等在文献[14]中讨论了下列问题解的爆破现象:
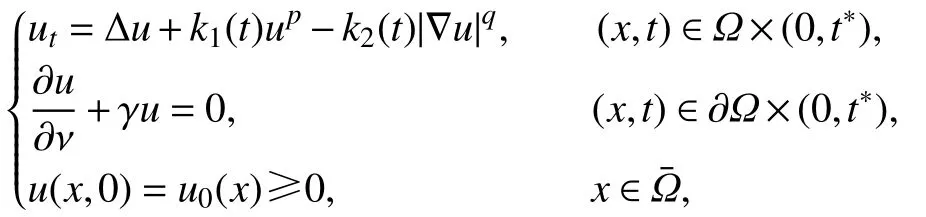
其中区域Ω ⊂Rn(n≥2)为有界光滑凸区域.当Ω ⊂R3时,作者在合适的假定之下给出解的爆破时刻的下界估计.
受上述文献工作的启发,我们研究了问题(1)解的爆破现象.首先,问题(1)的研究具有重要的理论背景和实际意义,它不仅可以描述一些热力学问题,而且可以用来解释一些生活在特定区域内生物种群密度(如细胞、细菌等)的演化问题.对于一个种群而言,物种的密度受种群中个体生长因素的影响,其中个体自身的生长不仅受其自身周边物种的影响,而且还受到与整个区域内其他物种之间的竞争关系的影响.因此,建立非局部源则更加符合实际.其次,对种群密度而言,个体的意外死亡因素也是不可忽视的,从而可以借助梯度源− |∇u|q来描述物种的意外死亡.有关具有梯度源和非局部源的反应扩散方程读者还可以参考文献[15-17].再者,据笔者所知,目前还没有文献针对问题(1)的爆破时刻下界进行估计.因此在本文中,我们将考虑具有梯度源和非局部源的反应扩散问题,通过构造合适的辅助函数,利用微分不等式技术和Sobolev 不等式,分别给出当爆破现象出现时,在Ω ⊂Rn(n≥3)和 Ω ⊂R2上解的爆破时刻下界.
本文的结构安排如下:在第1 节中,当 Ω ⊂Rn(n≥3)时,我们给出解的爆破时刻下界;在第2 节中,当Ω ⊂R2时,我们导出解的爆破时刻下界;在第3 节中,我们给出具体的实例应用来解释文中取得的抽象结果;第4 节对全文进行了总结.
1 在Ω ⊂Rn(n≥3)上解的爆破时刻下界
在本节中,我们给出有界凸区域Ω ⊂Rn(n≥3)上问题解的爆破时刻下界.为此我们假设

其中b为正常数.此外,还假设常数p>1,q>2且满足

定义下列辅助函数:
其中

此外,我们还将使用下列Sobolev 不等式(参见文献[18]):
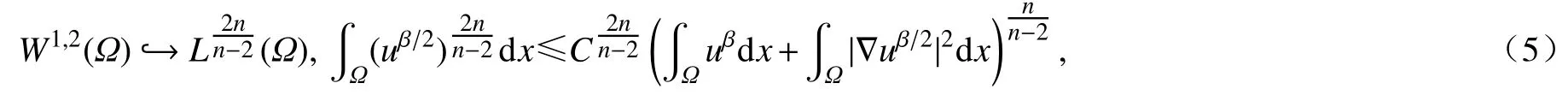
这里C=C(n,Ω)为依赖于空间维数n和区域Ω的常数.下面给出本节的主要结论.
定理1设u是问题(1)的一个非负经典解,假设条件(2)~ (4)成立.如果方程的解u在有限时刻爆破,则有爆破时刻的下界为
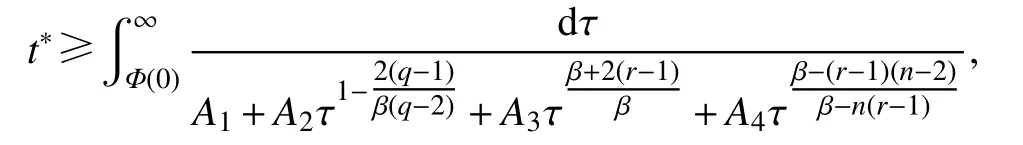
其中
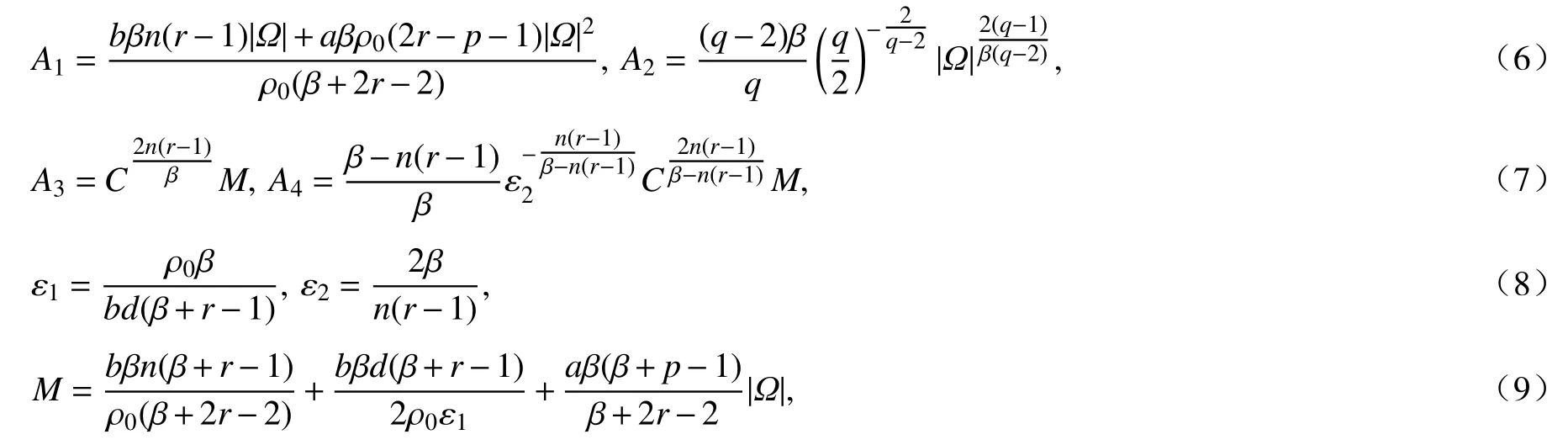
且ρ0=min∂Ω(x·ν),d=maxΩ¯|x|.
证明使用条件(2)、(4)及散度定理,我们有
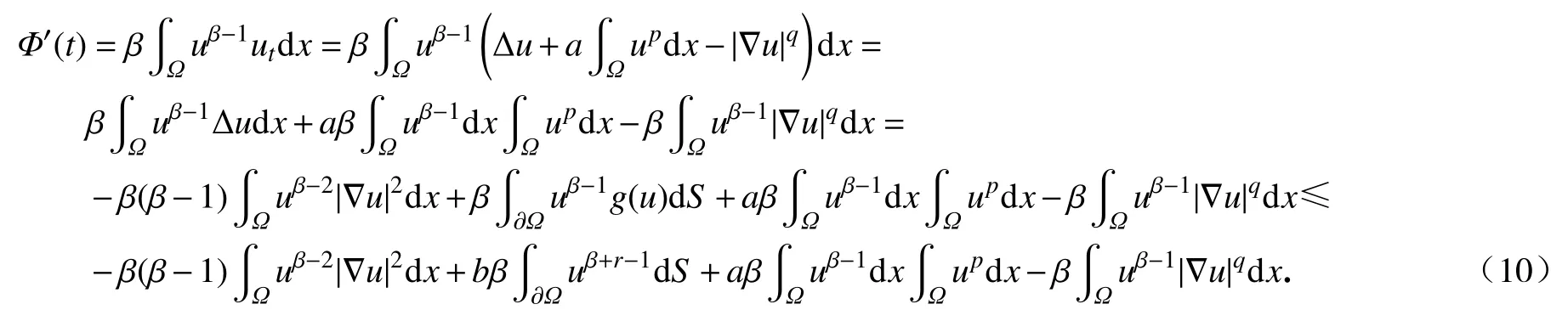
运用Hölder 不等式推出
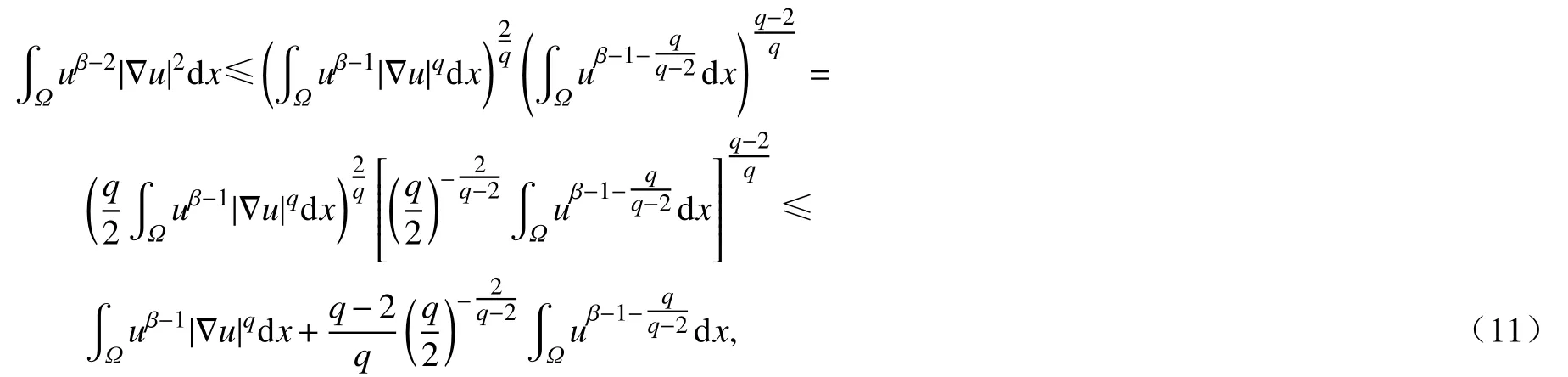
等价于
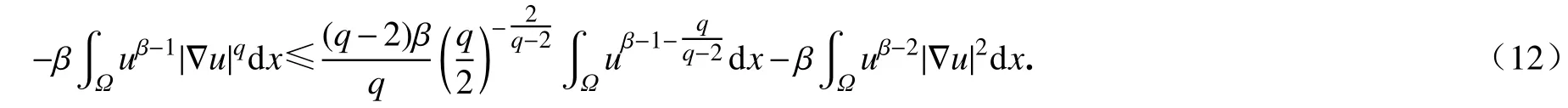
将式(12)代入式(10)中可得
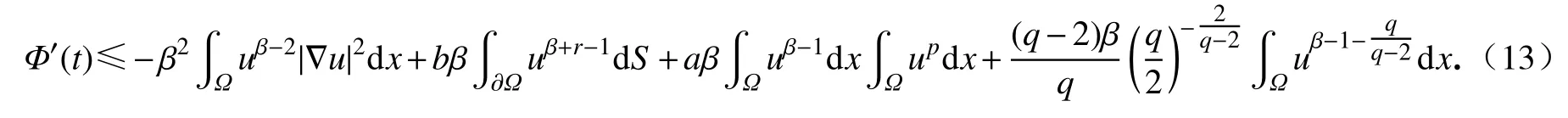
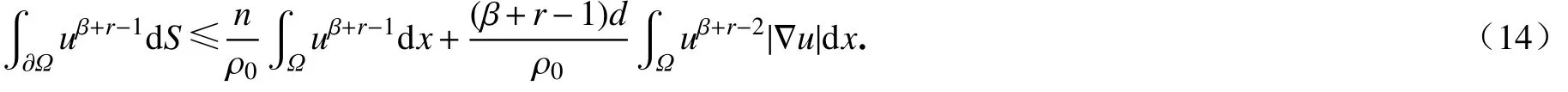
利用Hölder 不等式和Young 不等式,有
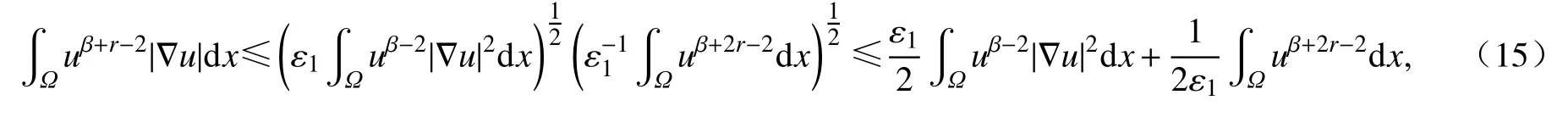
其中 ε1在式(8)中给出.将式(14)、(15)代入式(13)得
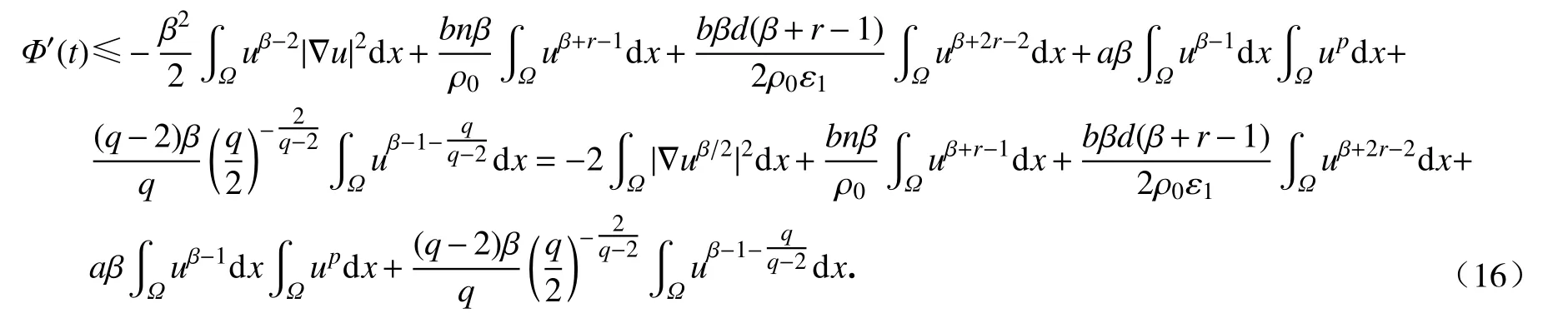
使用条件(3)、(4), Hölder 不等式及Young 不等式,我们有

联合式(16)~ (19),得到
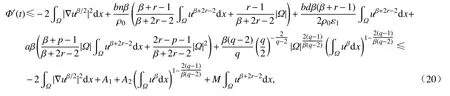
其中A1,A2在式(6)中给出,M在式(9)中给出.
接下来,我们估计式(20)中的第四项.使用Sobolev 不等式以及Hölder 不等式得到
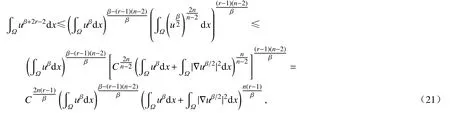

我们有
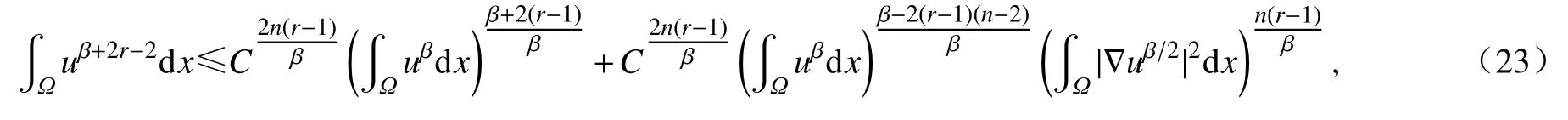
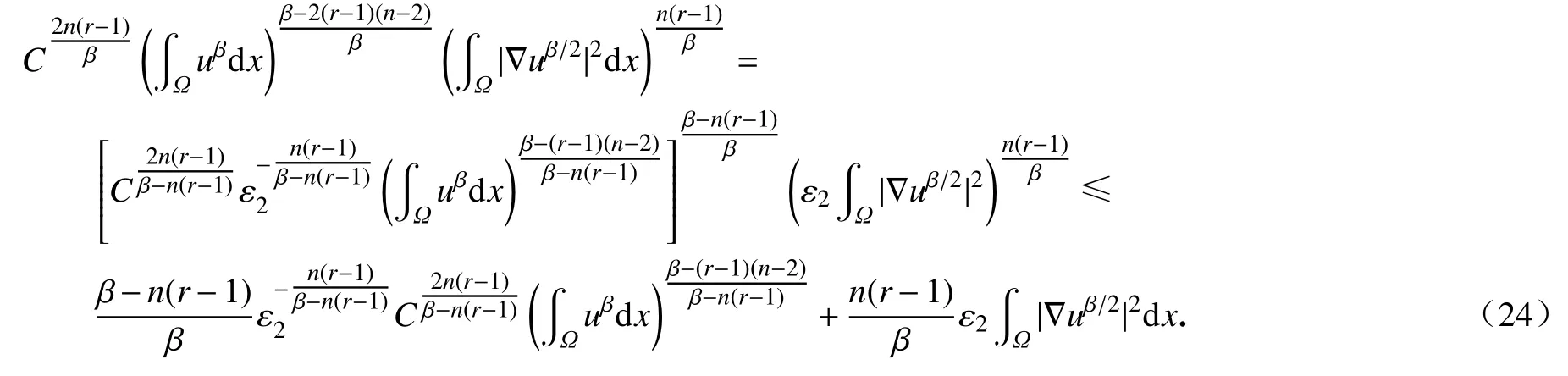
将式(23)、(24)代入式(21)可得
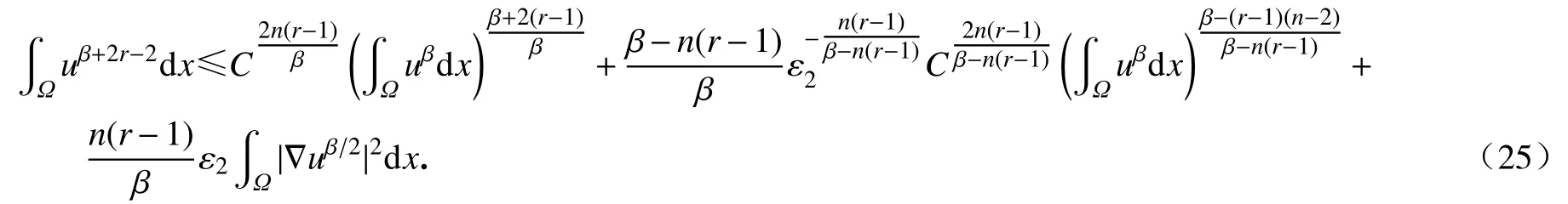
联合式(20)及式(25)推导出
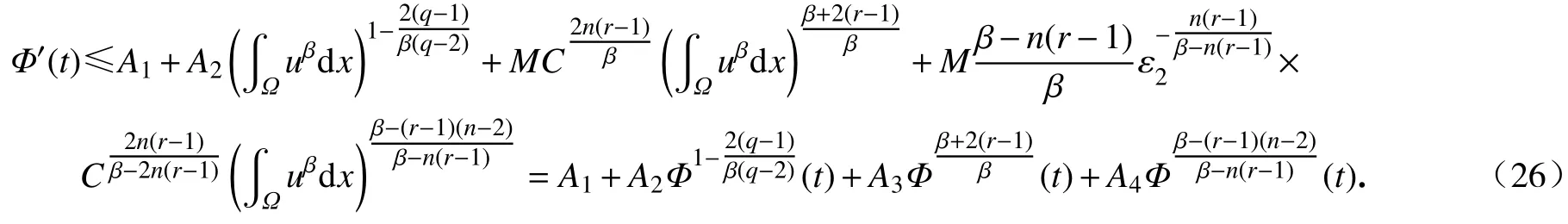
对式(26)两边从0 到t积分,得
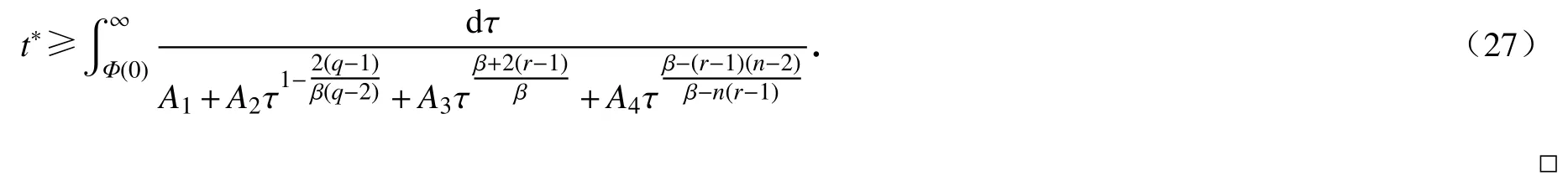
2 在Ω ⊂R2上解的爆破时刻下界
本节中,我们在Ω ⊂R2上给出解的爆破时刻下界.这里仍然假设条件(2)、(3)成立.定义下列辅助函数:
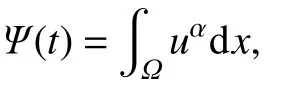
且

当n=2时,由于式(5)中的嵌入定理不再成立,因此我们使用下列嵌入定理:
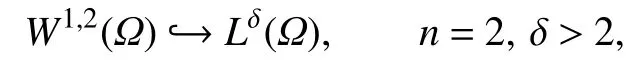
即

其中C1=(n,Ω)为依赖于n和Ω的常数.主要结论陈述如下.
定理2假设u为问题(1)的非负经典解,假设条件(2)、(3)和式(28)成立,如果问题的解在有限时刻t∗发生爆破,则有爆破时刻的下界为
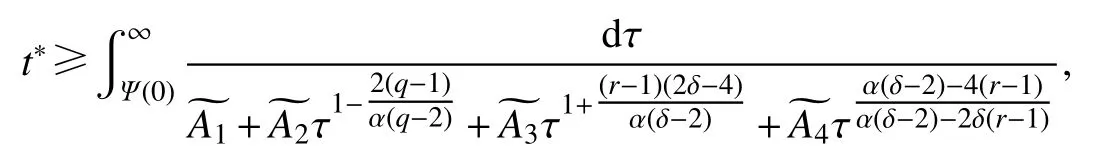
其中
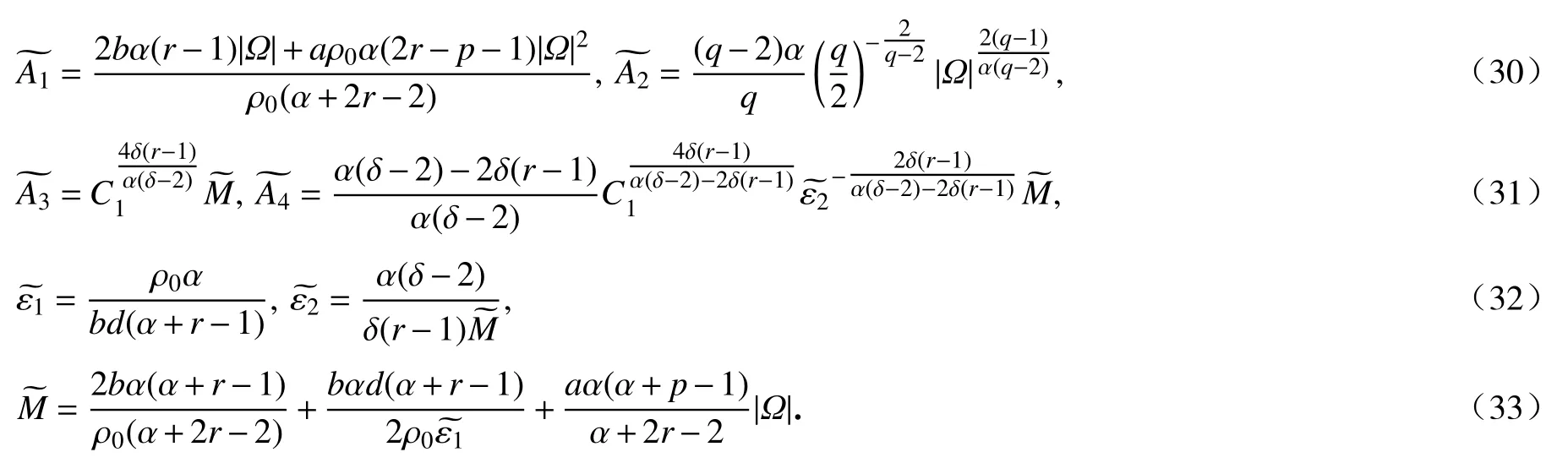
证明重复第1 节中式(10)~ (15)中的计算过程,我们有
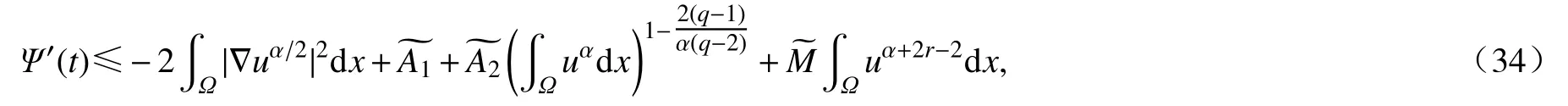
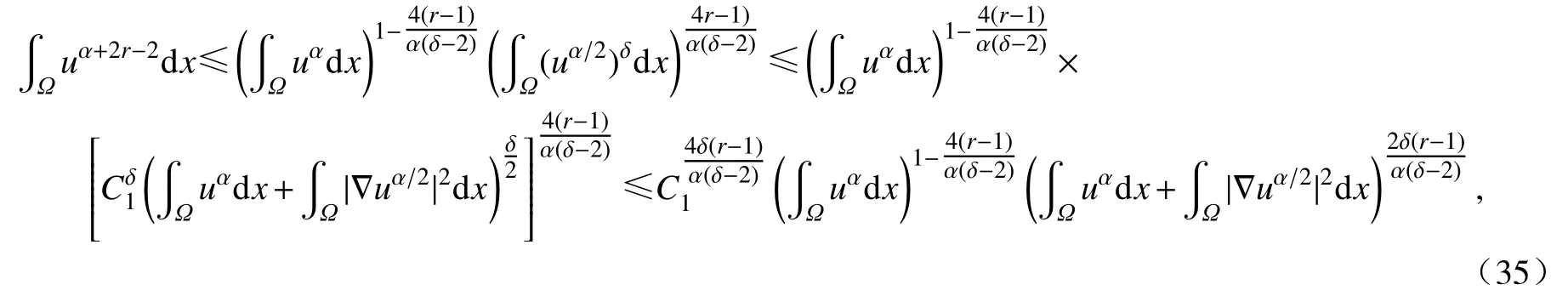

对式(36)运用Hölder 不等式和Young 不等式,有
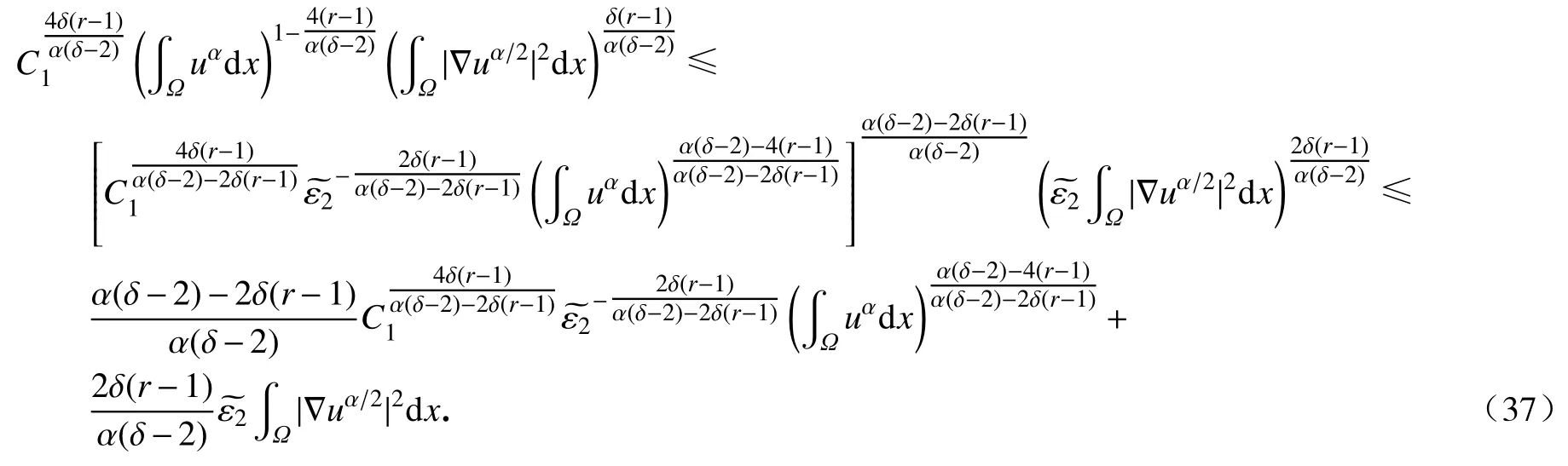
将式(35)~ (37)代入式(34),推出
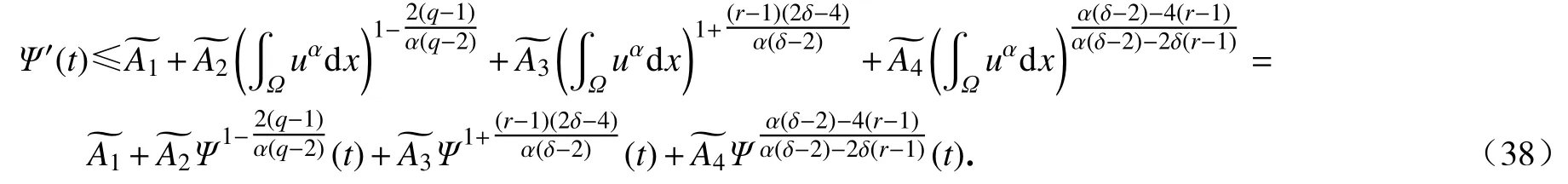
对式(38)两边从0 到t积分可得
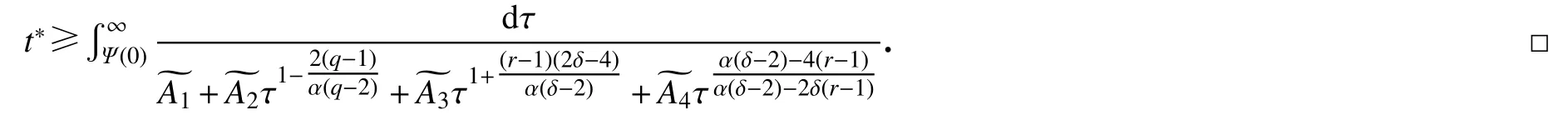
3 应 用
在本节中,我们给出具体的实例来论述文中的抽象结论.
例1令u(x,t)为下列问题的非负经典解:
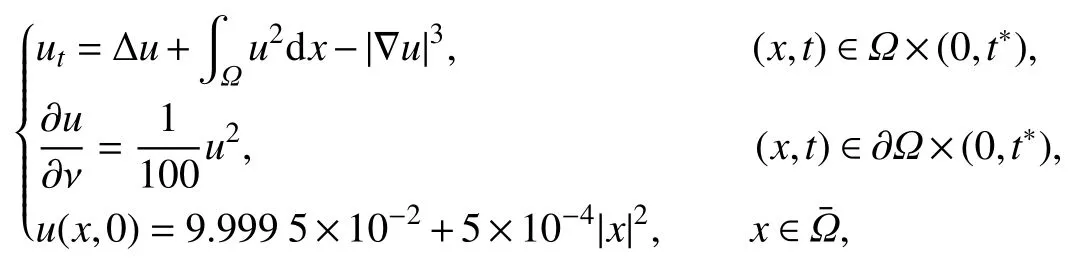
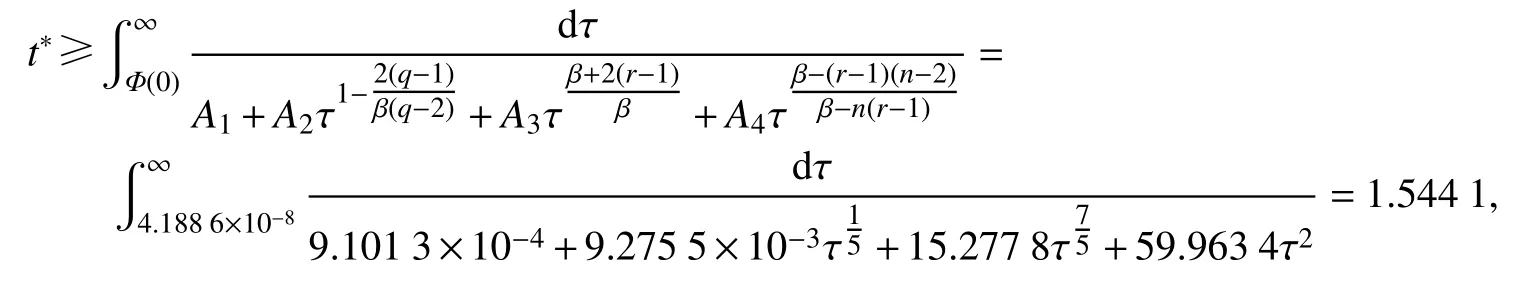
其中
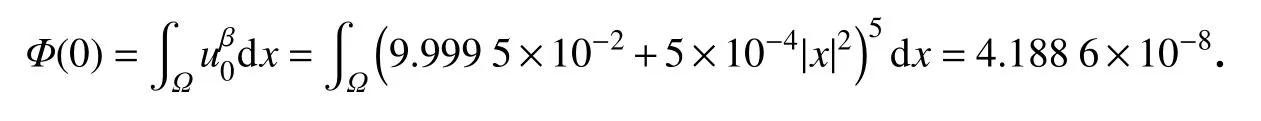
例2令u(x,t)为下面问题的非负经典解:
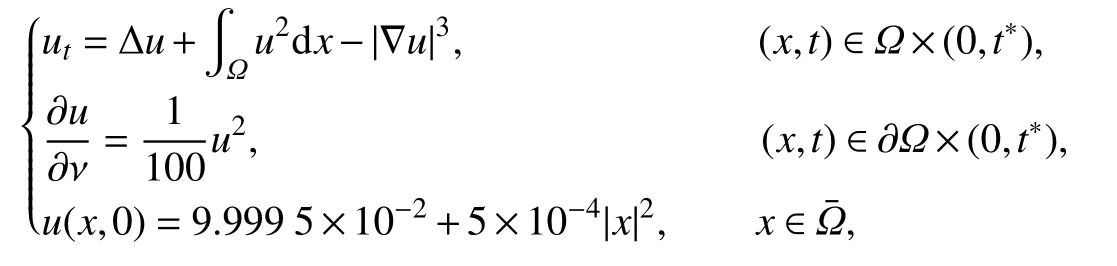
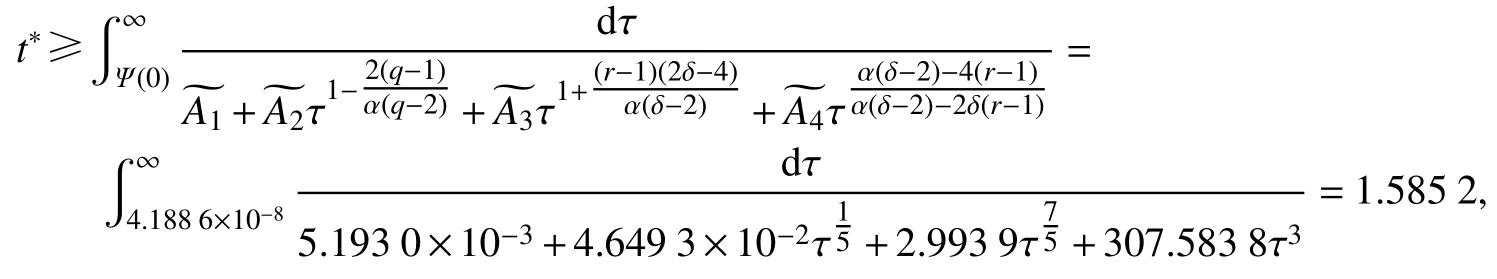
其中
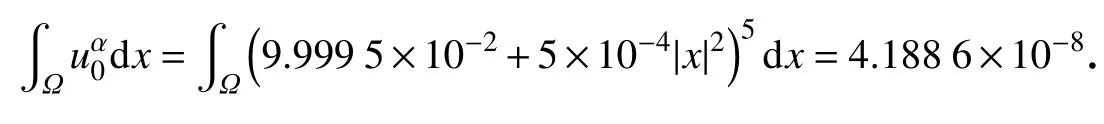
4 结 论
本文通过考虑一类带有非局部源和梯度源的反应扩散问题,通过构造合适的辅助函数,利用微分不等式技术和Sobolev 嵌入不等式,分别给出了区域 Ω ⊂Rn(n≥3)和 Ω ⊂R2上解的爆破时刻下界,并通过实例对结论进行验证.解决本文的关键是通过构造合适的辅助函数和使用Sobolev 不等式,本文的方法可为此类问题研究提供一定的借鉴.同时,关于在非线性边界条件下具有非局部源和梯度源的反应扩散问题解的爆破时刻讨论仍可开展持续的研究.

