面向贝叶斯方法的作战试验样本量估算研究*

薄 云，廖学军，白洪波，白 宇

（1.航天工程大学研究生院，北京 101416；2.中国白城兵器试验中心，吉林 白城 137001；3.航天工程大学航天保障系，北京 102206；4.国防大学联合勤务学院，北京 100039）

0 引言

贝叶斯方法作为一套重要的数据分析与决策支持框架，以知识更新的方式，融合了多种来源的信息，不仅利于减少试验的样本需求量，而且它的推理过程和推理结果比数理统计具有更加明确的概率含义，既便于理解，也便于推广应用。但贝叶斯方法需要计算非常复杂的数学期望，因此，在计算机普及之前，它的应用通常只限于基于共轭分布的有限范围。这也是自它创立以来，少有武器装备试验鉴定相关实践的原因。

作战试验是我军武器装备试验鉴定体制机制改革引入的新型试验。通过组织作战人员在模拟实战条件下“试用”被试武器装备，判断该武器装备对于既定作战任务的完成程度和适用程度，进而辅助决策是否应当大批量采购该武器装备，表现出高度实战化的特征。这一方面保证了作战和装备管理部门可以在和平环境下，以理性的方式遴选出最适用于战场的武器装备，另一方面也使得作战试验的组织过程耗资巨大、组织艰难且具有很高的危险性。因此，以尽可能少的试验次数，获取足够的辅助决策数据，即科学估算样本量，是作战试验策划中的重中之重。

考虑到贝叶斯方法在数据分析和决策支持方面的优势，且随着计算手段的不断丰富，尤其是各类马尔科夫链蒙特卡罗方法的引入，为贝叶斯方法在试验鉴定领域的广泛应用提供了可能，我军后续的作战试验也势必会增大相关应用比重，而当前的相关研究主要集中于贝叶斯方法的基本原理和应用框架的论述，比较缺乏样本量估算方面的研究，因此，本文分析了贝叶斯方法在作战试验中的两种主要应用模式，其次探讨了作战试验样本量估算的基本准则，接着根据准则分别给出了两种应用模式下的样本量估算方法步骤，最后通过算例展示了这些样本量估算方法的有效性和可拓展性，从而可为我军后续相关实践提供良好参考。

1 作战试验中的贝叶斯方法

截止目前，试验鉴定所依据的各类经典数理统计方法基本上都可以在贝叶斯方法中找到对应版本，而且在诸如可靠性这样需要融合多源信息的应用场合中，贝叶斯方法的解决方案通常要优于经典数理统计。所以，本节参照经典数理统计在作战试验中的应用情况，概述未来贝叶斯方法在作战试验中的可能应用模式，并概述相应的处理过程。

1.1 两种应用模式

当前作战试验分解武器装备作战需求形成指标体系，通过试验获取底层指标数据，以某种效能评估方法评估武器装备的作战效能和作战适用性。在此过程中，底层指标数据的获取是各层级作战效能与作战适用性评估的基础。贝叶斯方法在作战试验中的应用，也聚焦于这些底层指标，具体有两种模式。

一是推断考核指标是否达到并超过合同规定。作战试验需要对照被试武器装备的研制总要求、试验鉴定总案和具体的试验方案，对被试武器装备的大量作战效能和作战适用性指标进行考核。其基本途径就是根据实装试验数据，判断被试武器装备是否达到并超过合同规定。在这一过程中，应用的统计学工具主要是各类假设检验。

二是给出装备参数满足规定精度的数值估计。除了考核武器装备是否达到并超过研制合同规定的各项指标之外，作战试验还有可能针对武器装备未来的作战应用，或是产品型号的升级改进，而对武器装备的一些重要参数进行探索性摸底。在这一过程中，应用的统计学工具主要是区间估计。

1.2 处理过程概述

首先是推断的处理过程。如前所述，作战试验在推断武器装备的某项指标是否达到合同规定时，通常使用的统计学工具是假设检验，即根据统计法则，判断武器装备的作战试验数据是否支持指标通过考核的结论。在贝叶斯的方法框架下，可以利用贝叶斯因子开展类似的推断过程，但更直观的处理方式通常如下页图1 所示。

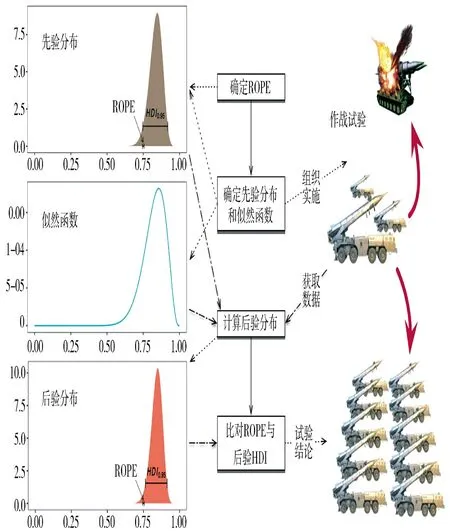
图1 基于贝叶斯方法的作战试验指标推断过程

第1 步，确定一个指标规定值的等效区间（Region of Practical Equivalence，ROPE）。例如合同规定被试武器装备的毁伤概率应大于0.75，试验中，定义该指标的ROPE 为［0.745，0.755］，即认为在实践中，从0.745 ～0.755 之间的毁伤概率和0.75 的毁伤概率并没有实质区别。

第2 步，根据武器装备性能试验或模拟仿真的结果，确定该指标的先验分布和似然函数。例如beta 分布与n 重贝努利分布的分布律。

第3 步，依据作战试验采集的实装数据，按照贝叶斯法则计算指标后验分布，并在该分布中求取指定后验概率的最高密度区间（Highest Density Interval，HDI）。例如满足95%后验概率的分布，且概率密度最高的区间范围。

第4 步，比对该HDI 是否超过ROPE，且相互不重叠。如果答案是肯定的，则认为作战试验数据支持该指标达到合同规定要求，并且该论断的正确概率大于95%。

其次是估计的计算过程。从推断的计算过程可以看出，当不考虑ROPE，仍然按照上述流程组织试验，并由后验分布计算得出的HDI 实际上就是符合特定概率要求的指标估计。

由于经典数理统计的区间估计表达的含义是在所有按照统计模型计算得出的数值区间中，有置信概率的区间包含了真实的指标值，但当前得出的置信区间是否包含指标真值却无从得知；而HDI 表达的含义是根据最新数据对于先验知识的更新，指标具有最高概率的区间即为HDI，从而更加符合一般人对于指标“置信”区间的认识，因此，从这个意义上说，HDI 对于非数据专业人士的决策辅助更加直接有效。

2 相应的样本量估算研究

2.1 估算的准则

1）基于统计功效。即假设检验备择假设为真时，正确拒绝原假设的概率。由于试验的结果受随机性的影响，并不总能真实反映被考核指标的真实情况，所以经典的数理统计和贝叶斯方法都定义了统计功效的概念，来量化试验结果对于真实情况的捕获能力。文献［12-14］论证了统计功效与结果正确性之间的交互关系，指出统计功效低下的试验会得出具有误导性的结论，并指出即使是国际顶级期刊，其发布的很多研究结论由于试验统计功效低下而可能是错误的。考虑到实施作战试验的目的是通过考核武器装备决策是否大批量采购并部署武器装备，所以它的结论的正确性关系到战争的胜败和战士的生死。因此，考虑面向贝叶斯方法的作战试验样本量的估算问题时，也应当把满足统计功效作为选取样本量的客观标准。

2）区分应用模式。经典数理统计的统计功效被定义为原假设不真实时，正确拒绝原假设的概率。而在贝叶斯的方法框架下，需要区分具体的应用是上述的推断问题还是估计问题。

对于面向推断的贝叶斯方法来说，它的统计功效实际上是在给定先验信息和似然函数的前提下，后验HDI 可以超出ROPE 并不与其相交的概率。

对于面向估计的贝叶斯方法来说，它的统计功效则是在给定先验信息和似然函数的前提下，后验HDI 的宽度小于指定精度要求的概率。

3）投入最少原则。一般来说，可以通过3 个因素提升特定试验的统计功效，①降低试验的干扰因素影响；②提升数据采集的精度；③增加样本量。由于前两个因素在试验开始前已经固定，所以只能通过第3 条途径，也就是通过增加样本量提升试验的统计功效。而作战试验耗资巨大，且具有一定的危险性，所以在试验具有一定的统计功效，可以确保数据质量的前提下，应当遵从投入最小原则，即样本量应当尽可能地小。

2.2 估算的方法步骤

第1 步，根据性能试验、仿真试验、甚至是类似装备的已有数据，确定待考核指标的验前分布。

第2 步，根据被试装备的最新状态，估计待考核指标各生成参数的概率分布。

第3 步，由这些参数的概率分布，生成N 组参数的随机值，再由每组参数的随机值生成s 个该考核指标的模拟值。

第4 步，把这些模拟值当做实际采集的装备数据，结合第一步确定的先验分布，利用贝叶斯法则，计算指标的后验分布。如果这其中有n 个后验分布达成目标，则该试验的统计功效约为β=n/N。

第5 步，判断该统计功效是否达到要求，如没有，则令s=s+1，返回第3 步，直至统计功效达到要求，此时的s 即为所求的样本量。

3 算例演示

通过前述可以看出，作战试验中基于贝叶斯方法的考核在进行样本量估算时，主要是利用仿真，模拟作战试验的数据采集过程，然后通过分析这些仿真结果来估算考核的统计功效，并令能够达到统计功效要求的最小样本量为所求的样本量。同样，这里的样本量计算也需要区分考核是基于贝叶斯方法的推断问题还是估计问题。

3.1 针对统计推断的样本量估算演示

假设研制总要求规定某型卫星通信终端通话质量的满意度大于80%，则估算过程如下：

第1 步：定义为满意度水平，利用性能试验、仿真试验的已有数据，确定待考核指标的验前分布为服从形状参数为106 与19 的beta 分布。

第2 步：通过该型卫星通信终端性能改进的最新情况，估计生成的概率分布的众数Omega 和聚集参数Kappa 分别服从形状参数为96、6 的beta 分布和形状参数为2 000 、尺度参数为1 的gamma 分布，而实际生成的作战试验数据服从以p 为参数，以样本量s 为规模的二项分布。

第3 步：由第2 步估计的各分布模拟生成试验数据。通过观察图2 左上角的分图，发现当模拟次数达到3 000 次时，仿真结果基本完成收敛，仅在很小的范围内上下波动。因此，样本量估算的数据分析皆基于3 000 次仿真模拟的试验数据。

第4 步：结合以上信息，利用贝叶斯法则，计算后验分布，并求得在各样本量水平s 下每次仿真结果的HDI。

第5 步：统计各样本量水平s 下3 000 个HDI超出ROPE 的比例，即为该样本量水平下的统计功效，得到如图2 右上角分图所示的统计功效变化趋势图。可以看出，当s≥23 时，统计功效大于0.80，即在0.8 的统计功效水平要求下，试验的样本量应取23。

3.2 针对统计推断的样本量估算演示

假设研制总要求规定在某型卫星通信终端的试验中获得通话质量小于0.1 精度水平的满意度估计，则样本量的估算过程如下：

第1 步～第4 步仍然同上。

将第5 步调整为：统计各样本量水平s 下3 000个HDI 的长度小于规定精度要求的比例，即为该样本量水平下的统计功效，如图2 左下角分图所示，进而分析可得如图2 右下角分图所示的统计功效变化趋势图。可以看出，当s≥48 时，统计功效大于0.80，即在0.8 的统计功效水平要求下，试验的样本量应取48。

3.3 应用估算方法的特殊问题

一是仿真结果收敛性对样本量估算的影响。本文的样本量估算方法是基于仿真的，必定存在随机性，为获得相对正确的样本量估算结果，应当确保仿真结果可收敛。即随着仿真步数的增加，仿真结果逐渐收缩至一个相对较小范围。如果通过观察，发现仿真结果不具备收敛性，则需要判断无法收敛的原因是该仿真模拟的数据生成过程与实际情况不符，还是实际上即将开展的试验永远无法达到规定的统计功效水平。通过观察图2 的左上分图可以看出，在仿真结果可收敛的情况下，仿真的步数越多，结果变化的震荡幅度越小，并逐渐收敛至真实值附近，但仿真的步数越多，计算的开销越大，因此，在实际的样本量估算过程中，应当选择合适的仿真步数。

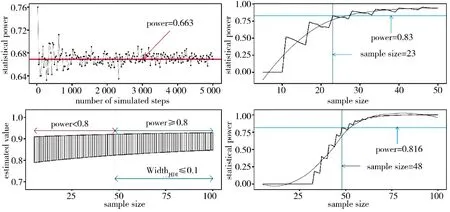
图2 算法有效性验证示意图

二是试验结果计算过程对样本量估算的影响。本文给出的算例相对较为简单，它们用到的先验和似然分别为beta 分布和二项分布的分布律，而beta分布和二项分布互为共轭，即利用传统的解析方法完全可以基于统计功效估算样本量。然而当前试验鉴定应用贝叶斯方法的主要场景是诸如可靠性指标考核这样需要融入大量先验信息的情况，几乎无法使用解析方法计算试验结果，必须利用马尔科夫链蒙特卡洛这样的仿真方法计算试验结果。但通过分析本文提出的样本量计算过程可以看出，在利用统计功效作为估算法则的前提下，只需要试验结果的计算方法可生成后验分布即可，并不区分它是利用解析方法，还是仿真方法。因此，本文提出的样本量估算方法，可以推广至基于贝叶斯方法开展的可靠性考核等复杂场景。

三是更多决策因素对样本量估算的影响。本文提出的样本量估算方法是以统计功效作为判断标准的，即主要考虑样本量的选择能否满足试验的数据质量要求。但在实际的试验工作中，常常还需要考虑试验资金、日程安排、实施可行性等更多方面因素。这实际上是在样本量的估算问题中引入了更多的约束条件。因此，如果实际的试验工作确实需要考虑这些约束条件，还需要进一步利用最优化的规划方法，计算得出一个试验样本量的满意解。

4 结论

通过分析当前作战试验应用贝叶斯方法的现状，本文指出主要有指标推断和指标估计两大类的应用场景，在讨论了样本量估算的准则之后，分别给出这两类应用场景下的样本量估算步骤。通过算例的演示和方法应用的讨论，可以看出，本文提出的方法是具有一定的通用性，基本可以覆盖当前作战试验基于贝叶斯方法考核的样本量估算需求，因此，可以为我军后续的相关试验鉴定任务实践提供较好的参考。