基于GMS的抗浮设防水位研究——以合肥市轨道交通工程地下车站为例

赵燕容,张子民,董小松,陈 健,卢 刚

(1.河海大学地球科学与工程学院,江苏 南京 211100; 2.安徽省城建设计研究总院股份有限公司,安徽 合肥 230051)

当前,关于抗浮设防水位的研究越来越受到重视,当地下水上浮力大于建筑荷载时,往往引起建筑结构破坏从而导致事故的发生。1928年美国旧金山市圣弗兰西斯大坝发生的溃坝事故使人们首次认识到了地下水浮力的危害;1995年北京官厅水库泄洪导致下游地区建筑地下室开裂,从此我国开始系统地研究抗浮问题[1];2014年毕节市某医院地下车库部分梁、板、柱在雨后发生裂变;2020年南昌市某小区降雨后地下车库发生局部上浮事件,车库多个结构被破坏。随着对地下空间的开发,建筑物地下室的数量和深度不断增加,抗浮设防将成为一个常见的技术问题,地铁工程因埋深大更易受到地下水浮力的危害,如2011年南京地铁2号线车站路基被地下水抬升约20 cm,造成地铁停运。因此,在抗浮设防工作中得到准确的抗浮设防水位具有重要意义。目前,由于水文地质条件的复杂性,水文地质勘察工作很难提供足够精确的抗浮设防水位。

抗浮设防水位是指建筑在各种不利工况组合下,设计使用年限内可能产生的最高地下水位,实际工程中一般使用勘察期间场地历史最高水位作为抗浮设防水位,但因很多地区缺乏历史资料,需要综合各种技术手段来研究和确定抗浮设防水位。李永彪等[2]通过对地下水动态的监测,运用动态曲线比拟法预测了合肥地铁抗浮水位;蔡海艳[3]以乌鲁木齐市地铁为例,详细阐述了影响抗浮设防水位的各种因素(如侧向径流和降雨入渗),最终以数值模拟计算得到抗浮设防水位;刘建豹等[4]基于水文地质调查方法,在查明地下水补径排条件、季节动态变幅后确定了济南某大厦的抗浮设防水位;叶树人[5]提出考虑到建筑物地基的渗透性,可按照一定的折减系数乘以历史最高水位得到抗浮设计水位;段平国等[6]认为如果场地与周围道路形成一定高差,抗浮设防水位可以按照室外道路标高确定;刘国亮等[7]通过研究天津市区地下水抗浮设防水位,提出应将场地的地貌情况、地质条件和建筑物情况综合分析,使用最不利组合的方法确定抗浮设防水位。综上所述,目前对于如何确定抗浮设防水位没有统一且明确的方法,并且各地设防水位的取值存在一定差异,通用性差。若取值过高会增加建设成本,取值过低则会留下安全隐患,因此如何综合考虑各影响因素并准确确定抗浮设防水位仍是施工设计中面临的重难点问题。

以合肥市轨道交通工程车站为研究对象,构建地下水渗流三维数值模型,对研究区抗浮设防水位展开研究。通过搜集合肥市多年气象资料以及地下水监测资料,利用GMS数值模拟软件及其 MODFLOW-USG模块建立渗流模型,对构建的地下水渗流模型进行识别与验证,数值模拟预测得到的最高地下水位可为地铁车站工程抗浮设防水位设计提供依据。

1 研究区概况

1.1 工程概况

合肥拟建轨道工程包括8号线1期、7号线与S1号线,其中8号线1期北起北城高铁站,南至阜阳路站,解决了北城与中心城区之间联系的迫切需要;7号线西起松林路站,东至巢湖南路站,增强了滨湖中心对外辐射功能;S1号线西起新桥机场,向东止于广东路站,连接了新桥机场、新合肥西站、南站城际站三大交通枢纽。8号线1期、7号线与S1号线车站位置见图1。研究区内地势总体由西北向东南倾斜,地形以丘陵、波状平原为主,毗连巢湖,平均海拔为20～40 m,地形相对平缓。3条线路共有48座地下车站,其中8号线1期13座地下车站,全线共24.8 km;7号线17座地下车站,全线共18.8 km;S1号线18座地下车站,全线共45.9 km。

1.2 水文与气象

巢湖及其水系位于研究区南部,瓦布湖、高唐湖及其水系位于研究区北部。这一地区的河流以江淮分水岭为界,南有长江水系,北有淮河水系,前者由南淝河、派河、店埠河、滁河组成,后者包括东淝河、沛河和池河。研究区内河流集水面积小,详细水系分布如图2所示。

据以往资料显示,合肥市的降水较充足,年平均降水量为994.9 mm。5—9月易出现暴雨,占年降水量的3/5。1954年降水量最大,约1 541.9 mm;1978年降水量最小,约546.2 mm。数据显示,7月份是全年降水量最多的月份,平均为173.9 mm;12月是降水量最少的月份,平均降水量为28.2 mm。年平均蒸发量835 mm,6—8月温度最高,蒸发最强;12月—次年2月温度最低,蒸发较弱。

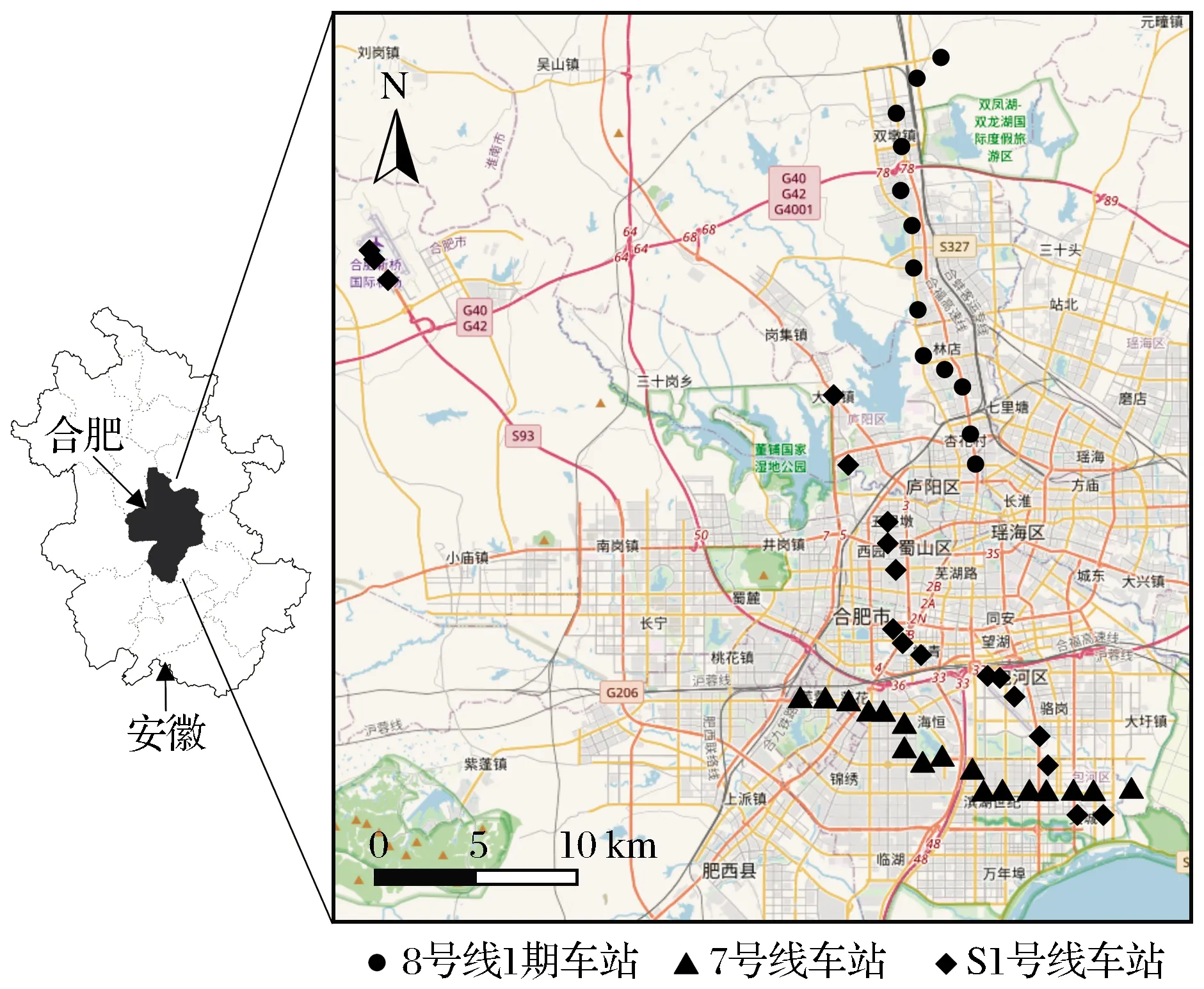
图1 地铁车站分布Fig.1 Distribution of subway stations

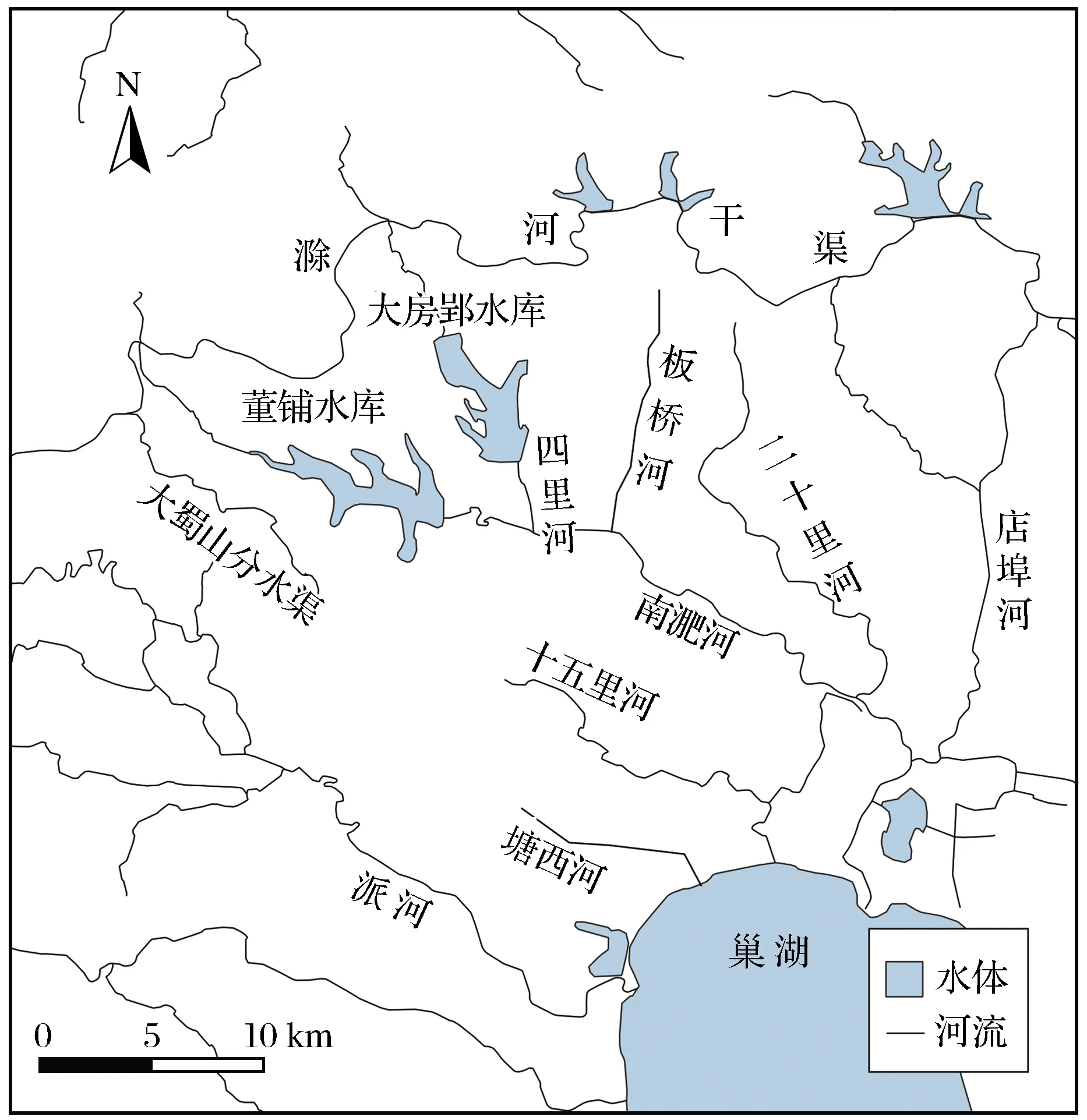
图2 研究区水系Fig.2 Water system of the study area

1.3 地层岩性

合肥市境内大部分为第四系松散沉积物覆盖,主要为第四系人工填土、第四系全新统南淝河组粉质黏土、上更新统下蜀组粉质黏土、残积层粉质黏土,其在波状平原区厚度为5～50 m,在冲击平原厚度为15～60 m,第四系地层厚度从西北丘陵至巢湖平原逐渐增加。下伏基岩主要为第三系定远群和白垩系张桥组泥质砂岩、砂岩及砂质泥岩、泥岩,基岩顶板埋深在10～40 m,其中城区西北、西部及西南基岩顶板埋深为10～20 m,城区北部、东部及东南部基岩顶板埋深为25～40 m,最大可达50 m以上。

1.4 水文地质条件

合肥市地下水主要由上层滞水、松散岩类孔隙水和基岩裂隙水组成。回填层内分布有上层滞水,但其分布不连续,埋深一般在自然地表以下5 m内。第四系的松散岩类孔隙水分为潜水和弱承压水两类,潜水主要位于上更新统黏性土中,大气降水是其主要的供水和补给来源,含水量小;弱承压水主要存在于粉土及砂土中,侧向径流是其主要补给来源,主要赋存于一、二级阶地下古河道中的粉土、粉土夹砂、粉细砂层。基岩裂隙水赋存于第三系与白垩系泥质砂岩、泥岩强～中风化层中,基岩裂隙水发育具非均一性,富水性弱,水量贫乏,具有承压性。大蜀山分布着岩浆岩裂隙含水岩组,但其水量很少。

2 地下水渗流数值模型的建立与识别校准

2.1 数学模型

根据地下水渗流连续性方程,在研究区非均质各项同性含水层建立的地下水非稳定流三维数学模型为

(1)

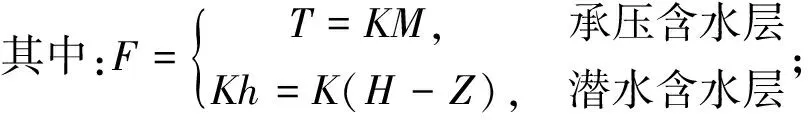
h为地下水位(m);h0为含水层初始水位(m);q为单位面积过水断面的流量(m/d);W为源汇项(m/d);Γ1和Γ2分别表示第一类、第二类边界条件;Ω代表研究区;T为导水系数(m2/d);K为渗透系数(m/d);M为承压含水层厚度(m);H为潜水面高程(m);Z为潜水含水层底板高程(m);μ为重力给水度;μ*为弹性贮水系数。

2.2 水文地质模型概化

(1) 含水层概化 地铁深度影响范围内的地下水包括上层滞水、潜水与承压水,局部存在的上层滞水没有固定的自由面,虽然其在小范围集中产生的自由面也会产生浮力,但因地铁车站埋深大,上层滞水并没有直接作用于建筑基低,所以潜水与承压水对抗浮起主导作用。根据水文地质条件,可将研究区含水层概化为2层:第1层为潜水含水层,其主要由粉土、粉细砂、粉质黏土组成,厚度在10～25 m之间;第2层为承压含水层,其由下伏风化残积层组成,两层之间的隔水层由GMS的confining bed模块模拟。

(2) 边界条件概化 根据合肥市水文地质图,将江淮分水岭确定为研究区北界,概化为隔水边界,东南部边界为店埠河,概化为变水头边界,东北部边界与地下水流线平行,概化为隔水边界;南部边界受巢湖影响,概化为变水头边界,西北部边界与地下水流线平行,概化为隔水边界;西南部边界是派河,概化为变水头边界,模型第二层侧向边界概化为定水头边界。合肥地区河流与地下水系统水力联系良好,河流可以设置为变水头边界,收集各河水位观测点数据,插值得到河流水头变化值。研究区内有两座水库:董铺水库与大房郢水库,因模拟运行期间水库的水位变化不大而水库面积较大,水库边界设定为定水头边界,董铺水库水头设置为水库多年平均水位24.02 m,大房郢水库水头设置为水库多年平均水位18 m。计算模型边界条件如图3所示。

2.3 模型构建与网格剖分

研究区南北长49 064 m,东西宽50 194 m,总面积约为1 645 km2。共收集有229个勘察钻孔数据,钻孔分布如图4所示,利用GMS中Boreholes模块构建三维模型,如图5所示。模型的网格大小决定了其水力特征和应力变化能力,若网格尺寸过大,可能会遗漏地下水系统的特征,因此将平面上单元网格设置为500 m×500 m,使用U-Grid进行网格剖分,共剖分网格13 324个,节点20 625个,在垂直方向上共划分为2层。三维模型坐标为笛卡尔坐标系,x轴为正东方向,y轴为正北方向,z轴为竖直向上。

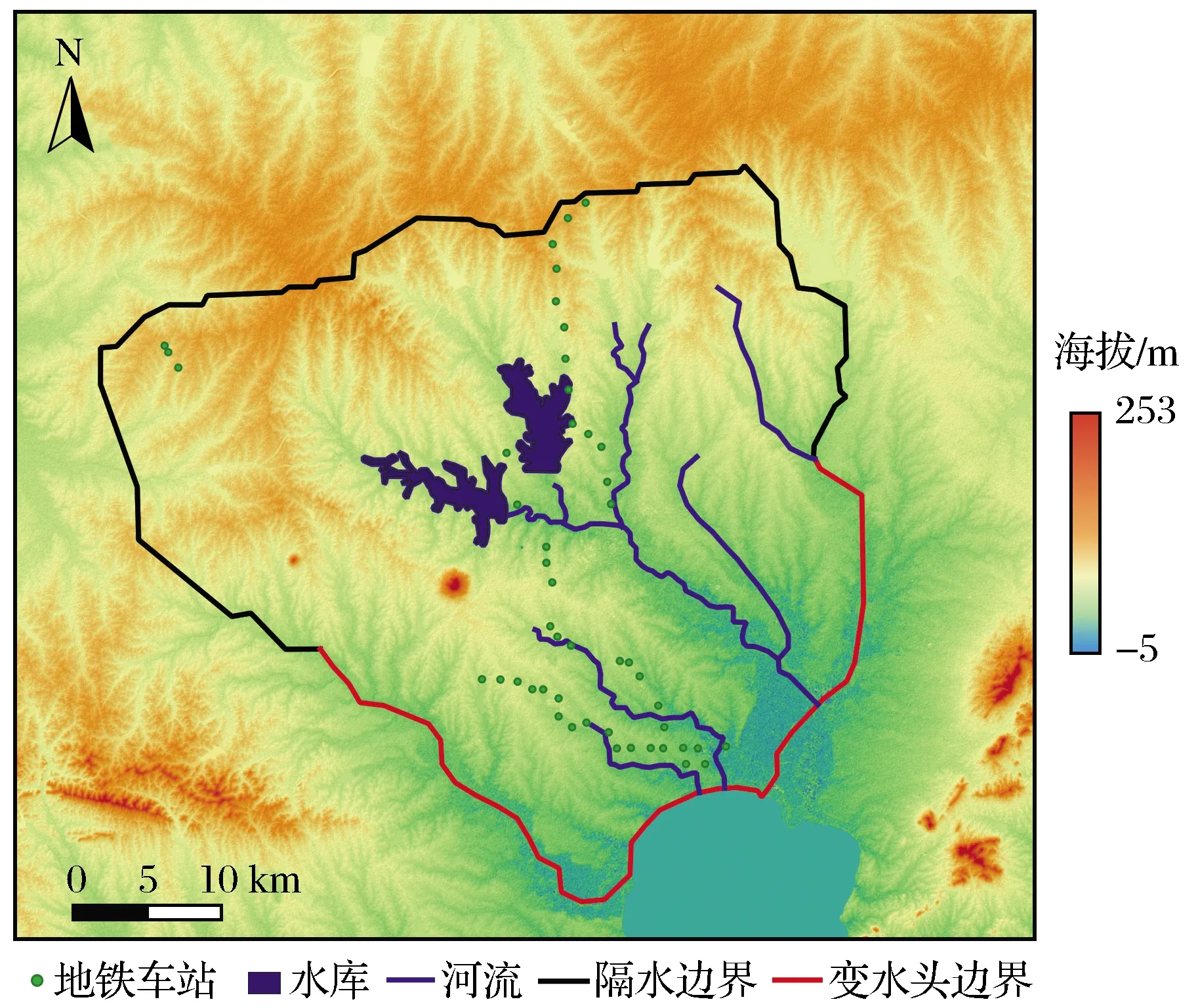
图3 边界条件示意图Fig.3 Schematic diagram of boundary conditions

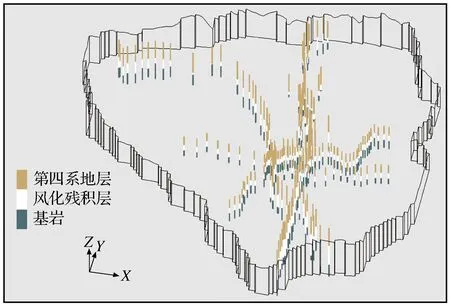
图4 研究区钻孔分布Fig.4 Borehole distribution of the study area

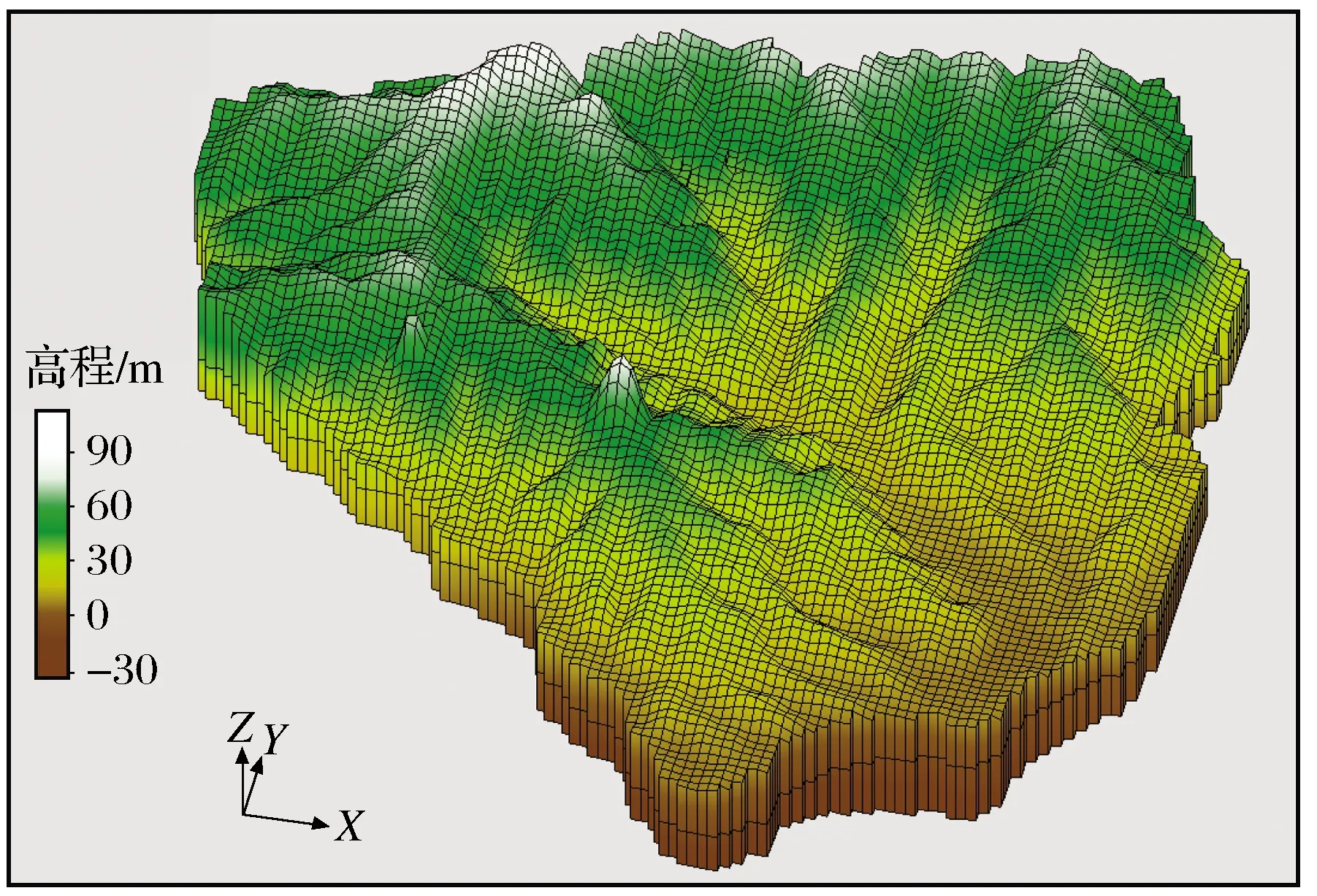
图5 三维地层模型Fig.5 3D stratigraphic model

2.4 水文地质参数分区

建立模型所需参数有渗透系数、给水度和贮水系数,其准确性直接影响模型的可靠性和可信度。通过查阅大量资料,结合勘察单位提供的区域水文地质条件和水文地质试验成果,确定了研究区的水文地质参数分区,各层的渗透系数、给水度、贮水系数见表1和表2,参数分区见图6。

2.5 初始流场

根据研究区长观井实测水位资料与边界条件,建立稳定流模型计算得出初始流场。对比稳定流模型计算与观测值插值得到的初始流场,得出稳定流模型计算结果更加精确,并且通过稳定流计算也验证了模型边界条件符合研究区的实际情况[8],研究区初始流场如图7所示。

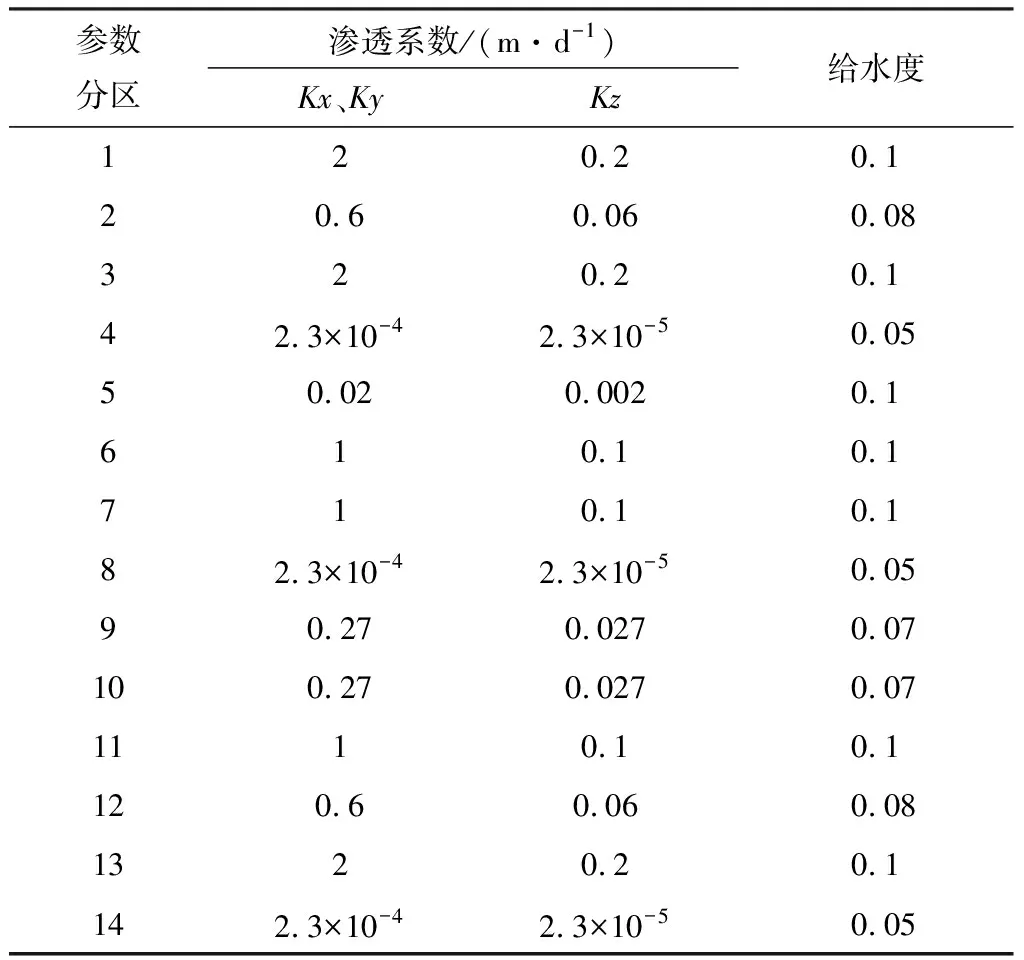
表1 潜水含水层水文地质参数Table 1 Hydrogeological parameters of phreatic aquifer

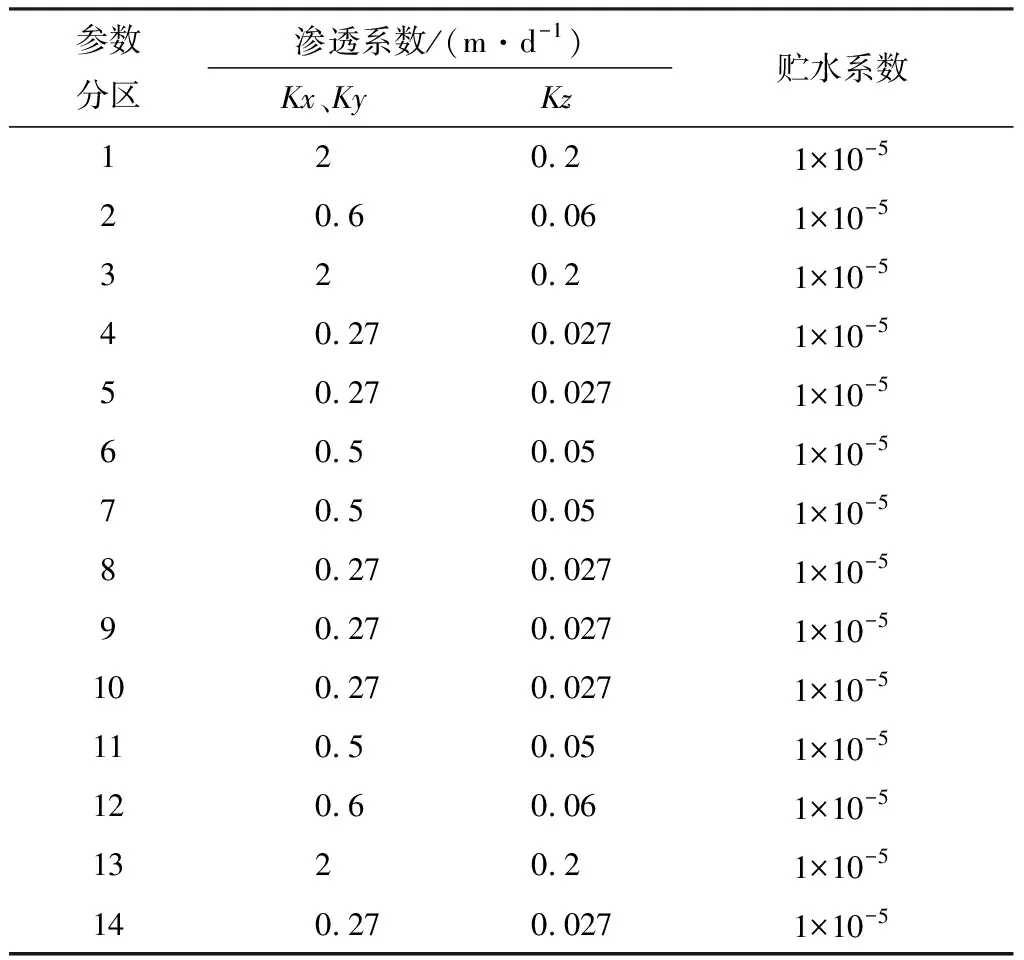
表2 承压含水层水文地质参数Table 2 Hydrogeological parameters of confined aquifer

2.6 源汇项

(1) 潜水蒸发 影响潜水蒸发的主要因素是水面蒸发量、潜水埋深与包气带岩性。潜水蒸发计算公式为

(2)

其中:ε为区域平均潜水蒸发量;ε0为区域平均水面蒸发量;Δ为区域平均地下水埋深(m),查询合肥地下水动态年报取平均地下水埋深为2.88 m;Δ0为潜水停止蒸发时的埋深(m),取5 m;n为与包气带土壤质量和气候相关的指标,一般取2。根据研究区平均水面蒸发量数据计算得出研究区平均潜水蒸发量,如图8所示[9]。

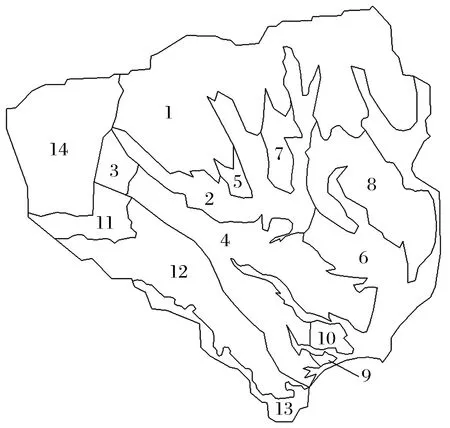
图6 研究区参数分区Fig.6 Parameter partitioning of the study area

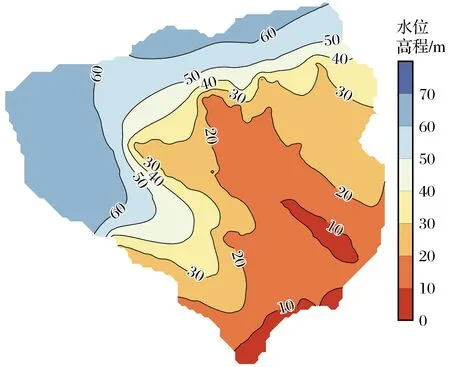
图7 研究区初始流场Fig.7 Initial flow field of the study area

(2) 降水入渗 通过对合肥市土地利用现状的分析,收集整理近年的降水资料,根据地面硬化情况将研究区划分为2个区域,硬化分区如图9所示,研究区多年平均降水量如图10所示。参考地质矿产部1985年批准的参数值(取值范围0.07～0.3),将城镇硬化区的降水入渗系数设为0.07,非硬化区的降水入渗系数设为0.1,降水入渗量的计算公式为

Q=αP,

(3)

其中:Q为降水入渗量(mm);P为降水量(mm);α为降水入渗系数。计算得出的降水入渗量将以面状补给的方式分配到各个区域,再赋值到每一个应力期。

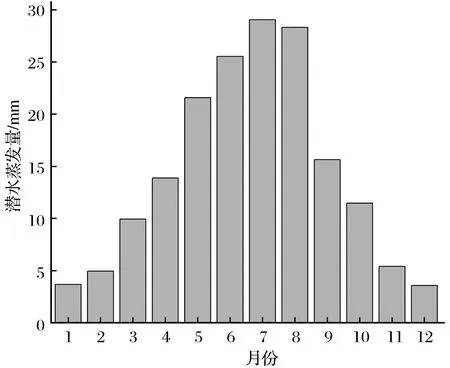
图8 研究区平均潜水蒸发量Fig.8 Average phreatic evaporation in the study area

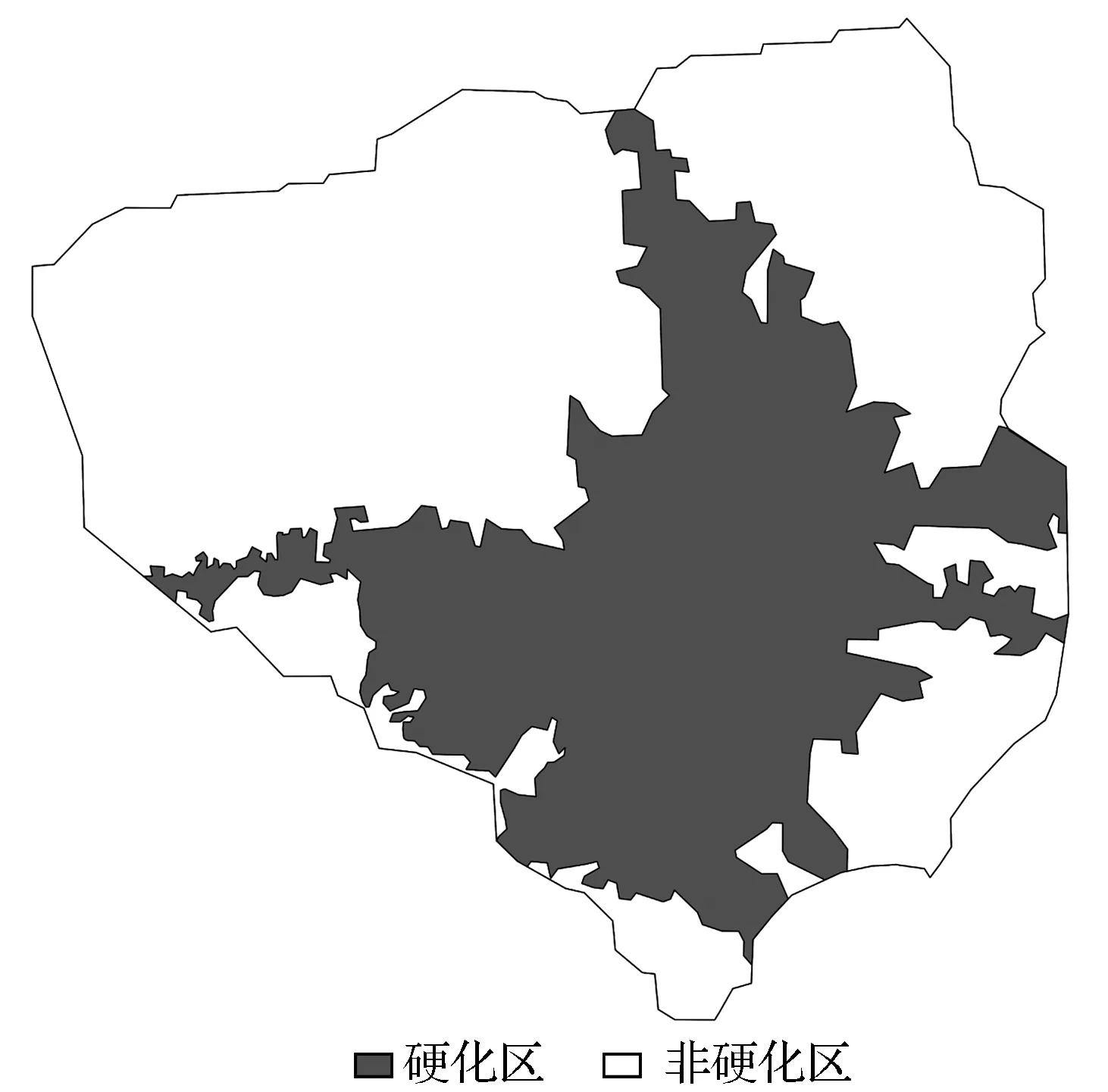
图9 硬化分区Fig.9 Ground hardening partitioning

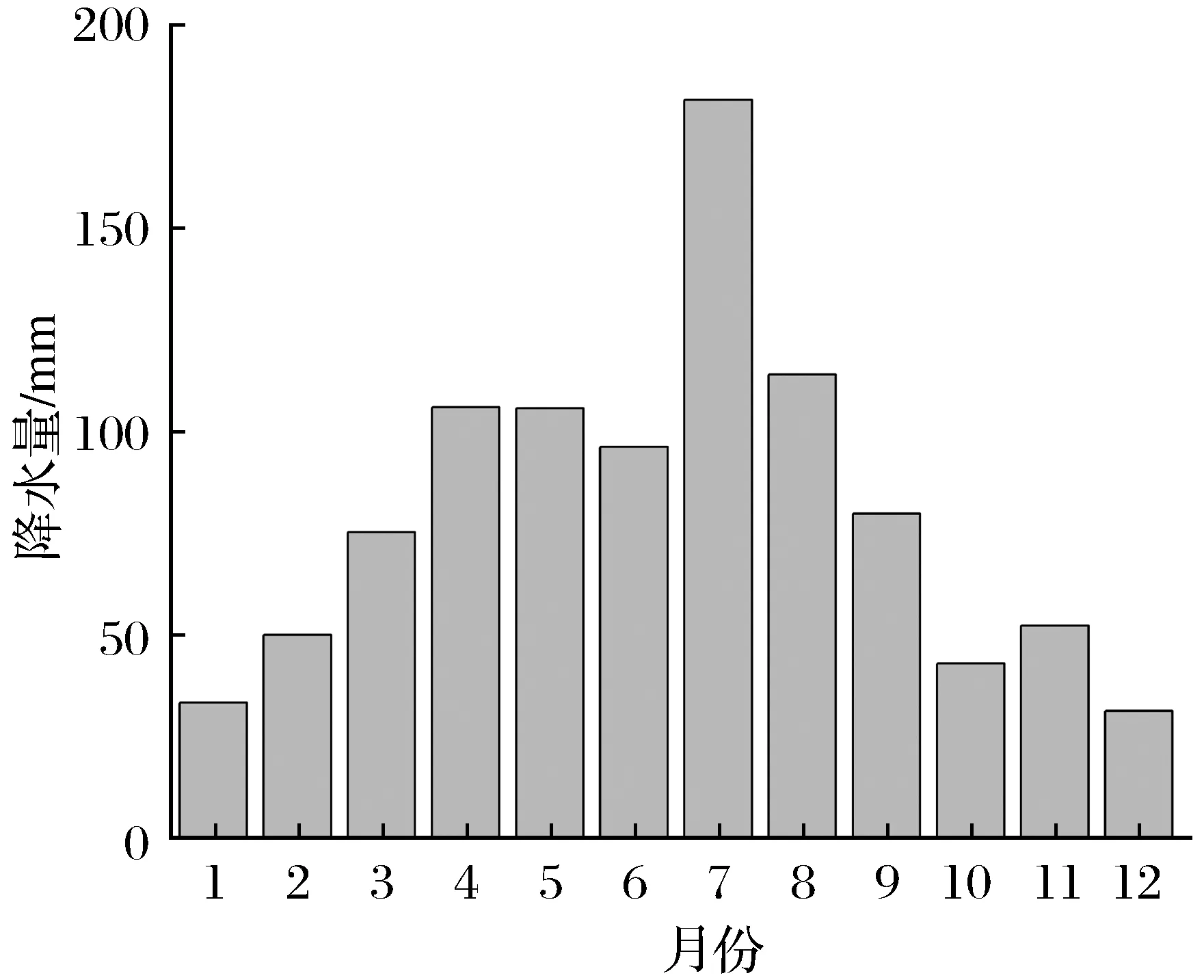
图10 研究区多年平均降水量Fig.10 Average precipitation in the study area for many years

2.7 时间离散

全部模拟拟合时间可以划分为数个应力期,同一个应力期内源汇强度不变;一个应力期还可以划分为数个时间段,其中每个时间段称为时间步长。根据地下水位观测资料,模拟期设置为2019年4月—2021年3月,以每个自然月为应力期,总共2年,每月时间步长为当月天数。

2.8 模型的识别与验证

模型识别:识别时间段为2019年4月—2020年3月,对比计算值与观测井实测水位值,利用GMS软件中的PEST模块对各参数进行优化。PEST有2种方法:先导点法与参数区块法,使用先导点求渗透系数最优值,通过参数区块法求蒸发最优值。2次调参使得计算值与观测值逐渐接近。

模型验证:验证时间段为2020年4月—2021年3月,为进一步验证所建立的数学模型和模型识别后水文地质参数的可靠性,在研究区中选择了6口具有代表性的观测井,观测值与计算值的拟合情况如图11所示。观测值越靠近计算值曲线,则误差越小,说明拟合效果好。模型验证的结果显示校准后的模型精度高,能够反映研究区真实的地下水动态变化,水文地质条件的概化具有代表性,数学模型也适合于研究区。

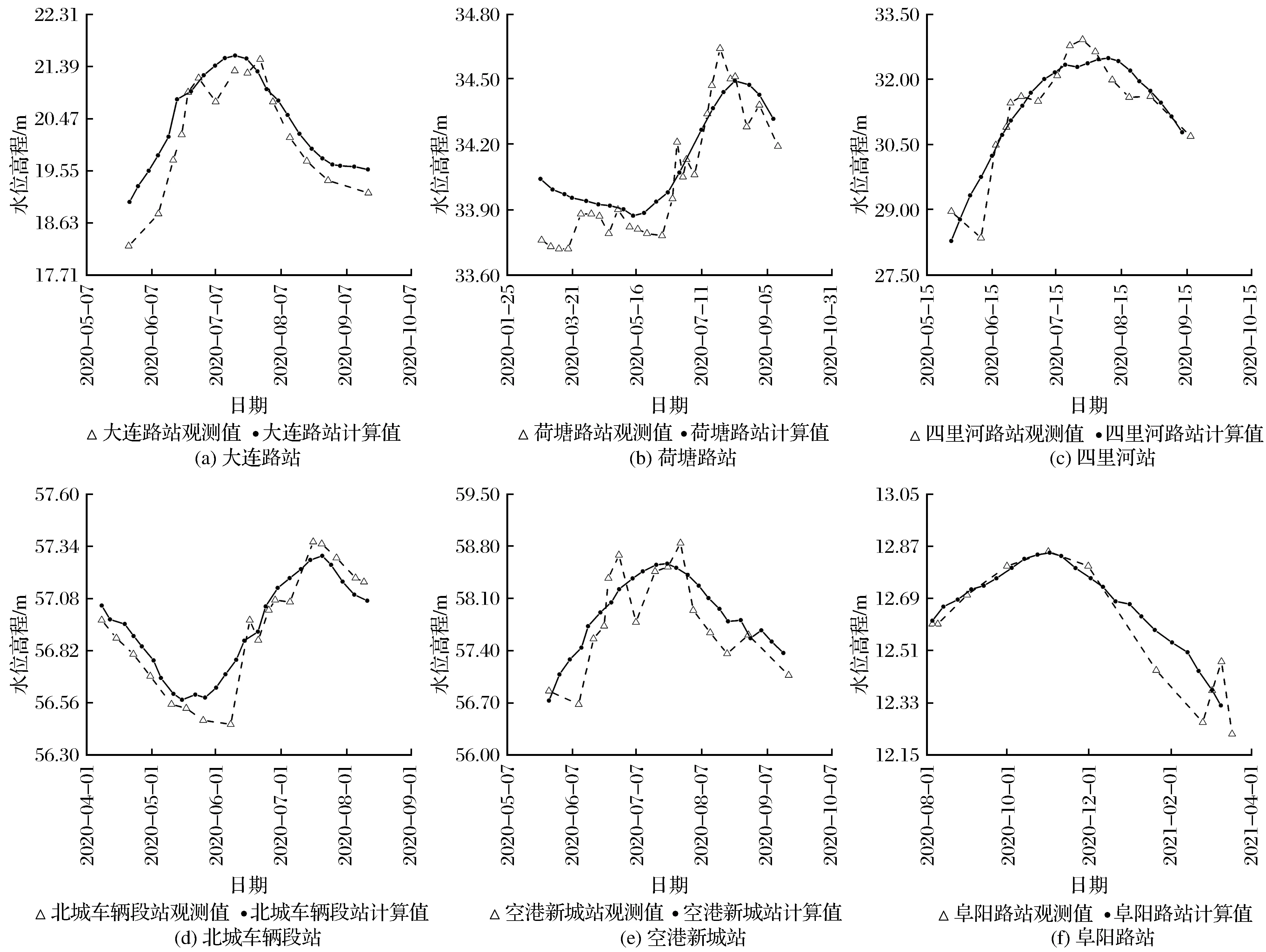
图11 研究区观测井观测值与计算值对比Fig.11 Comparison of the observed and calculated values of observation wells in the study area

3 各车站最高地下水位及抗浮设防水位的确定

3.1 百年一遇降水的确定

以1951—2019年合肥市降水统计数据为基础,使用水文频率程序绘制出P-Ⅲ型频率曲线[10],如图12所示,得出合肥市百年一遇降水量(P=1%)为1 560.6 mm。随后选择一个降水量接近1 560.6 mm的年份作为典型年,用于分配每月的降水量。最终选择1954年作为典型年,其降水分布如图13所示。

3.2 抗浮设防水位的确定

将百年一遇降水数据输入模型,其余边界条件保持不变,在此基础上模型运行一年,研究区各车站最高地下水位变化如图14所示。图14中S1号线四里河路站、固镇路站、8号线1期中段大部分站点位于丘陵与山前,地形起伏坡降大,大部分降水以径流排泄,接近四里河、板桥河、大房郢水库、董铺水库等排泄区的站点地下水位涨幅小,相比历史最高地下水位抬升0～0.7 m;8号线1期北城车辆段站、北城高铁站与S1号线新桥机场站、T2航站楼站、空港新城站均位于非硬化区,降水入渗较大导致地下水位涨幅较大,相比历史最高地下水位抬升1.2～3 m;7号线松林路站～徽富路站、S1号线史河路站～扬子江路站位于十五里河、塘西河二级阶地,阶地表层主要为极微透水性～弱透水的黏性土层覆盖,渗透性差,地下水排泄困难,地下水位涨幅大,相比历史最高地下水位抬升1～5 m;7号线上海路站～巢湖南路站、S1号线中山路站、广东路站位于十五里河河漫滩及一级阶地,地形平缓,孔隙发育,含水层渗透性好,靠近巢湖地下水排泄条件好,相比历史最高地下水位抬升1～2 m。

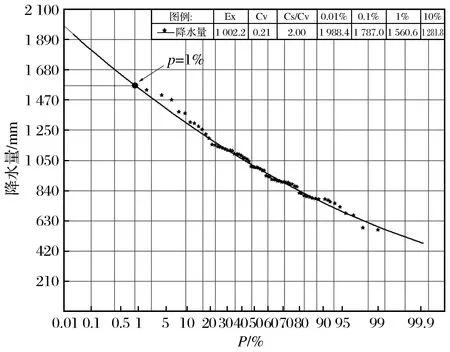
图12 P-Ⅲ型降水量频率曲线Fig.12 Frequency curve of P-Ⅲ precipitation

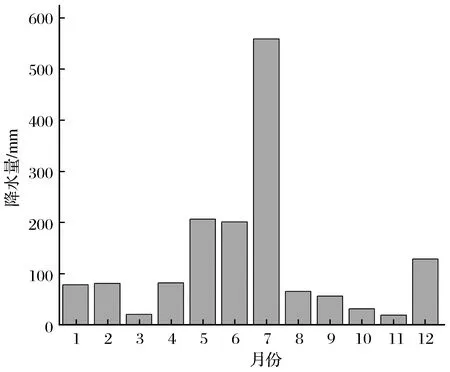
图13 研究区1954年降水量Fig.13 Precipitation in 1954 in the study area

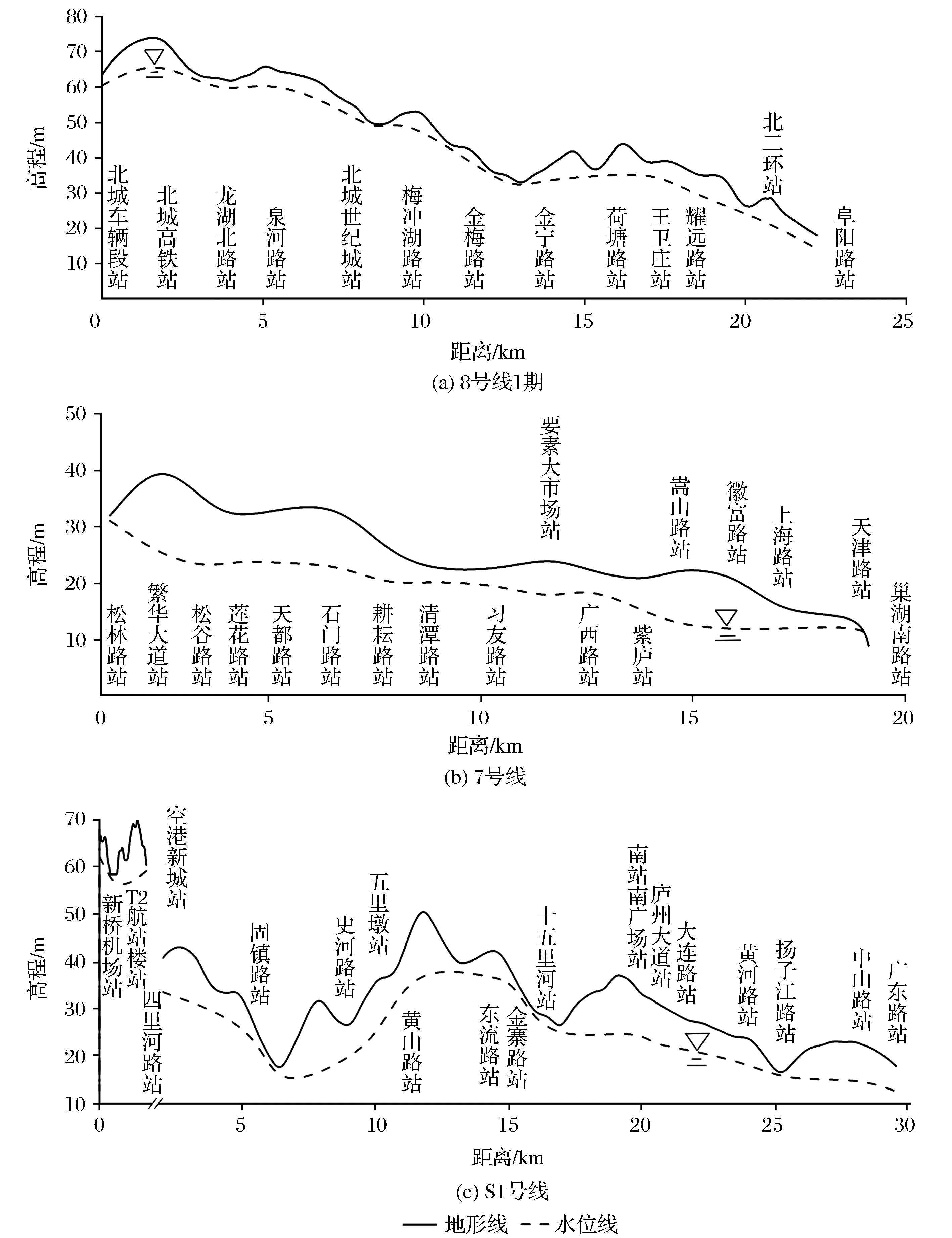
图14 8号线1期、7号线、S1号线各车站百年一遇降水条件下最高地下水位Fig.14 The highest ground water level in the 100-year rainfall condition at each station of Phase 1 of Line 8,Line 7 and Line S1

综合考虑研究区历史地下水位变幅、各车站所在场地的地层情况与数值模拟的结果,并结合《建筑工程抗浮技术标准》[11]进行综合取值,具体各车站抗浮设防水位取值分别如表3～表5所列。

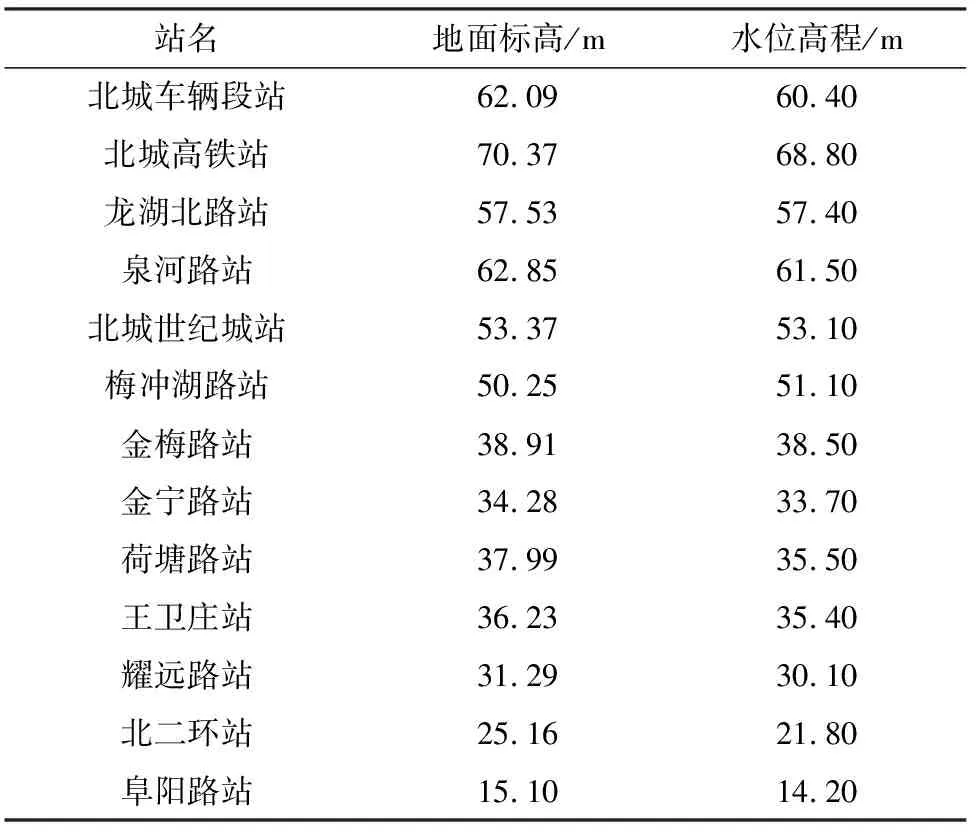
表3 8号线1期抗浮设防水位

4 结论

(1) 以合肥市轨道交通工程地下车站为研究对象,根据合肥市的水文地质条件,结合大气降水、蒸发、河流条件和合肥市近年的地下水监测资料,构建地下水三维渗流数值模型。模型经识别验证后,预测百年一遇降水量情况下研究区各地下车站的最高地下水位。预测结果显示,地下水埋深呈现西北高、东南低的特点,与研究区地形趋势一致,研究区北部非硬化区车站站点水位相比历史最高水位抬升1.2～3 m,研究区中部硬化区车站站点水位相比历史最高水位抬升0～0.7 m,研究区南部车站站点水位相比历史最高水位抬升1～5 m。预测各车站的最高地下水位经修正后可作为各车站的抗浮设防水位,结合地下水数值模拟与频率分析法确定的抗浮设防水位与场地最高水位相比,其结果更加科学、安全。

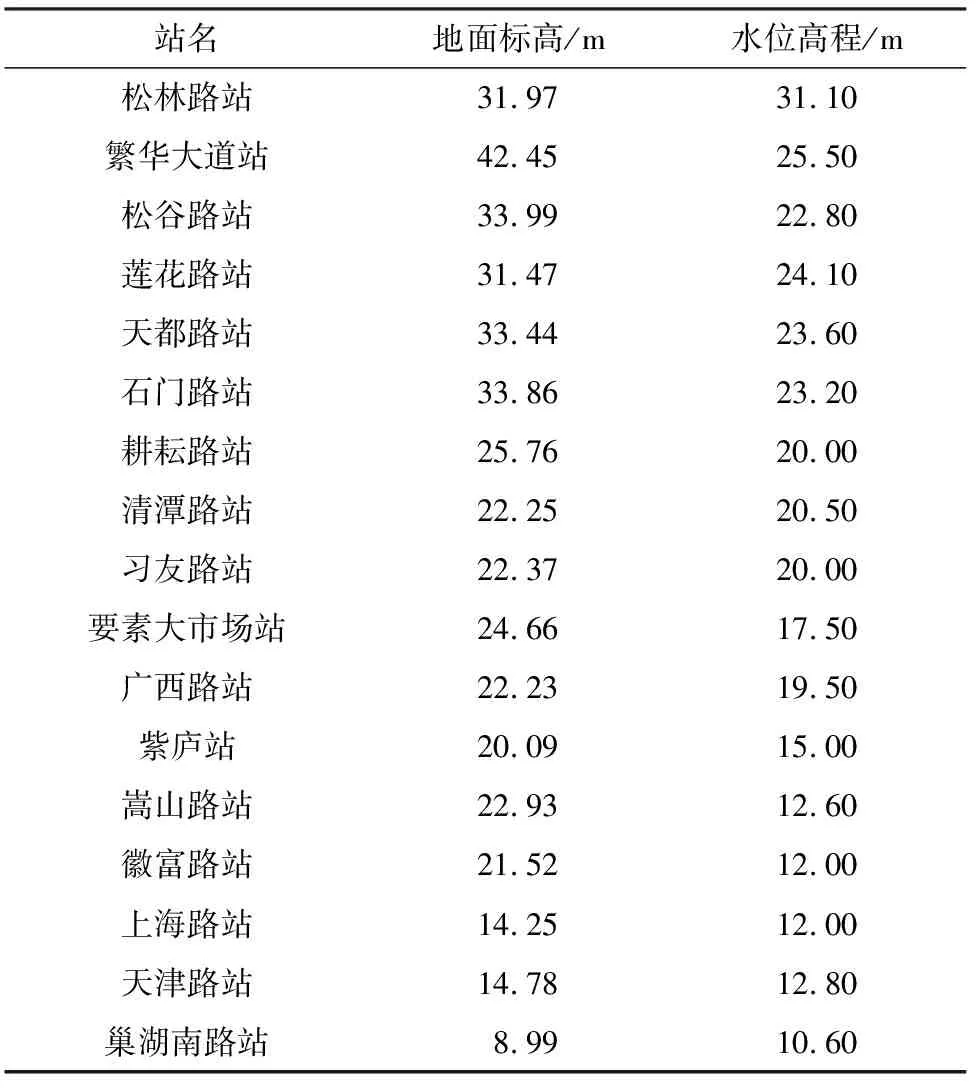
表4 7号线抗浮设防水位

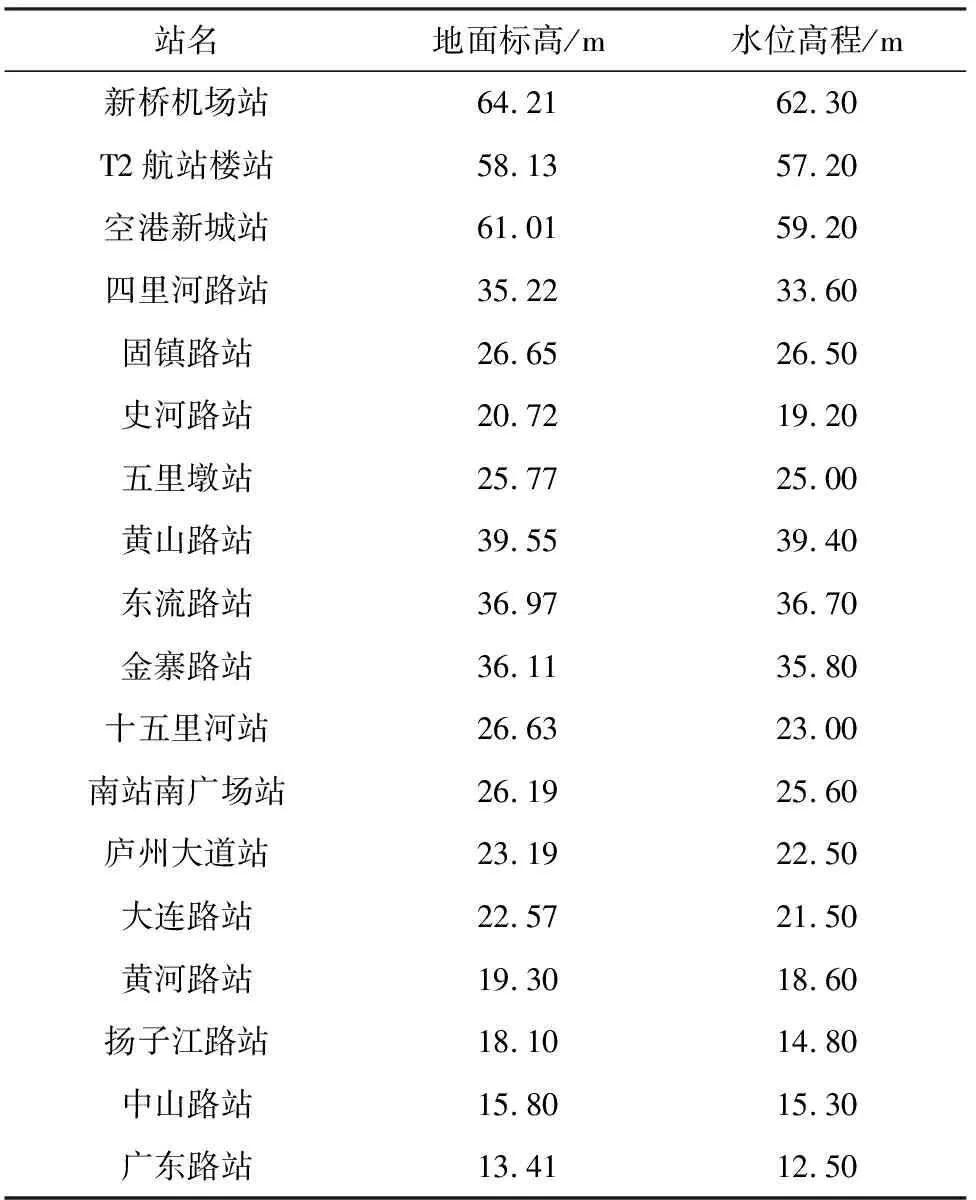
表5 S1号线抗浮设防水位

(2) 建立以地下水分水岭与河流为边界条件的区域数值模型,避免了人工边界可能对预测结果产生的负面影响,以钻孔与地表DEM数据联合建立的三维模型充分还原了合肥市地层结构,并通过人工与PEST程序调参,得到了高可信度的区域数值模型,最后预测计算得出科学合理的抗浮设防水位。通过建立水文地质数值模型加深了对区域水文地质情况的了解,为合肥市地铁工程车站抗浮设计提供了技术支撑。

(3) 因施工方案在勘察阶段并未固化,提出的抗浮设防水位仅为建议值,如果施工原因导致场地的水文地质条件发生了变化,其抗浮设防水位也应做出相应的修改。