考虑外部成本下政府规制的供应链决策

李雨霖,周 刚

(天津大学管理与经济学部,天津 300072)

随着我国经济不断发展,各种日常用品的产能不断提升,废品造成的污染若不经过分类处理,对环境的危害会越来越大。另一方面,随着我国环保政策力度逐渐加大,政府对于废品处理的补贴与监管措施建立健全,各个城市垃圾分类迅速推进,废品回收处理体系也日趋完善。废品的处理方式分很多种:部分特殊废品可以得到该产品制造商的回收,经过少量加工即可再次进入该供应链;部分商品会被第三方回收商回收,经过加工成为再生料,可以用于其他商品;而部分废品只能通过燃烧等方式回收废热或者填埋。在部分供应链中,因为废品的污染较高且回收价值较低,如废弃电器电子产品、废塑料、废旧橡胶制品等,所以这些废品的处理需要政府奖惩作为外部刺激,否则供应链中各成员会缺乏回收的动力。因此,对于供应链中政府作用和外部成本的研究也越来越受到学者的重视。

大量文献探讨过政府对于供应链成员不同的奖惩机制,如Sheu等[1]使用三阶段博弈论模型分析了政府财政干预对绿色供应链竞争的影响,得出了政府和连锁成员决策的纳什均衡解;徐兵等[2]构建了多个模型,给出了政府实现经济环境综合效益最大化的补贴策略,研究发现政府回收再制造补贴能使企业提高回收价,提升废旧品的回收量和回收率;Ma等[3]分别分析了政府资助计划绩效之前和之后渠道成员的决策,发现所有购买新产品的消费者、制造商和零售商在不同程度上都是政府消费补贴的受益者;Zhang等[4]研究了2种价格竞争模型,在信息不完全的情况下采用两阶段Stackelberg博弈,发现政府不能对企业过度收税或补贴,环境对集中式供应链的影响要大于分散式供应链;Wang等[5]发现两周期闭环供应链中的奖惩措施对制造商的影响大于单周期闭环供应链中的制造商,在奖惩强度较高的情况下尤为明显;李新然等[6]探讨了政府再造品置换补贴和废旧品回收奖惩双重干预对闭环供应链最优决策的影响,以社会福利最大化为目标分析了政府的最优干预参数;范定祥等[7]研究了回收商和消费者组成的两级回收供应链演化博弈模型,分析了双方的演化均衡点及参数变化对回收积极性与策略的影响,以及不同的参数区间下政府单边惩罚补贴机制对回收供应链积极性提升的作用。在有关信息不对称下的补贴方面,王文宾等[8]根据委托代理理论,研究了没有奖惩机制与政府对回收商实施奖惩机制的2个模型;王新辉等[9]研究了分散决策下的具有双边不对称成本信息的供应链协调问题,给出了一个基于双方期望信息租金的分配规则,并设计了一组改进的转移支付及其协调机制;李芳等[10]研究了政府规制下非对称信息对闭环供应链差别定价的影响,构建了政府、制造商、零售商和消费者的三阶段博弈模型,分析了政府奖惩政策下闭环供应链各成员的最优定价策略,并且将外部成本纳入计算;Ding等[11]为了激励供应链中的企业减少环境外部性,考虑政府的政策激励措施,建立了包含可持续约束的集成供应链定量模型;彭志强等[12]基于政府补贴的不同模式,分别建立差别定价下不同模型,研究了政府补贴下新产品与再制品差别定价的闭环供应链决策及协调机制问题,研究结果表明制造商在政府补贴下会相应提高再制品的批发价格;苑希港等[13]研究了一个两级绿色供应链系统,其中绿色产品的市场需求由产品价格和产品绿色度共同决定,得到了3种情形下的批发价、产品绿色度、零售价、生产商和零售商利润的最优解。

综上,学者从各个方面研究了政府的不同补贴措施对于不同类型的供应链定价决策的影响,研究内容涉及供应链各方的合作、演化博弈、公平关切问题、信息不对称问题、产品的绿色度、闭环供应链等。但目前的文献大多数着眼于供应链中各个成员的收益,讨论政府决策,将供应链外部成本纳入计算的研究相对较少,而且大多与闭环供应链有关。之前多数文献提到的回收商起的只是收集废品、获取残值的作用,并没有对废品进行无害化处理。此次研究加入了对于政府补贴决策的分析和对包含外部损益的社会福利的计算。

1 模型设定与相关假设

假设供应链由一个制造商、一个销售商、一个回收处理厂组成,为简化模型,回收处理厂既负责回收也负责无害化处理。该产品在使用过后,其废品已经不适合用于制造相同或相似的新产品,只能用于回收残值,该产品的残值较少,但若不进行正规处理则会严重污染环境,产生较大的外部成本。政府根据回收量对处理厂进行补贴,根据制造商的产量来征税。这是一个四阶段博弈的供应链,模型如图1所示(模型中各字母的含义在假设中进行解释)。

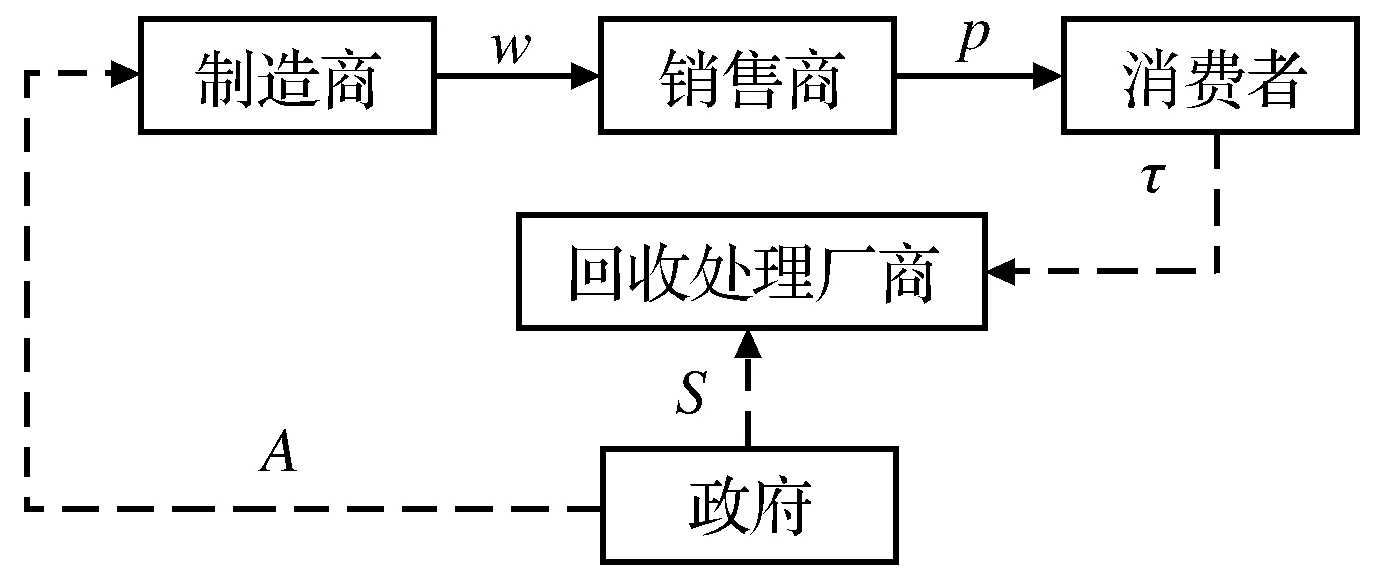
图1 模型1:政府直接补贴回收处理厂商的模式Fig.1 Model 1:The model of the government directly subsidizing recycling companies

假设1该供应链中,政府综合考量社会福利,供应链中其他成员都以利润最大化为目标。为简化计算,模型中只含一个制造商、一个零售商、一个回收处理厂商。

假设2由于该产品的生产过程以及最终产生的废弃物会对环境造成污染,在该闭环供应链中,政府对制造商生产的每单位新产品征收费用为A,要求p-cm-cr-A>0(其中:cm为制造成本;cr为销售成本),否则制造商不会生产该产品。

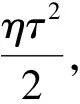
假设4每单位产品在生产过程中对环境产生的外部成本为E1,E1包括不可再生资源的消耗,以及可能出现的废气废水与固体废弃物的排放;每单位未经处理的废品对环境的外部成本为E2,即未经处理的废品对环境污染的影响;垃圾处理过程中产生的外部成本为E3,该过程也有可能消耗掉一些不可再生资源,产生废气等。设E2-E3-O>0,政府才有动机促成废品的无害化处理,否则回收没有必要。E1、E2、E3均受到政府部门的实时监测,该信息对于供应链各个成员都是透明的。

假设5为了便于计算,假设消费市场对于商品的需求是确定性线性需求,市场的需求函数为q=α-βp,其中:p为市场价格;q为市场需求;α为产品的市场容量;β为产品的需求价格弹性。假设α-β(cm+cr+E1+E2)>0,以保障供应链的效益。

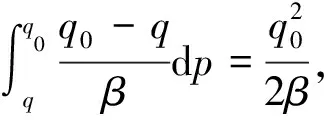
研究中出现的各个符号的含义见表1。

表1 相关符号和表述

2 博弈分析

2.1 政府直接补贴回收处理厂商的定价策略

模型1下,总社会福利为

制造商、销售商、回收处理厂商的收益分别为

πm=q(w-cm-A),

πr=q(p-cr-w),

用逆向归纳法进行计算:

第四阶段:确定第三方回收的回收率τ,用πt对τ求一阶和二阶偏导数,可得

令

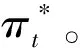
第三阶段:确定销售商的售价p,用πr对p求一阶和二阶偏导数,可得

令

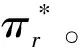
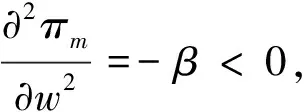
第一阶段:确定政府的单位征税和补贴额度,用πg对A和S分别求一阶偏导数和二阶偏导数矩阵,求出政府对制造商征税和对回收处理商补贴的最优值A*和S*,即

将S*代入πg对A和S的二阶偏导数矩阵中,即

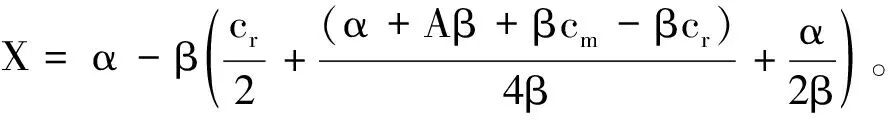
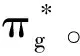
命题1政府对制造商收取的最优环保税额A*是产品在生产过程中对环境产生的单位外部成本E1的增函数。政府对回收商最优补贴额度S*是未处理废品造成的单位外部成本E2和回收商无害化处理废品的净成本O的增函数,是E3的减函数。

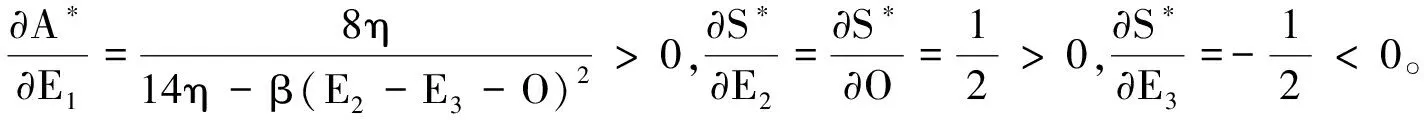
因此,当产品在生产过程中对环境产生的外部成本增加时,政府会增加对制造商征收的每单位产品环保税。

供应链各成员的决策变量与各方利润以及社会福利分别为

由0≤τ≤1可知,需要满足

(α-β(cm+cr+E1+E2))(E2-E3-O)<

14η-β(-E2+E3+O)2

模型中供应链各成员利润的计算才有意义。若

(α-β(cm+cr+E1+E2))(E2-E3-O)≥

14η-β(-E2+E3+O)2,

则τ=1,理论上可以实现废品的完全回收,但本文不讨论这种情况。

命题2在政府直接补贴回收商的模式中,制造成本和销售成本的增加,都会使得制造商和销售商的利润减小。制造成本和销售成本是制造商利润的凹函数,也是销售商利润的凹函数。

证明

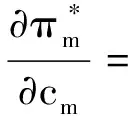
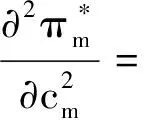
可证明上述命题。所以制造商和销售商都有动机提高管理水平,降低运营成本以及相互帮助对方降低运营成本。同理,cm、cr的减小同样有利于增加回收处理商的利润与社会福利。

命题3回收率、出厂价格、销售价格以及供应链各成员的利润和社会福利都是产品在生产过程中对环境产生的单位外部成本E1的减函数,产量是E1的增函数。其中回收率、出厂价格、销售价格是E1的一次函数,供应链各成员的利润以及社会福利是E1的凹函数。

证明

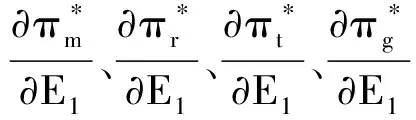
命题4若改进制造技术，通过增加制造成本以减少制造过程的外部成本。设此时的制造成本为c′m，制造过程的外部成本为E′1，设Δcm=c′m-cm>0，ΔE1=E′1-E1<0 。根据求解出的博弈后的利润函数可知，若Δcm+ΔE1<0 ，则制造商会改进自身技术，提高制造成本以降低外部成本。若Δcm+ΔE1>0，则制造商不会改进自身技术，提高制造成本以降低外部成本。

2.2 政府间接补贴回收处理厂商的模式

在进行以上博弈机制下,若要减弱双重边际效应,则应该加强供应链各成员的合作。在模型1求出的政府对制造商征税的基础之上,减少政府征收的环保税的额度,取消政府对回收处理厂商的补贴,改由制造商对回收处理厂商补贴。实际上政府间接补贴了回收商。假设把A*代回政府征收的环保税的额度,改由制造商对回收处理厂商补贴,每单位废品的回收进行补贴的额度为F,政府相应减少对制造商的征税额度,对于每单位废品的回收,对制造商征收的环保税减少B,即制造商与回收商可以与政府三方对接,在政府监督下,制造商承担对于回收商的补贴,换取政府对其环保税征收的减少,模型如图2所示。

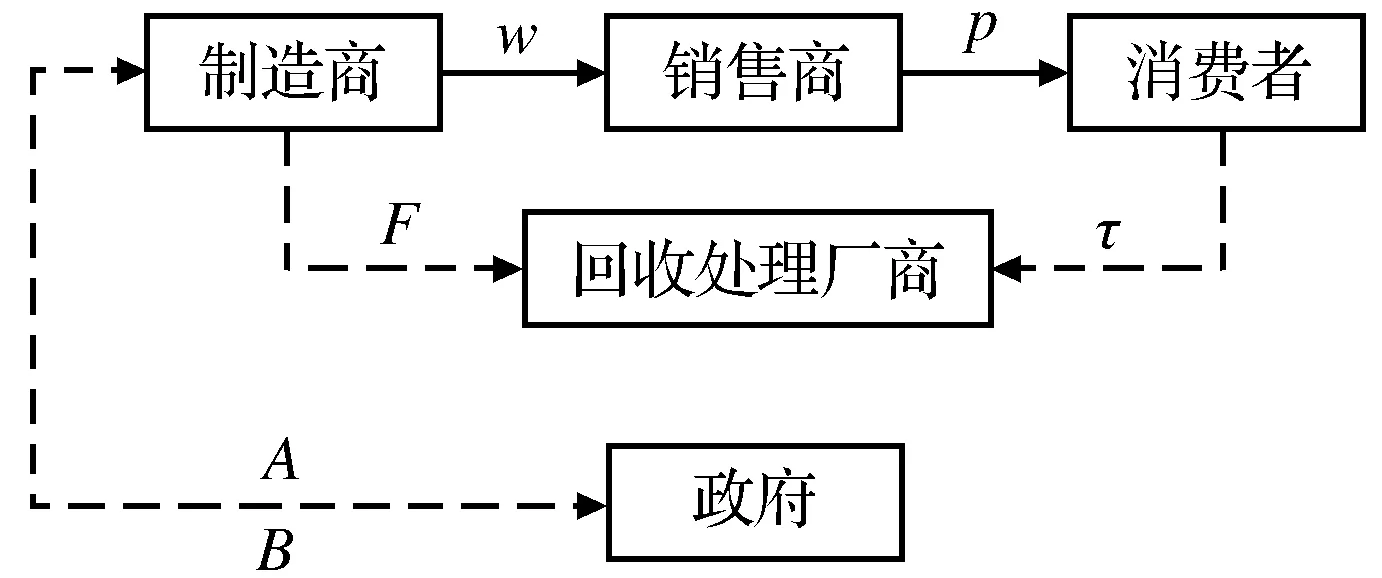
图2 模型2:政府间接补贴回收处理厂商的模式Fig.2 Model 2:Government indirectly subsidizing recycling companies

此时总社会福利为

制造商、销售商、回收处理厂商的收益分别为

πm=q(w-cm-A*)+τq(B-F),

πr=q(p-cr-w),

同样使用逆向归纳法,通过三阶段博弈,求出制造商的最优出厂价格与对回收商最优补贴额度,即

将FC代入πm对w和F的二阶偏导数矩阵中,可以得到

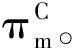
其中:

Z1=-αη+β(-7A+cm+cr+8E1+8E2)η+αβ(B-E2+E3)(B-O)-β2(B-O)·

(-cmE2-crE2+B(cm+cr+E1+E2)+cmE3+crE3-E1O-E2O+A(-E2+E3+

O)),

Z2=α(-28η+β(B-O)(5B-4E2+4E3-O)),

Z3=-4(7(cm+cr)+8(E1+E2))η,

Z4=β(B-O)(-4crE2+B(5(cm+cr)+

4(E1+E2))),

Z5=β(B-O)(4crE3-crO-4E1O-4E2O-

c1(4E2-4E3+O)),

Z6=A*(4η+β(B-O)(B-4E2+4E3+3O))。

对B的求解涉及四次方程求根,故在此不求解析解,在算例分析部分求数值解。

3 算例分析

直接采用数值算例来体现各个因素对于供应链的影响,比较完全信息和供应链其他成员在销售商的销售成本信息不对称情况下,销售商的利润以及供应链总体收益。假设α=100,β=4,E1=3,E2=8,E3=3,O=3,η=40,cm=1,cr=1,各个参数所假设的值应该满足题设和推论过程中给出的所有约束条件。此时满足

-14η+β(-E2+E3+O)2=-224<0,

α-β(cm+cr+E1+E2)=48>0。

3.1 在政府补贴回收商的模型中,讨论外部成本的影响

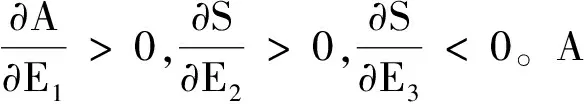
由图3可知,政府对于每单位新产品征收的环保税A与废品处理过程中产生的外部成本E3正相关,A随E2的增大先增大后减小。根据命题4,供应链各个成员的利润以及社会福利都是产品在生产过程中对环境产生的单位外部成本E1的减函数。由图3也可知A是E2和E3的凸函数。

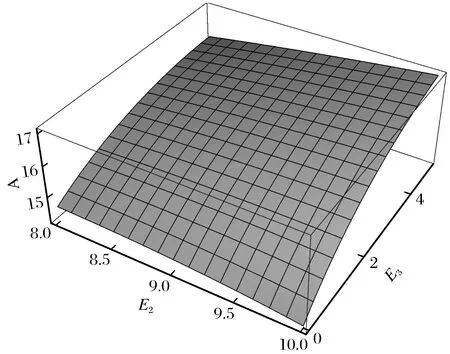
图3 A与E2、E3的关系Fig.3 Relationship between A and E2,E3

(2) 外部成本对回收率的影响 根据命题3,回收率τ是产品在生产过程中对环境产生的单位外部成本E1的减函数,现在把E2和E3作为自变量,作图求解它们对τ的影响,如图4所示。

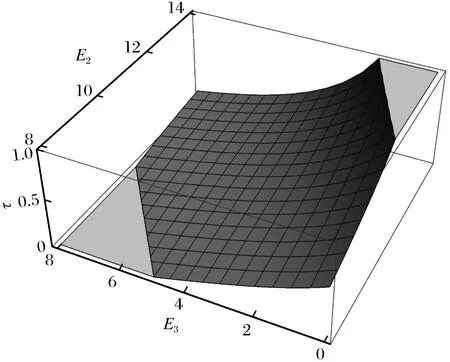
图4 回收率与E2、E3的关系Fig.4 Relationship between recovery rate and E2,E3

由图4可知,回收率τ是E2的增函数,是E3的减函数。未处理的废品对环境污染越大,则回收处理厂商的回收率越高。而处理废品的外部成本越高,越不利于回收率的提高。

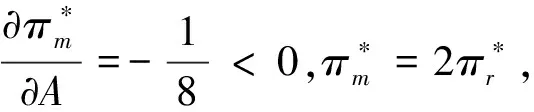
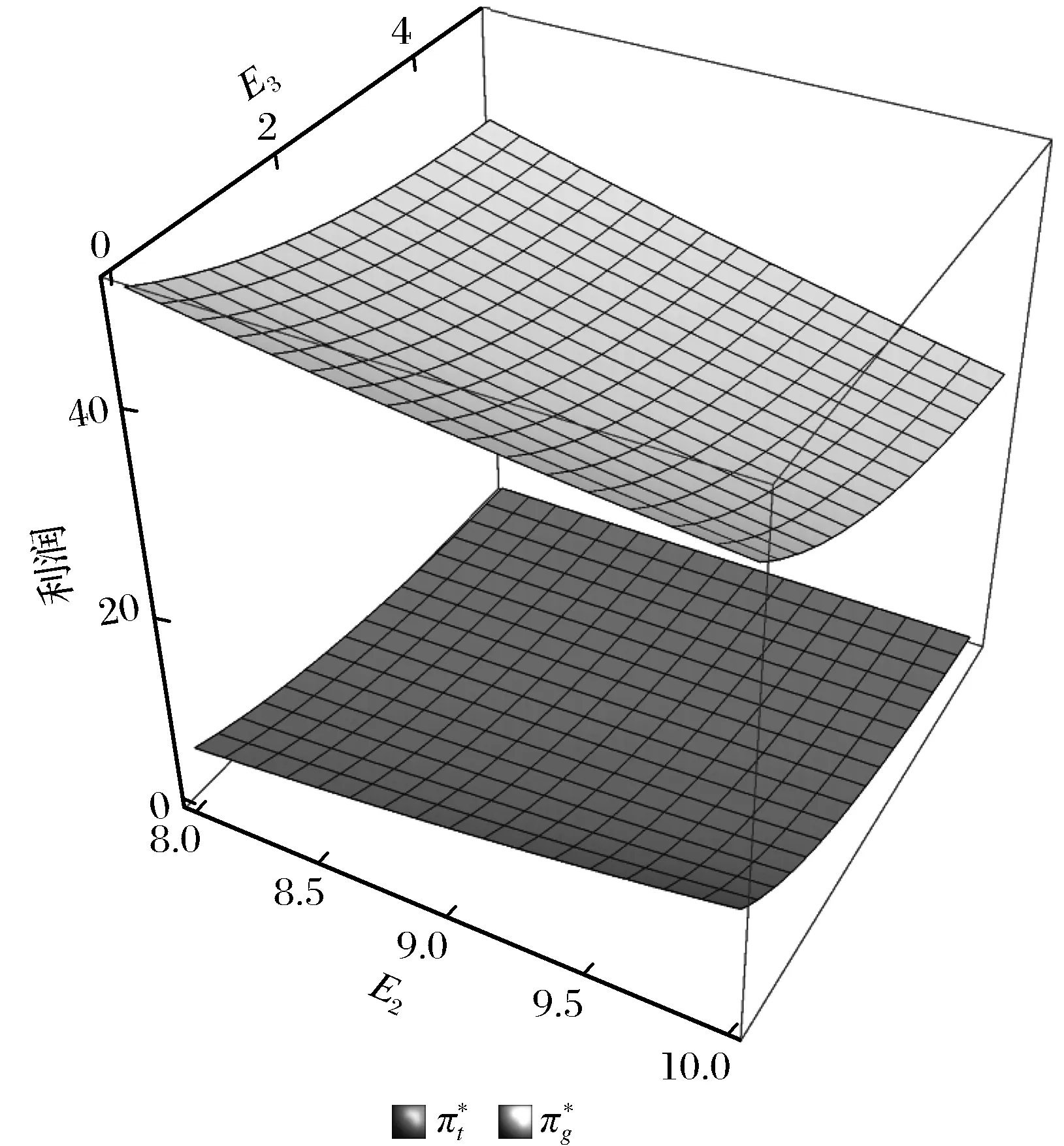
图与E2和E3的关系Fig.5 Relationship between and E2,E3

3.2 两个模型的利润对比

在制造商补贴回收商的模式中,代入研究中设定的各个参数,得到政府对制造商征收的单位产品环保税的不同减免额度下,供应链各成员的利润和社会福利情况,如图6所示。

由表2可知,如果改由政府对回收商间接补贴,即制造商对回收商进行补贴,政府减少对制造商征收的税额,则供应链各成员的利润都会增加,回收率和社会福利也会增加。在政府能够实现对于制造商和回收处理厂商的监管的情况下,供应链各成员都有意愿采用模型2的间接补贴的模式。

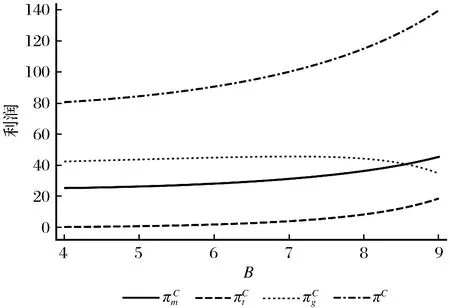
图6 政府对环保税的不同减免额度下各成员利润Fig.6 The profit of each member under the different reduction of the government environmental tax

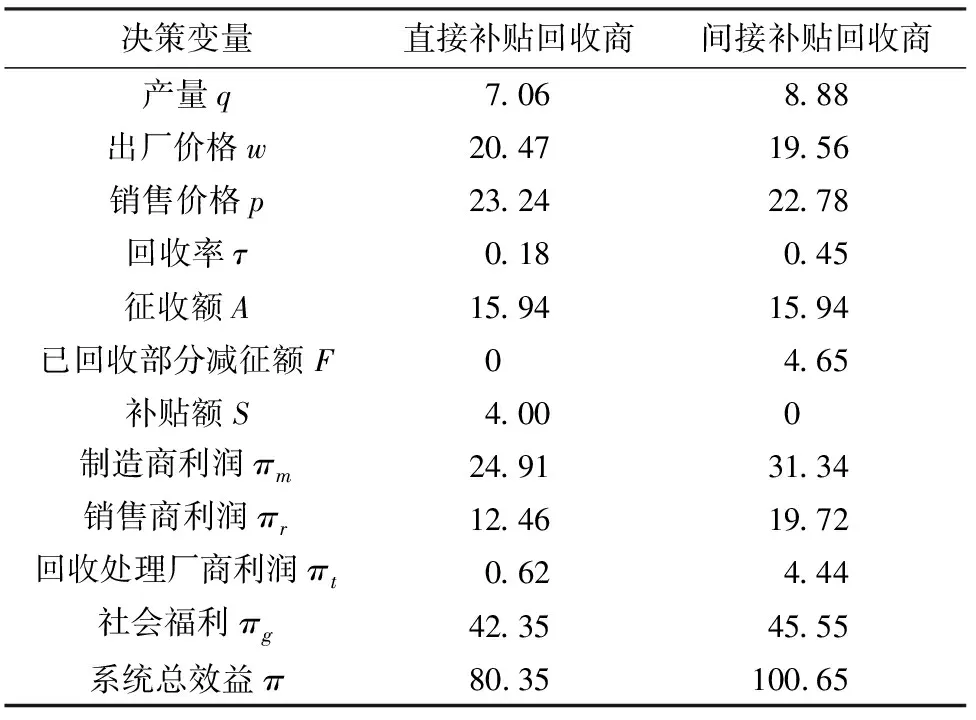
表2 政府直接和间接补贴回收处理厂商时决策与 收益算例分析

4 结论

通过建立一个四阶段供应链模型,计算出了在政府对制造商收税并补贴回收商的情况下,回收商的最优回收率与制造商和销售商的定价策略,并求出了政府最优的税收和补贴策略。再以此为税收标准讨论制造商补贴回收处理厂商的模式,求出了制造商对回收处理厂商最优的补贴额度并且得出了政府减少征收环保税的最优额度的数值解。然后分析在政府补贴回收处理厂商的情况下3种外部成本对于供应链各成员决策和利润的影响。结论如下:

(1) 在政府直接补贴回收商的模式中,产品在生产过程中对环境产生的外部成本与废品处理过程中产生的外部成本的增加会使政府对制造商的单位环保税、商品售价增加,回收率、供应链各成员的利润和社会福利降低;未处理废品造成的外部成本的增加使得制造商和销售商的利润先减后增、回收率和回收商的利润增加,社会福利减少。

(2) 政府间接补贴回收处理厂商的模式中,供应链各成员的利润和社会福利都高于政府直接补贴的模式,所以供应链各成员均有动力采取这个模式,该模式可以进一步探索。也可知供应链各成员应该加强相互协作,才能减弱双重边际效应,提高各个成员的利润和社会福利。

研究假设的是单一制造商、单一销售商、单一回收商的情况,而且市场需求固定,供应链各方信息对称,这属于一种理想的情况。实际情况下制造商、销售商、回收商都可能有多个,市场需求可能有波动,供应链成员也有可能对其他成员隐瞒信息,这些都能成为未来的研究方向。