基于人工神经网络的技术生命周期测度方法研究
柴鑫慧
(大连理工大学人文与社会科学学部,辽宁 大连 116024)
0 引 言
技术生命周期是反映技术发展的历史、现状与未来趋势的重要指标,是企业技术战略制定的基础,行业发展潜力的参考,政府制定政策的依据。如何有效地判断技术生命周期无论是从微观还是宏观上来说都有着重要的意义。关于生命周期的研究起源于对自然生态系统中的事物从产生到消亡的发展趋势的研究,继而发现在社会系统中事物的生命周期与自然生态系统有着相似性,而后其成果和理论逐渐得到了推广应用。技术生命周期的概念起源于1966年哈佛教授Raymond提出的产品生命周期理论[1],1978年Abernathy和Utterback首次明确提出了技术生命周期的概念:认为技术的发展过程可根据其表现出来的特征划分为导入期、成长期、成熟期与衰退期4个阶段[2]。1981年Arthur D Little公司根据技术与产品的结合程度对“四阶段”技术生命周期的含义进行了更进一步的解释[3]。Harvey等(1984)和Khalil T M(2000)将技术生命周期分为开发阶段、验证阶段、技术开始应用阶段、扩张阶段、成熟阶段、衰退阶段6个阶段[4-5]。无论划分为几个阶段,学者们对由这些阶段连接起来的技术发展全过程所表现出来的特征有着基本的共识。
1 方法回顾
识别技术生命周期阶段的方法多种多样,目前还没有一个权威的方法,不同的方法在特定的情景下具有各自独特的优势和局限。常用的定性类方法有德尔菲法、TRL技术成熟度法等等,这类方法往往依赖于专家的经验,主观性较强。常用的定量分析法包括S曲线法、科学计量法、专利分析法等等,这类方法得到的结果往往受到数据量、参数和模型的限制。无论是定性方法还是定量方法,基于专利数据库实现的模型应用较为广泛。这是因为专利本身包含了许多以前的秘密技术知识,揭示了关于该技术发展的信息;同时专利可以揭示技术的商业潜力,因为专利申请的目的是保护可能的商业应用[6]。
Forster阐述的技术生命周期发展趋势特征符合S曲线的一般形式。以专利申请数量的演变来反映技术对投资的吸引力而形成的S曲线较广泛地被用于技术生命周期的预测(例如Andersen,1999;Tseng等,2011;张丰等,2017)[7-9]。其中,Logistic回归分析方法在S曲线的拟合上运用较为成熟。葛亮(2015),周曼等(2017),Jamali等(2016)都采用Logistic模型对TLC进行分析[10-12]。然而在Logistic模型中假设曲线在拐点处中心对称,这有可能与专利数量演变的实际情况出入较大。Fisher-pry模型广泛应用于对技术成熟度的分析,是目前较为准确的方法之一[13];李欣等(2013)和靳军宝等(2018)都采用这种方法来研究技术发展趋势[14-15]。TRIZ(Theory of Inventive Problems Solving)理论的技术生命周期判断方法也比较成熟,王秀红等(2008)和高常青等(2014)等采用这种方法进行了技术预测[16-17];但这种方法对专利级别与性能数据的要求较高,操作难度较大大。
近年来随着数据挖掘技术的发展,一些基于机器学习的方法也不断出现,比如:Segev和Kantola(2012)利用自组织映射方法预测专利趋势[18];郑炳基和高南旭等(2016)利用深度神经网络构建专利寿命的预测模型[19];Saade和Jneid等(2019)使用宽深神经网络和复发神经网络进行技术预测[20];Xin Z和Zhang等(2019)运用面向短时间序列的神经网络算法计算技术生命周期[21]等等。这些方法在一定程度上进行了一些优化,可以对专利数据进行更深度的分析,使得对技术生命周期的探索更为准确。
2 模型构建
人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统,是可用于预测估计的一种智能方法,其在优化预测方面的能力为专利数据库的分析提供了更大的机会。神经网络在拟合非线性数据方面表现出显著的能力[22],即使是具有不完全信息和错误信息的数据集[23],也能获得较好的拟合结果。对于信息不完备的专利数据库来说,利用人工神经网络的学习功能可以对未来专利数量的发展趋势进行预测,从而拟合出技术的生命周期曲线,并据此来判断技术的生命周期。本文运用人工神经网络和专利数据库测算技术生命周期的过程包含4个步骤,每个步骤涉及的具体方法和操作如图1所示。
2.1 专利数据检索
专利数据检索是对作为研究对象的技术相关的专利进行数据的检索,本文选取德温特专利数据库作为数据来源。德温特专利数据库(Derwent Innovations Index)是全球范围内国际型专利信息收入最全面的数据库之一,收录了自1963年以来全球40多个专利机构(涵盖100多个国家)的一千多万条基本发明专利,以及两千多万条专利情报,可以得到较为全面和可靠的专利数据。运用研究对象关键词进行专利检索,选定时间阶段和步长,得到每个时间点(t)的专利累计数量(x),就是本文研究所需的基础数据。
2.2 建立BP神经网络拟合专利数据
以时间点(t)为输入,对应的专利累计数量(x)为输出,建立BP神经网络,来探究输入与输出之间的关系,并对专利增长趋势进行预测。为了提高神经网络的泛化能力,避免过度拟合的现象,要根据数据特征选择合适的处理方法。
本研究构建了一个浅层网络来研究输入和输出之间的关系,选取贝叶斯正则化方法来对网络进行训练。该方法可以减小网络的权重和偏置,迫使网络响应更平滑,降低浅层网络过拟合的可能性。贝叶斯正则化方法训练网络通过Matlab中的trainbr函数实现,而该方法要求输入和输出在[-1,1]的范围内,以取得更好的训练效果,因此在对网络进行训练之前还要对输入数据进行归一化处理。
设定好相关参数和方法后,对建立好的神经网络进行训练,并用训练好的网络对专利数量变化的趋势进行预测,将预测结果反归一化以后绘制出技术的全生命周期曲线,并找出其拐点与饱和点。
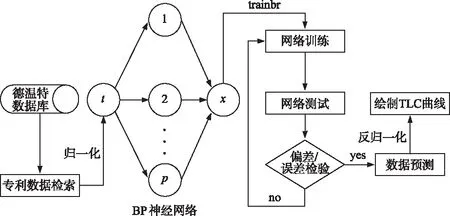
图1 模型结构图
2.3 Logistic回归方法拟合专利数据
以时间点(t)为自变量,专利累计数量(x)为响应变量,对专利数据进行Logistic回归;选择合适的参数估计方法以保证预测结果的合理性,用得到的拟合曲线对专利数量变化趋势进行预测。
Logistic方程定义如下:
(1)
其中,a,b,c为模型的参数;对参数的估计采用Yule迭代法:
(2)
令
(3)
原方程可以变形为:
zt=γ+βxt
(4)
根据数据样本对γ和β进行估计可以得到a,b,c的估计值,从而拟合出Logistic曲线。
2.4 测算结果比较分析
比较BP神经网络拟合专利数据和Logistic回归方法拟合专利数据得到的TLC曲线的形态、拐点、饱和点的差异;同时对上述两种方法进行误差分析,评价两种模型的优度。本文采取的误差指标如表1所示(n表示样本量)。
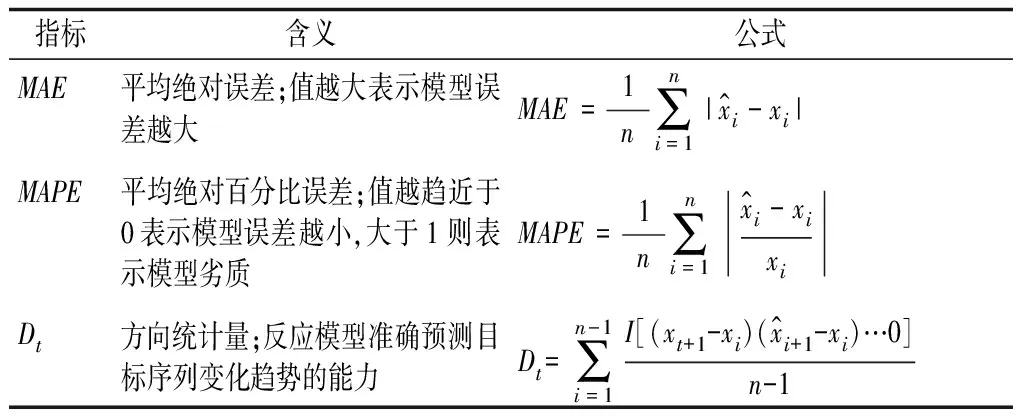
表1 误差指标公式及含义
3 算例分析
3.1 专利数据检索
本文以高温气冷堆(The high-temperature gas-cooled reactor,HTGR)技术为例,对其技术生命周期进行探究。HTGR是一种先进的第四代核电堆型技术,凭借其高效率、安全性、经济性等优势在能源领域得到广泛的应用[24]。尤其是在人们已经了解到重大核事故会对人类造成怎样无法挽回的危害的背景下,如何保证安全性已经成为核能源领域的首要议题。高温气冷堆就是在这种背景下发展起来的新的先进堆型。它是目前国际核能领域中6种第四代核能系统的首选堆型之一。本文基于德温特专利数据库,选取相关的专利数据对HTGR技术的生命周期进行预测。共检索到自1968年至2020年的6 111项专利,选取步长为1年,得到其累计数量如图2所示。
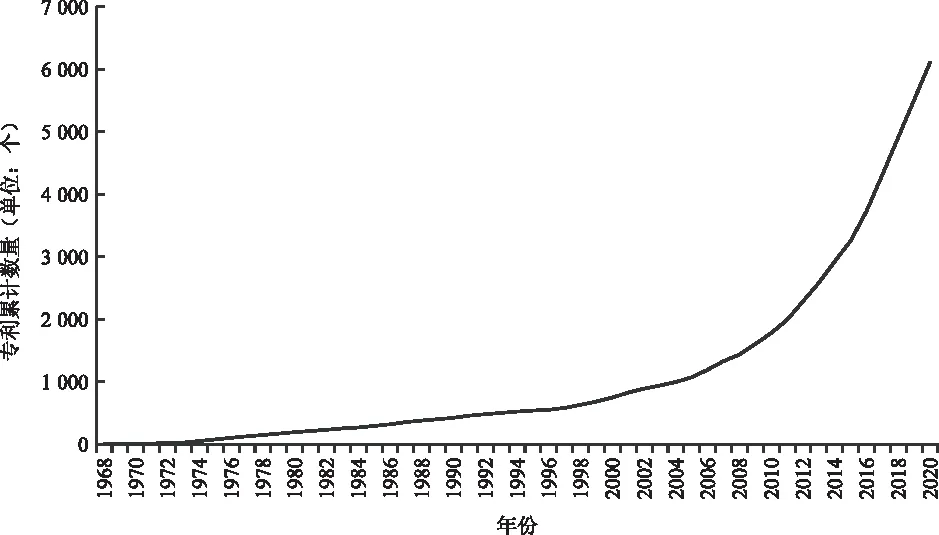
图2 HTGR专利累计数量
3.2 建立BP神经网络拟合专利数据
将专利申请年份作为输入特征,专利累计数量作为输出特征,构建一个包含10个隐含层(隐含层数量根据输入和输出数据规模和经验公式估算而得),激活函数为Sigmoid函数的BP神经网络。采用贝叶斯正则化方法来提高网络的泛化性,采用梯度下降法减小损失函数,来对网络进行训练。
用训练好的神经网络预测自1968年起100年时间内的HTGR专利累计数量,得到的结果如图3中神经网络生长曲线所示。从图3和表2可看出,专利累计数量的饱和值在2036年达到8 174,90%成熟点在2023年达到,拐点在2020年。
3.3 Logistic回归方法拟合专利数据
将专利申请年份作为自变量,专利累计数量和专利发明人累计数量分别作为因变量进行Logistic回归,参数估计采用yule的迭代算法,拟合出专利累计数量的生长曲线如图3中Logistic生长曲线所示。如图3和表2所示,专利累计数量饱和值在2066年达到8 588,90%成熟点在2027年达到,拐点在2013年。
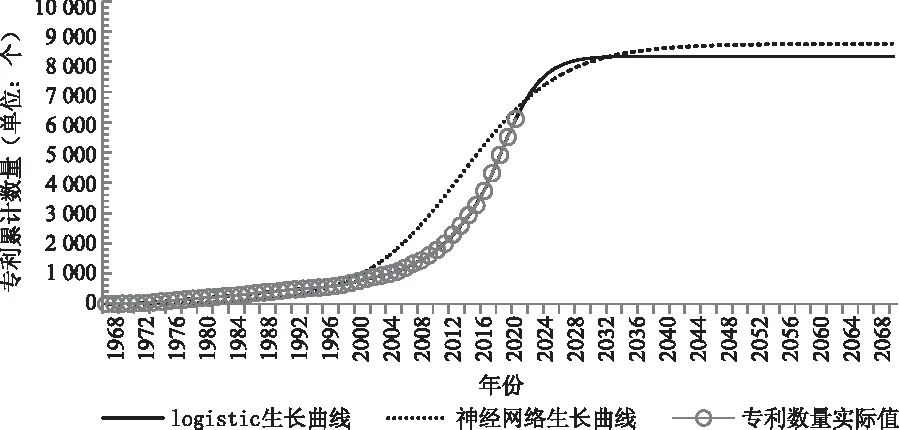
图3 专利累计数量增长趋势图
3.4 测算结果比较分析
从算例的结果来看,运用BP神经网络和Logistic回归方法都拟合出了HTRG技术增长的“S型”曲线,见图3,可以看出BP神经网络方法的拟合效果更优。运用BP神经网络进行拟合的MAE和MAPE值(见表2)都远小于运用Logistic回归方法得到的值,其预测值偏离实际值的程度更小。同时,在预测功能上来看,BP神经网络方法的Dt值更大,其预测效果也优于Logistic回归方法。
从曲线的变化趋势来看,BP神经网络方法得到的S曲线并不是严格关于拐点对称的。从两种方法得到的S曲线的变化程度来看,两种方法得到的拟合曲线所评估的HTRG技术成熟度达到10%和90%的时间节点较为接近,即技术从成熟期走向衰退期的分界点差异很小。

表2 HTRG技术增长曲线拟合效果比较
4 结论与展望
本研究以HTGR专利累计数量为基础,分别使用BP神经网络和Logistic回归方法对其技术生命周期曲线进行拟合,研究这两种方法在技术生命周期预测中的不同性能。得到的结论如下:
首先,运用BP神经网络方法测度技术生命周期是可行的。根据算例结果,与传统的Logistic回归方法相比,两种方法对技术成熟时间的估计大致相同,但因曲线形态不同导致在技术成熟期专利累计数量饱和值上有差异。这是因为Logistic函数的性质导致曲线在逼近极大值的过程中变化率变慢。
其次,BP神经网络方法对技术增长曲线的拟合效果和预测效果均优于Logistic回归方法,得到的专利生长曲线更为贴近实际情况。Logistic回归方法是基于TLC曲线关于拐点中心对称的假设,该假设过于理想,可能与实际情况存在一定的偏离;对于发展已经成熟的技术来说,运用该方法判断生命周期误差不大。但在数据规模的限制下,有可能在进行预测时出现对专利增长速度的低估。BP神经网络方法可以修正这种缺陷,得到更为贴近实际情况的非对称S型增长曲线。
再次,BP神经网络方法应用范围更广,不受数据规模的限制。Logistic回归方法操作简便,但在数据量较少时,出现的偏差较大。在数据量充足的情况下,如果仅仅是为了确定技术的生命阶段,logistic回归方法更为便捷。如果研究目的是技术预测,或是数据规模不足的情况下,使用BP神经网络可以得到更好的效果。
本研究提供了一种鉴定技术生命周期的新的思路,可应用于多种技术和领域生命周期的判断或技术预测。但本研究还存在改进的空间,本文采用的单变量专利数据作为输入指标可能会存在可靠性不足的问题,因此在后续的研究中可以继续引入更多的技术衡量指标作为变量,构建多变量输入的神经网络模型来对技术生命周期进行研究。

