基于自适应FFRLS和改进CEKF锂电池SOC的估算

马青云，王顺利，余 鹏，邹传云

(西南科技大学信息工程学院，四川绵阳 621010)

为保护环境和节约不可再生能源，国家大力发展新能源。在新能源中，锂离子电池发展迅速，应用广泛，特别是在新能源汽车[1-2]、大规模储能、特种机器人中起着极为重要的作用。为保护电池和延长电池的使用寿命，提出了电池管理这一理念，包括SOC[3]、SOH、SOP、SOE 等。其中，电池的荷电状态是电池管理最重要的因素之一，影响SOC的因素包括温度[4-5]、电池的老化程度、电池使用环境的噪声等。

常见的估算方法包括安时积分法、开路电压法、卡尔曼滤波法、神经网络法[6-7]、支持向量机[8-9]等。安时积分法虽然简单方便，但SOC的初始状态不易于获得。开路电压法则需要电池搁置一段时间来稳定内部的化学反应，才能保证开路电压稳定。因此，开路电压法只能离线估算。扩展卡尔曼(EKF)和无迹卡尔曼算法(UKF)估算SOC，则是利用一定的方法把非线性系统转化为线性系统。本文提出了用自适应FFRLS 对模型参数进行在线辨识，增加了可实用性。且用遗传算法优化的BP 神经网络预测k时刻EKF 的非线性误差等，不仅可以补偿EKF 的非线性等误差，而且也降低了对等效模型精度的要求。

1 等效建模

1.1 等效模型的建立

在选取电池的等效模型时，可以选取含有RC 电路的模型，RC 电路可以用来模拟电池的极化反应，但RC 电路不宜过多，过多会导致计算越来越复杂。本文构建的是二阶RC等效模型，在普通的Thevenin 等效模型基础上再添加了一组RC 电路，可以更加准确地模拟电池内部的化学反应，RC 阶数也不高，在提高了估算精度的同时，计算程度也并不复杂，二阶RC 等效模型如图1 所示。

图1 二阶RC 等效模型

在图1 中，Uoc表示开路电压，UL表示端电压，R0为欧姆内阻，C1、C2表示极化电容，R1、R2表示极化电阻。根据基尔霍夫斯基定律，分析所构建的戴维南等效电路模型，可得到等效电路的电压和电流表达式，如式(1)所示：

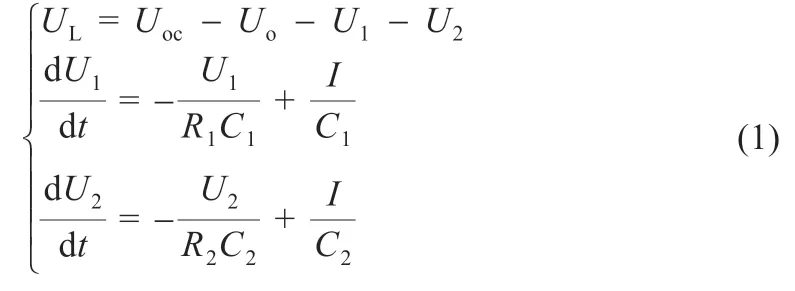
对如图1 所示的二阶RC 等效模型，开路电压可以通过SOC来表示。将等效电路模型离散化，结合SOC定义式(2)，选择状态空间变量、输入变量和输出变量，可以获得离散状态空间方程，见式(3)和(4)：

式中：η 为库仑效率；Δt为采样时间间隔；w为状态误差；v为测量误差；QN为额定容量。

1.2 基于自适应的FFRLS 在线参数辨识

在RLS 的基础上引进了遗忘因子，可以避免数据饱和，弱化旧数据加强新数据的影响。遗忘因子过大，弱化旧数据的能力就很小，遗忘因子过小，跟踪能力虽然增强但抑制噪声的能力就会大大降低，因此提出自适应遗忘因子的FFRLS，递推公式为：

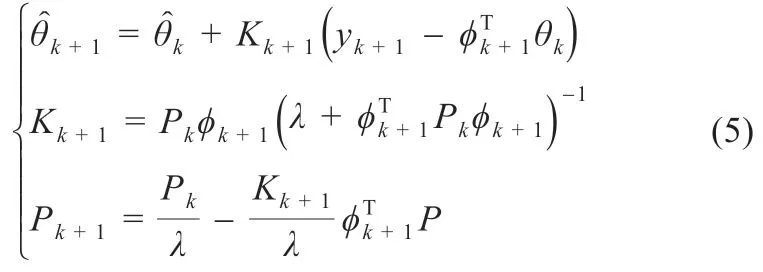
式中：K为递推增益；P为协方差；λ 为遗忘因子；T 为矩阵的转置。遗忘因子的自适应：

式中：εk为预测值与真实值的误差；l为开窗大小；λL为最小遗忘因子；ρ 为阈值。当dk大于阈值ρ 时，遗忘因子立刻减小到λL，随着数据的增加在慢慢增大遗忘因子，以此来增加抗噪能力。

2 CEKF 算法

EKF 通过一阶泰勒展开，虽然使非线性系统转化为线性系统，但是忽略了高阶项，会产生一定的误差。特别对高度非线性电池而言，产生的误差更大，单独使用自适应扩展卡尔曼估算SOC的误差较大。针对此类非线性误差，提出了CEKF 算法，用一些方法去补偿EKF 线性化过程中产生的非线性误差。

2.1 EKF 算法

EKF 算法是估算SOC常用的基本方法。EKF 估算SOC步骤如下：

第一步：计算k时刻的预测值和对应的协方差矩阵。

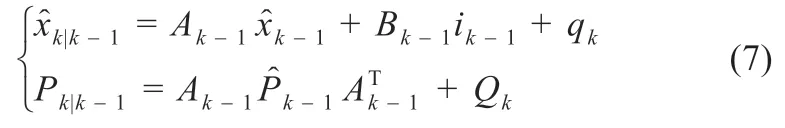
式中：A为状态转移矩阵；B为控制矩阵；P为误差协方差；Qk为外部噪声。

第二步：计算卡尔曼增益。

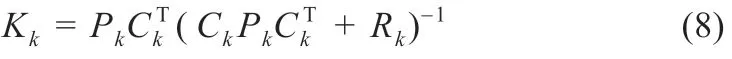
式中：K为卡尔曼增益；C为系统测量矩阵；Rk为测量噪声。

第三步：跟新状态预测值和对应的协方差。

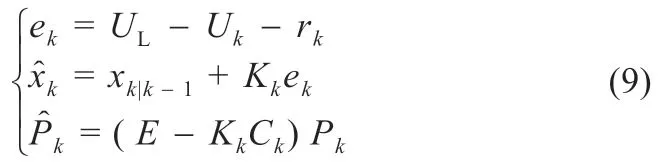
式中：UL为实时所测得的开路电压值；Uk为根据预测值和KVL 定理所得的预测开路电压值。

2.2 改进的GA 优化BP 神经网络

虽然BP 神经网络应用广泛，但是由于无法准确获得最优初始参数和阈值，使得网络训练迭代次数多，训练时间久，每次训练的结果也不一样，且误差也较大等等。因此，针对这些问题，提出用遗传算法优化BP 神经网络，寻找BP 神经网络最优的初始权值和阈值。

普通的BP 神经网络算法采用的是梯度下降法进行迭代训练，但梯度下降法仅利用了目标函数的一阶倒数进行训练。迭代次数较多，迭代时间较长，最终的误差也不理想。因此在梯度下降法的基础上提出了用数值优化的方法去训练，这不仅利用了目标函数的一阶倒数也利用了目标函数的二阶倒数信息。具体描述如式(10)所示：

式中：X k为网络所有权值和偏置值所组成的向量；S(X k)为X的各分量组成的向量空间中的搜索方向；ηk为在S(X k)的方向上，使f(X k+1)达到极小步长。网络权值的寻优就可以分为两个步骤：先确定当前迭代的最佳搜索方向S(X k)，然后在此方向上寻求最优迭代步长。搜索方向如式(11)所示。

式中：H k为海森矩阵，是一个二阶倒数矩阵。开始时，λ 取一个很大的值，此时相当于步长很小的梯度下降法；随着最优点的接近，λ 减小到零。通常f(X k+1)＜f(X k)时，减小λ；否则增大λ。

遗传算法优化BP 神经网络包括：BP 神经网络结构的确定、遗传算法优化权值和阈值、BP 神经网络训练及预测。其中，BP 神经网络一般采用一层隐含层，遗传算法优化BP 神经网络整体流程图如图2 所示。

图2 GA 优化BP流程图

BP 网络部分是四输入和一输出，输入层神经元数为4，隐含层神经元数可选10，输出层神经元数为1，则网络结构是4-10-1。整个BP 神经网络待优化的参数为61 个,编码的二进制位数可以根据自身参数的变化范围和期望精度进行调整，本文权值和阈值编码选择6 位二进制数。为了使预测值和期望值更加接近，选择预测样本的预测值与期望值的误差矩阵的范数作为目标函数输出，即可由目标函数计算适应度函数。选择算子采用随机遍历抽样，交叉算子选择单点交叉算子。

2.3 改进的CEKF 算法

在MATLAB 上建立一个四输入一输出的三层BP 神经网络，隐含层选取神经元10 个，期望值设置为10-5，最大迭代次数为2 000 次，采用L-M 方法训练。遗传算法优化的BP 网络的输入向量是扩展卡尔曼k时刻初始电池SOC的估计值Sk|k-1和极化电压Uk|k-1，SOC的卡尔曼增益KSOC和极化电容的增益KC，输出向量则是扩展卡尔曼估算的SOC和理论值SOC的差值。此算法的本质是，用遗传算法优化的BP 神经网络对EKF 估算的SOC进行非线性等误差补偿，以此来提高SOC的精度。改进的CEKF 整体流程图如图3 所示。

在图3 的SOC估算的过程中，SOC非线性误差补偿的公式为：SOCr=SOCEKF+ErrBP，对EKF 进行非线性误差补偿可以进一步提高SOC的精度，降低了对模型精度的要求。

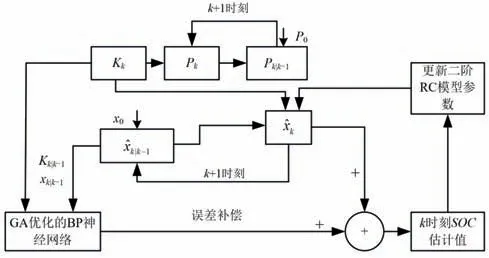
图3 改进的CEKF整体流程图

3 实验验证和结果分析

本实验选取的是出厂容量标定为70 Ah 的三元锂电池，实际测量容量是69.27 Ah，数据读取时间间隔是0.1 s，电压上限为4.5 V，电压下限为2.5 V，电流上限为100 A，电流下限为-100 A，电池相关数据是通过深圳市亚科源科技有限公司提供的BTS200-100-104 实验平台获取的。

3.1 验证自适应FFRLS

DST 在线辨识的预测电压和真实电压如图4 所示。

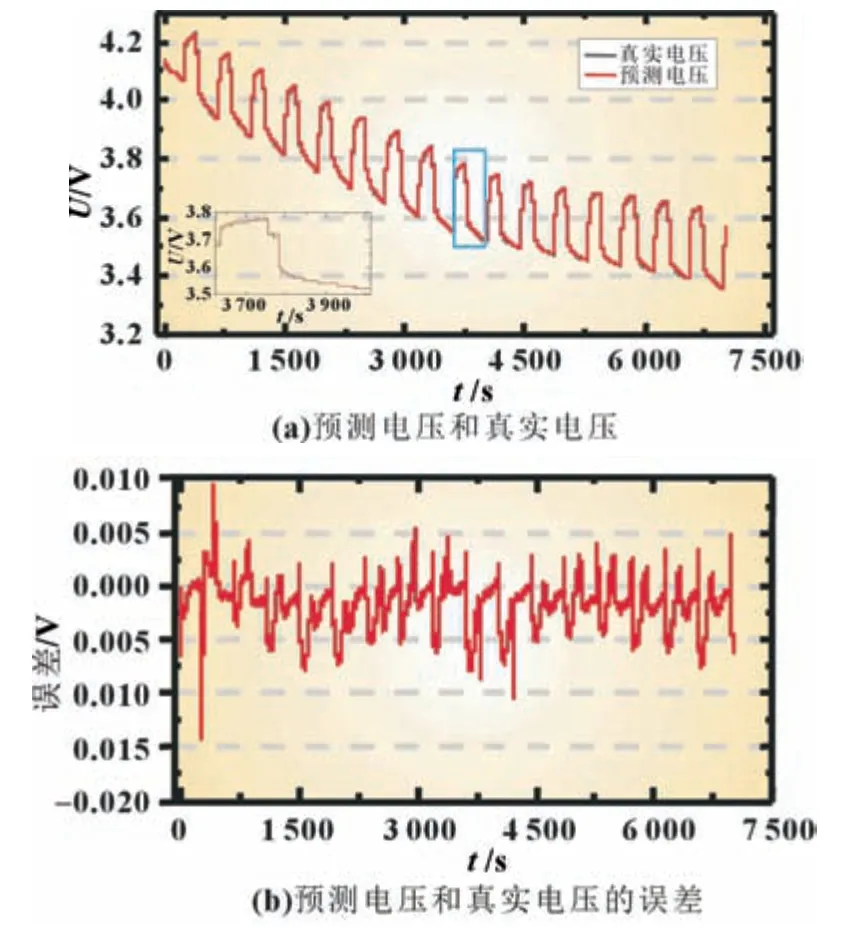
图4 DST电压

由图4 得，预测电压和真实电压的误差最大不超过1.5%，且基本稳定在0.5%内，表明自适应FFRLS 的在线辨识效果较好。

3.2 GA-BP 误差进化曲线

在GA 优化BP 神经网络的过程中，在每代的种群中挑选最优的个体(本文的最优个体是预测值与期望值的误差矩阵范数最小的个体)，记录每代最小误差矩阵范数。误差变化曲线如图5。

由图5 得，种群中的最优个体随着遗传代数的增加而进化，具体表现为随着遗传代数的增加，误差越来越小。把GA优化的最优初值带入BP 神经网络算法，既可以增加神经网络的预测能力，也使BP 神经网络每次运行的结果也一样，增加系统的稳定性。

图5 BBDST进化曲线

3.3 DST 工况实验

在实际应用中，锂电池的电流是复杂多变的，对电池的动态性能要求是严格的，也给复杂工况下锂电池SOC的估算带来了困难。为了验证本文算法提出的可靠性，用DST 工况进行验证，进行对比分析。实验结果如图6 所示。

图6 DST实验结果

由图6 得，改进的CEKF 最大误差最大为1.169 5%，比CEKF 少0.715 2%，比EKF 少5.140 5%；平均误差为0.683 6%，比CEKF 少0.540 1%，比EKF 减少了1.915 4%；均方根误差为0.755 9%，比CEKF 少0.540 3%，比EKF 减少了2.248 9%。由图6(b)的误差图得，改进的CEKF 各方面误差都小于EKF 和CEKF，且最大的误差都在2%以内，精确度比EKF、CEKF 算法更高，误差稳定性也比EKF、CEKF 好，可以更好地追踪SOC的理论值，更适合用于SOC的估算。

3.4 BBDST 工况实验

为了进一步验证该算法在实际应用中的有效性，进行BBDST 实验工况验证。BBDST 工况模拟的是北京公交车行驶过程中的起动、加速、减速等情况。SOC估算结果如图7 所示。

由图7 得，改进的CEKF 最大误差最大为2.381 9%，比CEKF 少了0.854 8%，比EKF 少了4.359 1%；平均误差为0.575 3%，比CEKF 减少了0.430 1%，比EKF 减少了1.553 9%；均方根误差为0.709 1%%，比CEKF 减少了0.374 2%，比EKF减少了1.745 6%。从图7(b)误差图得，改进的CEKF 比EKF算法的最大误差、平均误差、均方根误差都较小，且误差更加稳定，误差范围也都在2%左右。

图7 BBDST实验结果

4 结论

(1)本文以二阶Thevenin 等效模型为基础，采用自适应FFRLS 算法进行在线参数辨识，最大误差为2%，误差稳定在1.5%，实时跟踪能力较强，在线辨识效果较好;

(2)本文提出的GA 优化BP 算法对锂电池SOC的估算。通过遗传算法确定BP 神经网络权值的初值，可以大大减少迭代次数，增加神经网络的预测能力;

(3)通过实际锂电池测量的DST 和BBDST 工况实验，对比改进的CEKF 和EKF 与理论值的误差。结果表明，在两种工况下，改进的CEKF 比EKF 估算SOC的最大误差、平均误差都要小，且改进的CEKF 的最大误差不超过2.5%，整体误差也比EKF 的整体误差也要稳定，稳定性较好,即改进的CEKF 比EKF 能更加准确地跟踪估算锂电池的SOC。