基于资源调度和深度学习的5G多用户定位*

雷继兆,李潇楠,秦 浩

(1.中国航天科技集团东方红卫星移动通信有限公司,北京 100086;2.西安电子科技大学 综合业务网国家重点实验室,西安 710071)

0 引 言

随着第5代移动通信系统(5G)的发展，大量应用场景不断涌现，基于位置服务(Location Based Service，LBS)的技术[1]受到了研究人员的广泛关注。例如，在5G低时延高可靠、干扰异常复杂的场景下，每个用户的干扰情况主要取决于用户的位置分布以及资源调度，准确获取用户的位置信息将有助于基站在资源调度和数据传输过程中有意识地规避或者抑制干扰，从而降低传输差错概率，提高系统容量[2]。因此，基站准确获取用户的位置信息不仅是5G多种应用场景的基本功能需求，还能对基站的资源调度过程起到积极作用。

通常可以借助卫星来进行定位，如“北斗”卫星导航系统、全球定位系统等。该方法尽管定位精度很高，但是属于终端自主定位，与基站无关。通过基站与终端的信息交互，使基站能够获取终端位置也有着广泛的应用需求。现有技术主要分为两类：基于测距的定位技术与基于位置指纹的定位技术[2]。常用的测距技术包括基于到达时间(Time of Arrival，ToA)[4]、到达时间差(Time Difference of Arrival，TDoA)[5-7]、到达角度(Angle of Arrival，AoA)[8-9]等方法。文献[4]提出的基于能量值检测的最大似然估计方法联合了ToA和AoA技术，降低了对收发机时间同步的要求。文献[5]进而提出利用异步到达时间差技术来改进TDoA对时间同步的要求。此外，文献[9]提出了基于最小二乘的估计器，有效降低了AoA定位对设备精度的要求。上述基于测距的方法虽然在一定程度上减轻了收发机无法完全同步对定位精度的影响，但是测距信息的获取会消耗大量的计算资源，增加了计算复杂度，同时易受非视距环境的影响。另一类基于位置指纹信息的定位技术[10-13]则是先收集用户的位置指纹信息构建指纹库，然后将实时测得的位置指纹信息和指纹库进行匹配，从而实现定位。位置指纹信息主要由该位置处的信道状态构成。常见的位置指纹信息有信道状态信息(Channel State Information，CSI)和接收信号强度(Received Signal Strength，RSS)。其中RSS是对接收信号质量的粗粒度反映，无法精确反映信号的瞬时变化，而CSI是物理层的一个细粒度值，能够反映不同频率上的幅度增益和相位偏移，稳定性和灵敏度相比RSS更高，可以有效降低定位误差。文献[12]提出将每个用户的波束RSS作为指纹信息并利用机器学习手段对用户进行定位，实现了平均定位误差2 m的定位精度。文献[13]进一步结合5G毫米波与波束赋形技术将辐射到每个接收设备上的信号功率时延分布(Power Delay Profile，PDP)采集作为指纹并通过时间卷积网络的短序列，实现了室外平均定位误差1.78 m的定位精度。上述指纹定位方法均以物理层信息为输入，主要实现单用户定位。

与上述两类技术不同，本文提出了利用MAC层调度信息作为位置指纹，进而结合深度学习技术来实现基站快速估计用户位置信息。本文算法主要优势在于：一方面，利用调度过程中自然产生的诸如资源分配结果、真实传输后的调度效果等信息来完成定位，无需额外的信令开销，大大降低了数据采集成本；另一方面，利用深度学习挖掘多个用户之间的位置关系，从而可以同时实现多用户定位。本文所提方法既可作为现有定位算法的有益补充，也可指导基站在资源调度[14]过程中有意识地规避或者抑制干扰，提高系统容量。

1 多用户定位原理

假设有N个相邻基站记为集合B={b|b=1,2,…,N}，M个随机分布在N个基站下的用户记为集合U={u|u=1,2,…,M}，每个用户u根据自己的接收信号强度选择接入基站b(u)∈B。每个基站的可用资源块集合表示为C={c|c=1,2,…,G}，其中G为系统划分的资源块组(Resource Block Group，RBG)的总数。例如在FR1频段下，子载波间隔Δf=15 kHz，系统带宽5 MHz时，系统划分RBG的总数G=25；Δf=60 kHz，系统带宽100 MHz时，G=135。

在移动通信的下行调度过程中，基站以传输时间间隔(Transmission Time Interval，TTI)为调度周期，每个TTI都要根据用户业务请求以及信道质量信息按照某种调度算法为用户分配不同的RBG，常用的调度算法有最大载干比算法(Maximum C/I，MaxC/I)[15]、轮询算法(Round Robin，RR)[16]以及比例公平算法(Proportional Fair，PF)[17]等。调度算法针对用户u的资源分配结果可表示为

γu=(rbgu,1,rbgu,2,…,rbgu,G)T。

(1)

式中：rbgu,c∈{0,1}表示用户u对基站b(u)的第c个资源块的占用情况，0表示空闲，1表示占用。若某个TTI所有分配了资源的用户(下文简写为有效用户)记为集合A={a1,a2,…,am}，则该TTI的资源分配结果可表示为

R=[γa1,γa2,…,γam]。

(2)

由于每个TTI下有效用户数m不确定，因此不同的TTI中矩阵R的维度不同。

各基站根据以上分配结果，在相应的RBG资源上为每个有效用户传输相应的业务数据。由于信道条件不同以及相互之间可能存在的同频干扰，不同用户接收机处将测得不同的信道状态信息，数据传输可能成功或失败。如果用户本次数据传输能够正确解调译码，则其将向基站上报ACK=1，否则上报ACK=0。需要说明的是，在5G这种干扰受限系统中，数据传输失败主要由同频干扰引起，因此传输差错率反映了同频干扰的强弱。此外，用户还周期性地向基站上报当前时刻的信道质量指示(Channel Quality Indication，CQI)。CQI是用户信干噪比(Signal-to-Interference plus Noise Ratio，SINR)的某种粗量化映射，也能够反映信道质量的好坏和同频干扰的强弱。因此用户u该次资源分配的效果可表示为向量eu=(ACKu,CQIu)T，系统中所有有效用户的调度效果可表示为

E=[ea1,ea2,…,eam]。

(3)

综上所述，调度效果矩阵E在一定程度上反映了本轮数据传输中用户之间的干扰强度。换言之，ACK和CQI均为用户SINR的函数。

SINR是有用信号功率、干扰信号功率以及噪声功率相对关系的度量，在实际传输过程中，有用信号功率与干扰功率受路径传播损耗的影响，而路径传播损耗又取决于用户与各基站的距离。具体来说，基站b(u)下用户u的SINR可表示为

(4)

式中：Pu,k是用户u收到的来自基站k的功率；Pu=Pu,b(u)是用户u收到的来自基站b(u)的有用信号功率；Nu是用户u的噪声功率；Fu是与用户u占用相同RBG的相邻小区集合，即当基站b(u)下的用户u占用了rbgu,c的同时基站b(v)下的用户v也占用了rbgv,c。换言之，基站b(v)是对用户u有干扰的基站，所有对用户u有干扰的基站集合即为Fu：

(5)

式中：<γu,γv>=γuT·γv表示用户u与用户v占用相同RBG的个数。Pu,k可进一步表示为

(6)

式中：pk是基站k在每个RBG上的发射功率；du,k是用户u到基站k的欧氏距离；μu,k是干扰基站k分得的资源中与用户u占用相同RBG的总RBG个数，可表示为

μu,k=∑v:b(v)=k<γu,γv>；

(7)

ϑ(du,k)是基站k到用户u的路径损耗，可表示为

(8)

式中：d0为参考距离(单位m)，f为载波频率(单位Hz)，l为系统损耗，n为路径损耗指数，c是光速。

以上分析表明，用户SINR不仅取决于用户位置，还取决于资源分配结果R=[γa1,γa2,…,γam]。也就是说在各用户SINR已知的条件下，可以利用R来反推用户位置。然而工程实现中基站无法获得用户的SINR，尽管终端能够利用导频信号估计出SINR，但是终端上报给基站的是CQI，CQI只是SINR的某种粗量化。换言之，基站只能获取CQI，并不知道SINR的真实值。前文已经指出，用户SINR又进一步决定了资源调度效果E，或者说E在一定程度上反映了用户的SINR，其基本关系如图1所示。对于基站来说，资源调度效果E、资源分配结果R都是可以直接得到的信息，因此本文提出在SINR未知的情况下，通过E和R来估计用户位置的思路。基于该思路，第2节详细讨论用户定位方法。

图1 用户位置定位关系图

2 深度学习指纹定位技术

2.1 用户定位框架

对于基站来说，自身位置是已知的，只要求得用户与基站之间的距离ρ及相对角度α就可以定位用户的位置，如图2所示。由于上行方向上采用了时间提前量TA技术，所以每个用户的距离ρ对于基站来说都是已知的，在ρ已知的条件下获取角度α就成为定位用户位置的关键。接下来详细解释如何通过E、R来估计每个用户的角度α。

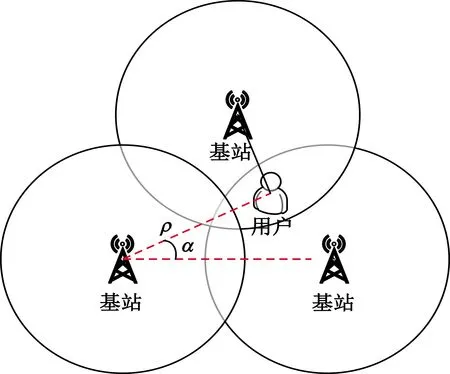
图2 用户定位示意图

由第1节所述的多用户定位原理可知，资源分配结果R、资源调度效果E等信息与用户位置之间存在某种高度非线性的关系，而深度学习网络具有自主学习能力，能够动态感知环境，且适应能力强，非常适合用来拟合上述非线性关系。与此同时，考虑到同一时刻下所有发起请求的用户的信息数据信息量大，数据维度较高，依靠传统的定位技术无法高效地解决这个问题。深度学习作为处理高维海量数据强有力的技术手段在图像、语音、视频、自然语言处理等领域都取得了巨大的成功，所以本文利用深度学习来解决用户定位问题，其基本框架如图3所示。首先建立用户定位数据集，并搭建深度神经网络(Deep Neural Network，DNN)，然后利用有监督的学习方法将数据集作为DNN网络的输入输出来实现用户定位。

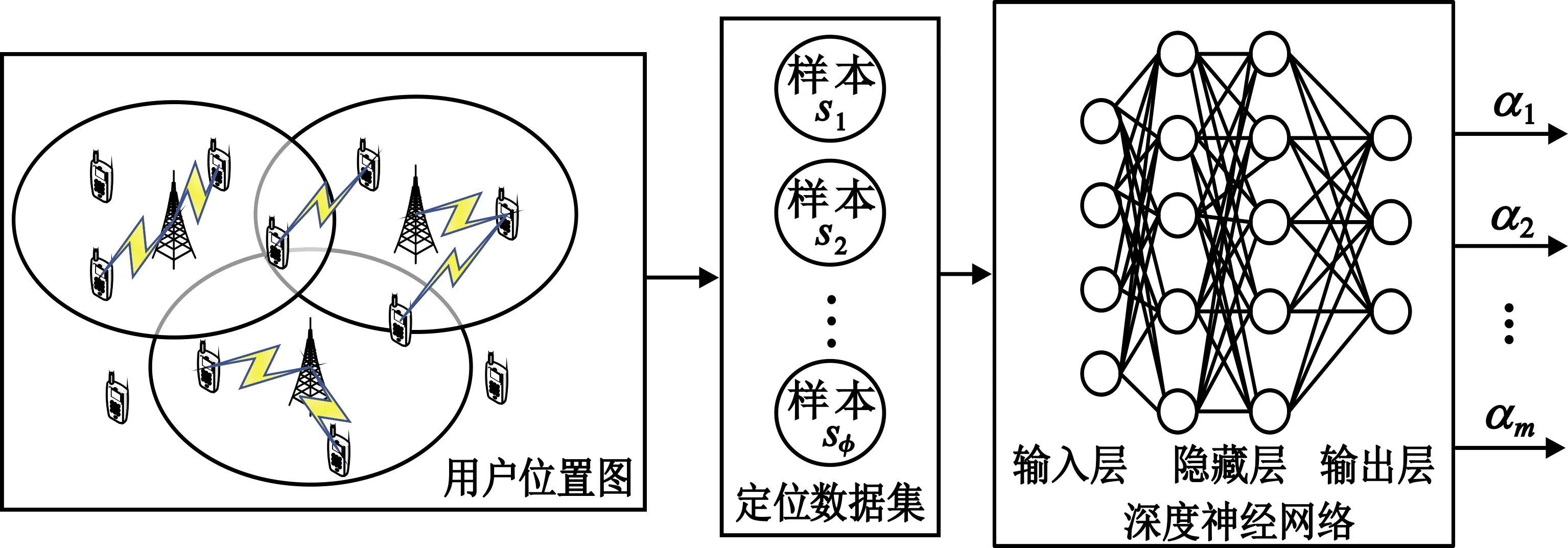
图3 用户定位框架

2.2 数据集建立

由图3可知，为了能够利用深度学习技术进行用户定位，首先要建立一个高质量的用户定位数据集，其建立过程主要包括三个步骤，如图4所示。

图4 数据集搭建流程图

首先利用网络级模拟器NS3搭建仿真场景。在设定的区域内，设置N个位置固定的基站和M个随机分布且以vmin～vmax的速度随机游走的用户，并设置基站按照某种调度算法为有业务请求的用户分配资源，尽可能真实地模拟用户和基站之间的数据通信过程。

之后在上述仿真场景下，提取每个TTI下的下行资源分配结果R、资源调度效果E、用户与基站的距离ρ以及用户的无线网络标识(Radio Network Tempory Identity，RNTI)和所属基站等信息作为位置指纹信息。在这个过程中，那些未分配到资源的用户不存在数据传输，既不会干扰其他用户，也不会受到其他用户干扰，也就说和E、R没有关系，这些用户对于定位算法来说是无效用户，因此需要在数据处理过程中将其去除。

此外，E是基站在执行了R后经过一段时延才得到，如图5所示，即在t时刻对用户的资源分配需要经过时延τ才能获取到用户的资源调度效果，因此在构造数据集时还需要将t时刻的资源分配结果R和t+τ时刻的资源调度效果E进行对齐操作。最终得到每个TTI下的用户定位特征信息，可用矩阵D∈m×z表示：

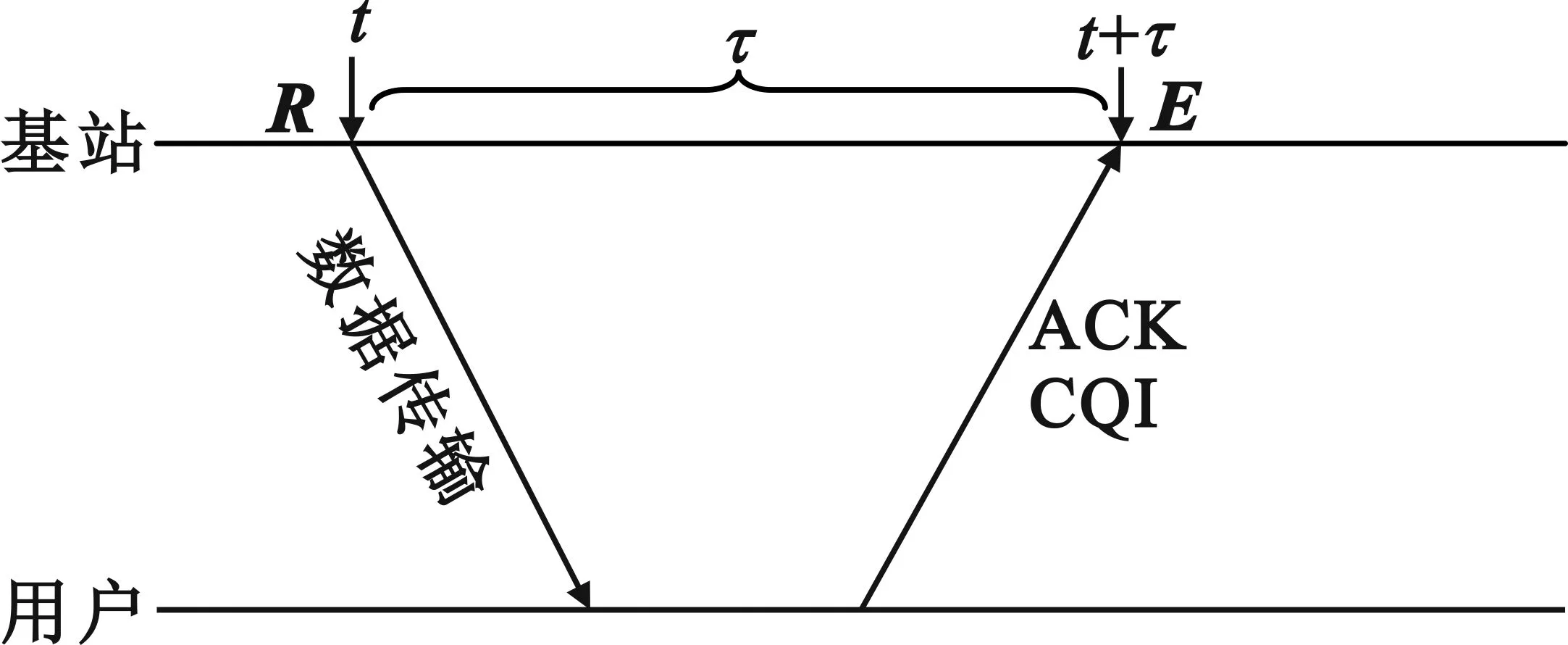
图5 对齐操作

(9)

式中：qm是由每个TTI下用户m的身份标识及其到接入基站的距离ρ构成的，可表示为

qm=(am,b(am),ρm)T。

(10)

然而，如果以上述特征信息D直接作为神经网络的样本特征建立数据集，样本质量并不好，主要是因为数据集样本之间存在较多的冗余信息，具体表现为：一方面，由于TTI的时间间隔很短，用户位置及有关特征变化并不明显，如果将每个TTI下的D作为一个样本，那么多个连续TTI对应的样本之间存在着强相关性，冗余信息太多；另一方面，用户一般只在某个区域内活动，这使得用户的位置信息仅集中在设定区域的某个范围内，从而导致提取出的用户位置信息存在相关性强，不具有普遍性。因此，为了解决数据样本中存在高度相关性的问题，本文针对上述两方面表现分别提出如下的数据去相关方法。

首先，将多个TTI的用户特征信息进行合并，作为神经网络的一个样本，以此来解决单个TTI信息作为样本时存在的强相关性。在合并多个TTI信息的时候，由于不同TTI发起请求的用户数目以及分配资源的用户数目是不同的，每个TTI的特征信息D维度是变化的，为此本文将每个样本的维度固定为M，然后将n个TTI的特征信息进行合并得到单个样本的特征矩阵F∈M×z：

F=[Dt1T,Dt2T,…,DtnT]T。

(11)

其中超过M的部分直接去除。对于每个样本的标签的处理也是通过仿真场景中获取得到用户和基站的坐标信息，然后将其转换为以基站为中心的极坐标形式后提取角度α。可用矩阵L∈M×z来表示上述每个样本特征矩阵所对应的标签：

L=[lt1,lt2,…,ltn]T，

(12)

l=(α1,α2,…,αm)。

(13)

式中：l为一个TTI时刻下所有有效用户的角度向量。所以用户定位数据集中的一个样本即可用符号S=[F,L]表示。

其次，为了解决由于用户运动区域较小带来的数据相关性和不具有普遍性的问题，本文搭建了W个用户初始分布不同的仿真场景，保证用户在设定区域内的位置分布足够均匀，进而分别使用前述方法采集样本构成数据集。

最后，利用数据去相关在上述W个场景中共取φ个样本，建立用户定位数据集J={S1,S2,…,Sφ}用于训练。

2.3 神经网络搭建

DNN网络结构由多层全连接层构成。全连接层(FC)是将每一个结点与上一层的所有结点相连，用来把上一层提取的特征综合起来，达到预测的目的。单层FC层有时无法解决非线性问题，而FC层数越多，每层神经元个数越多，非线性表达能力越好，模型的学习能力越强，但是也容易造成过拟合。同时FC中会设置激活函数来增加模型的非线性表达能力，常见的激活函数有Relu、tanh与sigmoid函数。其中tanh函数与sigmoid函数容易在输入过大或很小出现梯度消失问题，而Relu则能够较好解决梯度消失问题，且计算简单，收敛较快。本文采用Relu，即

(14)

为了提高预测准确率，本文采用的损失函数是均方误差MSE，如下式所示：

(15)

式中：X为网络的输入，f(X)为网络的输出(预测的用户角度)，Y为实际的输出(用户的真实角度)，ω为样本个数。

最后通过调节学习率、神经元个数、网络层数等参数来提高模型的准确率和泛化性。

3 实验与分析

3.1 实验参数设置

根据第2节提出的深度学习指纹定位技术，本文利用NS3网络模拟器搭建了移动通信仿真场景，建立数据集，并通过深度学习DNN网络进行用户定位的实验。实验过程仿真参数设置如表1所示。

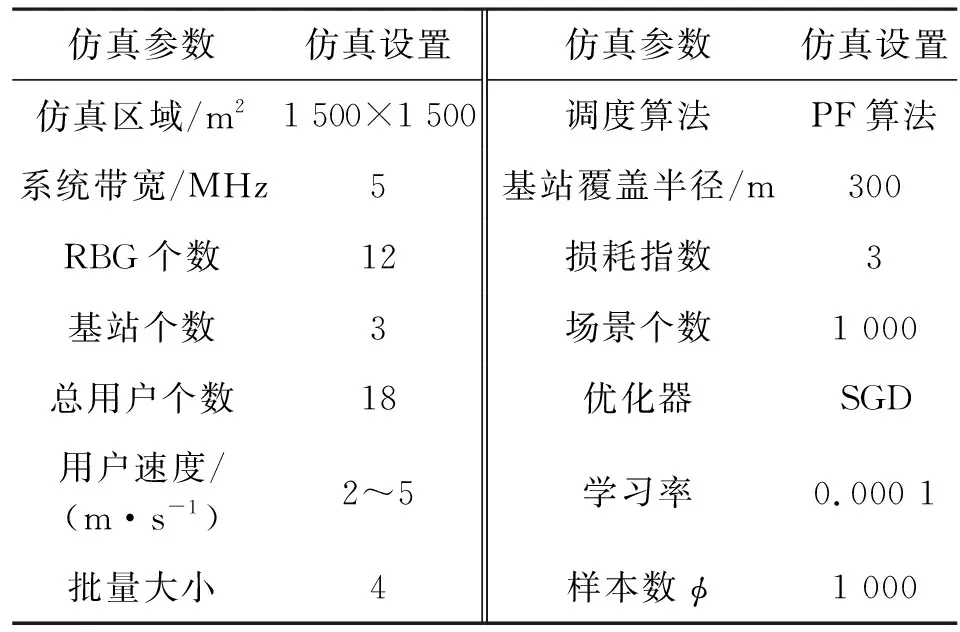
表1 仿真参数设置

3.2 实验结果

为了优化网络模型性能，提升定位精度，我们对网络参数的设置进行了分析，将DNN输出的用户位置和实际用户位置之间的欧氏距离作为衡量定位精度的标准。

首先，对网络层数和神经元的个数分别进行对比实验，结果如图6所示。当各层神经元个数均为1 024时，对比不同的网络层数可以看出，4层的网络结构明显优于其他网络层数；在网络层数同为4层时，每层1 024和2 048个神经元条件下的准确率几乎相当且都明显优于每层512或256个神经元的情况，但是2 048个神经元的网络计算复杂度更高。基于表1的参数设置，结合定位准确率和网络复杂度考虑，在后续实验中，本文采用了4层全连接、每层1 024个神经元的DNN网络结构。

(a)不同网络层数的准确率对比

图7分析了不同学习率下的定位精度及模型学习速度，可以看出，学习率为10-4的曲线在迭代8 000次后开始趋于稳定，学习率为10-5的曲线在迭代1 000次后开始趋于稳定，学习率为10-6的没收敛，明显看出10-4学习率下具有更快的收敛速度。同时，该曲线有着较高的准确率。该曲线在学习过程初期出现明显振荡现象，在8 000次之后，振荡减轻，说明此时的网络模型已有较好的学习能力。

图7 不同学习率下的定位准确率比较

本文采用SGD作为网络优化器，将数据集中20%的数据作为验证集，来评估网络模型的收敛性，实验结果如图8所示。在9 000次迭代之后，网络模型基本收敛，验证集在7 200次和10 900次有轻微的振荡。此外，本文分析了在不同精度下的用户定位准确率，如表2所示。在定位精度10 m时，所提方法可以实现90%以上的定位准确率。

表2 不同的定位精度下用户的定位准确率

图8 网络模型收敛性分析

本文方法与文献[13]的算法采用了完全不同的机理，定位目的也有所不同。文献[13]利用物理层的PDP信息作为定位依据，平均定位误差在1.78 m，主要用于室外单用户的精准定位。而本文则利用资源调度信息，不需要占用额外的时间和计算资源即可完成多用户的同时定位，获得小区内用户位置的整体分布，可主要用于预测业务热点，相应指导基站在资源调度过程中有意识地规避或者抑制干扰，从而提高系统容量。

4 结 论

本文提出的利用MAC层调度信息的深度学习指纹定位技术，一方面可实现基站在定位精度10 m内对多用户定位的准确率达到90%以上的效果，可为现有定位算法提供有益补充；另一方面将有利于基站在干扰异常复杂的场景下合理高效进行资源调度，从而提高系统容量。因此，本文算法在实际工程应用中有着独特的应用价值，同时本研究内容与结论可为今后优化5G空口资源调度问题提供一定的借鉴和参考。