一种“北斗”三号精密单点定位的三频模糊度解算方法*
劳源基,熊泽凯,王靖君,覃团发
(广西大学a.计算机与电子信息学院;b.广西多媒体通信与网络技术重点实验室,南宁 530004)
0 引 言
目前“北斗”卫星导航系统(Beidou Navigation Satellite System,BDS)已经开放了多频信号的公开授权服务[1-2]。随着多频信号的播发,三频观测值可以通过组合形成具有波长较长、电离层延迟较小和观测噪声小的三频最优组合,进而提高了模糊度解算(Ambiguity Resolution,AR)的成功率,极大地推动了精密单点定位(Precise Point Positioning,PPP)技术的发展。精密单点定位被广泛应用于各个领域,如地球物理、大地测量、气象领域以及高精度导航等领域[3]。在相对定位中,用户与基准站之间的基线长度是制约定位精度和应用的关键因素。在单个接收机方面,PPP不需要基准站,更加灵活,得到了广泛的应用。在进行PPP时,载波相位观测值被用于实现精密定位,整周模糊度是载波相位观测值的主要参数,因此在进行PPP之前需要得到准确的整周模糊度。文献[4]提出了经典的三载频模糊度确定法(Three-Carrier Ambiguity Resolution,TCAR),通过“层叠”关系直接对模糊度进行解算,省略了模糊度解算中繁琐的搜索空间,获得了较好的解算效果。文献[5]提出了级联模糊度确定法(Cascade Integer Resolution,CIR)。文献[6]对经典TCAR算法加以改进,提高了窄巷模糊度的固定准确度。文献[7]分析了“北斗”三号不同频点的不同组合。文献[8]通过聚类算法对“北斗”三号卫星导航系统(Beidou-3 Navigation Satellite System,BDS-3)的组合分析,比较得出适用于不同场景下的三频组合。文献[9]从收敛时间的角度上分析了AR与PPP的定位精度的影响。文献[10]参考全球定位系统(Global Positioning System,GPS)PPP单天解,阐述了BDS PPP-RTK AR对定位的可靠性的影响。文献[11-12]从正确率和时间出发,阐述了融合GPS/BDS进行PPP AR的优势。文献[13]提出了三频AR方法的意义和面临的问题挑战。文献[14]通过实测的“北斗”系统三频观测数据,验证了基于原始观测模型的三频PPP AR的性能。
本文在传统Boot-strapping方法的基础上加以改进,提出了一种改进的三频模糊度解算方法。选用BDS-3系统性能更好的B2a信号取代B2I信号,与B1I、B3I组成的三频信号观测值组合,通过比较选择波长长、各误差项都较小的最优三频观测值组合,在AR的过程中还加入了额外的伪距组合来减弱电离层的影响。相比于传统方法,改进方法的窄巷组合AR有着更高成功率和更准确的固定值。
1 传统Boot-strapping方法
1.1 “北斗”三号三频线性观测值组合
2020年6月23日,随着“北斗”三号第55颗GEO卫星的发射,我国BDS-3系统全面组网成功。目前BDS-3系统已经可以提供5个信号的公开授权服务,分别是B1I(1 561.098 MHz)、B1C(1 575.42 MHz)、B2a(1 176.45 MHz)、B2b(1 207.140 MHz)和B3I(1 268.520 MHz),其中包括公开服务的新信号B1C、B2a和B2b信号。
全球卫星导航系统(Global Navigation Satellite System,GNSS)导航定位使用的频率由基准频率组成。设“北斗”系统的基准频率是f0,则每个频点的频率可以表示为fi=ai·f0。BDS-3三频信号组合对应参数如表1所示。
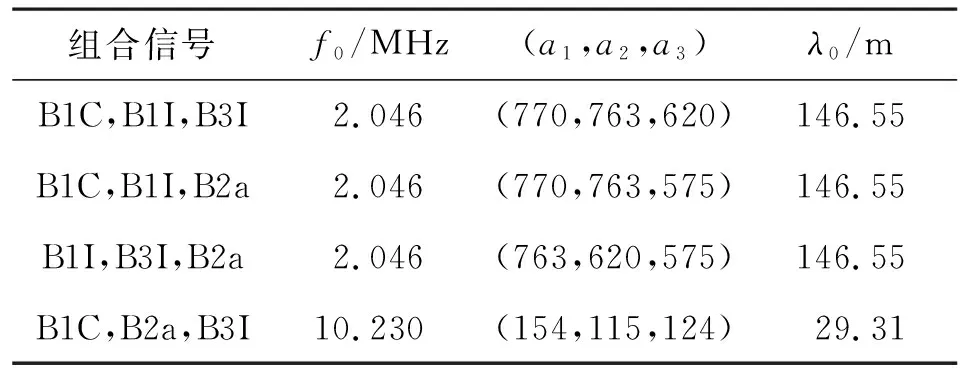
表1 BDS-3系统三频信号组合对应的参数
本文优选B1I、B3I、B2a三个信号进行组合,可以得到具有虚拟频率的观测值组合。f1、f2、f3分别是组合信号中的三个频率,且f1>f2>f3,这里分别对应BDS三个载波频点B1I(1 561.098 MHz)、B3I(1 268.520 MHz)和B2a(1 176.45 MHz)。因此,多频伪距观测值和载波相位观测值表示如下:
Pi=ρ+γiδI1+ei,
(1)
Li=ρ-γiδI1-λiNi+εi。
(2)

多频载波相位观测值还可以表示如下:
Li=λi·φi=ρ-γiδI1-λiNi+εi。
(3)
式中:单位为周的载波相位观测值由φi表示。假设组合系数分别为m、n、k,且均为整数,分别对应f1、f2、f3,φmnk(单位周)和Lmnk(单位m)均表示三频载波相位组合观测值,则可推出三频载波相位组合观测值如下:


(4)
式中:Nmnk表示三频载波相位组合的模糊度,
Nmnk=m·N1+n·N2+k·N3。
(5)
当用组合系数m、n、k分别对方程(1)和方程(2)进行整理,可以将“北斗”三频伪距和载波相位观测值的线性组合分别表示如下:

ρ+γmnkδI1+emnk,
(6)

ρ-γmnkδI1-λmnkNmnk+εmnk。
(7)
式中:emnk表示三频组合伪距的测量噪声,εmnk表示三频组合载波相位的测量噪声。假设三频组合波长为λmnk,组合频率为fmnk。另外,当组合系数满足m+n+k=1时,Nmnk可以保持整数特性,与频率无关的对流层项在组合后不发生变化。其中:
fmnk=mf1+nf2+kf3=(ma1+na2+ka3)f0,
(8)
(9)
γmnk是组合信号相对于频率f1的电离层延迟系数,表示如下:
(10)
在实际环境中,卫星信号传输产生的误差主要来自电离层和对流层,还会产生多径效应。在精密单点定中可以通过观测值线性组合来削弱电离层一阶延迟,而高阶项远小于一阶延迟。对流层延迟的大小与频率无关,主要由干、湿两个分量构成[15]。多径效应使得信号观测存在一定的偏差。削弱多径效应的常规操作包括选择较大的卫星高度角、软件和硬件方法和较好的观测环境。在PPP中,可以假定多径效应为随机噪声,因此,本文将测量噪声和多径效应合到一起来分析。
在研究中假设B1、B2和B3的伪距测量噪声相同且相互独立,载波相位噪声也是如此,即σL1=σL2=σL3=σL,σP1=σP2=σP3=σP。根据经验,假定在相同环境下令载波相位噪声和伪距噪声分别为σL=0.004 m,σP=0.6 m。根据传播定律,载波相位和伪距组合观测值的方差分别为

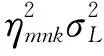
(11)
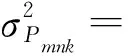

(12)
式中:ηmnk为噪声系数,表示为
(13)
1.2 Boot-strapping方法的步骤
在传统Boot-strapping方法中,整周模糊度的解算主要是通过从组合波长较长到组合波长较短的顺序逐级解算。由于大多数的线性组合的波长都较短,各项误差较大,不能用于AR。因此,在Boot-strapping方法中选择最优的线性组合是AR的关键。
通常,Boot-strapping方法在第一步中选择两个频率更接近的组合解算超宽巷(Extra-wide-lane,EWL)组合,然后通过构建 Hatch-Melbourne-Wubbena(HMW)组合解算出EWL的模糊度浮点估计值。在解算过程中,HMW组合可以有效地削弱电离层延迟误差和几何参数的影响,得到模糊度浮点估计值后取整得到整周模糊度,再用整周模糊度对EWL组合进行更新。第二步将前面所得到的EWL组合看作是更加精确的伪距,对宽巷(Wide-lane,WL)组合进行AR,WL模糊度的解算是通过第二接近的两个频率的载波组合形成,选择第二最长的组合波长,用于计算WL组合的模糊度。第三步把已经进行AR的WL组合作为更加精确的伪距,对窄巷(Narrow-lane,NL)组合进行AR。在传统Boot-strapping方法中,NL组合直接采用波长最长的原始观测值,再以与第二步相同的方式舍入得到整周模糊度。成功固定三个组合的整周模糊度后,建立三个线性无关的一阶方程,进而恢复出原始的模糊度。最后可以把恢复的模糊度作为已知量代入到原始的定位模型中,以得到定位结果。Boot-strapping方法是基于一组选定的原始观测值的线性组合,与其他解算方法相比,降低了计算的复杂度。
2 改进的三频模糊度解算方法
本文根据传统的三频AR方法(TCAR、CIR、Boot-strapping、经验理论),提出了一种改进的可用于BDS-3 PPP的三频AR方法。不同于传统算法的EWL-WL-NL,选择了EWL-EWL-WL-NL的解算策略。
2.1 第一个超宽巷(EWL1)组合的模糊度解算
通常,在第一步中选择两个载波相位观测值解算EWL1组合的模糊度。这两个观测值选择的标准是从两个频率更接近的频点中选出。对于“北斗”三号,载波B2a和B3I的频率更接近。此外,如表2所示,组合(0,1,-1)的波长较长,电离层延迟系数和噪声系数较低。因此,选择(0,1,-1)作为EWL1组合,伪距组合选择(0,1,1)。

表2 BDS-3三频组合的特征值
几何参数不随频率变化而变化,所以通过伪距和超宽巷的联立来消除,即选择HMW组合来消除。由HMW组合导出的EWL1的模糊度表示如下:
NEWL1=N2-N3=

(14)
式中:P2、P3分别是载波B3I、B2a的伪距观测值,L2、L3分别是载波B3I、B2a的载波相位观测值,λEWL1是EWL1组合的组合波长。由表2,γ(0,1,1)+γ(0,1,-1)=0,大大削弱了电离层延迟,且组合波长达到了3.256 1 m,对于模糊度解算有很大帮助。因为原始载波相位的噪声为0.004 m,远远小于组合波长,显然组合噪声可以忽略。其余的误差如对流层延迟的湿分量、卫星时钟误差,已经通过精确的模型来消除。然后,从浮点解中直接取整,得到EWL1组合的模糊度整数值,可以表示为
(15)
2.2 第二个超宽巷(EWL2)组合的模糊度解算
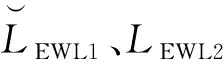
(16)
(17)
式中:j1、j2、j3、j4、j5分别为权重系数。令j5=1,式(17)应满足以下约束条件:
(18)
式中:σL=0.004 m;σP=0.6 m;h为自适应权因子,
(19)
按式(19)能选出用于解算EWL2的模糊度的h,并且成功率最高。再由式(17)求得EWL2的模糊度,最后舍入得到整数解,表示为
(20)
2.3 宽巷(WL)组合的模糊度解算

(21)
式中:WL组合模糊度需要得到准确的整数值,故系数a、b均为整数,根据实际应用由如下公式确定:
(mWL,nWL,kWL)=a(mEWL1,nEWL1,kEWL1)+
b(mEWL2,nEWL2,kEWL2)。
(22)
由式(22)可得到系数a、b的值,代入式(21)求得WL组合的整周模糊度为
(23)
2.4 窄巷(NL)组合的模糊度解算
在传统Boot-strapping方法中,通常采用(0,0,1)作为窄巷组合。不同于PPP,相对定位能够通过做差的方式来除去大多数误差。然而,在PPP中,传统NL组合相比于前两种组合电离层延迟误差和测量噪声较大,无法预先消除的这两种误差会严重制约着AR的成功率。因此,选择组合系数尽可能小但仍然具有相对较长的波长和较低的噪声的组合。根据表2,选择(4,0,-3)作为NL组合,在解算时还引入(1,0,0)作为伪距组合。因此,考虑到几何参数和电离层延迟参数的影响,NL组合模糊度可以由伪距观测值和WL模糊度推导出来,表示为
(24)
式中:系数z1、z2应满足
(25)
通过系数z1、z2适当取值,消除电离层延迟。最终可以精确地对NL组合进行AR,得到的模糊度由式(26)取整舍入。
(26)
2.5 原始模糊度解算
固定了这三个组合的模糊度后,根据组合系数,B1I、B3I、B2a的整周模糊度即N1、N2、N3,能够从式(27)中恢复过来。
(27)
求解式(27)可以得到唯一解。在成功固定模糊度以后,可代回载波相位原始观测方程,提高观测值精度,从而得到可靠的PPP定位结果。
3 实验分析
采用北京合众思壮生产的 Phantom 系列的 P40 板卡来对“北斗”三号卫星信号进行静态接收。实测的静态数据接收时间为2021年2月16日 20:00到2021年2月17日 20:00,为了数据准确性,去掉前4 h和后2 h的数据。接收地点在广西北海,数据的采样间隔为30 s。接收的静态卫星数据来自BDS-3的第27和第28号中地球轨道(Medium Earth Orbit,MEO)卫星。
3.1 不同组合的成功率
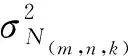
假设通常情况下噪声满足正态分布,那么这三种组合的模糊度同样满足正态分布,即N(m,n,k)~N(γ(m,n,k)δI1,σN(m,n,k))。因此,为了验证改进方法的优劣,用组合AR的成功率P作为评估标准,用高斯概率密度函数表达如下:
(28)
式中:u是模糊度浮点值相对于模糊度参考值之间的偏差,μ和σ分别表示u在周期内的标准差和方差,-0.5~0.5是AR成功率的理论区间。在相同组合中,模糊度固定成功率的高低会受到来自电离层和噪声的制约。
组合模糊度参考值可以用总历元求和取整数均值,如式(29)所示:
(29)
式中:i表示总的历元数,t表示当前历元,Nt(m,n,k)表示在i历元处模糊度的浮点估计值。
EWL、WL、NL和传统方法下NL模糊度解算成功率如图1所示,可以看到在不同载波相位噪声下相同组合的成功率不相同。从图1还可以看出,AR的成功率会随着电离层延迟的增大而减小,对于相同组合载波相位噪声大的曲线下滑快于载波相位噪声小的曲线。如图1(c)所示,当电离层延迟达到0.6 m时,改进方法的NL组合AR的成功率才会从100%开始下降,即使在σL=0.04 m的嘈杂环境下。如图1(d)所示,当电离层延迟大于0.16 m,即使在σL=0.004 m的环境下,传统方法的NL组合在相对较好的环境下AR的效果很差,其固定成功率下降到零。结果表明,改进方法的AR成功率在电离层延迟较小时保持着较高的成功率;在相同噪声环境下,传统方法NL的AR成功率随着电离层延迟变化较为敏感。

(a)改进方法EWL组合成功率
3.2 模糊度残差

(a)改进方法EWL组合模糊度残差
图3表示的是第28号MEO卫星的EWL、WL、NL和传统方法下的NL组合模糊度的残差,曲线的结果与第27号MEO卫星相似,并且改进方法的NL组合模糊度的残差比传统方法的NL组合取得的效果更好。

(a)改进方法EWL组合模糊度残差
4 结 论
本文选用性能更好的B2a信号取代B2I信号,获取BDS-3由B1I、B3I、B2a组成的三频信号组合,在此基础上对在传统Boot-strapping方法进行改进,提出了一种改进的三频模糊度解算方法。通过比较选择具有波长较大、电离层延迟较小以及测量噪声较小的三频观测值组合。在电离层延迟不能忽略时,通过引入额外的伪距观测量组合来消除解算组合模糊度过程中的电离层和几何参数的影响。实验表明,所提方法与传统方法在完成一次模糊度解算的时间上相差无几,但是相比于传统方法,改进方法可以确保AR有更高的成功率,并且对于窄巷模糊度解算的精度有显著提升,模糊度固定的估计值能够达到3周以内,相比于传统窄巷组合的模糊度解算方法,模糊度固定估计值精确了3周左右。

