基于改进CRITIC的灰色关联网络安全态势评估方法*
陈 龙,吕 磊,杨旭东
(国网四川省电力公司信息通信公司,成都 610015)
0 引 言
如何针对电力网络进行准确高效的网络安全态势评估是目前网络安全领域学者们探究的前沿热点。随着国家电网体系的不断完善,为了实时监控电网系统的状态,对当前电网安全态势进行评估显得尤为重要。
网络安全态势感知[1]是以态势评估为核心,通过提取网络安全要素信息[2-3],建立态势评估技术模型。该领域的先驱者Bass[4]通过给出最初的网络安全态势评估框架,并运用一系列的数据处理方法将网络安全与态势感知的概念相结合,虽然其给出了感知框架但并没有给出具体的实现。后续的学者们根据这个框架进行了大量的探索,研究方向主要有三大类,分别为基于数学模型、基于概率知识推理和基于模式识别。
章宜玉[5]提出了一种主客观相结合的方式,将主观权重群组层次分析法与客观权重熵权法相结合,提出了一种二级模型,但是并没有考虑到熵权法所存在的信息利用不完善的缺陷。吴琨等[6]提出了一种集对分析评估方案,以解决网络中多种数据源相互交织引发的不稳定的问题,取得了较好的评估效果,但集成分析法所存在的缺乏验证性和标准性的固有特点并没有得到解决。Wang等[7]通过在评估中加入概率图例模型提高了模型的可验证性,但是在产生条件概率时,需要过多依赖专家经验。李鹏[8]基于层次化模型和D-S证据理论引入了时间参数来进行改进,取得了一些进展,但同样是过多依赖专家经验。汤永利等[9]通过使用误差逆向传播的前馈神经网络来解决过度依赖人工前导概率分配的问题,在一定程度上降低了人为因素对结果的影响,但是需要使用大量的训练样本,加重了网络计算负担。Jia等[10]使用机器学习提取实体并构建本体以获得网络安全知识库,加入了路径排序算法来推导新规则并运用斯坦福命名实体识别器(Named-entity Recognition,NER)训练提取器以提取有用的信息,但当证据出现冲突时准确性会受到影响。范渊等[11]引入模糊粗糙集技术,解决了粗糙集的固有缺点,即损失精度,其与基于概率和知识推理不同,该算法不依赖于证据理论,简化操作,准确性进一步提升,是一种模式识别[12]算法。
灰色关联算法是模式识别中的一种,本是用于衡量待评估指标与最终评估结果的关联度大小问题,并针对待评估指标进行关联度排序,其算法简单、易于实现,并且不需要针对样本进行过多的训练。李玲等[13]针对网络中的攻击要素,使用灰色关联分析算法进行关联分析,并根据得到的关联序列对每一个要素进行排序,并利用综合得分评估整体网络安全态势,算法简单容易实现,但是并没有考虑到指标间的重要程度。汪材印[14]将灰色关联分析与支持向量机相融合用于网络安全态势评估中,通过对大量数据的训练,提高了评估准确性,但同样没有考虑到评估指标的重要程度,并且针对数据的训练量较大。王磊等[15]将CRITIC(Criteria Importance Through Intercriteria Correlation)法引入灰色关联评价模型中,完善了指标的权重关系,但是并没有考虑到主客观指标赋权平衡与灰色关联用于定量评估的问题。
将灰色关联算法用于定量的评估时,由于其选取的序列单一,所得到的评估结果相应也较为单一片面。结合以往众学者的研究成果,针对其在网络安全态势评估中的缺陷,本文提出一种基于优化CRITIC的改良灰色关联网络安全态势评估算法,通过引入信息熵与变异系数来改变CRITIC法原有的信息量残缺、主客观不平衡的问题,并通过优差序列的形式对原灰色关联法进行改进,解决其序列单一、量化标准不完善的问题,最终将两者结合进一步完善灰色关联算法并用于网络安全态势评估,通过在公开数据NSL-KDD与实际电网数据集上进行充分的对比测试验证了本文所提出方法的可行性与有效性。
1 基于改进CRITIC的灰色关联网络安全态势评估模型
1.1 灰色关联分析
灰色系统[16]最初是由控制科学与工程的教授邓聚龙针对白色系统与黑色系统而提出的用于数据分析的概念。黑色代表对内部信息毫无了解,白色是充分掌握信息,灰色介于这两者之间。灰色系统理论提出了灰色关联[17]的概念,即在一个灰色系统中,目标参数受到其他待评价指标的影响程度,是一种多因素的统计分析方法。此方法通过对动态过程发展态势的量化分析,求出母序列与各比较数列之间的灰色关联度,从而得出关联序。其关键步骤如下:
(1)确定反应系统特征的母序列或者参考序列,一般取自研究的某一因素与其他因素之间的关系。
(2)变量的无量纲化。系统中各个因素的数据由于其量纲不同,可能会出现大小相差过大的情况,难以比较和得出的结果有失准确性,因此为了保证数据的一致性和结果的可靠性,在进行分析时一般都要进行数据的无量纲化处理。
(3)求参考序列与待评估序列中差值中的最大最小值,并由此计算每待评估序列的关联系数值。
(4)计算关联序并根据关联序排序得出待评价对象与参考序列的关联度大小来评价对象的优劣程度。
1.2 Critic客观赋权法
CRITIC法是由Diakoulaki等[18]在1995年提出的一种基于指标变异性与关联性的客观权重赋权法,是一种客观科学的评价方法,并具有如下特性[19]:
对比强度:以标准差的计算方式来衡量指标在不同待评价序列中取值差距的大小,与权重的分配成正相关。
指标之间冲突性:用皮尔森(Pearson)系数进行表示,若两个指标之间皮尔森系数越高,反应的信息重复率越高,此时在分配权重时应给予较小的权重,即皮尔森系数与权重分配成负相关。
其核心步骤如下:
(1)构建原始指标数据矩阵并进行数据无量纲化处理。与灰色关联法相同,即消除因量纲不同对计算过程和计算结果的影响。与灰色关联法不同的是,CRITIC法并不推荐使用标准化处理,因为经过标准化处理后的数据标准差全部为1,而CRITIC法是需要标准差来对表现数据的波动性。因此针对CRITIC法,采用的是正向化或者是逆向化处理。
(2)求解指标变异性与冲突性,即标准差与皮尔森系数。
(3)计算待评估指标的信息量与权重。
1.3 基于改进CRITIC的灰色关联分析法模型
本节主要讲解本文核心算法的改进方式与步骤,通过对数据的统一预处理,减少CRITIC与灰色关联法不同量化标准所需的计算量;其次在CRITIC客观赋权法中结合优化后的熵权法使得CRITIC信息量更加全面,为了突出决策者的主观意志与对某些指标的重视程度,通过引入变异系数的方式来平衡指标;最后借助于TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)的思想,对灰色关联分析进行优差序列的改进并引入改进后的CRITIC法来突出指标之间的重要程度从而客观衡量某一事件对整个系统的影响。基于此,通过计算时序内事件的总影响程度来得到时序内系统网络安全态势值。
1.3.1 数据预处理
假设有n个待评价样本,p项评价指标,构建原始数据矩阵:
之前的方法中,CRITIC法与灰色关联的无量纲化处理并不一致,为了减少计算量同时满足CRITIC法的计算,本文统一采用min-max归一化[20],即
记归一化后的数据矩阵为x′,同时用于后续CRITIC与灰色关联分析法的计算。
1.3.2 基于变异系数的改进CRITIC法
传统的CRITIC客观赋权法综合了指标的变异性与冲突性,但是并没有考虑到指标信息的混乱程度,因而其所表现的信息具有残缺性与不完整性。为了弥补CRITIC法的这一缺陷,通常的做法是分别计算CRITIC的权重C1与熵权法的权重C2,按照式(1)来进行最终权重的计算[20]:
W=βC1+(1-β)C2。
(1)
式中:W为最终的权值,β通常取值0.5。这样的做法有一定的合理性,但根据目前的研究来看,没有人来界定β的合理取值,因此这样的方式虽然有合理性但是并不能让人充分信服。本文通过在中间过程加入熵权法的混乱程度的计算来达到两者的合理结合,并且在后续过程通过增加变异系数来进行,减少传统主客观方法相结合的工作量,使其能够表达的信息更加全面,并且更加符合决策者对某些指标的重视程度。
Step1 计算指标变异性Sj。
根据式(2)得到数据变异性(标准差)Sj:
(2)

Step2 计算指标冲突性Rj。
根据式(3)得到数据的相关系数进行表示:
(3)
式中:rij表示评价指标i与j之间的相关系数,Cov(i,j)为待评价指标i和j的协方差,Var[i]为指标i的方差,Var[j]为j的方差。待评估指标相关系数越大,其所表达的信息重复率就越高,此时要平等地分配权重显然不符合实际,应减少权重的分配。因此利用式(4)来表示指标的冲突性:
(4)
Step3 计算激活信息熵与改进后的信息量。
在此步骤中,针对CRITIC法中信息量涵盖不完全的问题,本文引入优化后的信息熵[21]来表现数据的混乱程度,进一步丰富CRITIC法中的信息量,以解决其信息残缺的问题。
计算第i个对象的第j项评价指标出现的概率pij:
计算第j个指标的信息熵ej:

考虑到变异数据对信息熵的影响,本文采用改进后的激活熵[22],即
根据信息熵本身所具备的特点——信息熵与权重的分配成负相关[23],因此在加入到CRITIC法的时候,采用式(5)的形式:
(5)
将信息熵引入到CRITIC可以充分考虑到指标的离散性、变异性与冲突性。针对乘法与加法模型,因加法模型是假定因素之间是独立存在的,乘法模型是假定因素之间对最总结果是相互影响的,结合原CRITIC法采用的乘法模型,此处将信息熵引入CRITIC中同样采用乘法模型,采用式(6)来对CRITIC方法进行改进:
Ij=Sj·Ej′·Rj。
(6)
式中:Ij表示融合后第j个指标所含的信息量。
Step4 通过变异系数改进权重。
针对Step 3中的信息量,通过占比来计算每个待评估指标的初步权重:
(7)
式中:wj为第j个指标的初步权重表现,即根据每个待评价指标所包含信息量占比来初步确定权重。
通过上述步骤初步确定了指标权重,但是无法体现出指标发生波动后对权重的影响与决策者的意愿。为了改善这一状况,本文方法在原有的初步权重上引入了变权理论[24]来对上述权重进行变权处理。文献[25-26]研究表明,鉴于指数状态变权向量具有拟合效果和容易扩展构建等特点,因此本方法使用指数型状变权向量,构建方式如式(8)所示:
(8)
式中:α为惩罚水平,β为否定水平。通过对指数型变权的分析,即α与β的取值与最终总结果密切相关。
针对α的取值,由于指数型的特征,-α(Wj-β)的值越大,最终结果越小,会将原有的指标进行严重地稀释,因此,在选取α值时应尽量控制在(0,1)之间,使最终结果偏离原值幅度不大。
针对β的取值,其值的大小关系每一个权重的分布,因此应根据实际条件进行取值,针对较大原权重,-α(Wj-β)结果小于0,经过变权后会相应地提高其权值,原权重比β小的,-α(Wj-β)结果小于0,经过变权后,会惩罚性地降低权值。但我们的目的是为了提高某些因素的权重,并不希望每个因素都趋于一致,因此要严格控制权重的上升与下降,即采用惩罚性变权,将希望变权的因数用β进行限制,并规定其作用域在小于β的范围内。
称改进后的权重算法为VAR_CRITIC算法。
1.3.3 改进的灰色关联分析法
在常规的灰色关联分析方法中,参考序列一般取自被比较的对象,且一般只有一组。在用于态势评估时,并没有一个非常准确的指标去评判本次结果,因此在原方法中选取序列时,通常取数据样本中的最优状态为参考序列,通过每个指标与该最优状态的关联性来突显当前的网络安全态势值,这样得到的结果即是与当前最优情况的关联度大小,通过对最优状态的评估来评估每一个待评估样本的分数。
但只有这样一组优序列所得到的结果具有片面性,其仅仅表示与最优序列之间的关联性。为了更加客观地对比每一个状态所处的态势值,还需要了解该状态下与最差状态下的关联度,并借助于TOPSIS方法的思想[27],综合评判当前的态势值。基于此分析,本文方法采用优差序列进行对比,综合评判当前的状态。
(1)参考序列的确定
选取数据样本中每一个指标的最优序列和最差序列。
最优序列:
xbest=min(x0,x1,x2,…,xp)。
最差序列:
xworst=max(x0,x1,x2,…,xp)。
式中:p为待评价指标的数目;xbest代表各个指标的最优序列,当数据不是极小值为最优时,需要针对数据进行极小值变换;xworst代表各个指标的最差序列,同样需要做极大值变换。
(2)计算关联系数
在常规的灰色关联分析算法中,一般要根据式(9)先进行最大差值与最小差值的获取,再根据式(10)进行关联系数的计算。
(9)
(10)
式中:k=1,2,…,m,i=1,2,…,n;ρ为分辨率系数,0<ρ<1。若ρ越小,关联系数间差异越大,区分能力越强,通常ρ取0.5。
由于我们取的是每个指标的最优与最差值,因此在常规的灰色关联分析法中,可以省去式(9)的计算,使用改进后的式(11)进行计算。
(11)

(3)计算最终的关联系数
经过与最优最差序列的对比,我们得出了最优与最差序列下的关联系数。在最优序列下得到的关联系数代表与最优情况的距离,最差序列下的关联系数表示与最差情况下的距离。
在TOPSIS方法中,通过计算各评价对象与最优最劣向量的欧氏距离来评估每个向量的优劣,如果一个对象距最优向量越近的同时又远离最劣向量,毫无疑问为最好。因此借助于TOPSIS方法的思想并根据TOPSIS中采用的最优距离占比的公式,本文方法通过最优占比率来综合两种情况得出一个客观情况的关联系数:
式中:ξfin(k)表示第k个参考序列的最终关联系数。
(4)计算当前某一事件的客观评价值
与常规的灰色关联法相区别,抛弃原先的统一权值的方案,考虑到每个待评价指标的重要程度,本方法融合了经过改进的CRITIC方法得到的权重值,进行最终评价值加权[28]计算。
式中:Scorei表示第i个事件的最终评价值,Wj为根据改进的CRITIC方法中式(8)计算而来。
(5)计算时序内系统网络安全态势值。
(12)
式中:Score为最终的时序内的系统网络安全态势值,N为时序内的事件数目。
2 实验与分析
本节通过在公开数据集NSL-KDD与实际电网数据集进行实验,验证本文算法的可行性、有效性以及实际评估的准确性、实用性。由于所提算法序列选取的特殊性,因此要求样本中必须包含最优与最差情况下的状态序列,并且由于该算法是通过对优差序列的对比来实现对当前状态的评估,因此线性指标更有利于最终结果的准确评估。
2.1 实验1:算法有效性验证
2.1.1 数据集选取
实验采用NSL-KDD数据集中的部分数据,包括DoS、U2R、R2L、Probe、Normal五类网络数据,相应攻击信息如表1所示。

表1 攻击信息表
根据Staudemeyer[29]与数据集中字段选取了较为容易获取到的8个重要特征用于态势感知评估,分别为src_bytes(sc)、dst_bytes(db)、count、serror_rate(sr)、dst_host_srv_count(dhsc)、dst_host_diff_srv_rate(dhdsr)、dst_host_same_src_port_rate(dhsspr)、dst_host_rerror_rate(dhrr)。
2.1.2 评估设置
参照杨宏宇等[30]文章中的评价指标来对所提出的方法进行期望对比实验,并基于通用漏洞评分系统[31]制定攻击影响评价表,如表2所示。

表2 攻击影响评价表
计算网络安全态势值:
(13)
式中:M为期望网络安全态势值,p为攻击概率,Ii为第i次攻击所处的攻击类型的影响值,ni为第i攻击出现的次数,N为总样本数量,n为样本中表现为normal的样本。
根据《公共互联网网络安全突发事件应急预案》[32],将网络事件告警分为四个等级,分别为一般、较大、重大、特重大。因此针对网络安全态势,分为五个等级,见表3。

表3 网络安全态势评分表
2.1.3 实验参数设置
本文选取了8个有效的待评价指标,因此在变异系数设置中,本次实验设置α=0.5,β=0.125。
针对实验中分辨系数的选取,随机选取了9组实验样本分别进行了不同的取值实验,表4为分辨系数取0.01~0.7的结果。
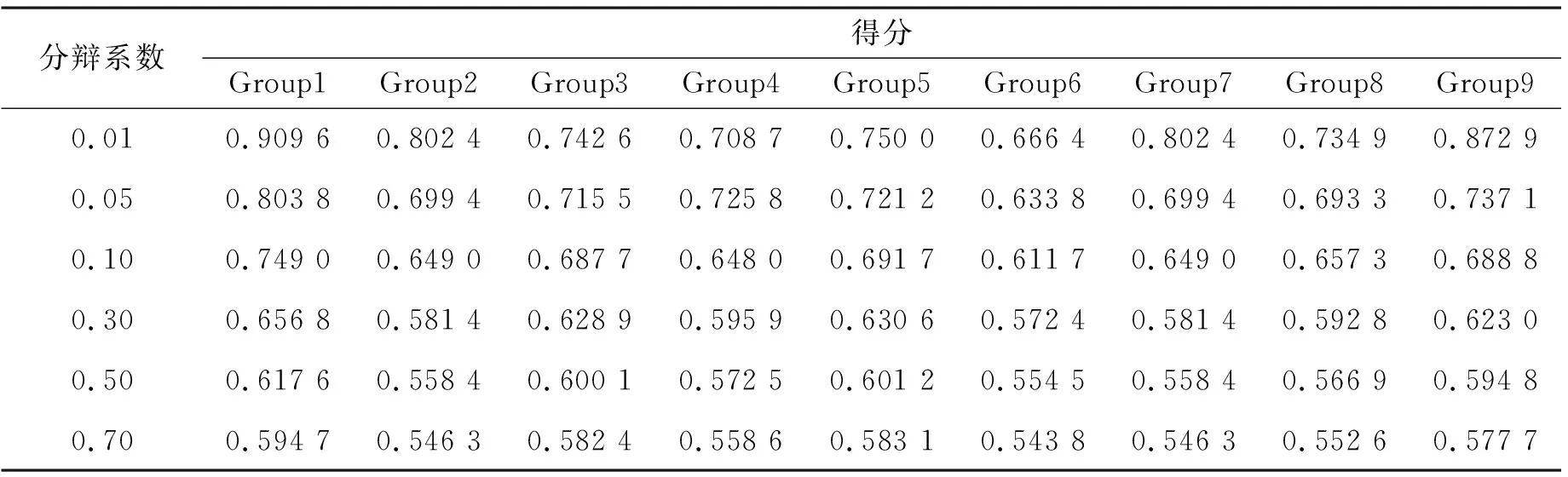
表4 不同分辨系数结果对比
根据表4中数据可得,每一组的结果可大致看作是随着分辨率系数的增大而增大,一般情况下分辨系数取0.5。由表4可以得出,在分辨率系数取到0.3~0.5的情况下,实验样本都聚集在[0.54,0.62]这一区间内,这与实验样本严重不符;当取0.01时,实验样本得分取值偏高,为了使最终的结果符合实验样本对整个网络的影响,综合测试结果与文献[33]本次实验的分辨率系数选取为0.05。
2.1.4 权重的改进结果
随机选取100组进行权重对比实验,其中有CRITIC算法、熵权法(EWM)、CRITIC与熵权法的常规结合,以及我们此次用于网络安全态势评估的基于变权的改进CRITIC法(VAR_CRITIC)。表5为不同方法对8个待评价指标的权重计算结果。
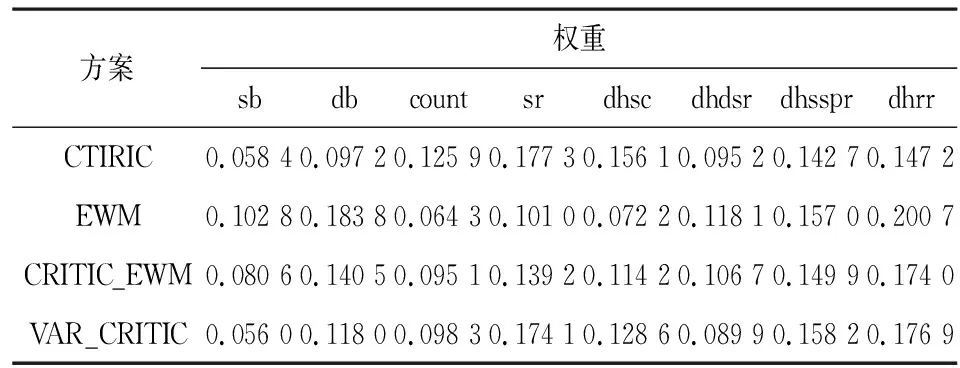
表5 权重结果
2.1.5 评估结果
在随机选取的100组样本中,对其所处的安全态势值进行了评估,并通过准确率指标来反应本文方案的可行性。准确率的定义:本文所选的方案评估得到的网络安全态势对应区间与实际的网络安全态势对应区间相对应的占比率:

由表6可以看出基于EWM算法的正确率最低,基于CRITIC方法具有较高的准确率,CRITIC与EWM的常规结合也表现出了较高的准确性,但是经过改进后的CRITIC与改进后的灰色关联分析法相结合后其准确率达到了97%,进一步说明了本文所提方法的可行性与准确性。
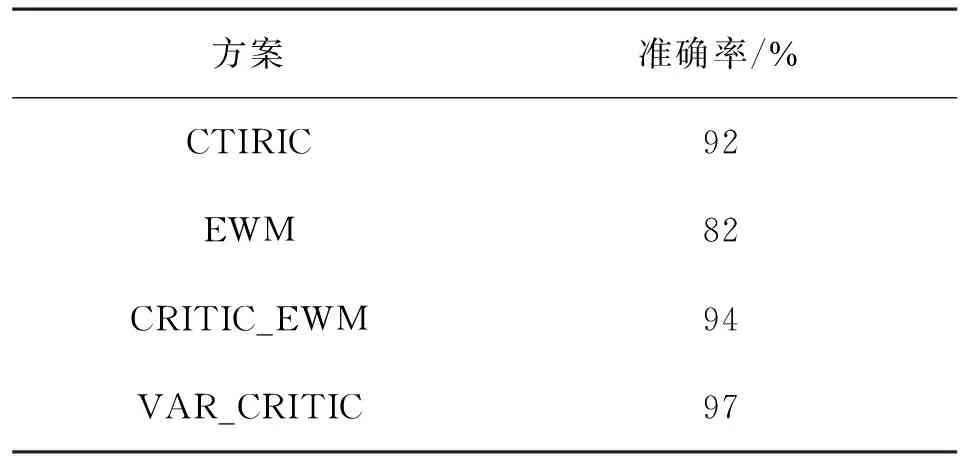
表6 准确率对比
最后通过随机选取10组不同的实验样本,利用不同的权重方案来计算最终的网络安全态势与期望态势相对比,其中期望态势由式(13)评估得到,并增加了与最差序列的相关性(Worst sequence correlation,WSC)作为参考,其结果见表7。

表7 基于数据集NSL-KDD评估结果
由于本文在灰色关联分析中采取了优差序列对比的方式来计算最终网络安全态势,因此在差序列相关性较大的情况下只有本文所阐述的方法在结果上与实际态势值最为接近,其他的方法都过高地估计了态势值。另外,从整体上来看,改进后的灰色关联法所得到的网络安全态势值与实际态势值最为接近,并且其数值都平稳的落在了与实际态势值相同的等级区间内,与实际情况相一致,进一步验证了所提方法的正确性。
2.2 实验2:算法实用性验证
为了验证该算法的实用性,我们收集了某地电网运行设备的部分流量数据,并从中提取了8个重要指标、10组时序内的事件进行试验评估,其中设置α=0.5,β=0.125,分辨率系数为0.05,评估结果如图1所示。

图1 基于电力数据评估结果
从图1电力安全态势评估结果来看,该电力系统整体均处于比较安全的状态,所选取的方法均具备一定的有效性,但在众多方法的评估结果中,其他方案因没有考虑到反向关联均过高地评估了当前态势值,本文所阐述的方法与期望态势值最为接近,基本能够准确表示出当前系统所处的网络安全态势值,证明了该方法在实际应用中的有效性与可实践性。
2.3 实验结果分析
通过对实验1与实验2中实验结果的对比分析,该算法在公开数据集NSL-KDD上的测试取得了较好的结果,其评估准确率较以往算法有了较大的提高;通过实验2抽取某地电网相关设备流量信息的8个相关指标对电网安全态势进行评估,并针对不同的算法进行了详细的对比实验,验证了该算法在实际应用中的可行性。
由第二部分针对该算法流程的分析可知,该算法并不是针对样本的训练学习来得出结果,而是通过最终优差序列的对比来评估当前状态,因此样本大小对实验结果并不会产生很大影响,但由于其最终结果均依赖于优差序列的选取,因此优差序列会严重影响实验结果的评估。
由于该算法不依赖于数据量,因此在与部分需要训练的算法的对比中更据有优势,特别是在数据量较小的场景中。该算法的提出是针对电网时序数据内进行实时动态网络安全状态评估,但由于该算法的普适性,使得其不仅适用于多指标网络安全态势评估,并且适用于其他领域的状态评估,例如教师业绩评估、地域适宜居住指数评估、设备健康度监控等。
3 结束语
针对传统灰色关联分析法在处理网络安全态势中没有考虑指标关联性与量化标准有残缺的问题,本文提出了一种基于变异系数的改进CRITIC法与量化灰色关联分析法的结合算法。该方法首先通过加入激活熵与变异系数到CRITIC中得到各个指标的权重,然后根据得到的权重加入到改进后的优差序列对比关联分析算法中,计算得到网络安全态势量化值。实验结果表明,笔者所提出的算法在网络安全态势评估中相较于其他的算法具有更高的准确性以及有效性,其所评估得到的态势值最接近实际态势值,能够较为准确地评估当前系统所处的状态。
在下一步工作中将尝试针对大规模数据进行态势评估并进一步优化灰色关联算法,提升计算效率。

