三角形三内角的半角正弦的一个下界
——兼有奖解题擂台(139)的解答
2022-04-26 13:30:32四川成都实验外国语学校宿晓阳邮编611130
中学数学教学 2022年2期
四川成都实验外国语学校 宿晓阳 (邮编:611130)
问题在△ABC中,设其外接圆半径及三个旁切圆半径分别为R、ra、rb、rc,求证:sin
证明设△ABC的三边为a、b、c,其外接圆和内切圆的半径为R和r,半周长和面积为s和△,则由三角形中熟知的恒等式

据对称性不妨设a≥b≥c,则易知
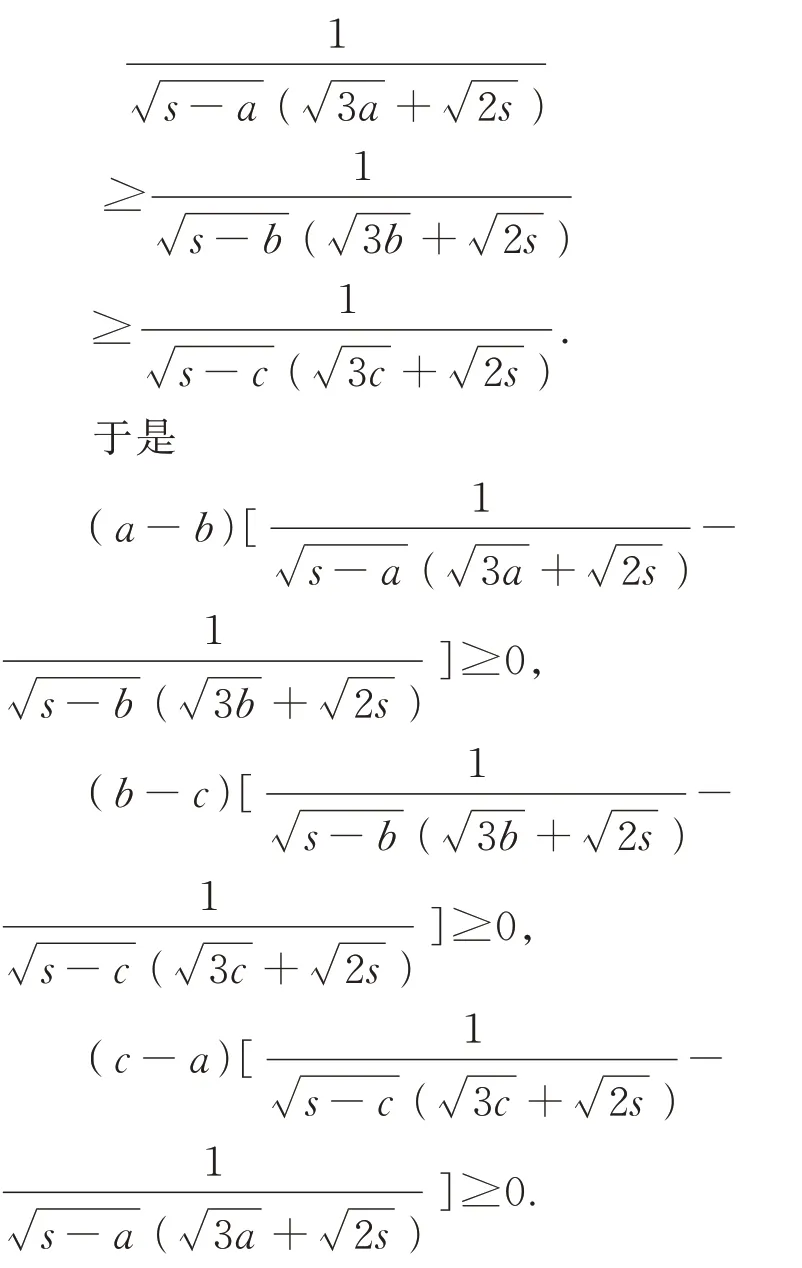
上述三式相加,即得不等式①成立.故证式成立.
评注(评注人 郭要红,评注时间 2022 年3月29 日)本擂题收到正确攻擂稿件3 篇,按时间顺序,作者依次为林国红(广东佛山市乐从中学,邮 编 528315,收 稿 时 间 2022 年2 月20 日12:13),宿晓阳(四川成都实验外国语学校,611130,2022 年2 月24 日10:37),严复卓(甘肃省武威市第十八中学,733000,2022 年3 月14 日20:03).宿晓阳老师的证明简洁清楚,故选择他的来稿作为擂题的解答,林国红老师是本擂题的获奖人.
猜你喜欢
中等数学(2021年2期)2021-07-22 06:21:52
中等数学(2020年9期)2020-11-26 08:07:28
中学数学教学(2019年3期)2019-06-21 08:10:52
长江丛刊(2018年24期)2018-11-14 15:58:43
中等数学(2018年8期)2018-11-10 05:07:22
中等数学(2018年7期)2018-11-10 03:29:04
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
人大建设(2017年12期)2017-03-20 05:22:10
韩国语教学与研究(2017年2期)2017-03-07 17:48:24
校园英语·中旬(2016年7期)2016-05-14 07:08:56

