基于卡尔曼滤波算法的刀具磨损状态预测*

王 全，靳伍银

(兰州理工大学机电工程学院，兰州 730050)

0 引言

在机加工过程中，刀具的磨损程度影响着机加工产品的质量，因此对于刀具磨损的研究得到了广泛的关注。而在常规的加工过程中，刀具磨损的判断方法通常以加工时产生的噪声与已加工工件的表面质量作为判断依据，但是这些方法对工人师傅的经验要求很高，并且在噪声严重的环境中并不能及时发现已经处于磨损状态的刀具。

刀具的磨损形式通常分为三种形式：前刀面磨损，后刀面磨损与前后刀面同时磨损[1]。正常情况下刀具磨损是一个逐步变化的过程，随着加工次数的增加，加工时长的增加，刀具的磨损也随着其不断地增加，刀具处于新刀的时候，由于可能的不确定因素，新刀刃会出现一系列的表面缺陷[2]，在早期切削的过程中,其刀刃会快速进入一个相对平稳的阶段，并且保持较小的磨损速度。

随着加工过程的进行，刀刃的磨损不可避免地发生，随着几何尺寸的改变，会导致工件表面质量下降[3]与尺寸误差变大[4],这些原因都会导致不合格件数量的增加，对工厂的经济效益产生影响。根据大量的数据统计与研究证明[5-6]，对机床的刀具磨损进行监测后，由于人工与技术方面所导致的故障停机时间减少了75%，生产率在原有的基础上提升了10%～60%，机床的有效工作时间较之以往提高了50%。

对于刀具磨损的状态识别主要分为直接监测法与间接监测法[7]，直接监测法顾名思义，直接对刀具进行观察与测量并获取相关的信息，常用的方法有利用高倍显微镜对刀具进行观察即光学测量法，该种方法通过对刀具表面几何形状的变化量与判断刀具磨损的标准进行直接对比从而确定磨损情况[8-9]。间接监测法是通过采集与刀具磨损有关的信号，通常采用的信号有切削力信号、振动信号、电流信号和声发射信号等[10-13]，然后将收集得来的信号进行时频域或希尔伯特黄变换处理[14]提取出刀具磨损相关的特征，最后结合人工神经网络与机器学习算法等技术得到对刀具磨损的状态预测。

为了对下一个加工过程的刀具磨损状态进行预测，本文利用卡尔曼滤波算法模拟出基于当前加工过程的下一个加工过程的周期铣削力，并利用随机森林算法对模拟出的铣削力所提取的特征值进行分类，间接的达到预测刀具磨损状态的目的。

1 数据集的特征处理与划分

实验数据来源于PHM society刀具磨损预测数据比赛。原始实验数据主要包括三相铣削力信号、三相振动信号与声发射信号，其中C1、C4与C6数据集中含有刀具磨损量测量数据，刀具磨损量的变化趋势如图1所示。C4与C6数据集中刀具磨损量变化趋势相对明显，而C1数据集的磨损量变化趋势相对缓和，在划分数据集标签时难以界定其分类标签。

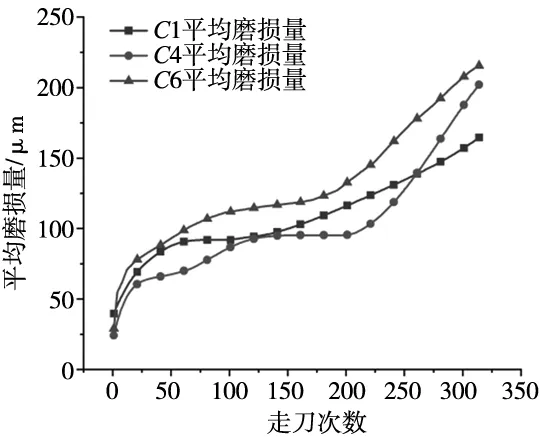
图1 平均磨损量

在本次分析过程中，对实验数据进行上四分位截断法，具体步骤为：①将原始信号做一次绝对值处理；②求出①中的上四分位值K；③分别从数据的首尾开始判断，取第一个不小于K值的信号数据位置并将其截断。

通过对切削力信号的分析比较发现，相比较于刀具磨损量的大小，铣削力信号的变化趋势更加具有一致性，并且在加工过程中无法做到实时停机对磨损量进行测量，所利用间接监测方法更加符合实际生产加工情况。例如以三相峰值铣削力与刀具磨损量进行比较，其结果如图2所示。其中X方向的力相比较于其他两个方向的力的趋势更加一致，故在后续的数据处理过程中均以X方向的铣削力数据作为输入数据。

图2 趋势对比图

对于机器学习算法来说，想要获得较高的识别准确率，需要对数据进行进一步的处理，通常的做法是对数据进行时频域处理[15]。对于频域抽取的特征值为利用快速傅里叶变换所求得的频率重心。

利用小波包分解分解算法[16]，可以将原始力信号分解至不同的频段并且重构，这些被分解的信号都带有一定的能量，通过分析发现，使用DB5小波的小波包6层分解的前三层的能量占比拥有较为直观的趋势，其能量占比在整个数据集的走势如图3所示。也为了减少在数据分析过程中的计算量，对特征数据使用PCA主成分分析法对数据进行降维，所以最终的刀具磨损铣削力信号的特征值选择如表1所示。

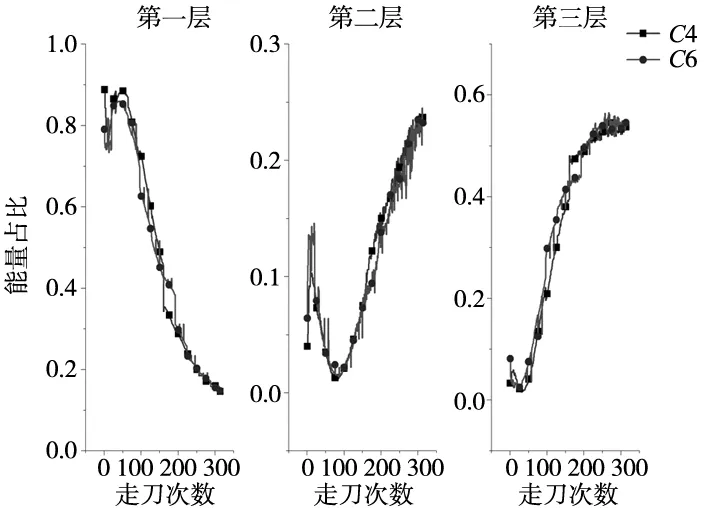
图3 X方向力小波包分解的能量占比

表1 特征值选择

根据上述内容，最后使用K-means聚类算法对完整的走刀过程划分为5个阶段，最后一个阶段定义为刀具磨损阶段，其整个数据集划分如表2所示。

表2数据集划分

2 模型与算法

2.1 卡尔曼滤波算法

刀具磨损是一种不可逆的逐渐退化过程，下一次加工时刀具所处的状态是由本次加工结束后的状态所决定的，其过程符合一阶马尔科夫过程[17]，所以可以使用状态方程对其退化过程进行描述：

xk=fk(xk-1,wk-1)

(1)

式中，fk为非线性函数；Wk为已知状态的噪声；xk为系统当前所处状态。

并且铣削力的变化也是一个动态过程，但是其变化过程是一个有规律的周期过程，其变化过程如图4所示，假定在加工过程中工件的质地均匀，故铣削力的变化只与刀具切削刃与工件待加工面的接触有关，所以铣刀的每一次完整转动过程也可以理解为一个由左至右的单向的离散时间序列的过程，同样符合一阶马尔科夫过程，可以利用卡尔曼滤波算法对其铣削力的变化趋势进行预测。

图4 三项铣削力

经典卡尔曼滤波算法主要由预测过程与校正过程所构成[18]，在预测过程中状态方程由式(1)改写为：

(2)

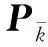
(3)

在校正过程中主要由这三个阶段构成：卡尔曼增益阶段、状态更新阶段与误差矩阵更新阶段。

(1)卡尔曼增益阶段，主要用于为预测与观测的两个协方差矩阵分配权重，其公式表示为：

(4)

式中，Hk表示为观测矩阵，由于本次数据集中加工参数不变，故在计算过程中其以单位矩阵代替；R为在观测过程中的一些无法确定的干扰噪声。

(2)系统状态更新阶段，主要利用卡尔曼增益阶段中所求出的Kk对系统当前的状态量进行更新：

(5)

式中，Zk表示在K时刻的观测值即传感器所收集到的数据。

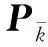
(6)

利用卡尔曼滤波预测的铣削力如图5所示。从图中可看出基于卡尔曼滤波算法所得出的预测值与真实值相比，其状态基本吻合，可以用作对于下一次走刀过程中铣削力的预测。

图5 基于卡尔曼滤波的铣削力预测

图6为将预测出的铣削力提取出的特征值进行归一化后与真实特征值的对比图。从图中可以看出只有小波能量占比的预测值与真实值之间有着些许差异，而其他特征的趋势基本吻合。由于多特征提取可以避免在此种情况下在后续状态识别中准确性差的问题，故通过卡尔曼滤波算法得到的周期铣削力的特征提取值可以用作对于下一次走刀过程中的周期铣削力的分类预测。

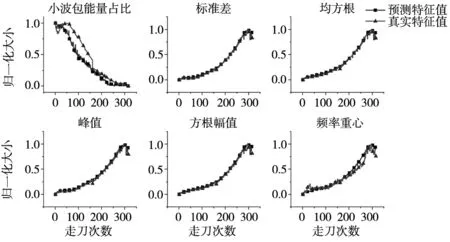
图6 预测特征值与真实特征值对比

2.2 随机森林分类算法

随机森林算法是一种集成思想的分类算法[19]，通过将多个决策树组合，形成累积效果，利用多数投票机制完成对于数据的分类。其优点在于学习速度快，可以处理高维数据，并且有着较高的准确性。

其特征选择指标通常由信息增益(ID3)、增益率(C4.5)、基尼系数(Gini)和卡方检验来决定[20]，由于本文决策树在构建过程中的特征选择是基于基尼系数，故在本文的随机森林算法中也使用基尼系数作为特征选择指标，其计算公式如下。

第二，自然计算表现出一种句法形式，但并不是严格意义上的句法。提出这个假设至少有两个原因。首先，在自然科学中使用计算模型的主要原因是为了从科学解释中消除“机器中的鬼魂”。如果通过纯粹的机械过程我们能够解释一些行为或认知能力，那么我们有信心不陷入循环论证(例如，“小人论”，在认知主体脑中存在一个掌控其认知活动的“小人”，而这个“小人”极有可能被其“脑”中的“小人”掌控，如此无须循环)，并把我们试图解释的事情看作理所当然。第二，为了设计自主的智能机器，我们必须要能够将自然计算简化到纯机械过程，即简化到我们可以设计和构建的系统中，否则无法参与应用的自然计算是没有意义的。

(7)

式中，pi为每个特征值对相对于分类结果的概率值。基尼系数越大则证明数据划分结果的不确定性越大，反之则证明数据划分的结果准确。

决策树作为构建随机森林模型的基本组成部分，其通常是通过构建二叉树从而达到分类的效果，每一个特征即为节点，在进行分类时选择可能性都会对半，迅速缩小选择范围。故式(7)即可写成如下形式：

Gini(p)=2p(1-p)

(8)

对于每一个特征来说，均可以将数据划分为不同的类，例如令某一可以将数据划分的特征F作为数据集的分割点，D1为符合特征F的子集，D2为不符合的子集，所以对于数据集D与特征F的基尼系数的计算公式写为：

(9)

式中，Gini(Di)表示为该子集的基尼系数；|Di|表示其子集中剩余节点的个数。

通过如上公式可以计算出单个决策树所划分的结果，最后利用多数投票机制即可完成对于数据的分类如图7所示，是将C6数据集作为训练样本对C4数据集的测试，其准确率为99.04%。

图7 预测结果

图8为单个决策树在不同分割深度情况下对于数据集的划分情况，其数据是为C4特征值中的随机两组数据用于可视化。可以看出，随着决策树深度的增加，数据集的划分越来越准确。

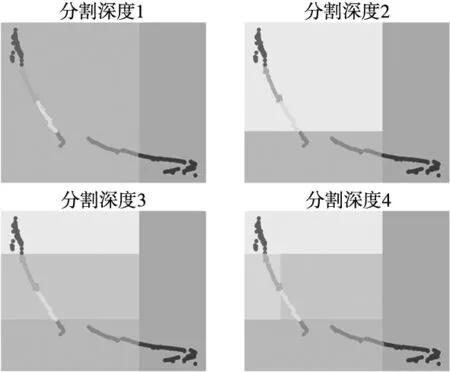
图8 决策树分割数据过程

3 对于刀具磨损状态模型的训练与预测

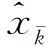
其具体的计算过程如下：

(2)读取C4数据集的x方向铣削力数据作为观测值，同时在C6数据集中读取相应的数据作为估计值；

(3)根据卡尔曼滤波算法，利用(2)中的观测值与估计值计算出预测值；

(4)将(3)进行多次循环迭代后获得的铣削力作为预测值；

(5)将(4)中的预测值提取特征，利用(1)中模型对预测值进行状态识别后返回(2)。

图9为利用上述计算过程后，与实际标签相比较的结果。

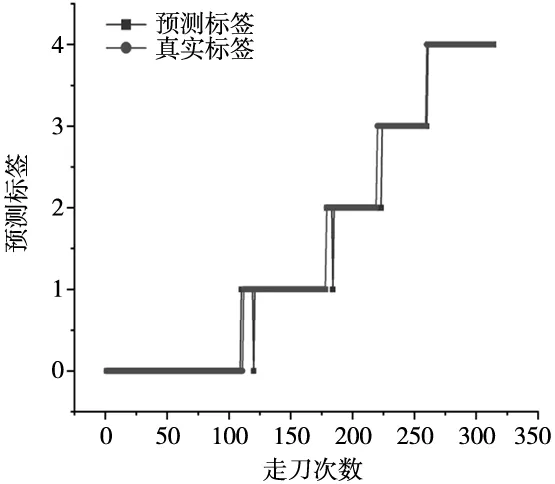
图9 标签值对比

可以看出，其准确率为98.73%。可以在刀具实际进入磨损阶段前预测出下次加工过程是否会进入磨损阶段。

4 结论

将铣削过程看作为一个动态变化过程，通过卡尔曼滤波算法由上一过程的数据预测出下一次加工过程的完整数据，使用随机森林算法可以在下一次加工前有效的判断该次加工刀具是否会在下次加工过程中进入磨损阶段。模型的训练以及结果表明，本文所提出的组合模型能够有效地对下一次的加工过程进行预测与识别，且所需的计算量小，但是均建立在单一工况条件下，下一步的研究中将通过采集不同工况下的各个阶段的刀具磨损数据，以建立一个初步的多工况下的刀具磨损预测模型。