优化改进A*和动态窗口法的机器人路径规划*

辛 鹏，马希青

(河北工程大学机械与装备工程学院，邯郸 056038)

0 引言

移动机器人具备自主移动、运动灵活等特点，在工业生产以及家政服务等领域有广泛的应用和开发前景。移动机器人开发的核心部分是机器人路径规划，即针对当前环境规划出从起始位姿到目标位姿的安全无碰撞路径[1-3]。高效的路径规划算法能使移动机器人迅速规划出最优路径。目前较为常用的算法有以下几种：快速搜索随机树[4]、A*算法[5]、动态窗口法[6]、蚁群算法[7]、粒子群算法[8]等。

A*算法是经典的启发式路径规划算法，但算法存在规划的路径拐点和冗余路段较多等诸多问题。目前，针对A*算法已经做了较多研究和改进。槐创锋等[9]提出将A*算法领域扩展为7×7与优化评价函数后的动态窗口法相结合的融合算法，但在搜索过程中需判定父节点与子节点的连线中是否经过障碍物，路径搜索效率在复杂环境中会降低。孔继利等[10]对路径进行双向搜索，优化了评价函数，并将文中的改进算法与Dijkstra算法和蚁群算法进行比对，验证算法高效性。陈娇等[11]通过提取关键节点剔除冗余子节点，并按照相邻节点分段使用动态窗口法规划路径，但是未能有效减少A*算法搜索时间。王中玉等[12]改进了代价函数权重，并引入了一种障碍物扩展策略，使路径更加合理。张志文等[13]利用JPS算法跳跃扩展子节点，缩短搜索时间，并对文中改进A*算法规划的路径使用贝塞尔曲线进行平滑处理。

针对A*算法搜索效率不高，规划路径较长且不利于机器人行驶，将优化改进A*算法规划的路径按照节点分段使用动态窗口法。在全局规划方面，扩大搜索邻域，调节代价函数，剔除冗余子节点、减少路径长度，提高搜索效率。在局部规划方面，将优化后路径分段使用改进动态窗口法，避免陷入全局最优，提高机器人移动安全性。

1 优化改进A*算法

A*算法在搜索过程中利用目前所知的状态信息生成全局路径。传统A*算法思想是引入代价函数判定静态环境下当前节点代价值，在开放列表中找到代价最小值进行扩展直到目标节点也在开放列表中，完成搜索。但A*算法搜索速度较慢，路径拐点较多，针对这些问题从以下3个方面进行改进。

1.1 改进代价函数

传统A*算法的代价函数如式(1)所示。

f(n)=g(n)+h(n)

(1)

式中，g(n)为起始节点到当前节点的代价值，使用起始节点到目标节点欧几里得距离表示；h(n)是当前节点到目标节点的代价值。考虑到实际环境中障碍物较多，机器人在多数情况下并不能从当前节点直线到达目标点，且使用欧几里得距离会增加计算量降低路径规划效率，因此采用曼哈顿距离表示，如式(2)所示。

h(n)=|xg-xn|+|yg-yn|

(2)

式中，(xn,yn)为当前节点坐标；(xg,yg)为目标节点坐标。

针对传统A*算法搜索路径时间较长的问题，优化代价函数，增大前期h(n)值，提高搜索效率，使得规划路径更快向目标节点靠近。改进代价函数为式(3)。其中R为初始节点到目标节点的欧氏距离。

(3)

1.2 扩展搜索邻域

传统A*算法搜索邻域过小导致规划的路径中拐点以及路径节点较多，不利于机器人的移动和控制。为此，应适当扩大搜索邻域去除多余子节点。当扩大搜索邻域时，需判定父节点与子节点的连线是否会经过障碍物，若搜索邻域扩展过大，算法在复杂环境搜索路径时会增加计算量导致搜索效率较低，因此采用扩充为5×5搜索领域。如图1所示，左侧为A*算法的搜索邻域，右侧为改进A*算法的搜索邻域。

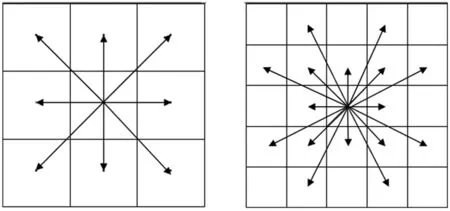
(a) A*算法的搜索邻域 (b) 改进A*算法的搜索邻域图1 传统A*算法与改进A*算法搜索邻域对比

1.3 路径优化

改进算法规划的路径中存在大量冗余路段，应采用一种关键点提取的算法，提取出路径关键转折点，剔除冗余路段，重新规划路径。重新规划后的路径长度更短，拐点更少，具体实现如下：

(1)首先得到规划路径中的所有节点{x1,x2,…,xn}，x1为起始节点；xn为目标节点；V为关键点集合。

(2)以x1为出发点，依次直线连接x2,x3…直到当与xm的连线中存在障碍物，则将xm-1加入V。x1～xm-1之间的节点都为冗余节点，此时将xm-1设置为出发点，依次直线连接xm,xm+1…直到存在出发点与目标点直线连接。

(3)目标节点加入到V，依次直线连接V中所有节点完成优化，优化步骤如图2所示。

(a) 改进A*算法 (b) 提取关键转折点 (c) 优化后路径图2 优化步骤

优化后，路径长度从39.253 6减少到了36.980 5，优化了5.79%，节点从25个减少到10个，优化了60%。路径拐点从17个减少到8个，优化了52.94%。优化后的路径仍存在移动机器人易与障碍物发生碰撞且不能动态避障，路径不够平滑等问题。

2 改进动态窗口法

动态窗口法主要是在速度空间中提取多组速度，模拟出提取速度下一段时间内机器人运行轨迹，评价所有提取到的轨迹并选取最优作为当前轨迹。评价函数中加权比例固定，不利于机器人快速向目标点靠近，将传统加权系数改进为动态加权系数，实现动态调整，提高搜索效率。

2.1 机器人运动学模型

现假设机器人运动过程中在Δt时间内是沿直线运动且机器人全向运动，速度为v；角速度为ω。此时机器人的运动轨迹可根据式(4)得到：

(4)

届时根据速度分辨率在速度空间中采集多组速度，得出移动机器人相应运动轨迹。

2.2 速度采样

在速度空间中存在多组数据，但考虑到机器人组成结构以及运行环境，限制采样速度。机器人自身速度限制如式(5)所示。

Vm={(v,ω)|v∈[vmin,vmax],ω∈[ωmin,ωmax]}

(5)

机器人在运动过程中由于电机力矩有限而存在速度约束，因此机器人运动中实际运动速度为：

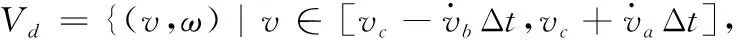
(6)

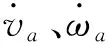
为保证机器人的安全应使机器人碰撞到障碍物之前停止，因此需要对其速度进行限制：

(7)

式中，dist(v,ω)为当前速度对应轨迹中距离障碍物最小的值。

2.3 改进评价函数

在所采样的速度中有多组可行轨迹，此时需要评价选取最优路径即使用评价函数。在局部路径规划中，此时评价函数为:

G(v,ω)=σ(αhead(v,ω)+βdist(v,ω)+γvel(v,ω))

(8)

式中，head(v,ω)是用来评估在当前速度下，目标方向与模拟出的轨迹末端方向偏差；vel(v,ω)是对机器人当前运转速度大小的评价；σ为平滑函数；α、β、γ为加权系数。

式(8)中α与γ比例值固定，不利于机器人快速向目标点靠近。对加权系数做出调整，当移动机器人距离障碍物较远时，使机器人方向占比更高，向目标点方向靠近，当机器人靠近障碍物时，提高移动速度占比，快速绕过障碍物。根据移动机器人与障碍物的距离动态调节系数。改进评价函数如式(9)所示。

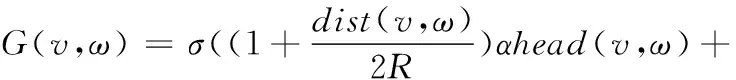
(9)

式中，R表示障碍物半径，在计算中将dist(v,ω)设定一个最大值2R，如果不设定，当路径中没有障碍物时将占比过重，因此dist(v,ω)∈(0,2R)。

传统动态窗口法如图3所示，改进动态窗口法路径如图4所示，两种方法对比如表1所示。

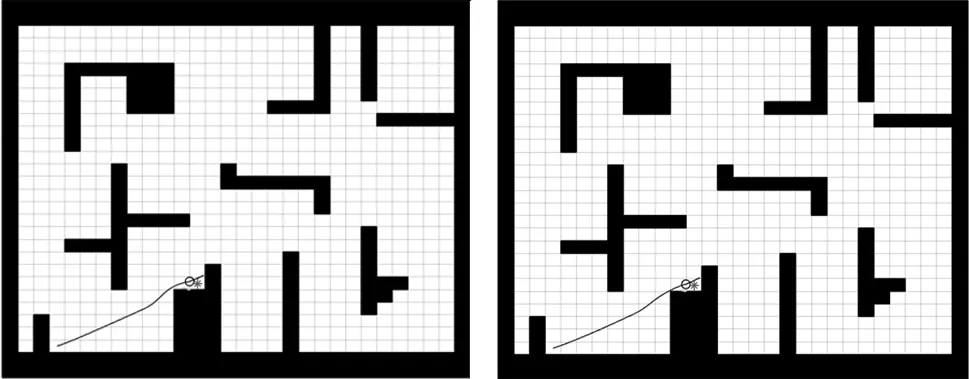
图3 传统动态窗口法 图4 改进动态窗口法路径

表1 传统动态窗口法与改进动态窗口法时间对比

通过对比路径，两种算法路径基本保持一致。通过对比规划时间，改进算法时间减少了13.41%，改进评价函数有效地减少了搜索时间，提高搜索效率。

3 融合算法

传统的动态窗口法参照点只有目标点，因此寻找路径中容易出现局部最优，致使找不到全局路径。改进的A*算法优化路径后依然存在路径不够平滑，机器人移动过程中存在安全隐患等情况。

针对这两个问题，将优化后的路径按相邻节点分段。在每段中使用改进动态窗口法。以相邻节点构成向量的角度作为机器人每段移动的初始角度，增加搜索效率。将路径分段使用改进动态窗口法时，分段路径中没有过多障碍物，以相邻节点为目标点，可以较为快速的找到路径，实现局部最优。

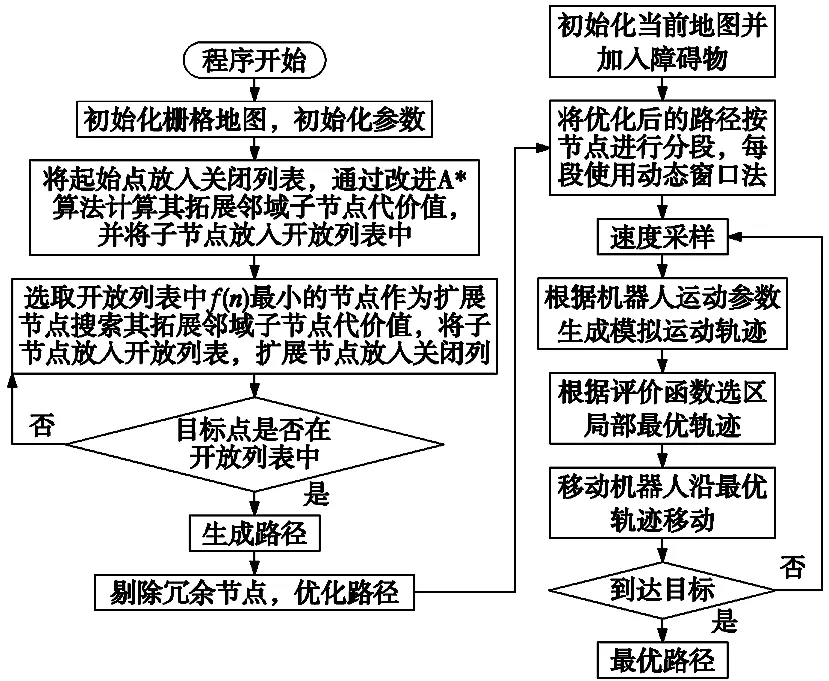
图5 融合算法实现流程图

4 仿真与分析

在MATLAB中构建栅格地图验证算法可行性。使用经典的二维栅格地图表示机器人行驶时的周围环境，黑色栅格表示障碍物，空白栅格表示可通行区域。起始点(23,28)，目标点(2,3)。分两组实验对融合算法进行验证。

实验1：验证优化改进A*算法的效率以及融合算法的实现。如图6～图9所示。4种算法性能对比如表2所示。

图6 传统A*算法路径 图7 优化改进A*算法路径

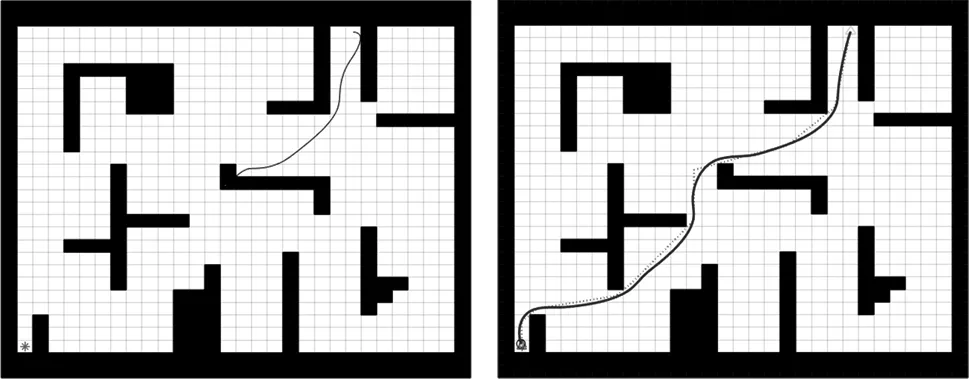
图8 传统动态窗口法路径 图9 融合算法路径

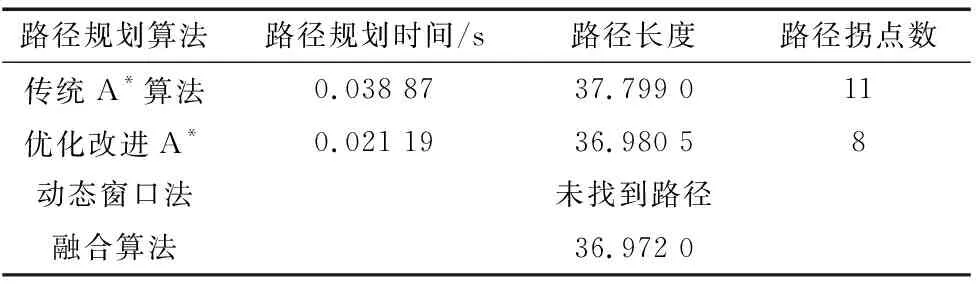
表2 4种算法对比

如表2所示，相较于传统A*算法，优化改进A*算法路径缩短了2.17%，路径规划时间减少了45.48%，路径中拐点减少了27.3%。相较于传统动态窗口法陷入局部最优未能找到路径，融合算法成功找到路径并且路径长度比优化改进A*算法规划的路径更短。

实验2：在优化改进A*算法生成的路径中加入障碍物用于验证本文算法动态避障性。红色小块为加入的障碍物，如图10所示。

在路径中加入动态障碍物后，移动机器人的路径避开障碍物如图11～图13所示，机器人在运行过程中的线速度、角速度和机器人姿态变化分别如图14～图16所示。

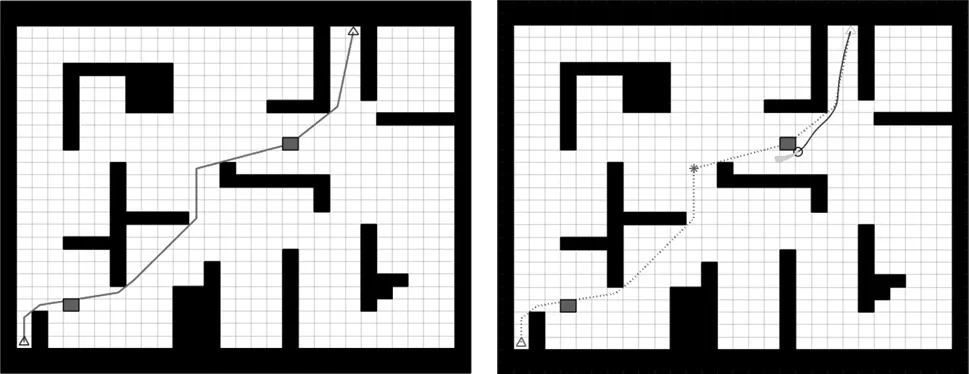
图10 在优化改进A*算法路径中加入障碍物 图11 移动机器人避开第一个障碍物

图12 移动机器人避开第二个障碍物 图13 机器人整体运行轨迹

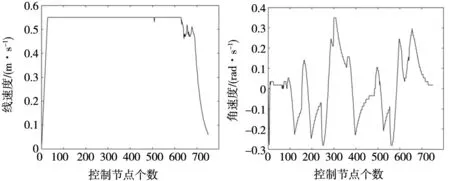
图14 机器人运行线速度 图15 机器人运行角速度

在优化路径中加入障碍物后，移动机器人依然可从起始点到达目标点且成功避开了障碍物，达到了动态避障的目的。

5 结论

为使机器人路径规划实现全局最优以及在复杂环境中动态避障，本文将优化改进A*算法按照关键节点分段使用改进动态窗口法进行路径规划。由仿真结果得，相较于A*算法，优化改进A*算法规划的路径更短，路径节点更少，规划效率更高。融合算法不会陷入全局最优，且路径更短。在原有规划路径中加入障碍物，机器人能够成功避开，达到了动态避障的目的。