基于地铁运营日志文本挖掘的危险源辨识算法研究*
牟庆泉,丁小兵,刘志钢,吴先源
(上海工程技术大学 城市轨道交通学院,上海 200336)
0 引言
目前,国内外大型城市内部交通堵塞、环境污染、土地资源紧张等问题已为常态,而以地铁为主的城市轨道交通凭借其高运能、低能耗、安全度高等优点,在各类大型城市中广泛运行。截至2020年12月31日,全国开通运营城市轨道交通的城市共44个,运营线路共233条,线路长度7 545.5 km,车站4 660座,共开行列车2 528万列次,累计客运量175.9亿人次[1],可有效解决大型城市交通面临的多种问题,同时带来巨大的社会效益。同时,各类险性事件的发生对乘客的人身安全以及运营企业的财产安全造成严重威胁。
为解决以上问题,国内外学者开展大量研究[2]。近年来,自然语言处理技术趋向成熟,并在多个领域广泛应用[3-5]。罗文慧等[6]对道路交通事故报告进行文本预处理,建立双隐层适应卷积神经网络,并通过样本进行训练,实现对安全风险源的辨识;李珏等[7]对建筑施工高处坠落事故报告进行特征提取,得到致因特征项、致因网络及致因集合,利用词云和网络结构图对结果进行展示;Li等[8]对美国天然气管道事故报告数据进行建模,通过文本挖掘提取有效信息,探究天然气管道事故严重程度和影响因素之间的时空相关性模式;Nasri等[9]运用文本挖掘中的情感和模糊词方法挖掘视频平台中评论的安全风险问题,证实该方法可被制造商和消费产品安全组织用来从在线视频中有效识别产品安全问题;Fa等[10]基于煤矿事故报告,采用文本挖掘技术建立煤矿人因分析分类系统,从多个角度识别人机交互系统框架中的层次结构关系;Xu等[11]利用文本挖掘技术设计翻译管理框架,并提出信息熵加权的术语频率,用于术语重要性评价,最终提取出影响建筑安全的核心因素。
现有研究针对行业事故报告,运用文本挖掘技术有效实现对风险或风险致因的挖掘和分析。但针对轨道交通领域,文本挖掘技术的应用研究较少,本文提出AFP-tree(Ameliorate Frequent Pattern-tree)算法,深度挖掘城市轨道交通运营日志中危险源与险性事件之间的强关联规则,最后得到地铁交通系统运营过程中的关键危险源集合,研究结果可为地铁运营单位实现“事前”风险预防提供方向和依据。
1 地铁运营日志数据预处理
运营日志作为地铁运营过程中的关键数据,包括地铁运营过程中所遇到的各种故障、突发事件、事件发生时间地点等多维度的信息记录。这些信息通常是对事件的一段描述,不能直接作为数据挖掘的对象,需要进行数据预处理,将其转化为适合算法分析的数据格式。
1)数据预处理流程
首先,地铁运营日志的原始数据中包含大量的正常调度、定期检查等信息,但上述信息与地铁运营险性事件不相关,将其定义为干扰数据,并做删除操作;对去干扰后的数据进行分词,在分词之前需要加载自定义专业术语词典,以提高分词准确率;最后进行去停用词操作,以提高危险源辨识的准确性。具体流程如图1所示。
2)干扰数据清理
选取上海地铁轨道交通的运营日志作为原始数据,共m条,首先使用Python语言对该部分数据进行去干扰操作,最后剩余n条有效数据,删除干扰数据的伪代码如图2所示。
3)Jieba分词及去停用词处理
本文借助Pycharm开发平台,分词使用Python中的Jieba库进行。Jieba库内置3种分词办法,本文选取更适合做文本分析的精确模式[12]。在对数据分词前加载自定义专业术语词典,用来提高分词的准确性,为保障文本处理质量,共构建643个地铁轨道交通危险源词汇与326个地铁轨道交通专业术语;分词完成后进行去停用词操作,删除日志文本中与研究不相关的词汇,以哈工大停用词表为依据,结合地铁运营特点,形成自定义停用词表,共包含1 894个停用词。具体处理结果见表1。

表1 Jieba分词与去停用词操作列举Table 1 Lists of Jieba words segmentation and stop words removal operation
经过文本预处理,将地铁运营日志转化为可用于进行文本挖掘的格式,即可以输入AFP-tree算法中进行定量分析。
2 基于AFP-tree算法运营危险源辨识
经典的Apriori关联规则算法缺点明显,学者通过改进提出FP-growth算法[13],但FP-growth算法需要重复访问树节点,在数据量较大时算法效率依然不能满足需求,本文借鉴FP-growth算法处理思想,并对其算法效率进行改进,提出AFP-tree算法,据此算法进行数据分析。
2.1 数据格式转换
假设在日志文件预处理后,每条数据中的单词个数为n,则其中连续2条数据表示如式(1)所示:
(1)
式中:Xi表示第i条数据,i∈(1,m);xj表示第j个单词的嵌入,j∈(1,n),对于相同的单词,用同1个xj表示。以此类推,可以将全部的单词以xj的形式进行表示。
基于列车运营时的调度日志数据,阐述利用FP-growth算法对原始日志数据进行处理,并深入挖掘关联规则的过程。首先,将获取的日志运用前述方法和步骤进行数据预处理,产生日志数据的存储形式,见表2。表中ID表示每条日志数据的编码,xj表示第j个单词的嵌入。将数据转化为可以用FP-growth算法处理的格式后,需要构建1个FP树,用以存储数据。

表2 运营日志预处理后的事件描述形式Table 2 Event description forms after preprocessing of operation log
2.2 FP树的构建及算法的改进
本文在计算过程中使用支持度和置信度2项指标作为数据处理过程中的判定依据,其中支持度用于计算数据关联出现的概率,置信度用以挖掘文本中的强关联规则,如式(2)~(3)所示:
(2)
(3)
式中:X,Y分别代表不同数据元素;P(XY)表示X和Y同时发生的概率;mXY表示X和Y同时发生的频数;Mall表示总数据量;P(X|Y)表示Y发生的条件下X发生的概率;P(Y)表示元素Y发生的概率。
构建FP树作为FP-growth算法的第1步,要先扫描全部数据,对所有元素项的频数进行累加计数,然后根据设定的支持度,过滤掉不满足支持度的数据,再对满足的数据由高到低进行排序,生成频繁项集事件元素表,设定支持度计数为2,所以在表3中重新排序后的x16、x17、x18等数据均被删除,如表3所示。

表3 频繁项集事件元素表Table 3 Event element table of frequent itemsets
FP-growth算法需要构建头指针表,用以存储全部元素项的出现频数,该指针指向树中对应元素项的首位节点,本文使用Python程序中的“字典”储存头指针表。最终构建结果如图3所示。
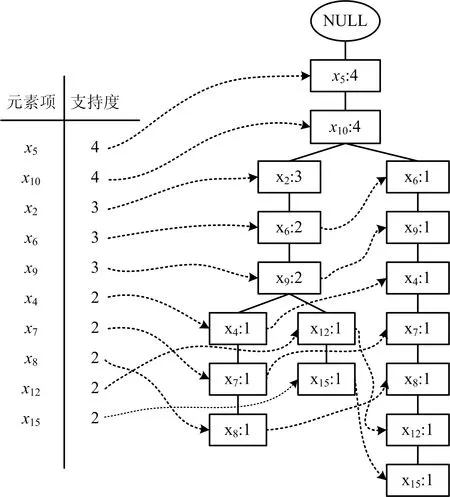
图3 构建FP树Fig.3 Establishment of FP-tree
在构建FP树后,要从FP树中挖掘频繁模式,由于FP-growth算法在产生条件模式基时,需要多次遍历公共路径,将占用大量计算机内存,同时使计算时间显著延长[14-15]。为提高算法效率,降低算法复杂度,对FP-growth算法进行改进,提出AFP-tree算法,运用遍历中先序遍历的思想读取FP树,使取得频繁1-项集的全部条件模式基仅需要扫描1次FP树,AFP-tree算法产生条件模式基主要包括以下6个步骤:
1)搭建通用路径(CP)并将初值设定为空,扫描结点x5,此时CP内存储的是x5的前缀路径,因为CP现在为空,所以x5的条件模式基同样为空。
2)将x5存入CP,然后扫描结点x10,此时SP存储的是x10的前缀路径,所以x5是x10的1个条件模式基的1个条件模式基,支持度计数4,记为x5:4。
3)将x10存入CP,更新CP内容为x5x10。接着扫描x2,此时CP存储的是x2的前缀路径,所以x5,x10是x2的条件模式基,支持度计数3,记为x5,x10:3。
4)将x2存入CP,更新CP内容为x5x10x2。接着扫描x6,同步骤2)~3)可得出x6的前缀路径,继续扫描可得到x8的前缀路径为x5,x10,x2,x6,x9,x4,x7:1,此时发现x8为终端结点,返回至最近分支处,遍历未被扫描的分支结点x9,同时CP内容更新为x5x10x2x6。
5)继续扫描x9的另一个子结点x12,得到x12的1个条件模式基x5,x10x2,x6,x9:1,同时更新CP内容为x5x10x2x6x9x12,然后扫描x15,得到x15的1个条件模式基x5,x10,x2,x6,x9,x12:1。
6)继续扫描发现,x15是叶结点,返回到未被扫描的分支结点x10,以此类推,可全部扫描树中剩余的子结点,并最终得到全部的条件模式基,见表4。

表4 通过条件模式基寻找频繁模式Table 4 Finding frequent patterns by conditional pattern bases
AFP-tree算法对树进行扫描即运用先序遍历的思想,只需对FP树所有结点扫描1次,便可获得数据中所有频繁1-项集的条件模式基,其中,算法的复杂度包括时间复杂度和空间复杂度,与树的节点数一致,均为O(n),n为FP树全部结点的数目。
本文采取实时剪枝的方法,仅保留满足支持度的频繁项集,将不满足支持度阈值的项删除,建立去冗余的条件FP树,如图4所示。
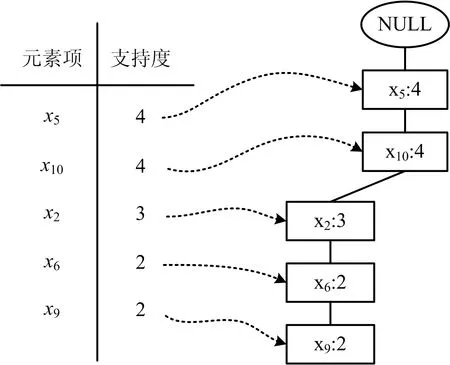
图4 条件FP树Fig.4 Conditional FP-tree
从表3及图4的挖掘结果中,获得频繁模式:(x5,x10,x2,x6,x9:2),可确定x5,x10,x2,x6,x9之间为强关联规则,即车门、晚点、上行、故障、终到之间存在强关联规则,进一步得到(x5,x10:4),既车门、晚点之间存在更强的关联规则。当挖掘的样本量足够大时,可出现更多的频繁项集,进一步可得到完整的规则,最终得到造成地铁运营风险事件的关键危险源。
3 算例分析
3.1 数据描述
地铁运营调度日志由车站调度工作人员,在地铁运营活动过程中实时记录的某些情况发生时车站工作人员的行为、动作及事件状态的文本描述,其中包括正常事件和险性事件相关的描述。本文文本挖掘的原始数据为某地铁公司运营线路的2017—2019年地铁运营调度日志。其核心字段“content”是对事件内容进行客观记录的字段。
3.2 实验环境
实验平台选取Intel(R) Core(TM) i5-10210U CPU 2.11GHz、16G内存、Windows10、64位操作系统,数据处理在Pycharm软件中运用Python语句完成。
3.3 基于改进Apriori算法的危险源挖掘
1)数据预处理
首先对地铁运营日志原始数据中的干扰数据进行清理,从102 834条原始数据中得到38 465条与造成运营风险事件有关的数据,去除干扰数据,结果见表5。
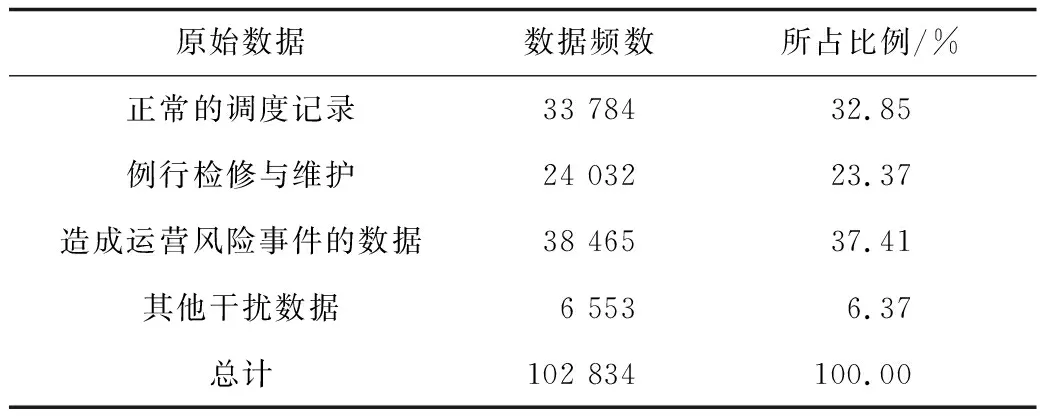
表5 数据去干扰结果Table 5 Results of data de-interference
运用Jieba库对去干扰后的数据进行分词及去停用词操作,并对得到的数据进行词向量的嵌入,预处理后的数据见表6。
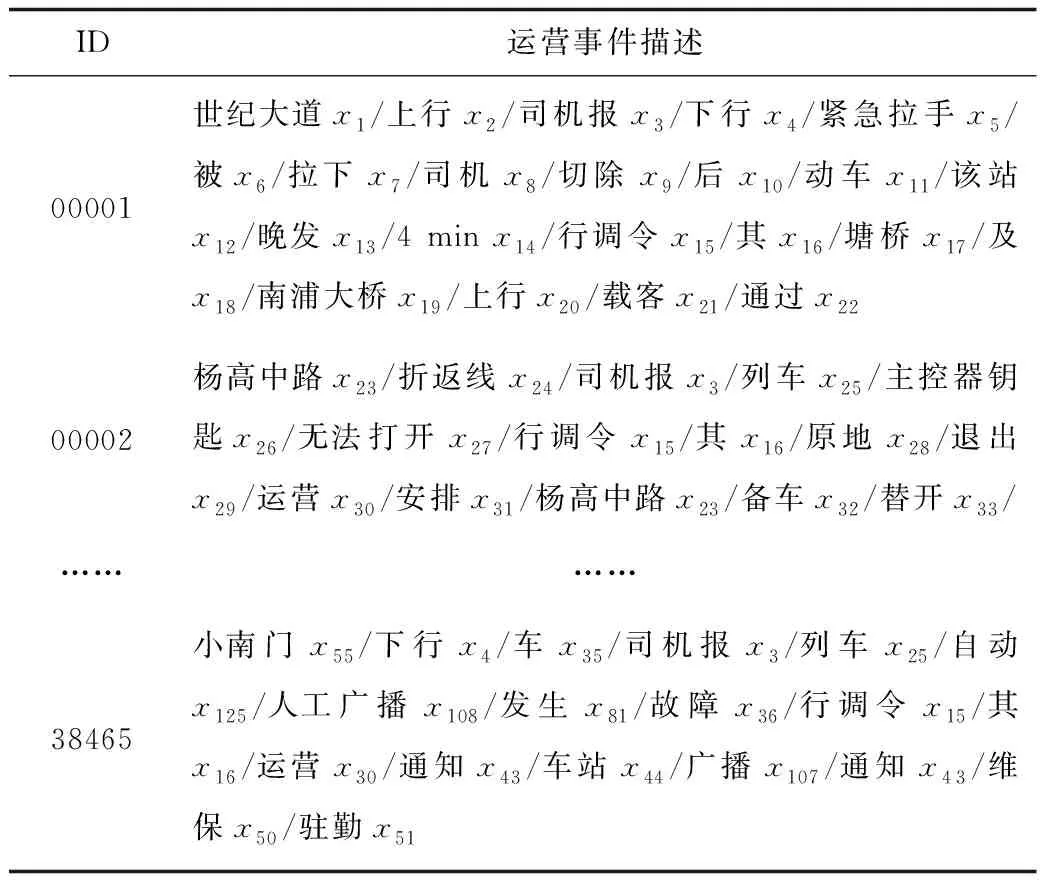
表6 预处理后的数据描述Table 6 Data description after preprocessing
2)数据分析
将经过预处理后的运营日志数据输入AFP-tree算法中,运用Pycharm运行工具进行数据分析,得出最终的事务频繁模式,由于最终的事务频繁模式规模较大,本文仅选取部分模式作为展示,见表7。
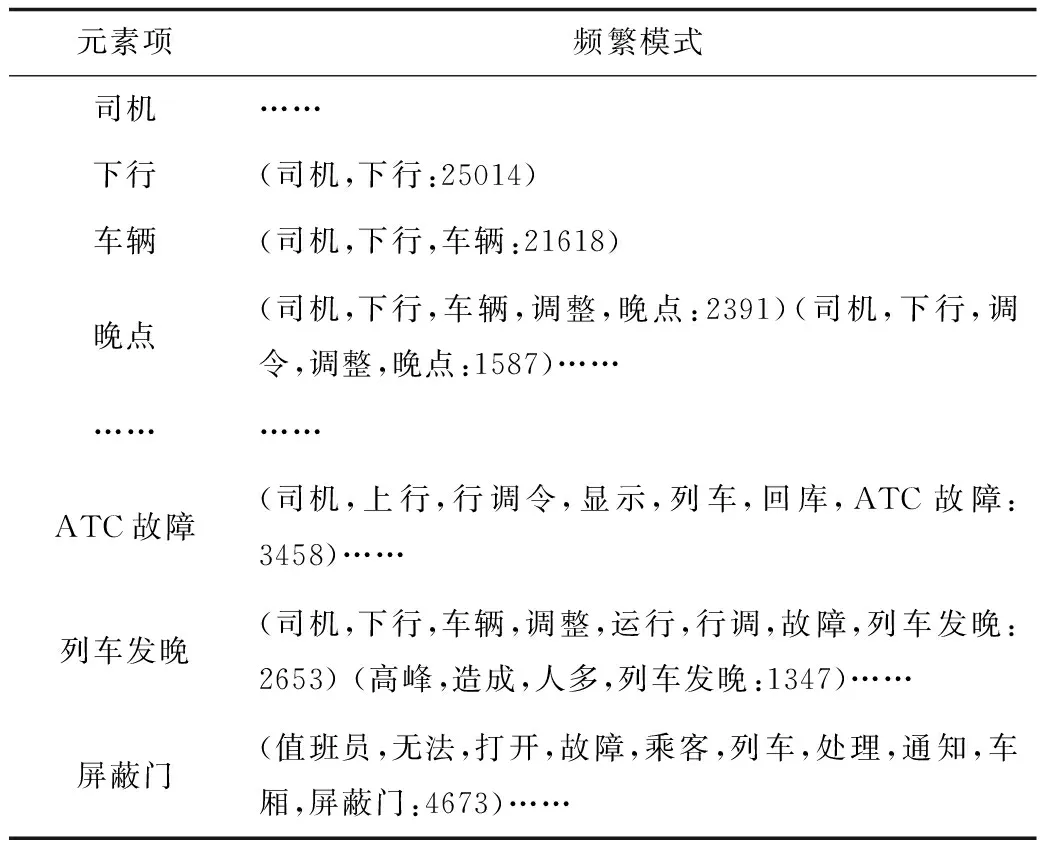
表7 最终的事务频繁模式Table 7 Final transaction frequent pattern
通过AFP-tree算法计算得出各个关联规则的置信度,通过多次实验对比,本文数据在设定支持度为20%、置信度阈值为60%时,实验可以取得较为理想的效果。
取置信度超过阈值的危险源为关键危险源,通过计算共辨识出25种关键危险源,计算结果输出以词云形式展现,如图5所示。图中字号越大,字体颜色越明显,表示该危险源的置信度越高。置信度越高,表示该危险源导致风险事件的概率越大,需要重点防范与控制。

图5 关键危险源词云Fig.5 Words cloud of key hazard sources
根据置信度对25种关键危险源进行分级,见表8。以10%为1个间隔,共将危险源划分为4个等级,I级表示最高等级,该范围内的危险源需要重点防范与控制,Ⅳ级表示关键危险源分类后的最低等级,但仍然需要格外关注,防范其发生危险,以及与其相关的其他衍生危险事件。

表8 关键危险源等级划分Table 8 Classification of key hazard sources
根据对地铁运营调度日志的关联规则进行分析,挖掘出的25种危险源中,主要集中在车辆、通号以及客观原因(大客流、屏蔽门夹人、夹物等)中,进一步通过对关键危险源的分级,针对不同等级的危险源实施有区别的管控办法。针对Ⅰ级危险源,应该对其实施重点管控,具体包括车门、屏蔽门、广播、VOBC此类置信度高、易发危险的设施部件,同时注意由于天气原因、重要节假日等导致的大客流问题;Ⅱ级与Ⅲ级危险源,主要为系统、硬件设备故障问题,可根据其具体故障频次,结合某一硬件故障所导致的后果(主要以该车辆或者相关区域是否可以继续运营为依据),安排定期巡检、更换、维修等措施,预防危险的发生;针对Ⅳ级危险源,主要注意地铁运营时车辆和车站内的乘客动态,系统及硬件问题可结合Ⅱ级与Ⅲ级危险源的处理办法,同时车站工作人员要密切注意站台乘客动向,尤其在客流量较大时,注意防范意外风险的发生。
3)改进算法与原算法效率对比
为验证本文算法改进的有效性,选取10万条未去除干扰数据的地铁运营调度日志数据作为实验数据,对FP-growth、Apriori和AFP-tree算法分别验证其计算时间。实验中每项数据由计算机运行8次后取平均值得出,在一定程度上避免由于计算机本身原因出现的偶然结果。
3种算法在数据类型和数据量完全相同条件下,支持度发生变化时算法的运行时间对比如图6所示。对比最小支持度设置为0.1的条件下,样本数据库中数据规模逐渐增加时,3种算法的计算时长对比如图7所示。由图7可知,当实验条件相同时,改变唯一变量,AFP-tree算法耗时更短,所以AFP-tree算法在挖掘关联规则时有更好的效率优势。
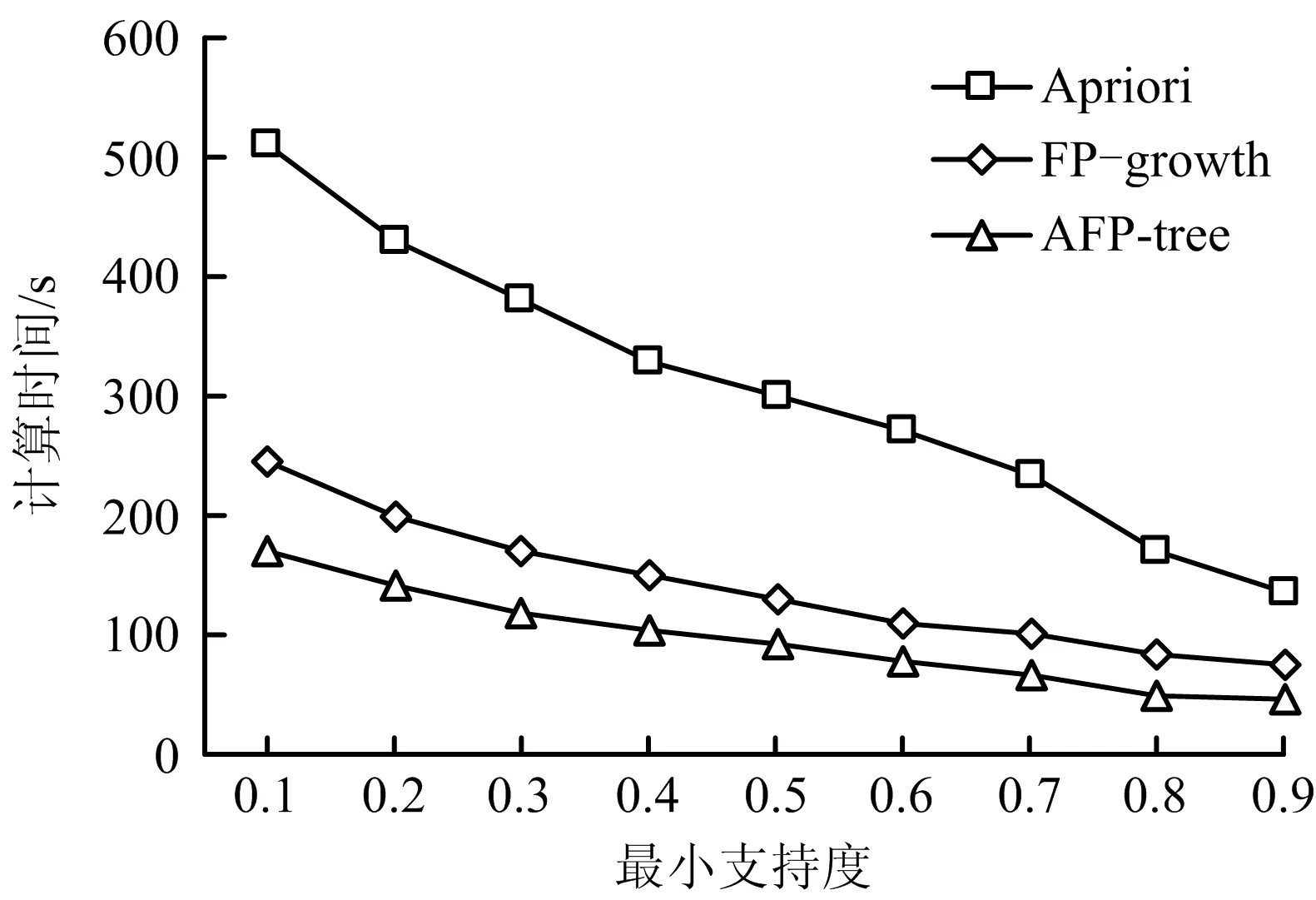
图6 不同支持度下的算法效率对比Fig.6 Comparison of algorithm efficiency under different support degrees
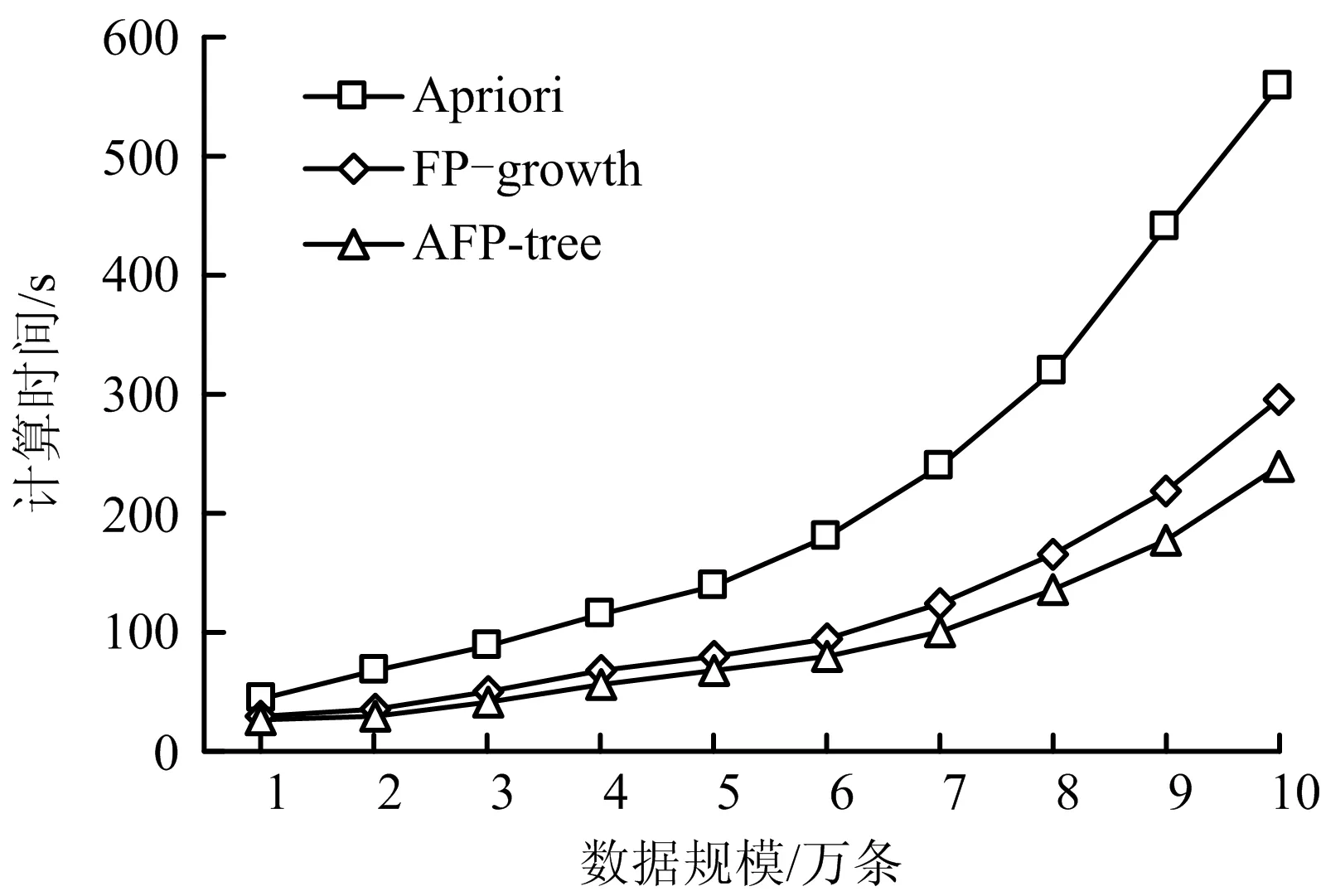
图7 不同数据规模下的算法效率对比Fig.7 Comparison of algorithm efficiency under different data scales
4 结论
1)通过构建AFP-tree算法,对地铁运营日志中的危险源进行深入文本分析,挖掘其中关键危险源并进行分级管控,通过实例证实该算法可有效应用于地铁轨道交通危险源辨识工作中,对于实践有现实指导意义。
2)通过实验对算法的效率提升进行验证,改进之后的算法相较于传统算法效率得到有效提升,且数据规模越大、支持度越小时,算法效率优势越显著,可以对大规模的文本数据进行分析计算。

