基于HMM和DT的无人机异常检测方法*
张洪海,周锦伦,于文娟,刘 皞,钟 罡
(南京航空航天大学 民航学院,江苏 南京 211106)
0 引言
近年来随着我国低空空域不断开放,低空无人机在航拍、物流、救援等领域的应用随之兴起,与此同时,由无人机造成的安全事故,如无人机失联、失控甚至坠落造成人员伤亡的情况也频繁增加。及时检测并识别无人机异常状态,可以提前对可能发生的事故做出预警甚至规避。因此,如何实时、快速、准确地识别无人机异常状态,成为提升无人机运行安全性的1项重要课题。
目前,许多专家学者在无人机异常检测方向进行了深入研究并取得优质成果。2015年,Schumann等[1]通过添加硬件传感器的方法对无人机速度、航向等运动参数进行实时监控,以此识别无人机异常状态;何永福等[2]于2016年首次提出了1种基于过采样投影近似基投影追踪(OSABP)的无人机异常检测方法,其ROC曲线下方面积(AUC)分数高达0.98,检测准确率达到较高水平;2017年,陈亚峰[3]引入K-means聚类的方法建立了无人机异常检测模型,并开发了较全面的无人机实时异常检测系统。2020年,韩鹏等[4]通过建立贝叶斯网络模型对无人机失效致因进行分析,首次用概率理论证明了外界风和无人机自身电池是导致无人机失效最可能的原因;同年,刘连胜等[5]引入旋翼无人机动力学模型,提出1种生成旋翼无人机异常数据的方法,并采用典型相关性分析验证了所生成异常数据的合理性。
对于无人机的异常状态检测,大多通过对无人机运动数据进行分析,从而精确地识别无人机的异常状态,但目前在无人机异常状态分类、异常严重程度识别等方面的研究仍有不足,即无法根据识别的无人机异常状态明确相关反应措施,如:由于短暂地面阵风导致的无人机运动异常,通常可以通过控制指令解决,而电池失效、通信失效等硬件问题,则必须采取紧急措施。除此之外,无人机异常检测方法的实时性(时间复杂度)仍有一定的提升空间[6-8]。
出于对上述问题的考虑,本文提出1种基于隐马尔可夫模型(HMM)和决策树(DT)的无人机异常检测方法,在识别无人机不同异常状态的同时改进无人机异常检测的计算复杂度,提升无人机异常检测的实时性。
1 无人机异常
无人机异常,一般是指无人机失控、失联。包括由于外界风向、风速、降水等气候原因导致无人机运动受到干扰,或电磁环境异常导致的无人机通信失效,以及无人机自身动力系统、通信系统、操作系统异常导致的无人机失控[9-11]。
无人机运行环境通常处于低空或中低空,由于气象条件多变、电磁环境复杂,无人机在运行过程中受到各种随机因素干扰导致无人机异常,本文称之为干扰异常,其特征为无人机运动状态与期望运动状态出现短暂的轻微不符,一般可通过正确操作恢复。而由于无人机自身飞行控制系统出现故障所导致的无人机异常,本文称之为硬件异常,其特征为无人机运动状态与期望状态长时间严重不符,一般无法通过操作命令恢复正常状态,无人机异常状态分类如表1所示。
根据无人机事故致因的历史数据和事故致因理论分析[4]可以发现,无人机出现失联、失控、坠毁的严重事故,大多数是由于无人机自身硬件系统故障导致,而寻常阵风扰动导致的干扰异常,通常不会对无人机运行安全产生较大影响。因此,准确地从无人机异常状态中区分出无人机硬件异常并采取针对措施,对提升无人机运行安全水平十分重要。
2 无人机异常检测方法(HMMDT)
2.1 无人机异常检测方法
隐马尔可夫模型(HMM)是动态贝叶斯网络(Dynamic Bayesian network)的1种类型,假设无人机运行时后1状态仅与前1状态有关(满足马尔可夫性),则无人机运行的下1状态仅由无人机当前运动状态决定[6]。采用隐马尔可夫模型进行无人机时序建模的主要优点在于:一方面,可以联系相邻时刻间无人机运动状态,即无人机各个时刻异常检测结果之间不再被孤立;另一方面,通过计算各个状态之间的转移概率,可以提取无人机运行状态变化之间的长期特征,为无人机异常状态分类提供具体的数值参考。
决策树(DT)是1种监督学习方法,即通过带标签的样本数据从多层if/else问题中寻找数值边界,生成模型后可以较快的速度得到分类结果。因此,采用决策树模型用于无人机异常检测,具有速度快、操作简单、泛化能力好等优点。
本文综合2种模型的优点,提出1种无人机异常检测方法,其基本思想为:先采用训练的决策树判断无人机运行状态是否异常,随后根据隐马尔可夫模型对该异常状态进行分类,进而实现对无人机实时异常检测与异常识别,无人机异常检测模型结构如图1。
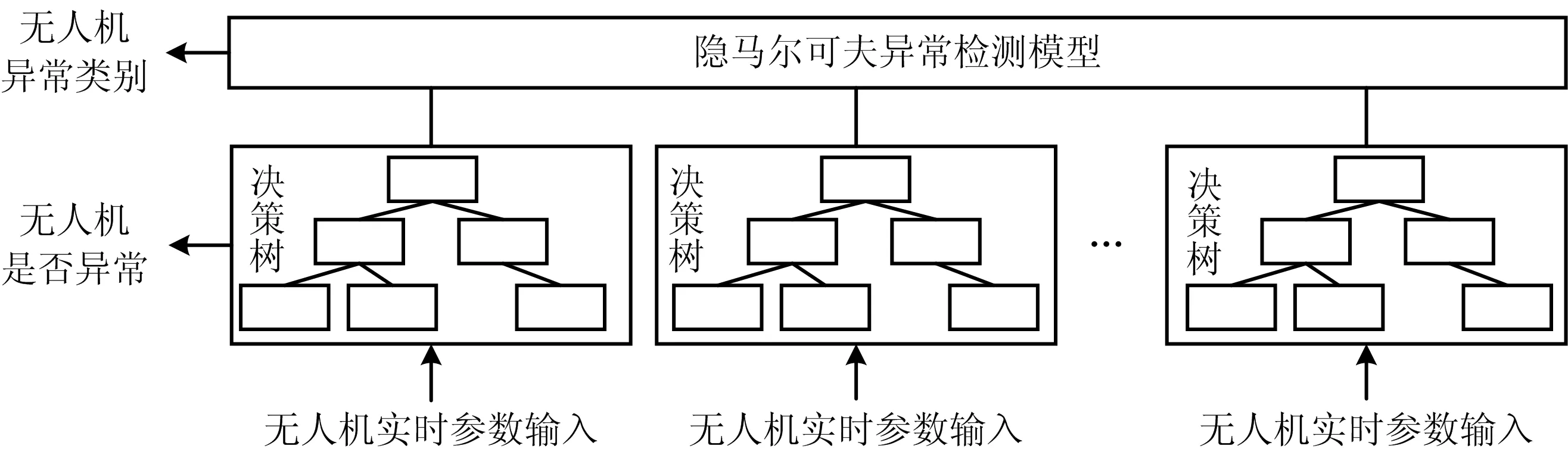
图1 异常检测模型结构示意Fig.1 Schematic diagram of anomaly detection model structure
2.2 参数定义
无人机运动参数矩阵Xt:Xt=[xt1,xt2,…,xt9]为1×9矩阵,包含无人机t秒水平速度大小、垂直速度大小、几何高度等无人机运动参数,如表2所示。
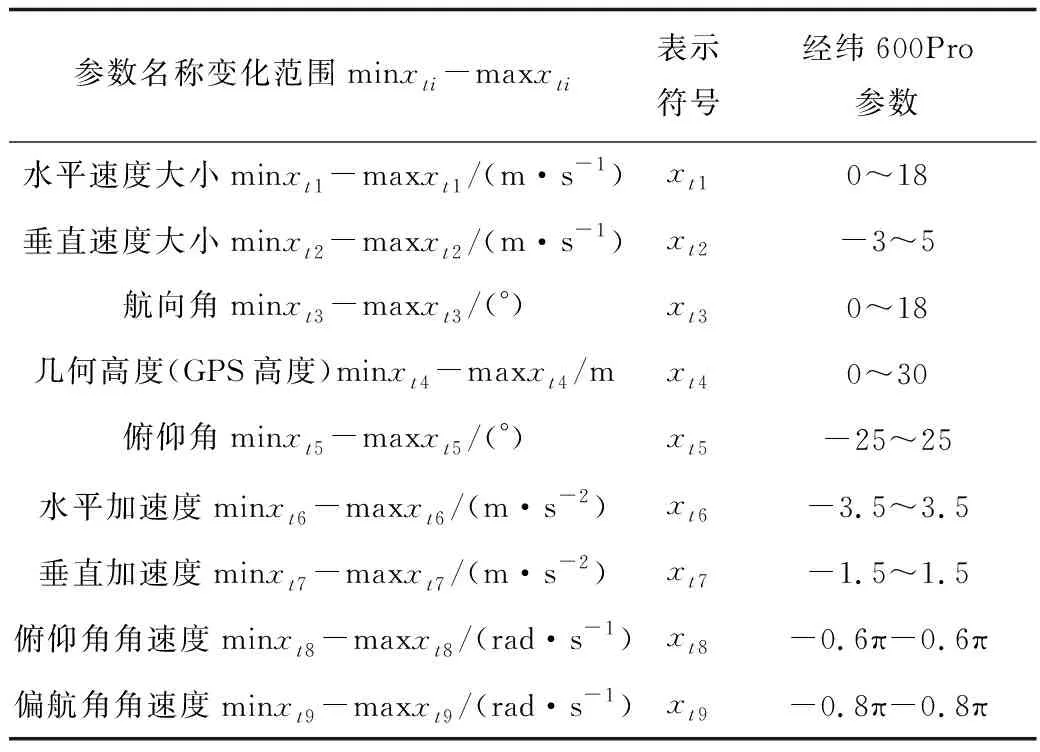
表2 需要设置的无人机性能参数信息Table 2 Performance parameter information need to be set for UAV
无人机控制参数矩阵Ct:Ct=[ct1,…,ct(n-1),ctn]为1×9矩阵,表示第t秒对应无人机运动参数的控制指令,如:c56表示无人机运行第5秒对水平加速度的调整,调整大小为|c56|。
无人机状态标签yt:yt为0-1变量(异常标签),0表示无人机状态正常,1表示无人机状态异常。
无人机参数矩阵Wt:Wt=[Xt,yt,Ct]为1×19矩阵表示第t秒无人机所有运动参数和控制参数以及异常标签。
无人机异常类别标签zt:zt为0-1变量(异常类型标签),0表示无人机异常类型为干扰异常,1表示无人机异常类型为硬件异常。
TP表示无人机运动状态异常,被检测为异常的样本数量;FP表示无人机运行状态异常,被检测为正常的样本数量;FN表示无人机运行状态正常,被检测为异常的样本数量;TN表示无人机运行状态正常,被检测为正常的样本数量。
2.3 模型训练数据获取
考虑到安全、成本等因素,本文使用软件模拟无人机的运动生成相应模型训练数据,在XPlane模拟飞行平台上设定相关无人机性能参数,构造相应的无人机模型,主要性能参数如表2。
设定阵风到达率、风向风速分布情况,将模拟无人机升空后操控一段时间,记录每秒产生的无人机运动数据,作为后续决策树训练数据集。重复上述操作以获得更多的模型训练样本,并根据操作人员观察的无人机运动状态为数据添加干扰异常标签,随后将训练数据作最大-最小标准化处理。
2.4 无人机异常检测模型构建
1)隐马尔可夫时序模型参数确定
无人机运行初始状态yt=1:无人机起飞前需要检查各项硬件状态以及通信连接以保证无人机的适航性,故可认为无人机初始状态P(yt=1=0)=1。
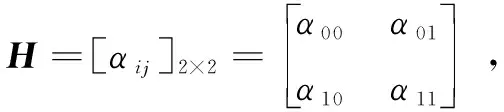
(1)
式中:αij为无人机的状态转移概率;yt+1和yt分别为无人机t+1时刻状态和无人机t时刻状态;k(yt+1,yt)为无人机从状态yt转移到yt+1的样本频次计数,次;aij的含义为:在t时刻,若当前无人机状态为si,则下一时刻状态为sj的概率;H=[aij]2×2为无人机状态转移矩阵,反映无人机运行时各个状态之间转化的长期规律[12]。
2)决策树模型构建
训练决策树模型[13-15],样本输入参数为Xt,目标参数为yt,以基尼不纯度(Gini Impurity)最小作为模型训练指标,构建无人机干扰异常状态检测决策树模型,基尼不纯度G(k)如式(2)所示:
(2)
式中:k为决策树第k个节点;c为分类数目(本文c=2);pk为决策树第k个节点中第j类样本比例。G(k)越小,表明节点k样本纯度越高,决策树训练效果越好。
由于多维数据的决策树模型训练会出现过拟合(over-fitting)现象;且由于选择的无人机运动参数之间存在一定相关性,导致训练样本数据冗余。因此,需要提取与异常标签相关性较强的参数,控制决策树的复杂度以提升计算效率,同时提高验证集精确率,减少过拟合。因此以验证集精确率为目标,采用比较决策树特征重要度(feature importance)的后剪枝(post-pruning)策略。记该异常检测决策树模型为Tree。
3)无人机异常状态分类
基于无人机第t秒的参数向量Wt=(Xt,yt,Ct)获得无人机t+1时刻参数矩阵Wt+1=(Xt+1,yt+1′),有(Xt+1=Xt+Ct,yt+1′=Tree(Xt+1)),其中,yt+1′表示由运动参数向量Xt+1预测t+1时刻无人机运动状态。
定义异常度η衡量无人机t+1秒实际运动参数与t+1预测运动参数的偏差程度,如式(3)所示:
(3)
式中:X*t+1为t+1秒标准化后的无人机运动参数;X*t+1′为t+1秒标准化后基于t秒数据预测的无人机运动参数,r(X)表示矩阵X元素个数。
设定ηnormal为无人机异常度阈值,若η>ηnormal则记为无人机运行状态异常,若η<ηnormal则记为无人机运行状态正常。
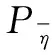
(4)
式中:α01为无人机运行时受到干扰导致其状态从正常到异常的概率,α11为无人机状态继续保持异常状态的概率,FP/(TP+FP)表示异常检测决策树误检率。式(4)表示无人机正常状态下出现这种连续状态为异常的情况的概率小于ε,因此,一旦该情况出现,应当认为无人机发生硬件异常。综上所述,无人机硬件异常判定标准如式(5)所示:
(5)
式中:ηt为第t秒无人机异常度,ηnormal为设定的无人机异常度阈值。
3 实例验证
3.1 样本获取与超参数设置
根据2.2获得训练数据,设定阵风到达率服从期望方差均为λ=15 s的泊松分布,阵风大小服从均值为μ=2.5 m/s,方差σ2=4的正态分布(模拟现实低空风的情况),重复操作,获得5 000个实验样本,其中干扰异常样本386个,基于隐马尔可夫模型获得其状态转移概率矩阵:
设置超参数ε=0.001,k=3,ηnormal=0.3,当无人机连续k=3个时间段η(即ηt和ηt+1)大于设定值0.3时,满足式(4),进而根据式(5)进行异常分类。
3.2 训练决策树子模型
经纬600pro无人机性能参数如表2所示,采用软件模拟上述性能参数无人机进行2.4中步骤,获得异常检测的决策树,表2中9个运动参数的决策树模型特征重要度如下图2。
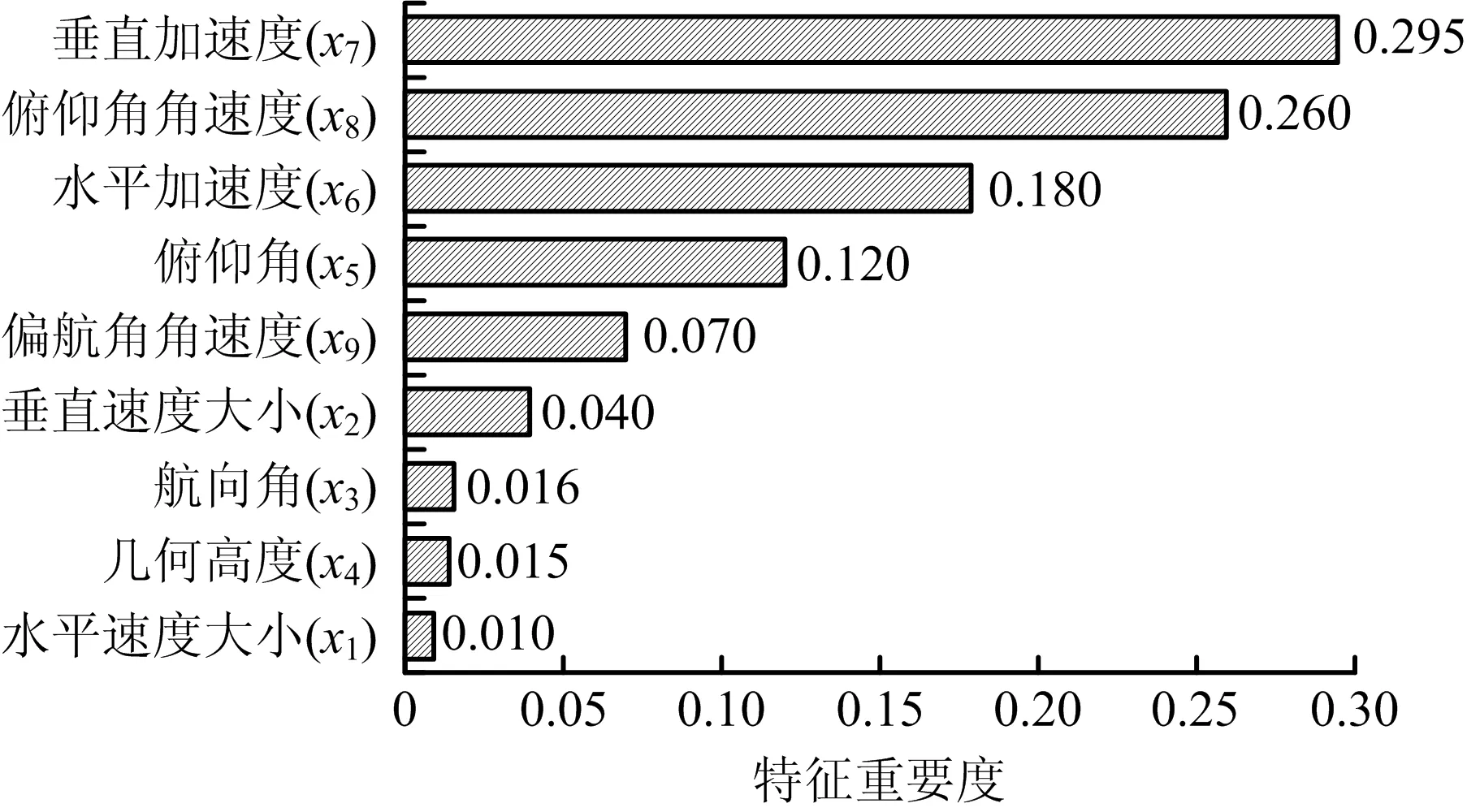
图2 无人机运动参数特征重要度Fig.2 Feature importance of UAV motion parameters
通过调整训练集和验证集比例,并根据重要度筛选异常检测特征参数不断剪枝,选取验证集精确率PPV作为优化指标,PPV计算如式(6)所示:
(6)
实验测得:当训练集占总样本60%且删除4个运动状态参数时测试集样本的分类精确率最高,达85.1%,决策树模型验证集精确率变化如图3。
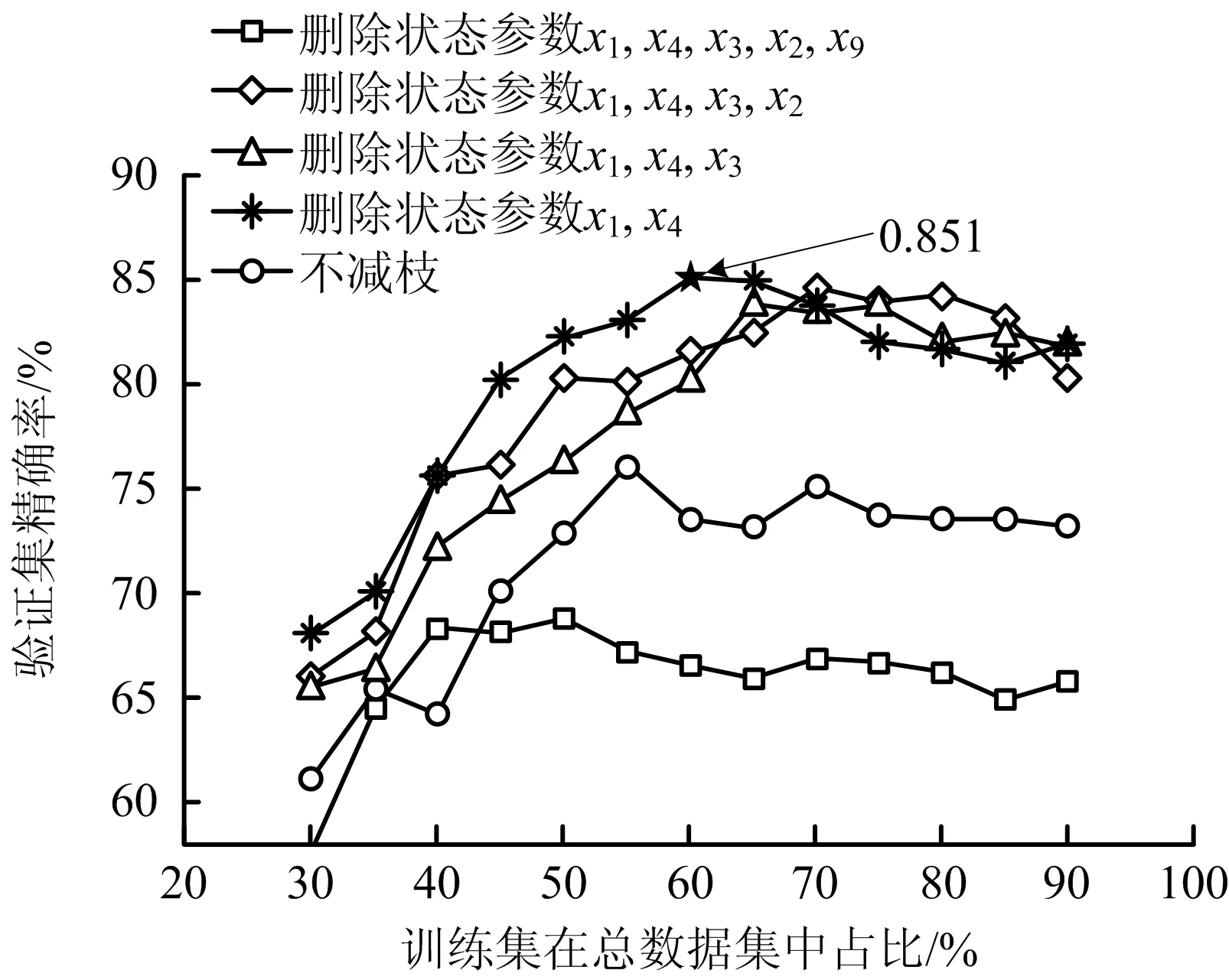
图3 决策树模型测试准确率变化Fig.3 Change of test precision by DT model
删除其中特征重要度较低的参数(几何高度、水平速度大小、航向角、垂直速度大小)完成后剪枝,重新训练决策树,剪枝后的决策树记为Tree。
3.3 异常检测真实飞行实例验证
实验机型经纬600pro配备有GPS、ADS-B、无人机操作系统等软硬件,由ADS-B提供实时运动参数,无人机遥控器向无人机控制系统提供实时控制参数。为便于验证图3中决策树模型所判断的干扰异常是否正确,将无人机升空后保持1.5 m高度悬停,共持续2 300 s,获得2 300个实际运行产生的无人机运动数据。人工监视无人机所受外界阵风影响的时刻,计数得无人机运行时存在阵风干扰的时刻为131 s,决策树模型所识别干扰异常时刻121 s,无人机运行最后阶段由于无人机电量不足,导致遥控指令失效,从而被识别为硬件异常,硬件异常总时长为17 s,硬件异常识别15 s,记混淆矩阵M(2×2):

计算召回率R、特异度TNR、准确率P如式(7)~(9)所示:
R=TP/(TP+FN)
(7)
TNR=TN/(TN+FP)
(8)
P=(TN+TP)/(TN+TP+FP+FN)
(9)
干扰异常和硬件异常总召回率R=92.9%,特异度TNR=2.49%,准确率P=97.2%,无人机运行中的相关参数变化如下图4。
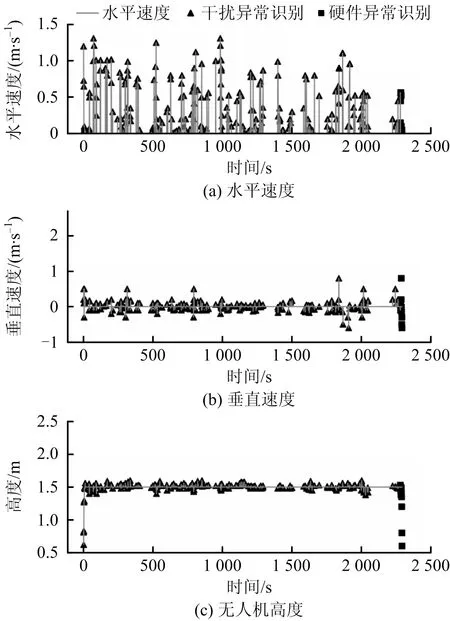
图4 无人机速度高度随时间变化曲线Fig.4 Variation curve of UAV speed and altitude with time
4 对比分析
分别采用HMMDT、贝叶斯网络(Bayesian Network,BN)、典型相关性分析(Canonical Correlation Analysis,CCA)、K均值聚类(K-means)对上述实验数据集进行异常检测,得各个方法的ROC(Receiver Operating Characteristic)曲线如图5。
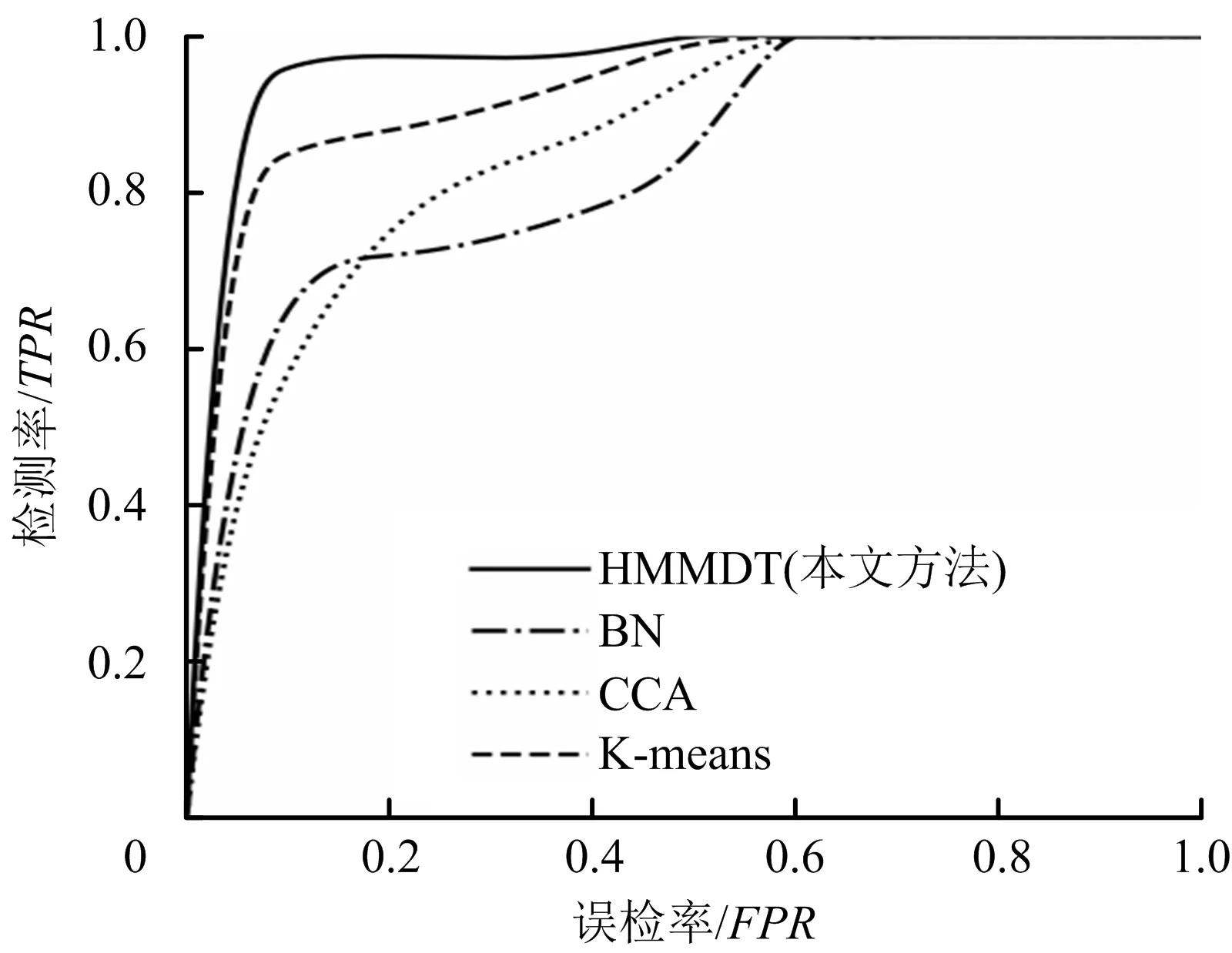
图5 各方法ROC曲线对比Fig.5 ROC curve comparison of each method
其横坐标为误检率(False Positive Rate,FPR),纵坐标为检测率(True Positive Rate,TPR),计算ROC曲线下方面积AUC;本文方法的AUC相比于其他异常检测方法均有所提高,如表3所示。
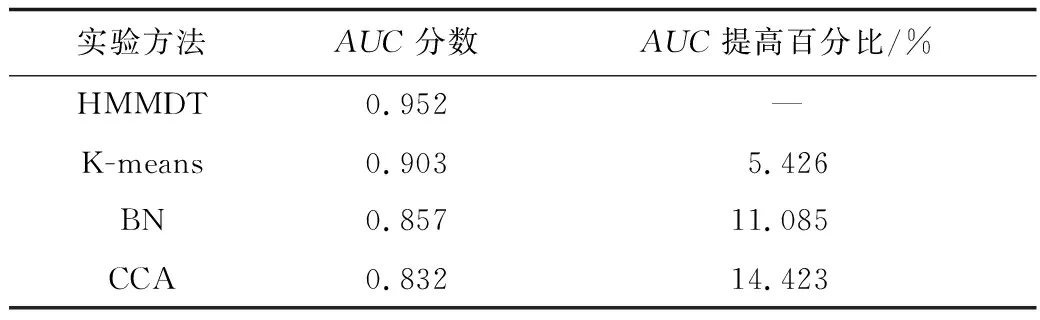
表3 各方法AUC分数对比Table 3 AUC score comparison of each method
为进一步验证该异常检测方法的适用性,分析该方法的计算复杂度,并与其他异常检测方法对比。其中m为输入矩阵长度(维数),r为输入矩阵宽度(向量个数),l为提取状态特征参数数目,k为K-means聚类中心数目,s为存储的时间序列长度,各方法复杂度如表4所示。

表4 各方法计算复杂度对比Table 4 Comparison on computational complexity of each method
本文方法有着较低的时间复杂度,这意味着该方法异常检测的实时性更强,采用3.1中参数实验,单次异常检测与分类仅用63 us(i5-6400CPU),可以满足无人机实时异常检测需要;虽然由于决策树原理导致该方法有着指数形式的空间复杂度,但由于无人机运动状态参数较少,即使指数形式的空间复杂度仍可被无人机内存所接受,且在应用中可以通过减枝等手段降低决策树空间复杂度。
5 结论
1)提出HMMDT无人机异常检测方法,旨在实时检测无人机异常并识别异常类型。首先将无人机异常状态分为2类,即干扰异常和硬件异常;构建基于HMMDT的异常检测模型,并根据2种异常特征定义无人机异常度作为异常分类标准,实现对无人机实时异常检测并识别无人机异常类型。
2)采用经纬600Pro型无人机作实操验证,该方法对无人机运行时异常状态的检测具有较高的准确率,且能够准确识别由于环境的不确定性导致的短暂干扰异常和由无人机系统故障导致的硬件异常,相比于K-means,BN,CCA等异常检测方法,HMMDT具有较小的时间复杂度和较高的检测准确率,可以在准确识别无人机异常状态的同时区分出异常类型。除此之外,上述方法理论上可适用于其他无人机型号,且流程简单、易于实现,其算法复杂度可以满足无人机实时异常检测需要。

