开孔双层球面网壳结构的优化设计分析

刘 娟，杨 宁，2，孙 韬，3

（1.江苏建筑职业技术学院 建筑建造学院，江苏 徐州 221116；2.山东省土木工程防灾减灾重点实验室，山东 青岛 266590；3.江苏建筑节能与建造技术协同创新中心，江苏 徐州 221116）

网壳结构因为受力合理、结构稳定性好，造型既轻巧灵活又能适应堆煤取料机（斗轮机）的工艺界面，被广泛应用于储煤仓等工程中。通常情况下，球面网壳结构受力较均匀，传力路径简单明确，便于设计和施工。但是，当网壳结构开有孔洞时，原有的传力路径被破坏，开设的不对称孔洞将对结构各方面性能产生不利影响。国内已有较多的开门洞网壳实例，其构造措施也较完善，研究成果不少，但是针对在网壳其他位置开设孔洞的研究尚少，且对落地开孔网壳的优化研究较匮乏。因此，应用ANSYS 参数化设计语言（APDL）进行编程，保持网壳跨度不变，以结构用钢指标为目标函数，以网壳矢高、网壳厚度和杆件截面为设计变量进行优化设计，并分析各因素对用钢指标的影响规律和影响程度，便于此类网壳施工时采取安全合理的构造措施。

1 工程概况及有限元模型建立

1.1 工程概况

某火力发电厂干煤棚结构形式为双层正放四角锥球面网壳，根据生产工艺要求，网壳侧部开有孔洞，见图1。工程基本信息如下：跨度87.00 m，厚度2.71 m，矢高29.21 m，上弦设置17 环，下弦设置18 环，上弦网格节点在第2、4、7 环进行加密，加密形式为“1 分2”，最外环节点数为72。网格划分情况见图1 ～图5 及表1。采用固定铰支座隔点布置方式，共计36 个。网壳支承结构采用钢筋混凝土独立柱，柱截面尺寸为400 μm×600 μm，柱高10 m，混凝土强度等级C30。杆件选用GB700[1]中 的Q235B 钢，Ø48×3.5、Ø60×3.5、Ø75.5×3.75、Ø88.5×4、Ø114×4、Ø140×4、Ø159×6 和Ø168×6 八种截面。结构安全等级为二级，重要性系数取1.0。

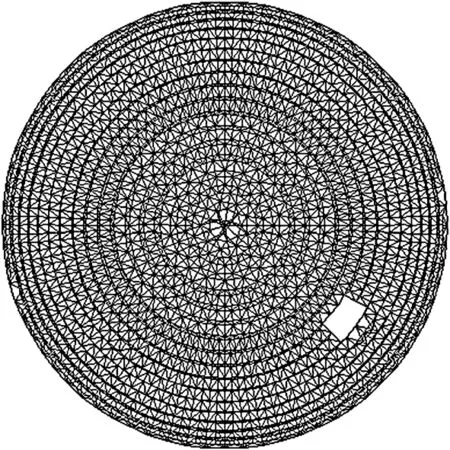
图1 模型俯视图

图2 模型侧视图

表1 网格划分列表

1.2 孔洞开设位置

孔洞开设在第10 环和11 环，径向和环向各跨越两排杆件，在上弦占据九个网格，在下弦占据12个网格，见图3、图4。其水平投影面积（网壳上弦）为58.71 m2，洞口切平面投影面积（网壳上弦）为75.28 m2，孔洞投影尺寸见图5。

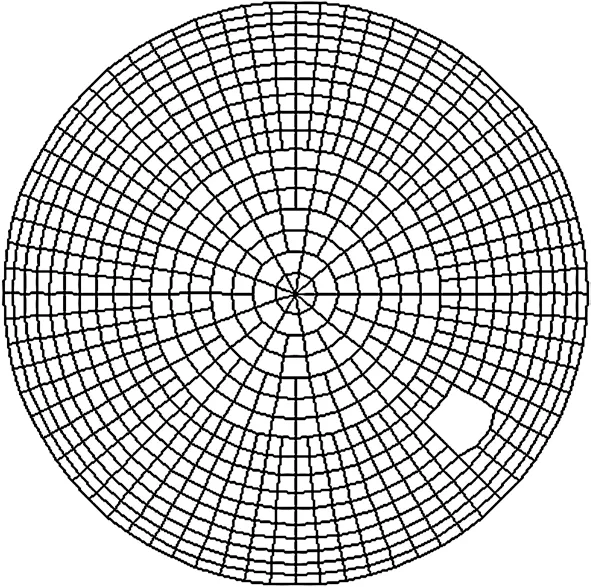
图3 上弦俯视图

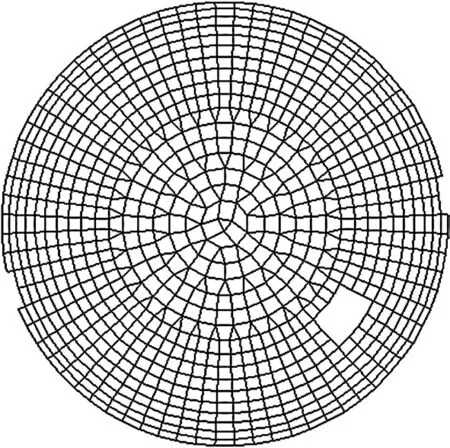
图4 下弦俯视图

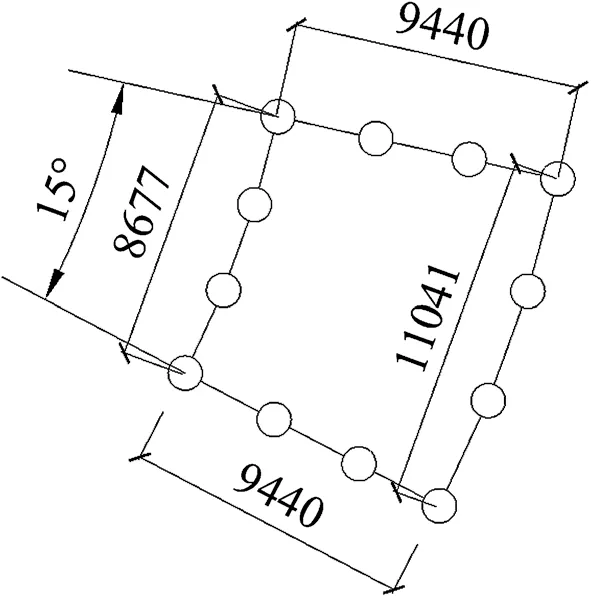
图5 孔洞切面投影（mm）

1.3 结构仿真计算假定

（1）按照《空间网格结构技术规程》第4.1.4 条“分析网架结构和双层网壳结构时，假定节点为铰接，杆件只承受轴向力”[2]，故本网壳工程在建模时假定所有杆件均为纯铰接杆，所有节点均为空间铰接节点，由此杆件只承受轴力，并按弹性阶段进行分析。

（2）网壳结构的荷载均按静力等效原则化为作用于节点上的集中荷载。

（3）采用LINK8 单元模拟[3]，该单元只承受轴力，不承受弯矩，每个杆端三个自由度。

1.4 结构仿真建模主要参数

网壳结构分析用阻尼比取0.03。本网壳杆件均采用Q235B 圆形钢管，控制钢管壁厚≤16 mm，钢材的机械性能参数均按《钢结构设计标准》GB50017-2017[4]取值。模型计算时按照控制应力比0.9 控制杆件截面，最小截面取Ø48×3，杆件截面由程序自动优选。网壳的支座竖向采用固定约束，即竖向刚度取无限大，水平两方向均采用弹性约束，其中弹簧刚度取值参考文献[5]的分析结果，取为2k N/mm[5]。根据本网壳实际及《空间网格结构技术规程》的相关规定，建模时考虑自重、活荷载、风荷载、雪荷载、温度荷载、地震荷载等荷载，并按《建筑结构荷载规范》GB 50009-2012[6]进行规范取值与荷载组合。

2 结构优化设计过程

2.1 优化思路

空间网格结构的优化设计通常以结构自重（即用钢量）最小作为目标函数，而网壳结构的稳定性是结构设计中的重要问题，故对网壳优化设计的同时须对其稳定性加以校验[7]。在结构优化计算过程中，不改变网壳的跨度、网格布置和荷载情况，取钢管外直径D 和壁厚t、网壳矢高F 和网壳厚度h 为设计变量，利用ANSYS 优化模块，编写优化程序，进行100 次计算循环，得到以用钢指标最小为目标函数的最优解。

2.2 结构优化设计的一般数学表达式为[8]：

设计变量

满足约束条件

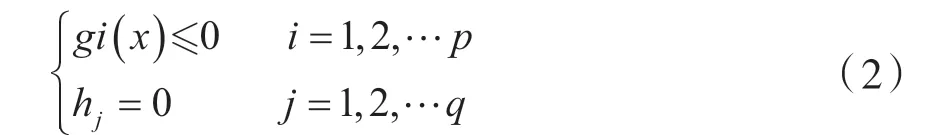
使目标函数

式（2）中由p 个不等式约束和q 个等式约束规定了问题的可行域。

用最优化方法求得一组设计变量

上式即为一个最优设计方案，称为最优设计点，对应一个最优目标函数值

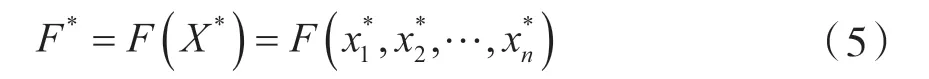
最优点和最优目标函数值两者构成了一个优化问题的最优解。

2.3 结构优化三要素

2.3.1 设计变量

有限元软件ANSYS 优化模块最多可设定20个设计变量[9]，结合本工程实际情况，在进行结构的优化过程中，共设置18 个设计变量，即：

（1）球面网壳的矢高F1，12.5 m ≤F1≤29.2 m。

（2）杆件外直径D2，D3，…，D9，50 mm ≤Di≤168 mm，i=2，…，9。

（3）杆件壁厚t10，t11，…，t17，3 mm ≤tj≤10 mm，j=10，…，17。

（4）网壳厚度h18，1.45 m ≤h18≤2.9 m。

2.3.2 目标函数

实际工程中往往将重量最轻或成本最低作为“最优设计”的标准[10-11]，故本工程将以杆件用钢指标最小为目标函数。

2.3.3 约束条件

约束条件又称为“状态变量”，是在结构优化设计过程中，对结构的设计变量所加的各种限制。本网壳在结构优化设计时设置了以下约束条件：

（1）网壳最大挠度

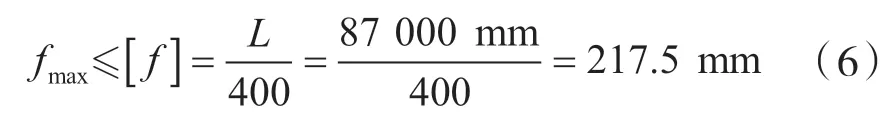
（2）杆件强度约束条件

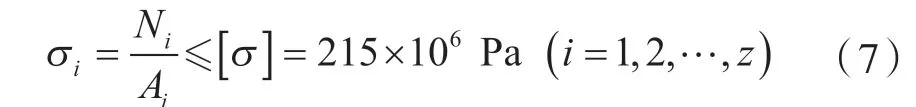
（3）杆件最小截面和壁厚限制

双层网壳结构杆件最小截面，参照现行的网壳结构技术规程JGJ61-2003 规定，取Ø50×3，即：

3 优化结果的分析与讨论

在优化计算中的两点说明如下：

（1）计算时考虑满跨均布荷载作用，且采用以活荷载控制下的荷载组合工况。

（2）网壳结构除杆件外的其他构件总质量为71 898 kg，包括螺栓球、螺栓、封板、锥头的质量。

图6 为本网壳结构各杆件截面的数量，优化过程仅改变了各杆件的截面面积，而并未改变各杆件截面所占有的比例。

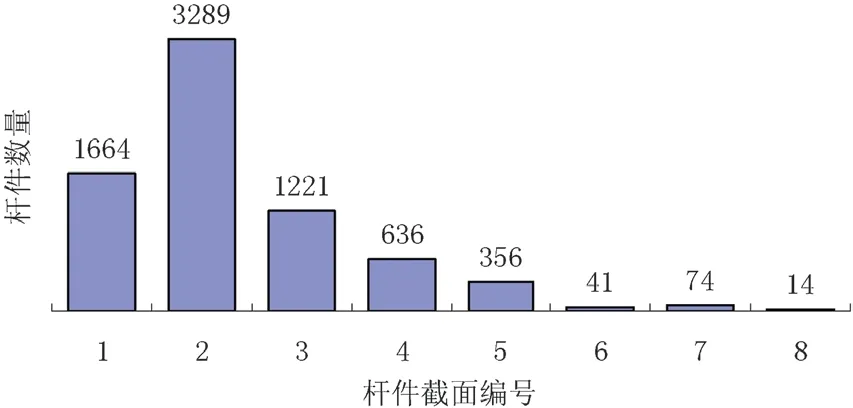
图6 各杆件截面的杆件数量

表2 为优化前后杆件截面变化情况。由表可以看出，杆件外径有明显增加，5～8 号杆件壁厚明显增大。在表3 中列出了优化前后截面面积的变化情况及目标函数值，优化后1～4 号杆件截面面积明显减小，而5～8 号杆件截面呈现增大的情况，但是由于本网壳结构中有90%以上杆件采用的是1～4 号杆件截面，因此，即使5～8 号杆件截面面积有所增大，结构的总用钢指标仍有明显下降。与原网壳结构相比较，网壳厚度减小0.9 m，网壳矢高减小3.3 m。优化后网壳杆件用钢指标为38.3 kg/m2，约为原网壳结构的71.6%，节省钢材28.4%。由此可见，通过优化循环计算本网壳结构杆件用钢指标有明显减小，达到了优化的目的。

表2 设计变量优化前后对照

表3 设计变量、目标函数优化前后对照

应力比既能反映杆件强度的利用程度，同时也反映了结构的安全储备。图7 为优化前后杆件应力比变化直方图。可以看出，应力比为0.1 和0.2的杆件数量有明显减小，应力比在0.3～0.7 之间的杆件数量有明显增加，这表明优化后网壳杆件强度得到了更加充分地发挥，有利于节省用钢量。

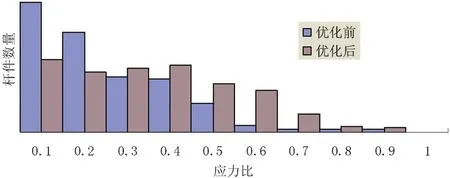
图7 优化前后杆件应力分布比较

表4 为优化后各设计变量与约束变量值。为验证ANSYS 优化程序的杆件稳定分析结果，将优化后的杆件截面定义到原模型，然后按照原工程荷载条件进行静力计算，得到各代号杆件截面类型中最大压应力绝对值σ（见表4），根据表4 中各杆件截面尺寸计算出λ值，再计算出稳定系数值φ，最后计算轴心压杆稳定允许应力σj。计算结果列于表4 中，各截面压杆最大应力均在允许稳定强度范围之内，同时杆件的局部稳定条件β最大值为18.6，小于限值100；网壳最大挠度为62.4 mm，未超过允许挠度限值217 mm。由此可以证实，ANSYS优化结果能够满足网壳结构的压杆稳定要求、长细比要求和杆件局部稳定要求，是一种能够得到满意结果的优化工具，优化结果有效可信。

表4 与优化结果相应的设计变量和约束变量

4 开孔双层球面网壳优化设计的影响因素分析

利用ANSYS 参数化设计语言（APDL）进行编程，保持网壳跨度不变，以结构用钢指标为目标函数，分别以网壳矢高、厚度和杆件截面为设计变量，优化过程中约束条件和作用荷载同前，进行优化设计并分析各因素对用钢指标的影响。

4.1 杆件截面对目标函数的影响

表5 和表6 是优化前后杆件截面面积和用钢指标情况。与原网壳结构相比较，杆件外径有明显减小，杆件壁厚有明显增大。在表6 中可以看到，与整体优化结果相类似，优化后1 ～4 号和8 号杆件截面面积明显减小，5 ～7 号杆件截面呈现增大的情况。优化后网壳用钢指标为43.3 kg/m2，约为原网壳工程的80.9%，节省钢材19.1%。优化后网壳挠度为61.3 mm，满足最大挠度要求。

表5 设计变量优化前后对照

表6 设计变量、目标函数优化前后对照

表7 为优化后各设计变量与约束变量值。表中列出了优化后各杆件编号对应的杆件截面尺寸，将优化后的杆件截面定义到原模型进行静力计算，得到各代号杆件截面类型中最大压应力绝对值σ（见表7），根据表7 中各杆件截面尺寸依次计算出λ值、稳定系数φ和轴心压杆稳定允许应力σj。计算结果见表7，各截面压杆最大应力均在允许强度范围之内，再次说明ANSYS 优化结构能够满足杆件稳定性要求。

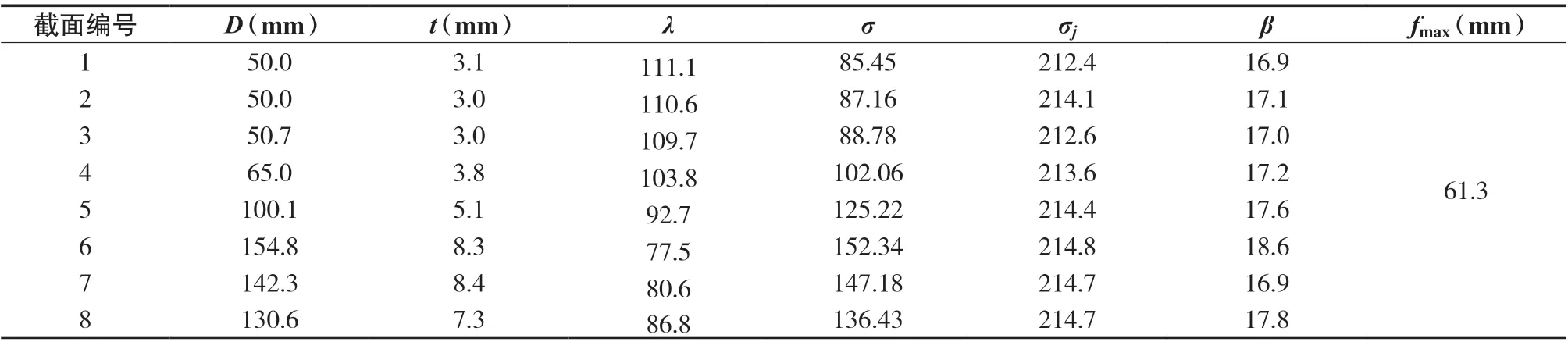
表7 与优化结果相应的设计变量和约束变量

4.2 网壳矢高对目标函数的影响

保持网壳跨度L、厚度h、荷载组合不变，设置一组网壳矢高（见表8），取网壳杆件截面参数为设计变量，对不同矢高的网壳结构分别进行优化计算出目标函数值（见表8），并根据表8 的优化计算结果绘制矢高对用钢量的关系曲线图，见图8 所示。

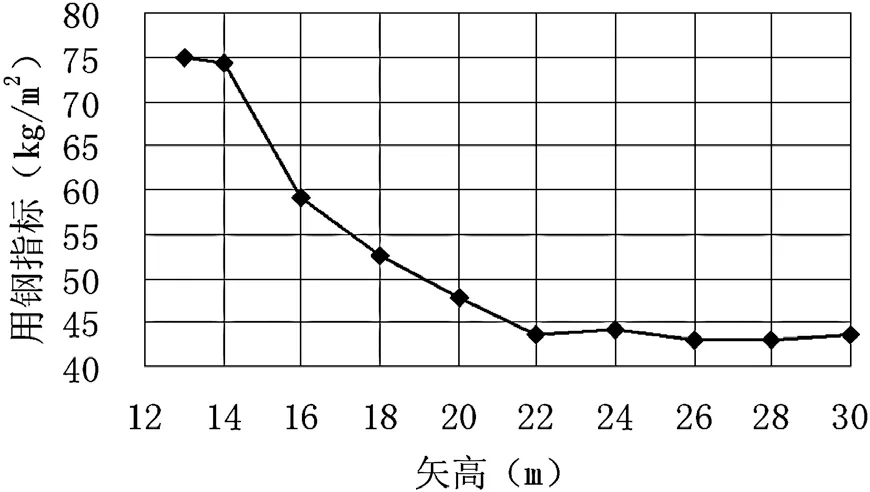
图8 不同矢高与对应用钢指标关系曲线

表8 不同矢高下网壳各约束变量值及用钢指标

由表8 可知，当网壳矢高为28 m 时，得到的目标函数值最小，此时用钢指标为42.9 kg/m2，约为原网壳工程的80.2%，节省钢材19.8%。由图8 可 以 看 出，当13 m ＜F ≤22 m 时，随 着网壳矢高增大，用钢指标呈现出明显减小；当22 m ＜F ≤30 m 时，网壳用钢指标基本保持不变，在43.5 kg/m2左右波动。由此可以得出结论：在网壳网格划分形式、跨度、荷载保持不变的情况下，矢高22 m 为临界值，即当矢高小于22 m 时，网壳杆件用钢指标随着矢高增加而减小；当22 m＜F≤30 m 矢高时，网壳杆件用钢指标基本不变。

4.3 网壳厚度对目标函数的影响

保持网壳跨度L、矢高F、荷载不变，设置一组网壳厚度（见表9），取杆件截面参数为设计变量，分别对不同厚度网壳模型进行优化计算出目标函数值，并根据表9 的优化计算结果绘制网壳厚度对用钢量的关系曲线图，见图9 所示。

由表9 可知，当网壳厚度为1.5 m 时，即规范要求的最小厚度，该网壳结构优化目标函数最小，为38.9 kg/m2，约为原网壳工程的72.7%，节省钢材27.3%。由图9 可以看出，当网壳厚度1.5 m＜h ≤2.1 m 时，随着网壳厚度的增大，结构用钢指标有一定程度增加，但是增加速度比较缓慢，增长范围在38.9～39.9 kg/m2之间。当网壳厚度2.1 m＜h ≤2.9 m 时，杆件用钢指标有较明显增加，增长范围在39.9～41.1 kg/m2之间。由此可以得出结论：在网壳网格划分形式、跨度、矢高、荷载保持不变的情况下，随着网壳厚度的增大，网壳杆件用钢指标呈递增趋势，当网壳厚度大于2.1 m 时，用钢指标增加迅速。

表9 不同厚度下网壳各约束变量值及用钢指标

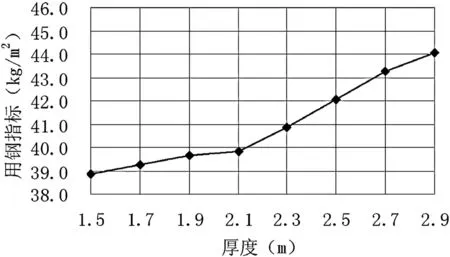
图9 网壳厚度对网壳用钢指标的影响

4.4 荷载对双层球面网壳用钢指标的影响

保持网壳网格划分形式、跨度L、矢高F、厚度h 不变，设置一组荷载值（见表10），均满跨布置，取杆件截面尺寸为设计变量，分别对不同荷载大小作用下网壳模型进行优化计算出目标函数值（见表10），并根据表10 的优化计算结果绘制荷载对网壳用钢量的关系曲线图，见图10 所示。

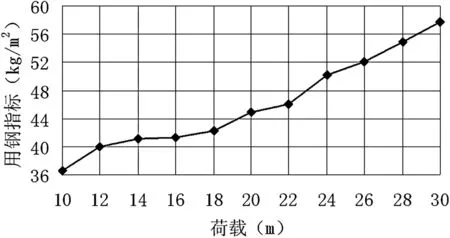
图10 外荷载对网壳用钢指标的影响

表10 不同荷载作用下网壳各约束变量值及用钢指标

由图10 可以看出，随着网壳作用荷载增大，杆件用钢指标逐渐递增，且增长速度均匀，采用直线公式拟合，得下式：

式中C 为用钢指标，x 为荷载大小，在表10 中各荷载作用下，拟合值及误差值见表11。

表11 公式拟合值及误差

由表11 可知，对于本网壳结构，在网壳网格划分形式、跨度、矢高、荷载保持不变的情况下，随着荷载值增加，其用钢指标基本呈线性递增变化。

5 结语

通过对开孔洞双层球面网壳进行结构优化并深入分析网壳矢高、厚度和杆件截面对用钢指标的影响，得出以下结论：

（1）进行结构优化后，网壳用钢指标明显降低，约为原网壳结构的71.6%，节省钢材28.4%，并对优化结果进行稳定承载验算，优化后的网壳整体稳定性及局部稳定性均满足要求。

（2）当网壳矢高13 m ＜F ≤22 m 时，随着网壳矢高增大，用钢指标明显减小；网壳矢高22 m＜F ≤30 m 时，网壳用钢指标基本保持不变。

（3）当网壳厚度1.5 m ＜h ≤2.1 m 时，随着网壳厚度增大，用钢指标增加速度比较缓慢；当网壳厚度2.1 m ＜h ≤2.9 m 时，杆件用钢指标有较明显增加。

（4）在满跨均布荷载作用下，随着荷载的增大，本网壳结构用钢指标明显增加，二者基本呈线性关系变化，采用线性公式进行拟合，结果比较理想。

（5）比较目标函数的各影响因素，本网壳结构用钢指标对网壳厚度变化最为敏感，杆件截面面积变化的影响次之，矢高变化对结构用钢指标影响最小。