安徽省县域粮食产量及生产投入要素的空间差异分析

刘 斌，张华琼

（安徽建筑大学 数理学院，安徽 合肥 230601）

民以食为天，保护和提高粮食产量是我国农业发展过程中面临的长期艰巨任务。粮食问题涉及国计民生，关系到国家粮食安全和经济社会的健康发展[1-2]。影响粮食生产的因素多且复杂，由于不同地区的地理条件和发展水平存在差异，粮食产量和其影响因素具有显著的空间变异性[3-5]。了解粮食生产区域格局及影响因素对于制定合理的粮食生产政策和贸易政策有重要的意义[6]。

粮食生产和布局问题一直是国内学术界关注的热点领域。周立青等人采用空间自相关和多元回归模型等方法，探讨了黑龙江省粮食生产的时空动态及其主要影响因素[7]。杨宗辉等人采用空间自相关分析和空间杜宾模型分析了我国省域粮食生产格局变动的影响因素，得出有效灌溉面积、化肥施用量、粮食播种面积及人均耕地面积均对我国粮食产量有显著正效应的结论[8]。胡慧芝等人采用探索性空间数据分析、重心转移模型和空间误差模型研究了长江流域粮食生产的时空格局演变特征及影响因素，结果表明粮食播种面积和农业化肥施用量对粮食生产均具有显著的正向效益[9]。这些研究揭示了区域粮食生产格局的演变特征及影响因素，为优化粮食生产布局及制定粮食生产政策提供了科学依据。然而，现有的研究往往忽视了地理空间要素对粮食生产的影响，鲜有针对粮食产量及生产投入要素的空间差异分析。

县域是我国最基本的行政单元，是粮食生产发展的重点[10]。本文以2017 年安徽省58 个县和县级市的粮食产量及影响因素为研究对象，在全局回归分析的基础上，采用空间自相关和地理加权回归分析，对安徽省县域粮食产量及其生产投入要素的空间分布差异进行探索，以期对安徽省的粮食生产的政策制定提供参考。

1 研究区域、数据来源和研究方法

1.1 研究区域

安徽省位于中国华东长江三角洲地区，常年农作物种植面积超过8.67×104km2，其中粮食作物面积占75%以上。地势有平原、丘陵、山地等类型，全省有淮北平原、江淮波状平原、皖西山地、沿江丘陵平原和皖南山地5 个地貌区（图1），地跨淮河、长江、新安江三大水系[11]。安徽省处于中纬度地区，四季分明，全省年平均气温在14～17 ℃之间，平均日照1 800～2 500 h，平均无霜期200～250 天，平均降水量800～1 800 mm，农业气候条件适宜，农业资源丰富，是典型的农业大省[12]。

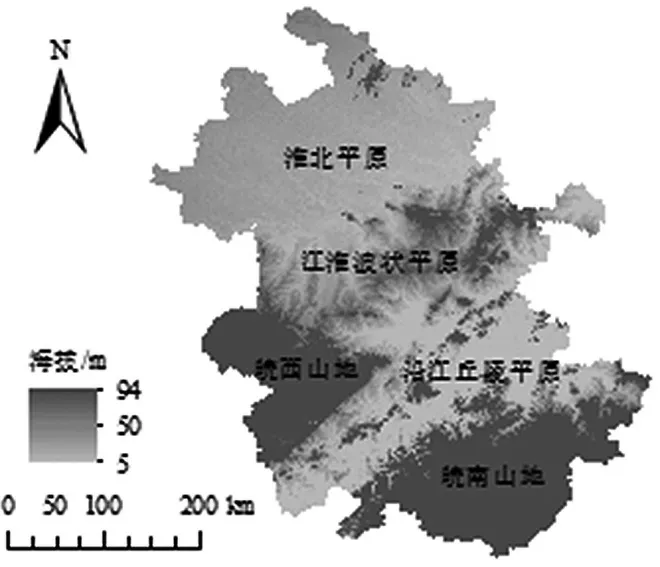
图1 安徽省地貌分区图

1.2 数据来源及处理

考虑到数据的可得性和完整性，本文研究的样本空间单元为安徽省下辖的58 个县和县级市（歙县、和县和宁国市由于数据不全未包括在内），自变量为农业机械总动力（kW）、有效灌溉面积（khm2）和粮食作物面积（khm2），因变量为粮食产量（104t）。数据资料来源于2018 年《安徽省统计年鉴》以及各市县2017 年的《国民经济和社会发展统计公报》。

1.3 研究方法

1.3.1 空间自相关分析

空间自相关分析是用空间距离的函数来度量给定变量的样本之间的相似性、描述样本在区域内分布的空间特征的方法[13]。Moran’s I 指数是空间自相关性分析中最常用的指数，其计算公式如下：

其中N 是空间单元样本的数量，xi和xj是空间单元i 和j 的属性值，wij是i 和j 之间的空间权重是N个空间单元的属性值的平均值。Moran’s I 的取值范围为[-1，1]，I 值为正且越接近1，表明空间单元的正相关性越强；I 值为负且越接近-1，表明空间单元的负相关性越强；I 值越接近于0，表明样本单元的空间自相关性越低。

1.3.2 GWR 模型

通常的全局回归模型由于不考虑地理位置的信息，只表示在平均意义下因变量和自变量之间的相关关系，因此不能反映出回归参数的空间特征。设Y 为因变量，X1，X1，…，XP为自变量，（Yi，Xi1，…，Xip），i=1，2，…，n 是n 组观测数据，则一般线性回归模型的样本形式可表示为：

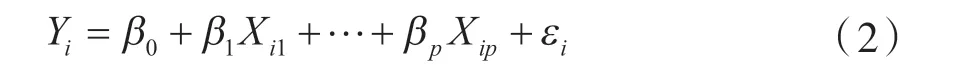
其中β0，β1，…，βp为未知的常值参数，εi为随机误差项，满 足E（εi）=0，Var（εi）=σ2＞0，Cov（εi，εj）=0，i ≠j。对于式（2）中未知参数的估计一般选用普通最小二乘（简称OLS）估计。

地理加权回归（简称GWR）模型作为一种局部回归的技术，将数据的空间位置属性纳入回归模型中，利用回归系数函数在各空间位置处的估计值，分析回归关系随空间位置变化的特征[14]。GWR 模型将一般线性回归模型改写为如下形式：

其中Var（εi）=σ2，βj（u，v），j=0，1，2，…，p 为空间地理位置（u，v）的未知函数；εi（j=1，2，…，n）为独立同分布的误差项且E（εi）=0，对于式（3）中的参数可以通过求解下列矩阵方程来估计：

2 结果

2.1 OLS 模型结果及分析

以粮食产量为因变量，农业机械总动力、有效灌溉面积和粮食作物面积为自变量，运用OLS 方法进行回归分析，其估计结果在表1 中列出。表中VIF 为方差膨胀因子，是用来度量自变量之间相关程度的指标，VIF 越大，表示共线性越严重。R2a 为自由度调整的复决定系数；AICC是模型性能的一种度量，如果两个模型的AICC值相差大于3，具有较低的AICC值的模型被视为更佳模型[14]。由表1可知，模型的拟合优度达到98.4%，各个自变量以及模型整体均通过了5%水平的显著性检验。每个自变量的VIF 均不大于7，模型中不存在严重的多重共线性。通过比较表1 中各自变量的系数可知，粮食作物面积对粮食产量的影响最大，其次为有效灌溉面积，而农业机械总动力对粮食产量的作用较弱。

表1 OLS 模型参数估计及检验结果

通过GeoDa 软件对粮食产量数据进行全局空间自相关分析可得，Moran’s I=0.488，p 值为0.001，表明粮食产量的Moran’s I 指数在1%水平上显著为正，安徽省县域粮食产量的空间分布具有显著的正相关性。

为了全面分析安徽省县域粮食产量的空间差异特征，以粮食产量为横轴，粮食产量的空间滞后向量为纵轴绘制的Moran 散点图，如图2 所示。Moran 散点图由四个象限构成：分布在第一象限和第三象限的点为空间正自相关的点数据，分别表示某地区与其相邻地区皆有较高（低）的粮食产量，说明区域具有集聚性；分布在第二象限和第四象限的点为空间负自相关的点数据，分别表示粮食产量较低（高）的地区，其相邻地区的粮食产量却较高（低），说明区域具有异质性。如果分布在四个象限的点的个数是均匀的，则说明地区之间不存在空间自相关性。

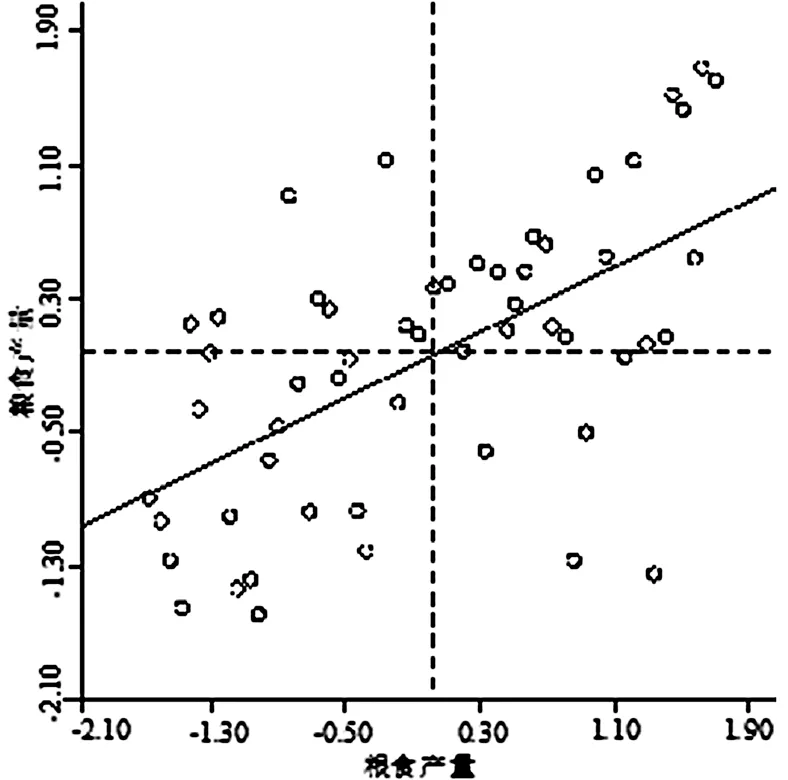
图2 粮食产量的Moran’s I 散点图

根据图2 显示，分布在第一、三象限的点明显多于分布在第二、四象限的点，说明多数县呈现出明显的空间聚集特征。安徽省县域粮食产量的空间分布特征为：粮食产量高的县趋于与粮食产量高的县相邻，粮食产量低的县趋于与粮食产量低的县相邻。进一步对残差进行空间自相关检验，得到Moran’s I=0.45，p 值为0.001，说明该OLS 模型的回归残差并不是随机分布，在空间上存在自相关性。

根据以上分析，安徽省县域粮食产量及OLS模型的估计残差皆存在空间相关性。但是，由于全局回归不考虑地理位置的信息，只表征了在平均意义下因变量和自变量的相关关系，不能反映安徽省县域粮食产量在空间上的非平稳性，为此接下来采用GWR 模型引入空间位置信息以提高模型精度。

2.2 GWR 模型结果及分析

2.2.1 模型构建

为了分析回归关系随空间位置变化的特征，本文采用GWR 方法，以安徽省县域粮食产量为因变量，农业机械总动力、有效灌溉面积和粮食作物面积为自变量，将数据的空间位置属性纳入回归模型中，有效挖掘回归关系的局部特征。表2 列出了GWR 模型的参数估计及检验结果。

根据表2 显示的结果，GWR 模型的拟合优度达到99.4%，AICC 为375.1748，其模型性能较OLS模型有显著提高。表3 给出了GWR 模型的描述性统计结果，表中包括了各自变量回归系数的最小值、上四分位数、中位数、下四分位数和最大值。进一步对模型中的每个参数进行显著性检验，均有p值＜0.001，这表明粮食产量与各变量的关系在空间上是非平稳的。

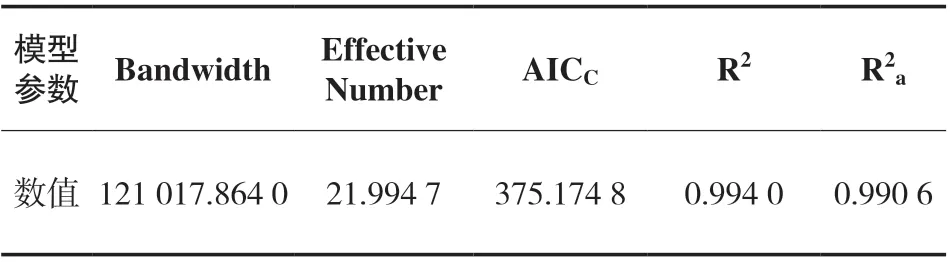
表2 GWR 模型参数估计及检验结果

由于农业机械总动力、有效灌溉面积和粮食作物面积对粮食产量的影响存在空间差异性，因此，根据两种模型的估计结果得出的结论不完全一致。具体来看，根据表1 中OLS 模型的估计结果，农业机械总动力（-0.000 009）对粮食产量有负向影响，有效灌溉面积（0.088 134）对粮食产量有正向影响，而表3 中农业机械总动力和有效灌溉面积的GWR 估计值均有正有负，且绝对值有大有小。以上说明这两个变量对粮食产量的影响方向和程度在不同地区表现不一样，而平均意义上的正向或者负向影响无法体现地区间的差异性。无论是OLS模型还是GWR 模型，在三个自变量中，粮食作物面积对粮食产量的影响皆为最大，且回归系数均为正值，说明其在各地区对粮食产量的影响方向一致。对比粮食作物面积的GWR 估计值和OLS 估计值可知，其GWR 估计值的四分位数范围大于OLS 估计值的±1 倍标准差范围（5.709 617～6.139 733），说明粮食作物面积对粮食产量的影响程度存在较大的空间差异性。

表3 GWR 模型回归系数的描述性统计

从GWR 模型的标准化残差分布图（图3）可以看出，仅1 个县的回归标准化残差落在了2.5 倍标准差外。进一步对残差进行空间自相关检验，得到Moran’s I=0.085，p 值为0.368，未能通过1%的显著性检验，即残差在空间上是随机分布的，这说明GWR 是一种能有效处理回归分析中空间非平稳性问题的技术。

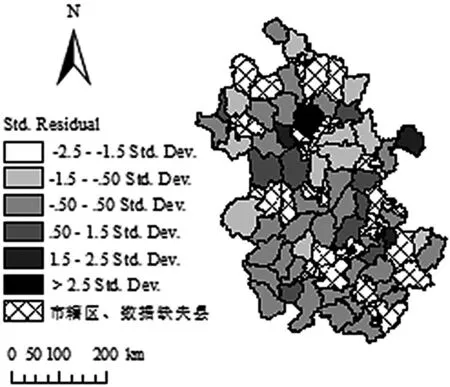
图3 GWR 模型标准化残差的空间分布

2.2.2 结果分析

由于GWR 模型的估计参数因地区而异，本文通过每个变量系数的空间分布图进一步解释单个参数的空间非平稳性特征。

（1）农业机械总动力对粮食产量影响的空间变异特征

从图4 的空间分布来看，农业机械总动力对粮食产量的效应有正有负，回归系数总体上从西南向东北递减。农业机械总动力对粮食产量为正效应的地区主要分布在安徽省的山地和丘陵地域，充分显示了这些区域的农业机械化还有一定的发展空间。这是由于山地和丘陵地区的耕地较分散，耕地形状大小不一且大多根据地势而建，其农业机械化水平的发展受限。由于自然条件的限制，山地和丘陵区域的农业机械化发展水平要落后于平原区域。因此，在这些区域加大农机化的扶持政策，扩大农机化的投入，提升农机化水平，是提高粮食产量的重要手段。农业机械总动力对粮食产量呈负效应的地区主要分布在安徽省的平原区，说明平原区的农业机械化水平较高，处于相对饱和状态。

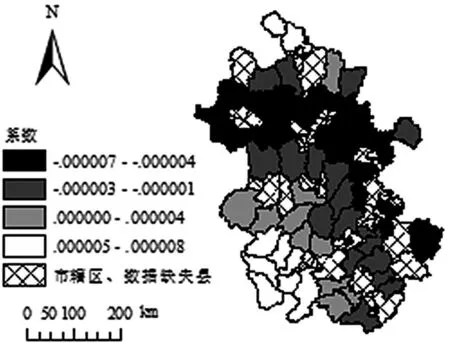
图4 农业机械总动力回归系数的空间分布

（2）有效灌溉面积对粮食产量影响的空间变异特征

从图5 可以看出，有效灌溉面积的回归系数由西部向东北和东南两个方向呈逐渐递减趋势，正值主要见于安徽省的江淮波状平原、皖西山地、淮北平原中南部和沿江丘陵平原；而负值则主要分布在淮北平原的东部及北部和皖南山地。从地理位置上看，淮北平原中南部和沿江丘陵平原除降水直接利用外，粮食作物还得到地下水的补给，因此这些区域的粮食生产对水利灌溉的依赖程度比较小；江淮波状平原和皖西山地水资源较为紧张，自然降水一般难以满足作物的需求，因此粮食生产对补充灌溉的依赖比较高，加之这些区域的水利工程还不完善，有效灌溉面积对粮食产量有显著的正影响。江淮波状平原和皖西山地对农业灌溉的依赖程度比较高，有效灌溉面积的提高对粮食产量的影响最为明显，这些地区应当加大农田水利工程投入，完善灌溉工程的建设。

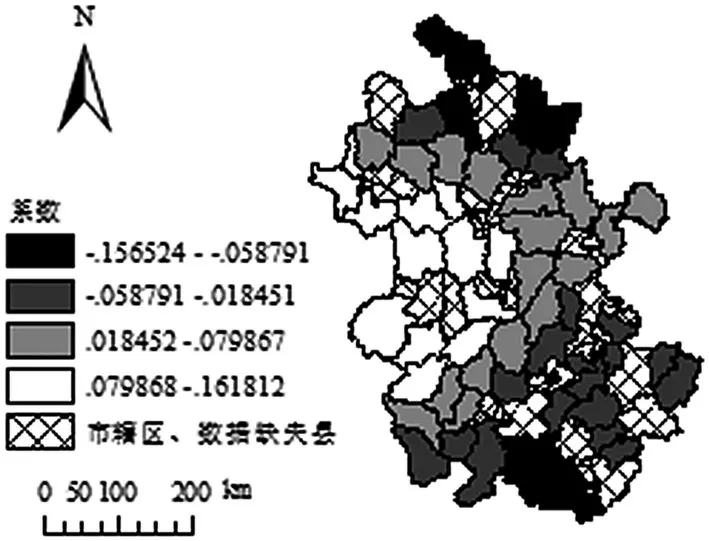
图5 有效灌溉面积回归系数的空间分布

（3）粮食作物面积对粮食产量影响的空间变异特征

根据图6 可知，研究区域内的粮食作物面积对粮食产量的影响皆为正向，总体空间效应呈现出由安徽省西部向东北和东南两个方向递增的态势。在农业机械总动力、有效灌溉面积和粮食作物面积中，仅粮食作物面积的回归系数在所有区域中皆为正值，且回归系数的值普遍较高，这说明粮食作物面积是影响粮食产量的最主要因素，扩大粮食作物的种植面积能显著提高粮食产量。从回归系数的空间分布来看，粮食作物面积对粮食产量影响较大的区域主要位于沿江丘陵平原和皖南山地，粮食作物面积对粮食产量影响较小的区域主要分布在安徽省西部地区。

图6 粮食作物面积回归系数的空间分布

3 结论和讨论

安徽省县域粮食产量存在显著的空间正相关性，在空间上表现出明显的聚集特征：粮食产量高的县趋于与粮食产量高的县相邻，粮食产量低的县趋于与粮食产量低的县相邻。在县域粮食产量与生产投入要素的回归分析中，GWR 模型较OLS 模型在性能上有明显提升，GWR 可以有效地处理回归关系的空间非平稳性问题。在安徽省各区域，粮食作物面积始终是影响粮食产量的最主要因素，保障粮食的种植面积是促进安徽省粮食生产持续发展的重要途径。山地和丘陵区域主要受农业机械总动力的正向影响，在这些区域加大农机化投入，提升农机化水平，可进一步提高粮食产量。江淮波状平原和皖西山地受有效灌溉面积的正向影响，这些地区应当重视农业水利的建设，提高有效灌溉面积。

本文的回归分析仅考虑了空间因素，而粮食产量与其影响因素同样也受到时间因素的影响，因此，用GWR 方法得出的分析结果还有局限性。另外，虽然GWR 模型性能优于OLS 模型，但仍存在一些不足之处，比如它假定所有的变量都具有空间非平稳性，而实际中可能会出现部分变量不受空间位置影响的情况。未来的研究可以把空间和时间因素都纳入回归模型中，改变变量或增加变量的多样性，以期得到更加客观科学的分析结果。