基于遗传算法的潜器压载敷设优化方法
唐波,杨坤,周海波,周生俊,杨振锦
1 武汉第二船舶设计研究所,湖北 武汉 430205
2 中国人民解放军 92578 部队,北京 100161
0 引 言
船舶的初横稳性高是衡量其稳性的重要指标,也是保证船舶正常航行的必要航海性能[1-3]。而潜器作为一类特殊的船舶更是如此,需要同时考虑水面和水下状态的初横稳性高。此外,初横稳性高的裕度还直接决定了潜器服役后可进行现代化改换装的能力。在完成潜器总体布置和各类载荷的统计后,一般通过敷设固定压载(常用压载铁[4])来平衡固定浮容积与各类载荷间的重量差和重量矩差,并控制初横稳性高。因此,压载的敷设方案将对潜器的初横稳性高产生重要影响。
传统的压载敷设方法是:首先根据固定浮容积与各类载荷间的差值计算出需敷设的压载量,随后根据各舱舷间总体布置情况,通过人为的统筹分配,在重量、纵向和横向重量矩基本平衡的前提下,将压载尽可能低位敷设。采用该方法存在的问题:一是工作繁琐,人工迭代工作量巨大;二是难以保证敷设后垂向重心高度最优或是较优。特别是在压载量大、潜器纵向尺寸长、可敷设肋位多的情况下,上述问题将更加突出。因此,研究满足压载敷设需求且总体重心较低的优化方法十分有必要。
现行标准[5]和工程参考书目规定了固定压载总量的计算方法,以及试潜定重后调整的要求,同时还提出了将压载尽量敷设于龙骨底部附近,压载重心纵向位置应位于船舯前后1/6 艇长范围内等原则要求,却未提出全船固定压载敷设的具体方法与指导方针。陈静等[6]研究了优化算法在船舶压载水置换方案中的应用,但压载水置换的目的(主要为环保)及其数学建模、优化目标等与潜器的固定压载敷设完全不同,属于不同领域的问题。黄文华等[7]提出了采用压载铅代替压载铁的技术方向,即利用铅与铸铁的密度差来缩小同质量压载的体积需求,以获得更好的初横稳性高,但选用密度更大的压载铅距离将其广泛应用于潜器还存在一些实际困难,如防腐涂层设计、铅的毒性影响等,且其对稳性高的具体贡献也有待详细计算。当然,无论是选用何种材料的固定压载,工程上迫切需求的仍是一种指导性的方法,即通过优化压载布置来得到重心较低的敷设方案。而在该方面,国内外尚无相关的文献资料,在目前的工程实践中,潜器的固定压载敷设仍然是依靠大量的人工迭代来获得。
为此,本文将首先研究潜器固定压载敷设的横剖面特征,构建潜器压载敷设的数学模型,提取压载敷设的目标函数和约束函数,随后运用智能优化算法得到优化的敷设方案,最后通过计算不同约束参数算例,验证方法的可行性,以获取一些对工程实际具有重要意义的压载敷设原则来供科研和设计人员参考。
1 计算方法
运用智能优化算法对固定压载进行敷设,其关键技术包括建立固定压载敷设的数学模型以及提取压载敷设的目标函数和约束函数这2 个方面。
1.1 压载敷设优化数学模型
图1 所示为简化的潜器模型,其中x方向为潜器纵向,向艏为正,原点为耐压壳体艏艉长度中心点;z方向为潜器垂向,向上为正,过耐压壳体圆心,原点为轻壳体最低点;y方向为潜器横向,向右舷为正。

图1 典型双壳体潜器压载敷设简化模型Fig. 1 Typical simplified model of a double-hull submersible with kentledge
在敷设压载前,潜器的固定浮容积为V0,固定浮容积产生的纵向力矩为MVX, 横向力矩为MVY,垂向力矩为MVZ。除压载外,其他各类载荷产生的重量为W0,对应产生的纵向力矩为MX,横向力矩为MY,垂向力矩为MZ。可供敷设的压载共有N个档位,其中第i个档位敷设的压载重量为Wi(空气中重),此档位置处压载合计的重心为纵向Xi,横向Yi,垂向Zi。压载敷设应满足的约束条件包括重量、纵向力矩和垂向力矩3 个方面。在重量上,压载应平衡固定浮容积与其他载荷的差值:

在纵向上,压载应平衡固定浮容积与其他载荷产生的纵向力矩的差值:

在横向上,压载应平衡固定浮容积与其他载荷产生的横向力矩的差值:

式(1)~式(3)为约束函数,其中 ρYZT为压载密度, ξW,ξX,ξY均为一小值。水下初横稳性高h[8]为

式中:r为横稳心半径;c为自由液面修正系数。考虑到敷设压载后压载整体对潜器的浮心和重心均会产生一定的影响,为简化问题,将目标函数简化为压载总体重心最低,即目标函数可以写作

为求得每一档位的重量值Wi和 重心高度Zi,需对压载敷设进行数学简化。每档可敷设压载位置的横剖面如图2(a)和图3(a)所示,即压载的各层累积填充于底部或舷间下部区域。通过类比,每一块压载相当于有限元法中的“六面体单元”,由于这些“单元”尺寸小,且实际间隙可忽略不计,采用逆向思考,可将这些离散的“单元”压载组合看做一个连续的整体或液体,“充满”了可敷设区域。

图2 典型双壳体潜器舷间敷设压载简化模型1Fig. 2 Typical simplified model-1 of a double-hull submersible with kentledge

图3 典型双壳体潜器舷间敷设压载简化模型2Fig. 3 Typical simplified model-2 of a double-hull submersible with kentledge
压载的上边缘亦有多种情形,需讨论后进行简化。图4 所示为2 种情况下的上边缘,其中图4(a)情形下压载的合计重心高度为G1,图4(b)情形下压载的合计重心高度为G2,考虑到“液体总是在最低势能处静止”, 因此,在体积V相同的前提下,图4(a)中重心G1较 图4(b)中重心G2更低。实际上,图4(a)所示顶部水平的情形为重心最低的唯一情形,后续将在简化模型中采用此上边缘形式进行计算。

图4 两种舷间敷设压载形式的高度差别Fig. 4 Gravity center difference of two simplified fixed kentledge models
因此,可将压载敷设情况简化为如图2(b)和图3(b)所示的函数模型。其中,图2(b)为压载边界上限较低,未超过耐压壳体肋骨下边缘的情形;图3(b)为压载边界上限相对较高,超过耐压壳体肋骨下边缘的情形。在图2(b)和图3(b)中,压载敷设边界区域的横坐标可以表示为垂向坐标的函数。对于内边界,在y≥0区 域,设y=F(z),该函数代表耐压壳体外肋骨边界的圆弧线,该圆弧线的半径为R2; 而在y≤0区 域,y=-F(z)。对于轻壳体边界,在y≥0区 域,设y=G(z),该函数代表轻壳体边界的圆弧线,该圆弧线的半径为R1;而在y≤0区 域,y=-G(z)。
根据以上假设,在图2(b)所示简化模型中,压载上边缘与轻壳体在第1 象限交点的横坐标可以表示为Yi0=G(Zi0);在图3(b)所示简化模型中,压载上边缘与耐压壳体肋骨、轻壳体在第1 象限交点的横坐标可以表示为Yi0=F(Zi0),Yi1=G(Zi0)。
针对图2(b)中压载部分,其截面积为

对应的重心高度为

针对图3(b)中压载部分,其截面积为

对应的重心高度为

在特殊情况下,若因总体布置等限制,导致压载在左右舷不对称敷设(图5),则其在左舷的面积和重心高度分别为:

图5 典型双壳体潜器舷间敷设压载简化模型3Fig. 5 Typical simplified model-3 of a double-hull submersible with kentledge
同时,还需要考虑左舷重心横向位置:

在右舷,对应的结果分别为:


则敷设此档位处压载所产生的重量值为:
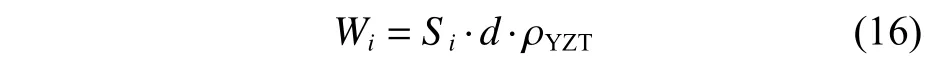
式中,d为此档位处压载在纵向上的长度尺寸。
1.2 遗传算法
如上节所述,每档位处压载的重量和重心高度并非为连续函数,且考虑到压载敷设的档位较多,拟采用遗传算法来作为寻优的优化算法。遗传算法于1962 年由John Holland 提出,算法中引进了群体、适应值、选择、变异、交叉等基本概念,以应用于函数优化,主要具备以下优点[9]:
1) 遗传算法以参数的编码集作为运算对象,其在搜索的过程中不受优化函数连续性及其导数求解的限制,因而具有很强的通用性;
2) 遗传算法直接使用由目标函数确定的适应度函数信息,以群体为单位执行搜索过程,可以较快地搜索到适应度较好的搜索空间,因而具有较强的全局搜索能力。
遗传算法的流程如图6 所示[10]。

图6 遗传算法流程图Fig. 6 The flow chart of genetic algorithm
2 计算方法
2.1 算例模型
首先,为验证基于遗传算法的固体压载敷设优化方法的可行性和普遍适应性,选取了表1 中所示较为宽泛的压载重量、需提供的纵向和横向力矩以及档位数量等参数范围来进行仿真计算。

表1 宽范围算例模型参数表Table 1 The model parameters of examples with wide variation
随后,通过控制变量,研究压载重量、需提供的纵向和横向力矩、档位数量、是否左右对称敷设等不同参数变化对优化结果的影响,然后通过观察每一参数的优化趋势,对实际敷设提出指导性意见。具体的控制变量算例如表2 所示。

表2 控制变量算例模型参数表Table 2 The model parameters of controlling variables for calculation examples
控制遗传算法的主要参数设置参见表3。

表3 遗传算法主要参数设置Table 3 The parameter setting of genetic algorithm
2.2 结果分析
1) 优化方法的可行性分析。
通过构建数学模型,提取目标函数和约束函数,并结合遗传算法进行优化计算,得到表1 中各算例的压载敷设结果如图7 所示。由图可见:

图7 宽范围算例下各档位左右舷压载敷设高度优化结果Fig. 7 The optimization results of kentledge laying height at the left/right side in the calculation examples with wide parameter variation
(1) 在不同压载重量、需提供的纵向和横向力矩,以及档位数量等参数条件下,采用本文所提的建模和遗传优化方法均能得到优化结果,且在不同参数下,优化结果均是以一种“梯度”的趋势去平衡力矩的,证明该方法可行且适用。
(2) 在档位较少的情况下,如算例1,2,3,各档位“梯度”的一致性较好;在档位较多的情况下,如算例4,出现了多处局部不符合一致的“梯度”现象。经分析,档位数的增加即转化为变量数的增加,需同步增加遗传算法中种群的数量才能得到更好的结果,但同样也将增加计算时间。
同时,对表2 中控制变量的各算例进行计算,结果如图8 所示。由图可见,在各参数下均能通过遗传算法得到优化结果。针对每一算例,选取20 次优化计算的最好值进行后续的对比分析。

图8 控制变量各算例优化计算结果对比Fig. 8 Comparison of optimization result of controlling variables for calculation examples
2) 同一算例不同优化结果的原因分析。
如图9 所示,针对算例5 的20 次优化计算结果,选取最好和最差的结果(相当于一般的人工迭代方案)进行对比,研究相同约束条件下压载重心高度的影响因素。由图9(a)可看出,两结果均呈艉部少、艏部多的敷设规律,这样可以平衡给定的纵向力矩(在敷设压载前,潜器艉部较重)。但同时也观察到,较好算例各档位之间梯度较小,压载重心低;而较差算例的梯度则明显较大,导致压载重心较高,较好算例的压载重心比较差算例约低23%。因此,在保证平衡纵向力矩的前提下,为了降低压载重心,应以较小的“梯度”去敷设。3) 敷设档位数量对优化结果的影响分析。

图9 各档位下左右舷较好和较差压载敷设计算结果对比(算例5)Fig. 9 The best and worst left/right side kentledge laying height results comparison of example 5
如图10 所示,选取算例5 和算例6 的最好结果,研究在其他约束相同的条件下,不同敷设档位数量对压载重心高度的影响。其中算例6 的敷设档位较多,共9 档,在进行优化时将压载尽量均摊到了各档位,相较于算例5 共计5 档的敷设结果,其重心高度明显降低。因此,在敷设压载时,为降低压载重心,应敷设尽量多的档位。

图10 左右舷压载敷设档位数量对优化结果的影响Fig. 10 Different amount of laying frames influence on left/right side kentledge laying height optimization
4) 纵向力矩对优化结果的影响分析。
如图11 所示,选取算例5、算例7 和算例8 的最好结果,在其他约束相同的条件下,研究不同平衡纵向力矩对压载重心高度的影响。由图11(a)可以看出,算例7 需要的平衡纵向力矩最小,为10 t·m,算例8 需要的平衡纵向力矩最大,为200 t·m,优化结果为算例7 的重心最低,算例8 的重心最高。通过观察敷设情况,分析造成此差异的原因,认为需要的平衡力矩越大,平衡力矩所产生的各档位的敷设梯度越大,重心也越高。

图11 纵向力矩对各档位左右舷压载敷设优化结果的影响Fig. 11 Different longitudinal moment influence on right/left side kentledge laying height optimization
5) 高度限制对优化结果的影响分析。
如图12 所示,选取算例5 和算例9 的最好结果,在其他约束相同的条件下,研究某档高度限制对压载重心高度的影响。由图12(a)可以看出,对于最靠近艏部的一档,若将其压载敷设高度限制为2 米,结果显示,将会导致其他档位需要采用较大梯度的平衡纵向力矩,致使其重心高度明显高于算例5,如图12(b)所示。可见,如果存在高度约束使固定压载敷设无法形成一致的梯度时,压载重心将相应增加。

图12 高度限制对各档位左右舷压载敷设优化结果的影响Fig. 12 The vertical restriction influence on left/right side kentledge laying height optimization
6) 优化算法平衡横向力矩效果分析。
算例5~算例9 在建模时即限制其为左右舷对称敷设,而算例10 则放开了左右舷敷设高度的限制,通过算法来自行寻找最优解。算例10 需要平衡的横向力矩为0,如图13 所示,故其找寻到的优化解仍为左右舷对称,且其重心也与算例5 基本相当,说明优化算法可以很好地平衡左右舷力矩。7) 横向力矩对优化结果的影响分析。
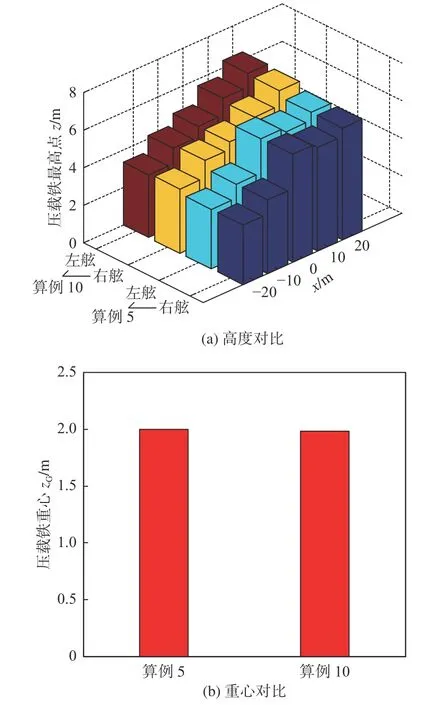
图13 各档位左右舷压载敷设优化算法平衡横向力矩效果Fig. 13 The left/right side kentledge laying height optimization result on lateral moment
如图14 所示,选取算例10、算例11 和算例12的最好结果,在其他约束相同的条件下,研究不同平衡横向力矩对压载重心高度的影响。由图14(a)可以看出,算例10 需要的平衡横向力矩最小,为0 t·m,算例12 需要的平衡横向力矩最大,为100 t·m,优化结果为算例10 的重心最低,算例12的重心最高。通过观察敷设情况,分析造成此差异的原因,认为需要的平衡横向力矩越多,左右舷平衡力矩所产生的各档的敷设梯度越大,重心也就越高。
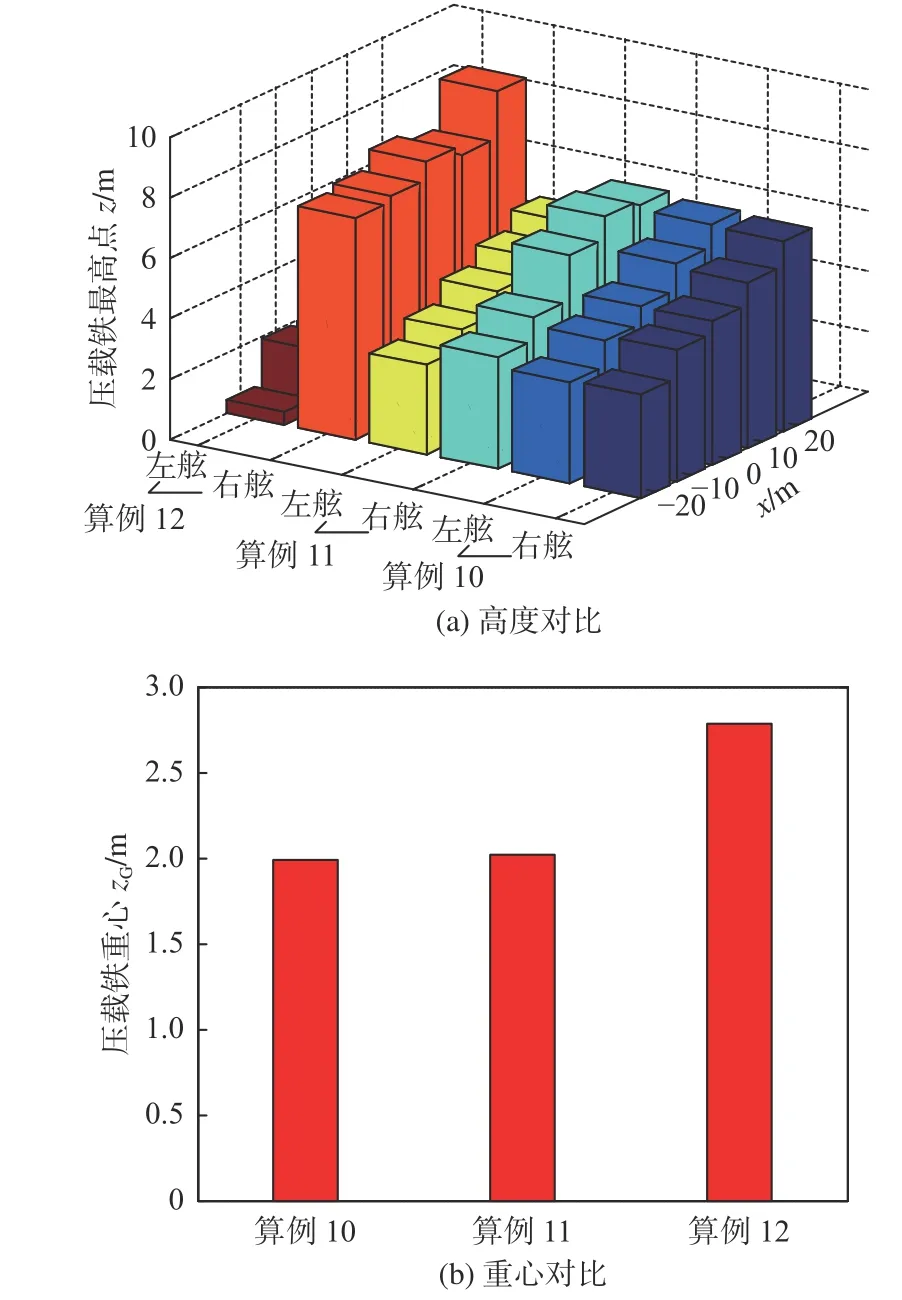
图14 各档位左右舷不同横向力矩压载敷设计算结果对比Fig. 14 Different lateral moment influence on left/right side kentledge laying height optimization
3 关于应用问题的思考与讨论
压载敷设优化方法在实际工程应用中还面临着以下2 个方面的问题:
1) 对于排水量小、纵向长度较短的潜器,以上压载敷设寻优方法可以很好地适用;但对于排水量大、纵向敷设档位可达上百档的潜器,因变量数目显著增加,导致计算仿真将消耗大量的时间。
2) 在潜器设计中,耐压壳体与轻壳体之间的舷间往往存在一些布置区域限制因素,如舷间水道围壁、通海阀围壁等,在建模仿真时需要予以考虑。
3.1 多档位敷设优化问题
针对固体压载可敷设档位多,同步计算资源消耗大的情况,尝试考虑了“先粗分,后细分”的优化模式,即首先根据舱室或舱段划分10 个以内的简化档位,得到第1 轮的重量优化分配后,再对每个舱室纵向范围内的各档肋位进行第2 轮的详细优化分配。
图15 所示为进行第1 轮的粗分和第2 轮细分后的优化结果。在局部“细分”过程中,每一档为了得到最低的重心会进行等分,从而使得在全局上无法得到梯度一致的结果,因此以上方法实际上是一个“误区”。

图15 优化结果示意图Fig. 15 Schematic diagram of the optimization results
综上,针对档位较多的情况,建议仍旧按照每档建模、统一优化的方式进行计算;而对于优化结果可能出现的局部梯度不一致的问题,可根据“最小梯度”经验人为地进行快速调配,以便在消耗尽量少的计算资源的情况下得到优化结果。
3.2 关于布置区域限制因素
针对有布置区域限制的情况,如图16(a)所示,在建模时可以简化为分段函数,简化模型参照图16(b)和图16(c)。实际上,考虑到分段函数导致的建模的复杂性,其仿真将会消耗更多的计算资源,因此建议在实际应用中,在档位较多的情况下可释放这些限制因素,在计算完成后再自行进行人工调配,这样亦能得到工程上可接受的结果。例如对于图16(a)所示情况,可直接先按照如图3(b)所示无布置区域约束的数学模型进行计算,后续再进行调配。

图16 布置区域限制示意图及简化模型Fig. 16 The area restrict sketch and simplified mathematic model
4 结 语
本文基于一种离散模型连续化的逆向思维,对潜器固体压载敷设进行数学建模,然后提取约束函数和目标函数并结合遗传算法对固定压载方案进行了寻优。多个算例证明,本文所提方法可行且有效:在平衡重量、纵向力矩和横向力矩的前提下,无需人工干预,即可寻找出重心较低的压载敷设优化方案,得到的较好算例相比较差算例(相当于人工算例)其重心下降近23%,大幅降低了人工迭代的工作量。同时,本文对不同参数条件下优化结果的分析研究,以及有关及实际应用问题的思考与讨论,可供工程设计人员参考。

