装备维修器材仓库选址鲁棒优化模型

王 清, 苏正炼, 严 骏

(陆军工程大学 野战工程学院, 江苏 南京 210007)

在装备维修器材管理中，器材的储存与转运主要借助仓库实现。为了在部队要求的任何地区都能提供所需的军事装备维修器材，应当构建合理的储备布局[1]。装备维修器材仓库的选址决定了后期器材输送的模式与成本，建设耗资巨大，位置不宜随意变动。以往考虑选址因素(如部队分布、建设费用、交通状况、运输距离、运输成本和部队需求等[2])时，为计算方便，均假设为定值。但某些参数的微小扰动可能使原决策由最优解变成次优解或不可行解。因此，不确定参数下的装备维修器材仓库选址问题更加贴近实用，通过建立具有较高抗干扰能力的数学模型，使解在参数摄动时始终具有可行性与优化性，可以为决策者提供更为稳定的决策方案。

文献[3]提出了鲁棒优化解决参数扰动，得到了众多国内外学者广泛关注。文献[4]研究了离散需求情景概率不确定下的多周期库存鲁棒优化模型，验证了所建模型能抑制需求分布不确定对库存绩效的影响。文献[5]考虑了多重覆盖的应急设施协同布局鲁棒优化问题，建立了双目标优化模型，研究了场景内不确定需求和随机场景对设施布局的影响，并验证模型。文献[6]针对2个阶段的应急设施选址建立了鲁棒优化模型，通过与传统P-center模型对比说明了模型的合理性与有效性。文献[7]研究了两个受车辆容量和时间窗限制的鲁棒优化模型，对车辆路线进行了优化，减少了距离和时间。文献[8]考虑了项目调度中的工期不确定，建立的自适应鲁棒优化模型减少了最坏情况下的完工时间。文献[9]在能源供应系统中建立了多目标鲁棒优化模型，利用混合整数线性规划求解，说明了鲁棒优化在能源设计领域的作用。文献[10]针对不确定条件下的指派问题，在目标函数中添加了2个惩罚加权系数来表达决策者对风险的防范程度，实现模型与解的鲁棒性平衡。

目前，鲁棒性主要应用在机器控制、民用供应链等方面，在军事方面的应用较少，基于鲁棒优化的装备维修器材选址模型研究不多，其中的多目标问题研究更少。通过研究不确定参数下的器材仓库选址，不仅可在理论上丰富鲁棒优化理论，而且具有较强的军事效益。根据器材仓库选址的实际情况，本文主要采用情景分析法描述维修器材需求量的不确定性，建立对应的双目标鲁棒优化模型，结合智能算法对问题求解，并研究风险系数对目标函数及其方差的影响。

1 模型建立

1.1 模型描述

结合传统的覆盖问题、中心问题和中位问题[11]，对本文模型进行选址。在固定区域范围内，若干维修基层分队对某型装备维修器材存在需求，而且需求量不确定，但可表示为多种情景的集合，可以从已知需求点中选出建立装备维修器材仓库的位置，实现对所有需求点的器材补给，使得需求为集合中任一情景时，选址方案的特定目标函数值及其波动最小。为准确描述模型，需做以下假设：(1)仓库位置只能从需求点中选出，不得重新另选地址构建，一个需求点只能由一个仓库实施保障；(2)仓库选址的相关费用已知，暂时不受市场影响，为定值；(3)仓库的车辆运输与储备能力能够满足模型需求；(4)各器材需求点位置确定，调度过程不能更改。

1.2 确定模型结构

当需求存在多种情景时，为方便构造鲁棒优化模型，并与鲁棒解结果对比，首先建立需求确定时的装备维修器材仓库选址模型(Definitive model，DM)，以获得各情景下的最佳目标函数值。

定义各参数如下：J为仓库总数量；K为需求点总数量；j为仓库编号，j=1,2,…,J；k为需求点编号，k=1,2,…K；Bj为第j个仓库的固定建设成本；djk为器材仓库j到需求点k的距离；N为拟选仓库位置的总数量；qk为需求点k的维修器材需求量；mk为单位维修器材在需求点k的效用系数；cjk为仓库j向k部队运送的单位数量维修器材单位距离运费；Yjk为第j个器材仓库与第k个需求点之间是否存在供需关系，是则取1，否则取0；Xj为第j个装备需求点位置，若位置为维修器材仓库时取1，否则取0。

模型目标函数包括f1和f2，f1为效用值，f2为总成本值，其表达式分别为

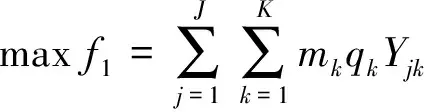
(1)

(2)

根据模型描述，约束条件包括

(3)

(4)

Yjk≤Xj

(5)

Xj∈{0,1}

(6)

Yjk∈{0,1}

(7)

式(1，2)为目标函数，式(3)为一个需求点只能由一个维修器材仓库提供器材保障，式(4)为维修器材仓库的数量要求，式(5)为只有被选择出来的仓库才能与需求点产生供需关系，式(6，7)为决策变量的0、1约束。

1.3 基于鲁棒优化的双目标选址模型

鲁棒优化方法对不确定量的描述一般有区间分析法与情景分析法2种[12]。维修器材需求数量对决策方案的选择具有较大影响，情景集合主要描述日常训练、战时保障、非战争军事行动等场合的需求差别。鲁棒优化中的差异模型引入了风险系数，更便于调节解的优化性与鲁棒性[13]。在DM基础上，建立鲁棒优化模型(Robust optimization model，ROM)。

(8)

(9)

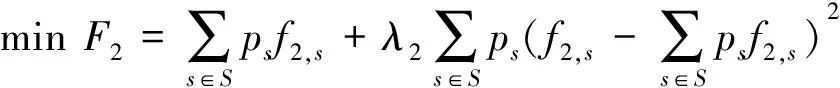
(10)

(11)

ROM的约束条件与DM相同。

在不同的情景下：式(9)将式(1)的最大化效用转化为最小化问题，便于鲁棒模型建立与求解，M为固定值；式(11)为情景s下的建设固定费用与运输费用之和；式(8，10)的F1和F2为鲁棒优化的双目标函数值，分别引入了风险系数λ1和λ2，构成各自风险项，用于决策者权衡模型的鲁棒性与优化性。

2 模型求解

鲁棒优化模型中，式(8，9)为二次项，属于非线性整数规划模型，用精确算法、枚举法与一般商业软件难以求解[14]，本文选用多目标智能算法中的NSGA-Ⅱ对模型进行求解，算法具体步骤为：

(1)染色体编码，构建初始种群P。采用实数编码，从1～K共K个数中不重复地选择N个整数，表示N个仓库点，形成染色体，如K=4，N=20时，染色体2-6-12-18表示选择第2、6、12和18个需求点作为仓库地址。重复执行，直到产生满足数量n的染色体作为初始种群P。

(2)计算各目标值，进行非支配排序。对种群P中的每个个体xi，两两比较对应的所有目标值，若不存在xj的所有目标值均优于xi的目标值(xj≠xi)，则令xi解的秩为ra=1，所有互不支配的xi构成集合Q1。在集合(P-Q1)中，若不存在其他解完全支配解xk，则令xk的秩为ra=2，所有互不支配的xk构成集合Q2。依次进行下去，直到所有个体均被赋予秩值。在同等秩的解中，再按照其拥挤距离[15]排序，拥挤距离大的优先。

(3)遗传操作，生成子代P′。遗传操作包括交叉与变异，与传统遗传算法类似。遗传操作并非对所有父代进行，在产生的初始种群中采用二元锦标赛方式产生交配池规模为t的父代个体，针对这些父代个体实施交叉、变异得到子代P′。

(4)对父代与子代综合P∪P′个体进行非劣排序，计算拥挤距离d。将步骤(3)得到的子代P′与最初的P进行合并，按照步骤(2)的计算方法得到种群的秩与拥挤距离。

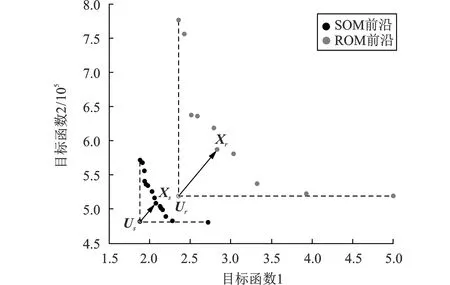
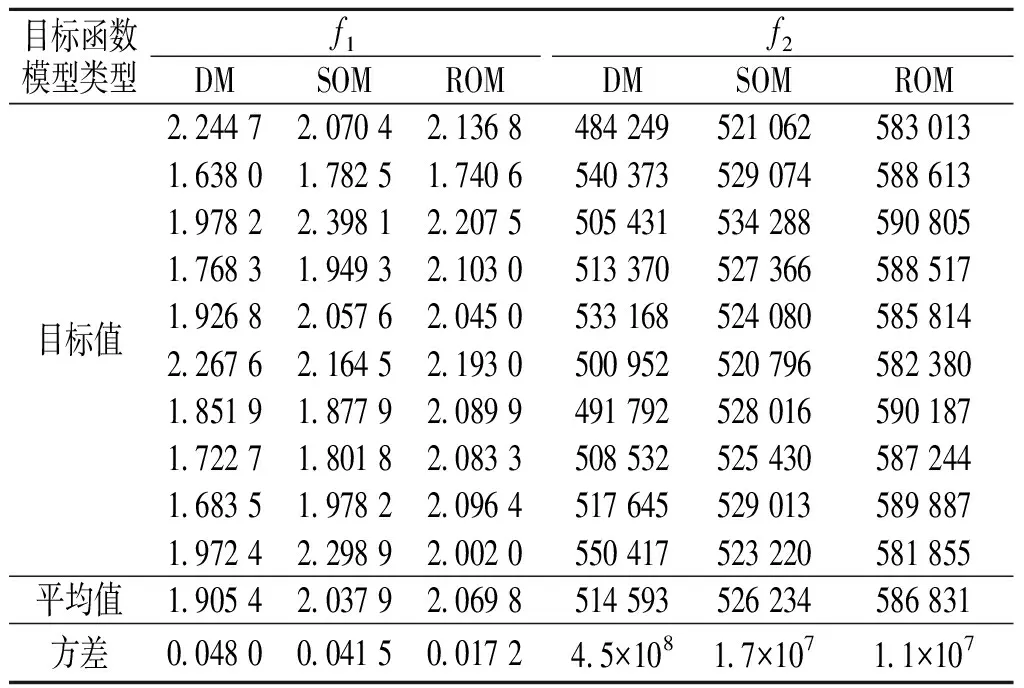
(5)前n个个体精英保留。当ra

(6)解的选取。多目标问题与单目标问题的不同之处在于同时存在多个解，在无特殊说明时无法决定哪个解为最优解。若将每个情景下所有的Pareto解都代入计算，将会造成计算量较大，因此有必要在每个Pareto解集中根据一定规则选择相对较好的解作为最优解。常用做法是从基于多目标之间的均衡性出发，选择解集距离乌托邦点(Utopia point)最近的点作为最佳解输出[16]，如图1所示。具体做法以双目标为例，描述如下：① 在目标空间f1和f2找到Pareto解集的极值点h1和h2，分别沿各自坐标作平行线交于一点，该点即为乌托邦点；② 以乌托邦点为中心，与Pareto解集中距离最近的点作为选取出的最终解向量X。

图1 乌托邦点下的最佳解选取

3 实例验证

3.1 模型实验分析

在600×400区域范围内存在20个装备维修器材需求点，从中选择4个作为仓库，以q1=(58,83,83,55,64,64,47,83,83,64,55,47,54,37,68,74,83,64,92,46)为基准，根据不同需求在±40%随机波动产生q2～q10，共10种情景。

情景出现概率向量p=(0.05,0.05,0.1,0.15,0.15,0.15,0.1,0.15,0.05,0.05)。

固定建设成本B=(102,124,133,112,139,100,138,89,162,129,130,96,104,153,126,116,135,148,127,116)。

按照上述计算过程求解模型。其他参数设置如表1所示。

表1 算法参数设置

表2 各情景下的DM解

为体现鲁棒优化模型的效果，同时利用随机优化方法计算解，剔除2个目标函数中的风险项，仅将期望值作为目标，模型记为SOM。使用NSGA-Ⅱ算法求解ROM与SOM，得到两者的Pareto前沿，如图2所示。其中，SOM选址最佳方案为6-8-2-19，目标值为f1，SOM=2.070 3，f2，SOM=508 792。ROM选址最佳方案为2-13-19-9，目标值分别为f1，ROM=2.827 8，f2，ROM=586 423，模型各选址中心覆盖的需求点如表3所示。

图2 ROM、SOM的pareto前沿

表3 SOM与ROM最优选址方案

图2中，Ur，Us和Xr，Xs分别表示ROM，SOM的乌托邦点与距离该点最近的Pareto解集中的解向量，作为对应模型解。

为验证解的有效性，将SOM和ROM选址方案代入10种情景集合中，分别计算在当前情景下的目标函数值，平均值和方差的结果如表4所示。

表4 DM、SOM和ROM计算结果

对比ROM与SOM解对应的目标函数可以发现，ROM下的平均值2.069 8、586 831均分别大于SOM的2.037 9和526 234，也分别大于DM的1.905 4与514 593，这是控制目标函数的变化程度而添加惩罚项造成的。

从表4的平均值与方差可以看出，确定情景下SOM和ROM目标函数均大于DM模型目标值。ROM在平均值指标上虽然相对较差，但在方差指标上，ROM却占明显优势。目标1的方差为0.017 2，只有DM和SOM的1/2～1/3，目标2的方差为1.1×107，亦小于DM和SOM，说明无论发生何种情况，ROM始终能保证解在2个目标函数的变动范围相对较小，使得选址方案基本可行，避免因需求参数变动出现反复决策。

3.2 风险系数λ分析

在双目标中，引入了2个风险系数λ1和λ2，用以调节模型优化与鲁棒性，在诸多文献中一般只研究单目标时情景分析方法下的风险系数、目标函数和方差关系[17-18]，而对多目标下风险系数的研究较少。基于此，分别设计了2个风险参数变化时对2个目标值和方差的影响实验。

固定λ1=50，λ2从0.001 5以0.001的步长均匀变化到0.010 5，得到f1=3.32，σ1=0.017 2，目标函数f2及方差σ2的结果如图3(a)所示。固定λ2=0.005 5，λ1从10以10的步长均匀变化到100，得到f2=537 773，σ2=1.1×107，目标函数f1及方差σ1结果如图3(b)所示。

图3 λ1、λ2变化时目标函数值与方差的关系

从实验结果可以看出，固定λ1=50时，λ2的变化并未对目标函数f1及方差σ1造成影响，仍然为定值。而从图3(a)可以发现，目标函数f2随着λ2的增加逐步递增，方差σ2相应降低，说明当决策者重视该目标的偏差程度，希望得到更小的方差时，必须付出更大的费用代价。同样的结论在图3(b)中也能得出，当方差σ1越小时，目标函数f1更大。由式(10)进一步可知对应效用值降低，说明稳定需要损失一定的效益值才能获得。但是过分追求方差最小化可能导致目标函数的快速上升，因此必须在可接受的范围内调整各风险系数。

针对2种风险系数λ1和λ2的变化规律，决策者可根据不同的情景采用不同的风险系数值。平时情况下的装备维修器材选址时，主要考虑经济因素，决策者多希望在需求不确定时，总费用投资变化不大，这时主要通过选取合适的λ2获得较为理想的选址方案。而在战争或者紧急救援行动中，多以效益值(如可救助人数、维修保障程度)优先，因此需保证任何情景下的效益值变化最小，这时需要适当增加λ1。2个风险系数的独立取值可使决策者在面对不同需求时具有更加灵活的应对策略。

4 结论

需求量的不确定性是装备维修器材仓库选址中必须考虑的问题，应采取措施保证决策方案的持续有效。本文采用情景分析法描述需求量的变化，在效益与成本的双目标函数中均引入风险系数控制各目标的波动范围，得到了器材仓库选址问题的鲁棒优化模型。MATLAB实验仿真结果表明，相对随机优化而言，鲁棒优化可通过牺牲部分函数值获得更加稳定的鲁棒解。同时，风险系数也有助于决策者根据决策环境灵活制定选址方案。但情景分析法仍然无法很好地表述参数变动规律，由于仍存在一定误差，下一步将集中研究不同参数变化规律下的装备维修器材仓库选址鲁棒优化模型。