一种战时航空弹药需求预测方法

陈 杨， 徐晓双， 赵亮亮， 刘保军

(1.空军工程大学，河南 信阳 464000；2.信阳职业技术学院，河南 信阳 464000)

航空弹药是航空兵作战的机载弹药总称。海湾战争之后，战争消耗量大是世界各国一致的认识，靠主观经验进行航空弹药需求预测的做法已经不能满足未来作战的需求。减少主观因素所带来的缺陷，是当前空军部队航空弹药保障工作中亟待解决的重大问题。目前，对航空弹药的需求预测有数理模型预测、案例推理法、规则推理法、统计学法、微分方程法等，每种方法各有优缺点。统计学和微分方程法难度不高，但是精度同样不高；案例推理法和规则推理法精度适中，时间短，但是处理效率低；数理模型预测具有精度较高、时间短的特点，同时具备一定的通用性，便于移植。本文采用数理模型预测对航空弹药需求进行分析。航空弹药的需求预测分为平时需求预测及战时需求预测。航空弹药的平时需求量可根据历史数据，通过构建合理的模型实现预测；对于战时的需求量，则根据不同的航空弹药种类构建不同的模型进行预测，由需求结构及数量两部分组成。

传统的航空弹药作战需求总量预测是建立在指挥员对以往作战经验总结的基础上，这种方法曾经为作战胜利发挥了重要的作用。但是，随着航空弹药的发展及空战模式的改变，这种方法有很大的局限性，已不能满足未来战争的需求。国外研究方面，文献[1]提出了基于MarKov模型的战时弹药预测，利用3σ准则提取航空弹药供应能力关键指标，组建战时弹药保障评价体系，用遗传算法进化寻优弹药供应保障模型。此模型精度高，但是可扩展性差。文献[2]提出了Bayesian准则的预测模型，该方法依据方差分解和最优线性非齐次预测给出战时航空弹药的需求预测模型。此模型具有可行性，但预测精度低。国内研究方面，文献[3]采用神经网络对航空弹药作战需求进行预测，克服了局部收敛的问题，预测精度较高，达到了全局最优效果。文献[4]基于历史数据构建了航空弹药需求的多元线性回归预测模型，并对模型进行了F检验及t检验。文献[5]分析了航空弹药需求的多元线性回归预测、灰色预测、并联及串联灰色多元回归预测，提供了较多的选择余地，取得了较好的预测效果，但其针对的是平时作战需求。文献[6]基于兰彻斯特模型对战时的作战需求进行预测，模型充分考虑了作战效能对需求的影响。但上述模型均未考虑需求结构的影响。本文采用唯象型预测思想，通过对最近发生的战争进行研究，掌握航空弹药的作战需求规律，再搜集当前战争几个数据点，可对航空弹药作战需求总量进行预测。在需求总量预测的基础上，结合航空弹药作战的具体情况，建立需求结构模型，对主要作战因素、目标因素和炸弹自身因素进行定性和定量分析，得到航空弹药作战需求的最优结构，作为航空弹药需求的决策依据。

1 航空弹药作战需求总量预测模型

航空弹药是重要的压制火力，作战需求量极大，如果仅依据指挥员的历史经验进行预测，则存在很大偏差：预测总量过大，会带来巨大的经济负担；过小，则不能满足作战需求。

1.1 威布尔分布

威布尔分布在实际中有着广泛的应用，在航空弹药作战需求量预测和寿命估计中发挥着重要作用[7]。

三参数威布尔分布的概率分布特征函数[8-9]为

(1)概率密度函数

(1)

(2)分布函数

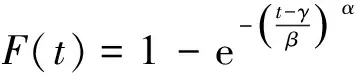
(2)

(3)数学期望

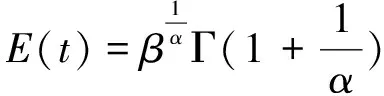
(3)

(4)数学方差

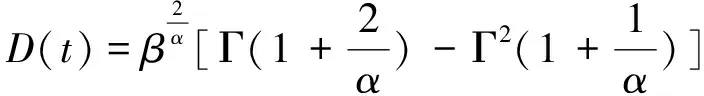
(4)

式中：α为形状参数，β为尺度参数，γ为位置参数，Γ(·)为伽玛函数。

各参数的取值情况同威布尔曲线的关系如下：

(1) 形状参数α决定着威布尔函数的形状。当α>1时，表现为单峰曲线；当α<1时，曲线随着t的变化而单调递减，而且它以t=γ为渐近线，α越小，曲线越趋近于直线t=γ；当α=1时，表现为指数曲线；当α>3时，和正态分布曲线很接近。如图1所示。

(2) 尺度参数β决定曲线的陡峭程度。

(3) 位置参数γ反映曲线的起始位置情况，当γ=0时，模型退化为二参数威布尔模型。

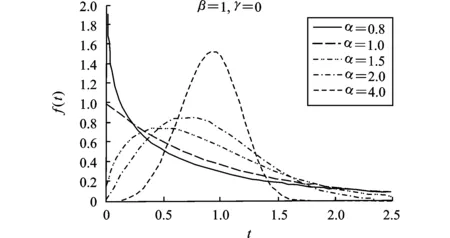
图1 威布尔分布密度曲线

1.2 航空弹药作战需求量预测

战斗过程划分为开始、中间和结束3个阶段，如果战斗不出现大的突变性，那么航空弹药的需求量具备如下特点：开始和结束少，中间多，并且开始和结束阶段需求量的变化较为平缓，随着战斗的全面展开，中间阶段的需求量急剧增加(反映了战斗的激烈程度)。根据对海湾战争(1990年)和伊拉克战争(2003年)数据的掌握情况，绘制出美军的航空弹药消耗规律分别如图2、图3所示。图2出现两个波峰，是因为在海湾战争中期进行了“沙漠风暴”和“沙漠之狐”两次行动[10]。

图2 海湾战争航空弹药消耗

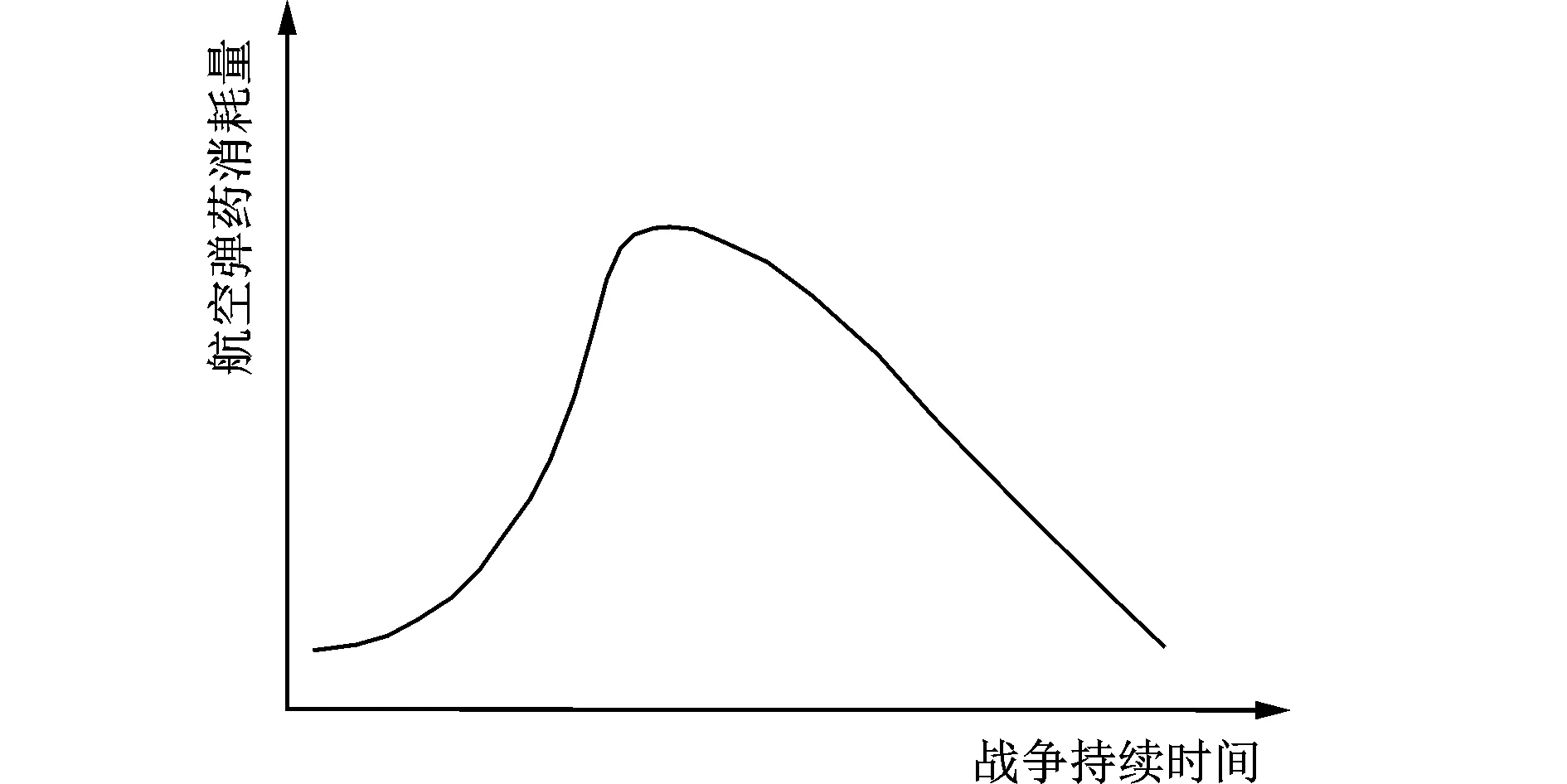
图3 伊拉克战争航空弹药消耗

假定航空弹药的作战需求量服从威布尔分布，则航空弹药作战需求量预测的关键是威布尔分布参数的确定。本文采用矩估计法对威布尔分布的参数进行估计。

矩估计法的基本思想是用子样的各阶矩(或中心矩)估计母体的各阶矩(或中心矩)。由于战争初期就存在航空弹药消耗，因此位置参数γ=0，此时航空弹药作战需求量的分布变为二参数威布尔分布。为使问题简化便于求解，进行如下假设：

(1)航空弹药作战需求量是一次作战或战役中的需求量；

(2)航空弹药作战需求量属于独立分布，且符合某一分布；

(3)航空弹药的作战需求量是一个客观过程，排除人为决策影响；

(4)航空弹药的作战需求量为所有种类航空弹药的需求总量，对需求数据进行归一化处理。

根据矩估计法求解模型参数的基本思想：用子样均值去估计母体的数学期望，用子样方差去估计母体的方差，即可求得二参数威布尔分布的参数。

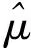
(5)

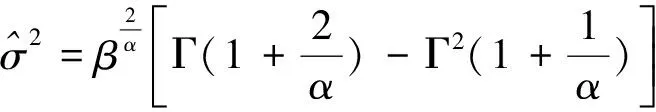
(6)

将式(5)平方后，与式(6)相除，可得

(7)

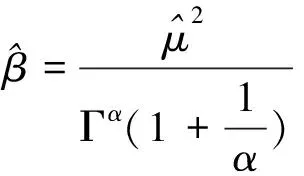
(8)

从而可估计参数α和β的值，代入式(1)即可求得航空弹药作战需求量的变化规律，利用海湾战争的航空弹药需求数据对模型进行检验，当置信水平达到90%时，同实际的符合程度极好。

威布尔分布参数估计应用比较成熟的方法还有：威布尔概率纸法、极大似然估计法和最小二乘法。比较新的方法有：最好线性无偏估计(Best linnear uniased estimation，BLUE)、简单线性无偏估计(GLUE)、概率权重法、相关系数优化法和灰色估计法等[8-9]。

1.3 实例分析

通过对空军演习中航空弹药需求量历史数据的收集和整理，获得数据如表1所示[7，10]。

表1 航空弹药作战需求量

为使量纲统一，对其进行归一化处理，处理后的数据如表2所示。

表2 归一化后的作战需求量数据

根据所给方法进行参数估计：α=2.31，β=44.9。

航空弹药作战需求量的概率密度函数为

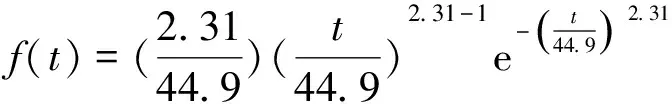
(9)

航空弹药需求量变化曲线，如图4所示。

考虑到航空弹药演习中需求量与威布尔分布量纲的统一，将威布尔曲线与归一化之后的数据进行对照，对照结果如图4所示，可发现当置信水平为0.9时，预测值与实际数据拟合程度很好，达到预测要求。

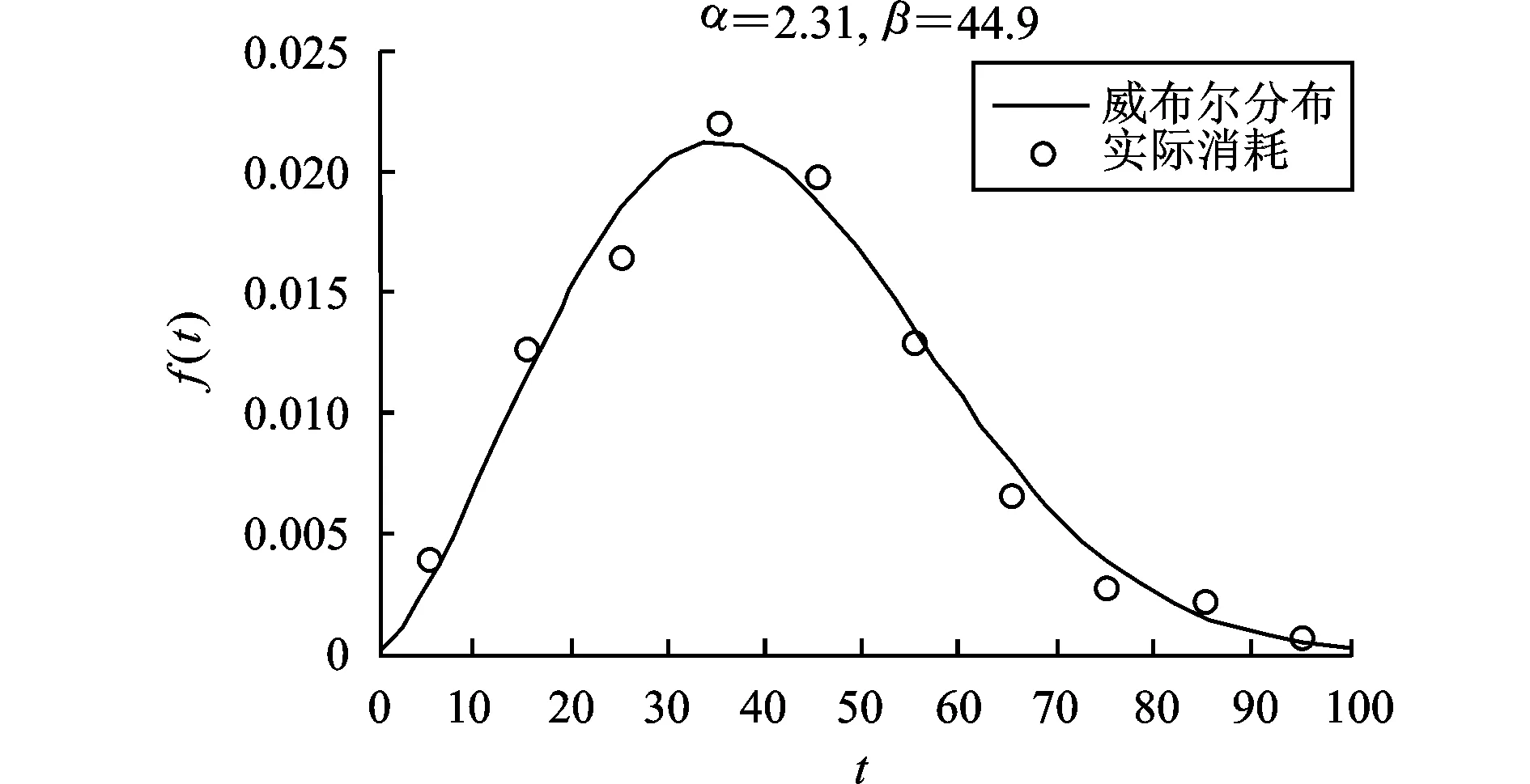
图4 模型结果与实际需求对比

2 航空弹药作战需求结构模型

在整个海湾战争期间，美军共投掷8.42 万t航空弹药，但其中7 400 t为精确制导弹药，仅占到投弹量的9%，常规弹药比例达到91%，占据绝大部分比例[11-12]。什么样的比例结构才是最合理、如何确定航空弹药的需求结构是本文研究的重点。

2.1 问题的提出

航空弹药作战需求结构问题可归结为：已知威胁敌的种类及威胁程度，每个威胁敌拥有的关键目标的重要程度及数量，并且知道己方的航空弹药种类、单价以及毁伤敌方各种关键目标所需的每种航空弹药数，据此求航空弹药的作战需求结构，以获得最佳的军事和经济效益。

2.2 层次分析法

层次分析法由于在处理复杂的决策问题上的实用性和有效性，很快就在世界范围内得到普遍重视和广泛应用。

(1)层次分析流程

经过理论研究和实际工程应用，利用层次分析法建模已形成鲜明的固定流程。层次分析法建模的流程如图5所示。

(2)层次分析步骤

步骤1：分析系统中各要素的关系，建立递阶层次结构模型，一个典型的层次结构模型如图6所示。

步骤2：根据上一层次中的某一因素对于本层中所有元素的影响，进行相对重要性的成对比较，构造判断矩阵A。

步骤3：求解判断矩阵的最大特征值及特征向量，并进行归一化处理，求得权向量。并进行一致性检验。

步骤4：计算同层次所有因素对最高层的相对权重值，并计算总排序的随机一致性比率CR。通常，当CR<0.1时，认为层次总排序结果具有满意的一致性，否则还需要重新调整比较矩阵的元素取值。

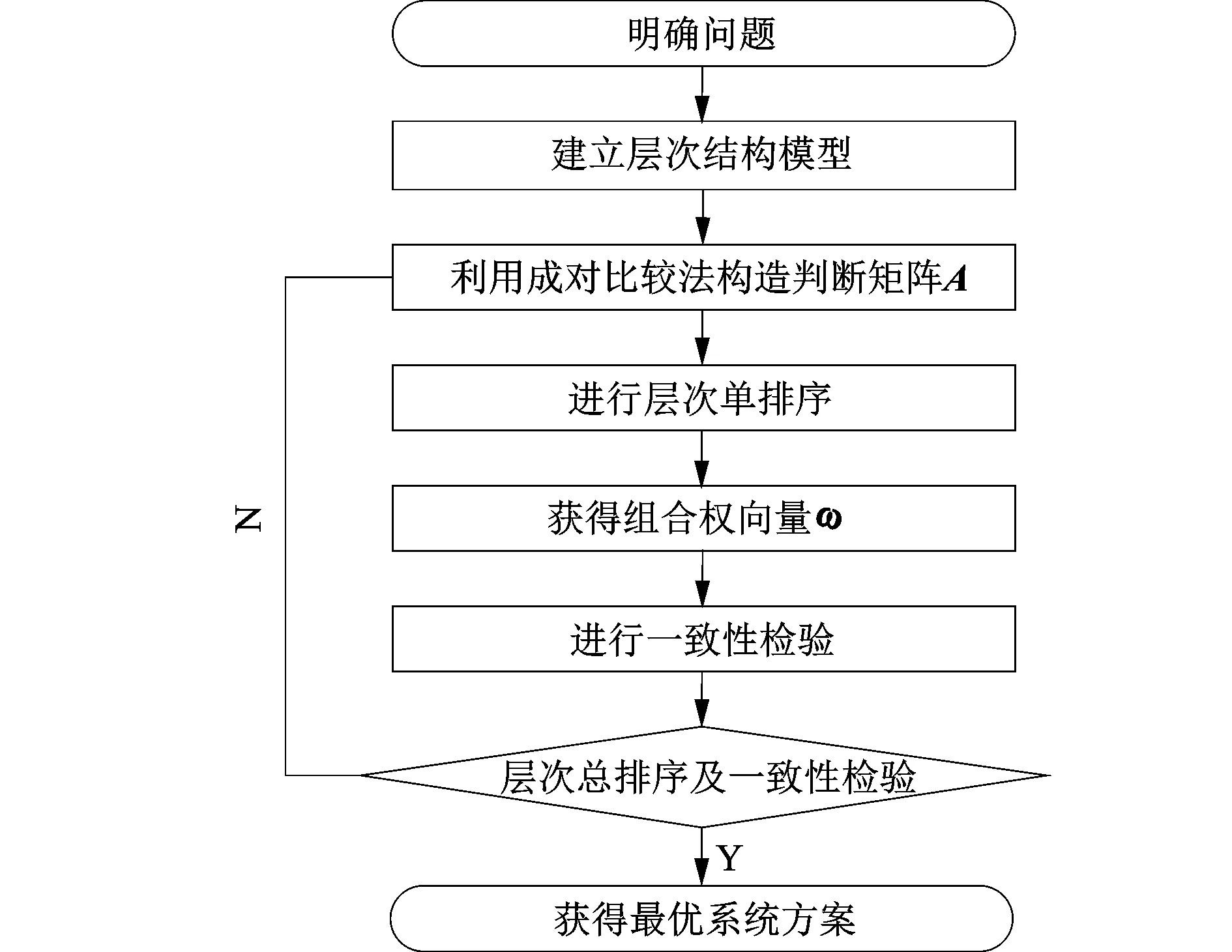
图5 层次分析法建模流程图

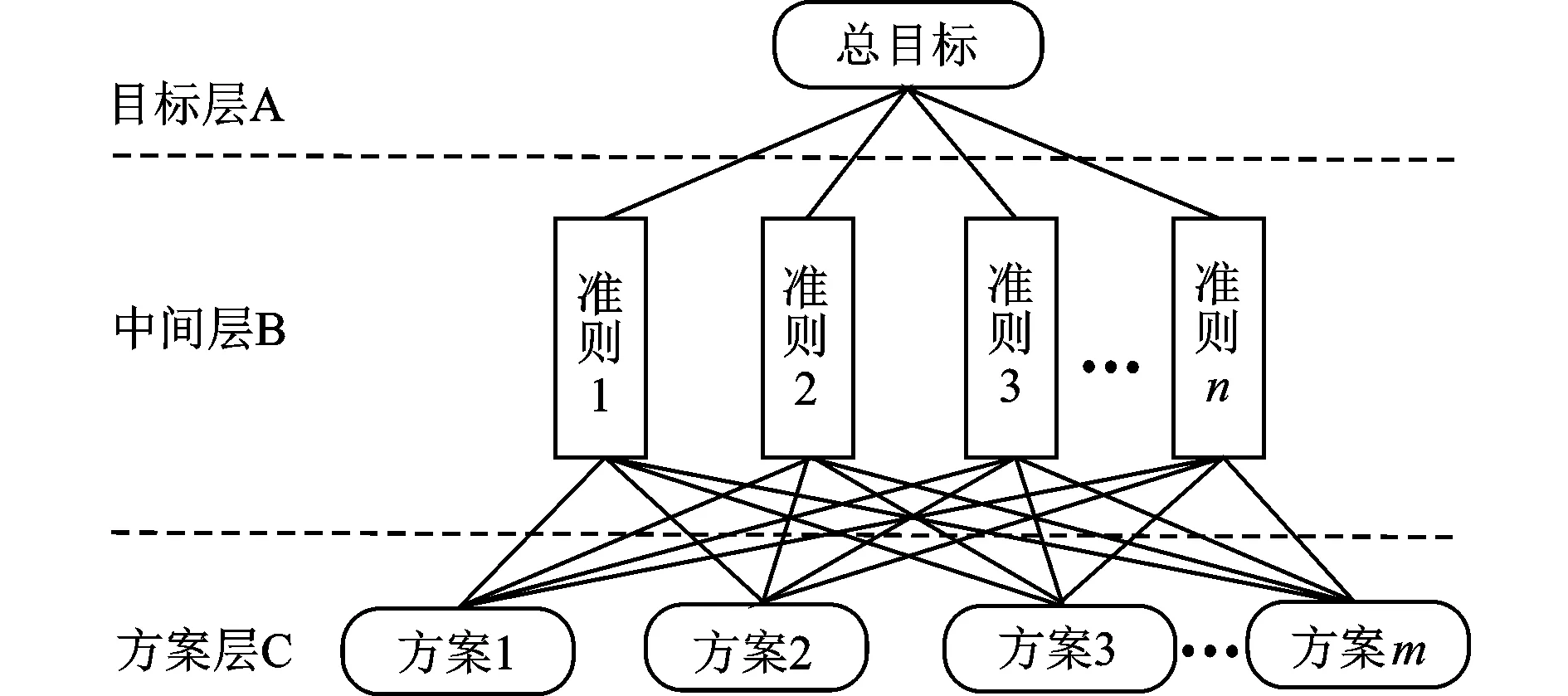
图6 层次结构模型示意图

2.3 航空弹药需求结构模型

航空弹药种类繁多，依据作战飞机类型及挂载能力确定航空弹药需求结构的方法偏差较大，不够合理。采用层次分析法，结合航空弹药的具体情况，对主要作战因素、目标因素及炸弹自身因素进行定性和定量分析，得出的航空弹药需求结构具有一定的科学指导意义。

(1)模型建立

在航空弹药需求结构模型中，既有定性因素，又有定量因素，采用层次分析法建立航空弹药需求结构模型，可以很好地将定性因素与定量因素结合起来，给出科学的需求结构。

建立航空弹药需求结构的层次分析模型如图7所示，模型共分4层：目标层是航空弹药需求优先系数，它决定了需求结构；准则层分准则层1和准则层2，准则层1反映存在的威胁敌，准则层2反映各威胁敌的关键目标情况；方案层是航空弹药的种类，主要考虑各型航空弹药突击单一关键目标所需数量和价格。

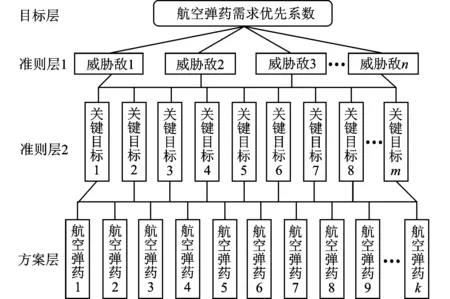
图7 航空弹药需求结构层次模型

(2)模型求解

步骤1：构造成对比较矩阵

假定己方当前存在威胁敌1、威胁敌2、…、威胁敌n，根据其对己方的威胁程度及威胁能力，通过专家评价构造准则层1对目标层的成对比较矩阵An×n

(10)

根据准则层1中的各威胁敌包含的关键目标的重要程度及数量，通过专家评价构造准则层2对准则层1的成对比较矩阵B1、B2、…、Bl、…、Bn。其中

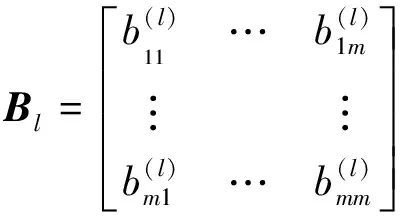
(11)

根据方案层中各种航空弹药毁伤关键目标的数量及价格，构造方案层对准则层2的成对比较矩阵C1、C2、…、Cl、…、Cm。其中

(12)

步骤2：计算权向量并做一致性检验

对于每一个成对比较矩阵，求取最大特征根及其对应的特征向量，利用一致性指标和一致性比率做一致性检验。若检验通过，特征向量(归一化后)即为权向量；否则，需要对未通过检验的成对比较矩阵进行改进使其通过一致性检验。

步骤3：计算组合权向量并做组合一致性检验

分别计算准则层2和方案层对目标层的组合权向量，计算方法如下

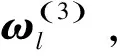
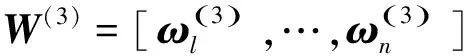
(13)

记准则层1中成对比较矩阵An×n满足一致性检验的权向量为ω(2)，则准则层2对目标层的组合权向量为

ω(3)=W(3)ω(2)

(14)

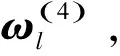
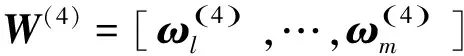
(15)

则方案层对目标层的组合权向量为

ω(4)=W(4)ω(3)

(16)

进行组合一致性检验，检验方法如下

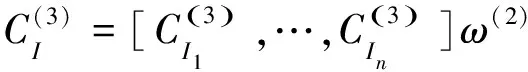
(17)

(18)

则准则层2的组合一致性比率为

(19)

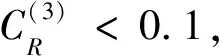
2.4 实例分析

设当前存在两个威胁敌，定义10种关键目标，装备4种航空弹药，构建如图8所示航空弹药需求结构模型。

图8 航空弹药需求结构层次分析模型

邀请专家就图8中的层次分析模型中各因素进行比较分析，构造每层的判断矩阵。其中，A阵表示准则层1中各威胁敌的威胁程度比较

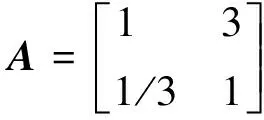
(20)

B1(B2)阵表示各关键目标对威胁敌A(B)的重要程度及规模的综合比较

(21)

(22)

Cl阵表示每种航空弹药对关键目标Cl进行突击所需的数量及价格的综合比较

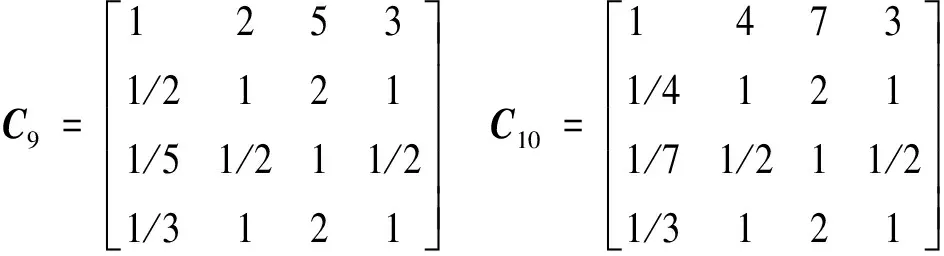
(23)

采用Matlab提供的EIG函数，求得各判断矩阵的最大特征根及特征向量，通过归一化处理求得权向量，并进行一致性检验。

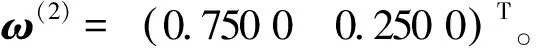
根据准则层2的B1阵可以求得

(24)

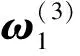
根据准则层2的B2阵可以求得

(25)

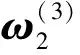
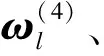
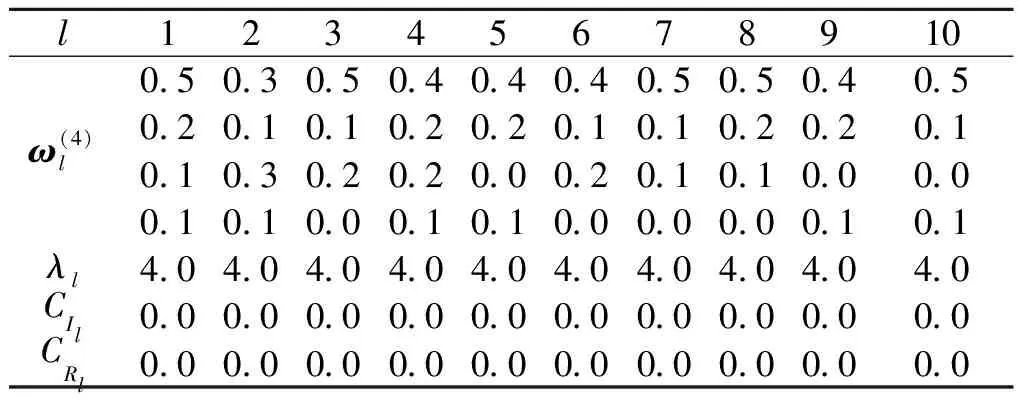
表3 方案层的计算结果

根据式(13～16)，可求得准则层2、方案层对目标层的组合权向量分别为

(26)

ω(4)= ( 0.589 6,0.236 8,0.219 1,0.161 3)T

(27)

组合一致性检验：因为准则层1的判断矩阵为2阶，所以，准则层2对准则层1的一致性检验通过，从而，准则层2的组合一致性检验通过。

根据式(17～19)求得

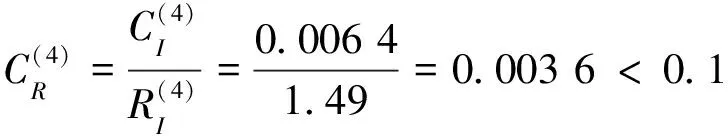
(28)

因此组合一致性检验通过，ω(4)可以作为航空弹药作战需求结构的依据。即在航空弹药的需求结构中，A、B、C、D四型航空弹药需求量的最佳比例为：0.589 6∶0.236 8∶0.219 1∶0.161 3。

3 结论

本文构建了航空弹药的作战需求总量预测模型及结构模型。通过分析最近两次高技术局部战争中航空弹药消耗的特点，得出航空弹药需求量的威布尔分布模型，并通过算例对模型进行检验。在预测需求总量的基础上，结合航空弹药作战的具体情况，建立层次分析结构模型，对主要作战因素、目标因素和炸弹因素进行定性和定量分析，得出航空弹药需求的最优结构。